Gradient Accumulation (梯度累积 / 梯度累加) in PyTorch

Gradient Accumulation {梯度累积 / 梯度累加} in PyTorch

[1. Gradient accumulation improves memory efficiency](#1. Gradient accumulation improves memory efficiency)
[2. Gradient accumulation with PyTorch](#2. Gradient accumulation with PyTorch)
[3. Gradient accumulation with Accelerator](#3. Gradient accumulation with Accelerator)
[4. Gradient accumulation with Trainer](#4. Gradient accumulation with Trainer)
References

Gradient accumulation, Gradient checkpointing and local SGD, Mixed precision training
https://projector-video-pdf-converter.datacamp.com/37998/chapter3.pdf

Improving training efficiency

1. Gradient accumulation improves memory efficiency

https://www.mindspore.cn/tutorials/experts/zh-CN/r2.3.1/optimize/gradient_accumulation.html

梯度累加是将训练神经网络的数据样本按 Batch Size 拆分为多个 Mini-Batch，然后按顺序进行计算。将多次计算得到的梯度值进行累加，然后一次性进行参数更新。梯度累加是利用时间换空间的优化方法。

在神经网络层中，样本数据会不断向前传播。在通过所有层后，网络模型会输出样本的预测值，通过损失函数然后计算每个样本的损失值 (误差)。神经网络通过反向传播，去计算损失值相对于模型参数的梯度。最后这些梯度信息用于对神经网络模型中的参数进行更新。

假设 Loss Function 公式：

L o s s ( θ ) = 1 2 ( h ( x k ) − y k ) 2 Loss(\theta)=\frac{1}{2}\left(h(x^{k})-y^{k}\right)^{2} Loss(θ)=21(h(xk)−yk)2

随机梯度下降 (SGD) 算法根据优化器来更新神经网络模型权重参数：

θ i = θ i − 1 − l r ∗ g r a d i \theta_{i}=\theta_{i-1}-lr * grad_{i} θi=θi−1−lr∗gradi

其中 θ \theta θ 是网络模型中的可训练参数 (权重或偏差)， l r lr lr 是学习率， g r a d i grad_{i} gradi 是相对于网络模型参数的损失。

梯度累加计算神经网络模型，并不及时更新网络模型的参数，在计算的时候累加得到的梯度信息，最后统一使用累加的梯度来对参数进行更新。

a c c u m u l a t e d = ∑ i = 0 N g r a d i accumulated=\sum_{i=0}^{N} grad_{i} accumulated=i=0∑Ngradi

在 N 个 step 内不更新变量，使所有 Mini-Batch 使用相同的模型变量来计算梯度，以确保计算出来得到相同的梯度和权重信息，算法上等价于使用原来没有切分的 Batch Size 大小一样。

θ i = θ i − 1 − l r ∗ ∑ i = 0 N g r a d i \theta_{i}=\theta_{i-1}-lr * \sum_{i=0}^{N} grad_{i} θi=θi−1−lr∗i=0∑Ngradi

最终在上面步骤中累加梯度会产生与使用全局 Batch Size 大小相同的梯度总和。

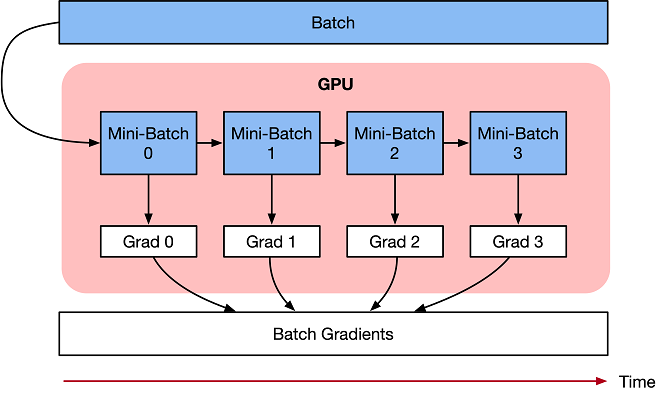
在实际工程中，需要注意：

Learning Rate：一定条件下，Batch Size 越大训练效果越好，梯度累加则模拟了 Batch Size 增大的效果。如果 Accumulation Steps 为 4，则 Batch Size 增大了 4 倍。根据经验，使用梯度累加的时候需要把学习率适当放大。
Batch Norm：Accumulation Steps 为 4 时进行 Batch Size 模拟放大的效果，与真实 Batch Size 相比，数据的分布其实并不完全相同，4 倍 Batch Size 的 Batch Norm 计算出来的均值和方差与实际数据均值和方差不太相同，因此有些实现中会使用 Group Norm 来代替 Batch Norm。

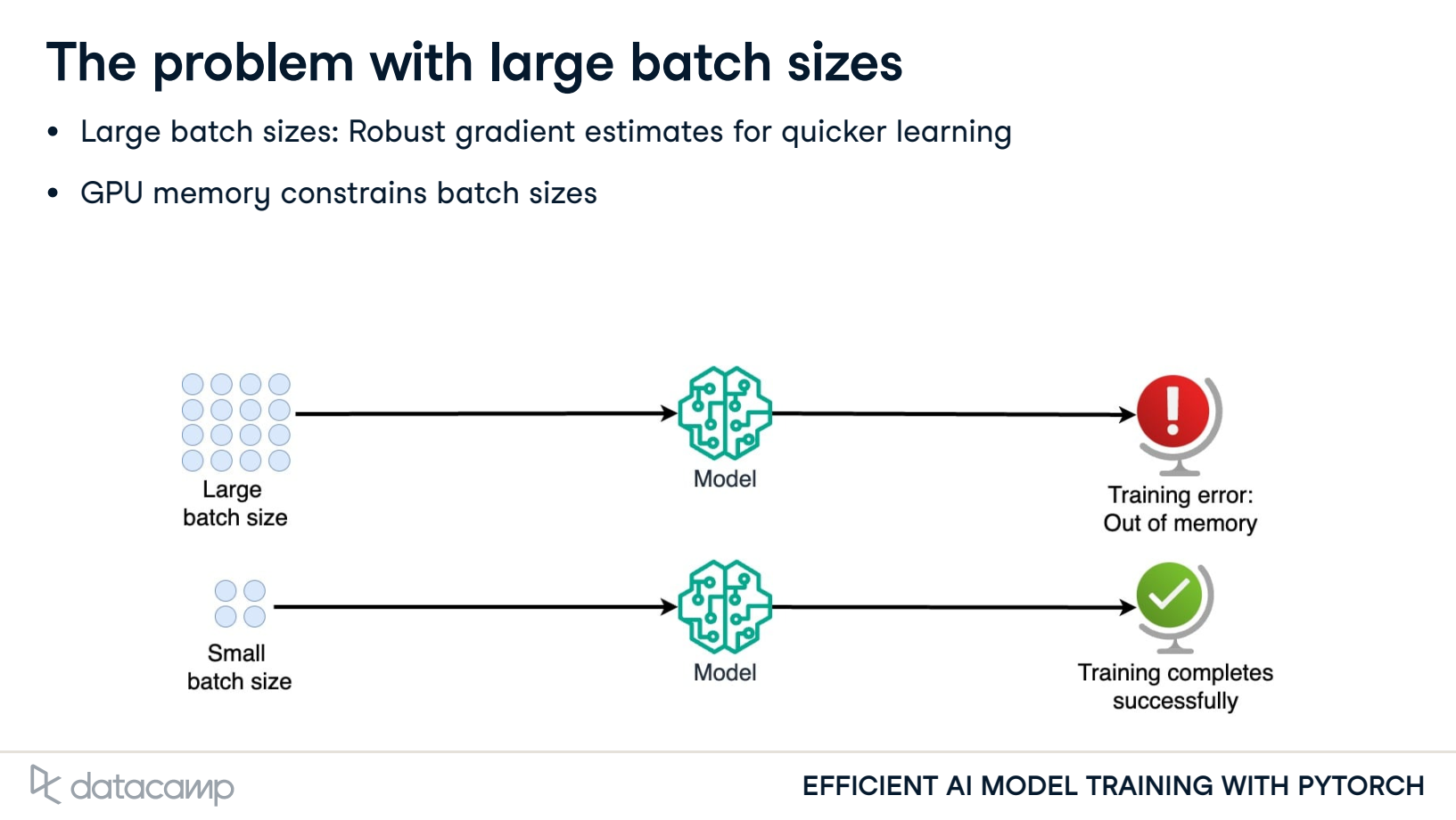
The problem with large batch sizes

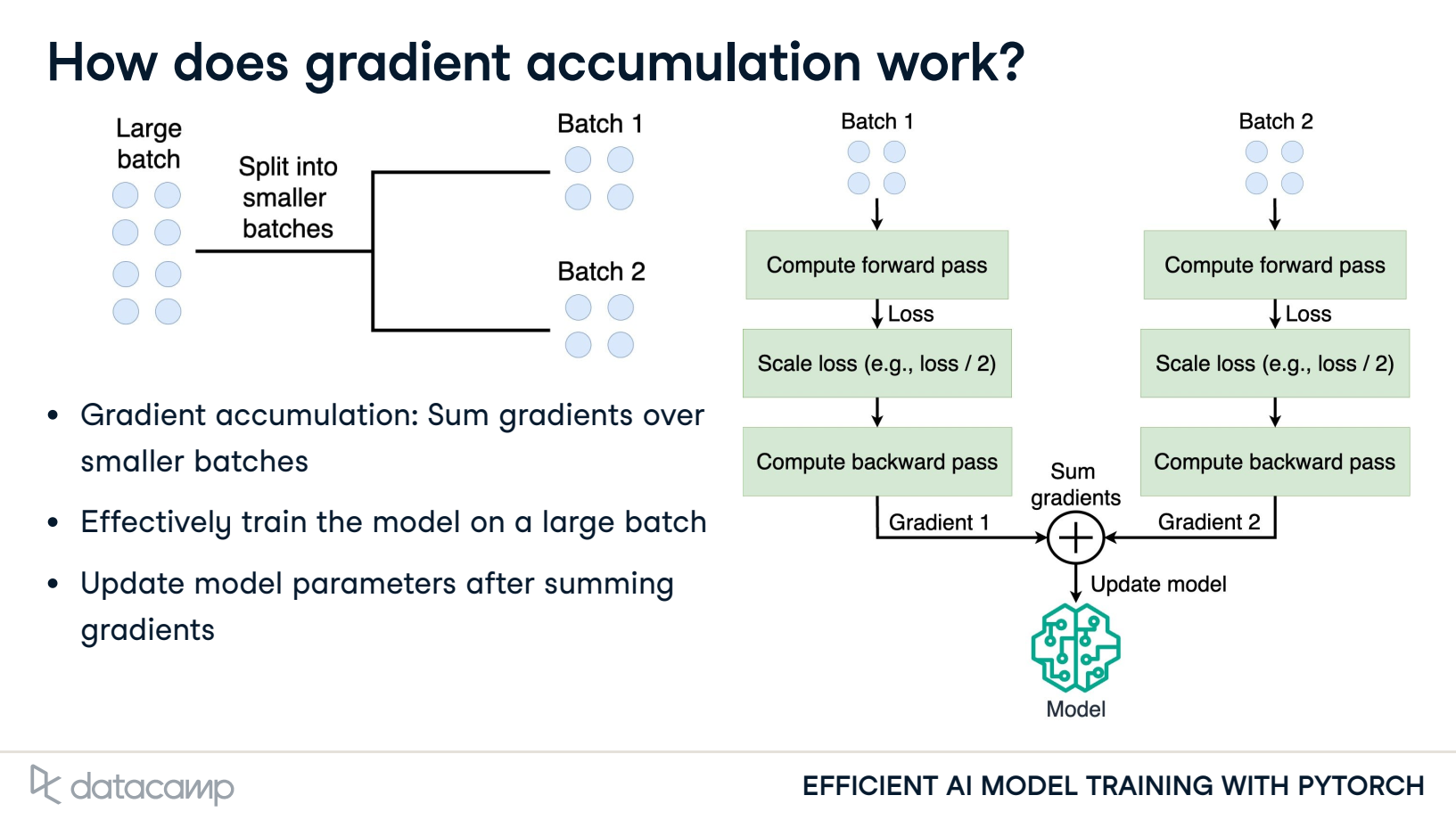
How does gradient accumulation work?

Gradient accumulation: Sum gradients over smaller batches
Update model parameters after summing gradients

From PyTorch to Accelerator

2. Gradient accumulation with PyTorch

Without Gradient Accumulation (梯度累积)

optimizer = ...

for epoch in range(...):
for i, sample in enumerate(dataloader):
inputs, labels = sample

复制代码

      # Forward Pass
      outputs = model(inputs)
      # Compute Loss and Perform Back-propagation
      loss = loss_fn(outputs, labels)
      loss.backward()
      # Update Optimizer
      optimizer.step()

      optimizer.zero_grad()

With Gradient Accumulation (梯度累积)

optimizer = ...
NUM_ACCUMULATION_STEPS = ...

for epoch in range(...):
for idx, sample in enumerate(dataloader):
inputs, labels = sample

复制代码

      # Forward Pass
      outputs = model(inputs)
      # Compute Loss and Perform Back-propagation
      loss = loss_fn(outputs, labels)

      # Normalize the Gradients
      loss = loss / NUM_ACCUMULATION_STEPS
      loss.backward()

      if ((idx + 1) % NUM_ACCUMULATION_STEPS == 0) or (idx + 1 == len(dataloader)):
              # Update Optimizer
              optimizer.step()

              optimizer.zero_grad()

梯度累加的核心思想是将多个 Mini-Batch 的梯度相加，然后使用累加的梯度来更新模型参数。

选择 Mini-Batch 大小：Mini-Batch 大小的数据是每一次正反向传播的基本批次，同时根据 Batch 除以 Mini-Batch 得到累加步数，可以确定在多少个 Mini-Batch 之后进行一次参数更新。
前向传播和反向传播：对于每个 Mini-Batch，执行标准的前向传播和反向传播操作，计算小批次的梯度。
梯度累加：将每个 Mini-Batch 的梯度值相加，直到达到累加步数。
梯度更新：在达到累加步数后，使用累加的梯度来通过优化器更新模型参数。
梯度清零：在梯度更新后，将梯度值清零，以便下一个累加周期的计算。

3. Gradient accumulation with Accelerator

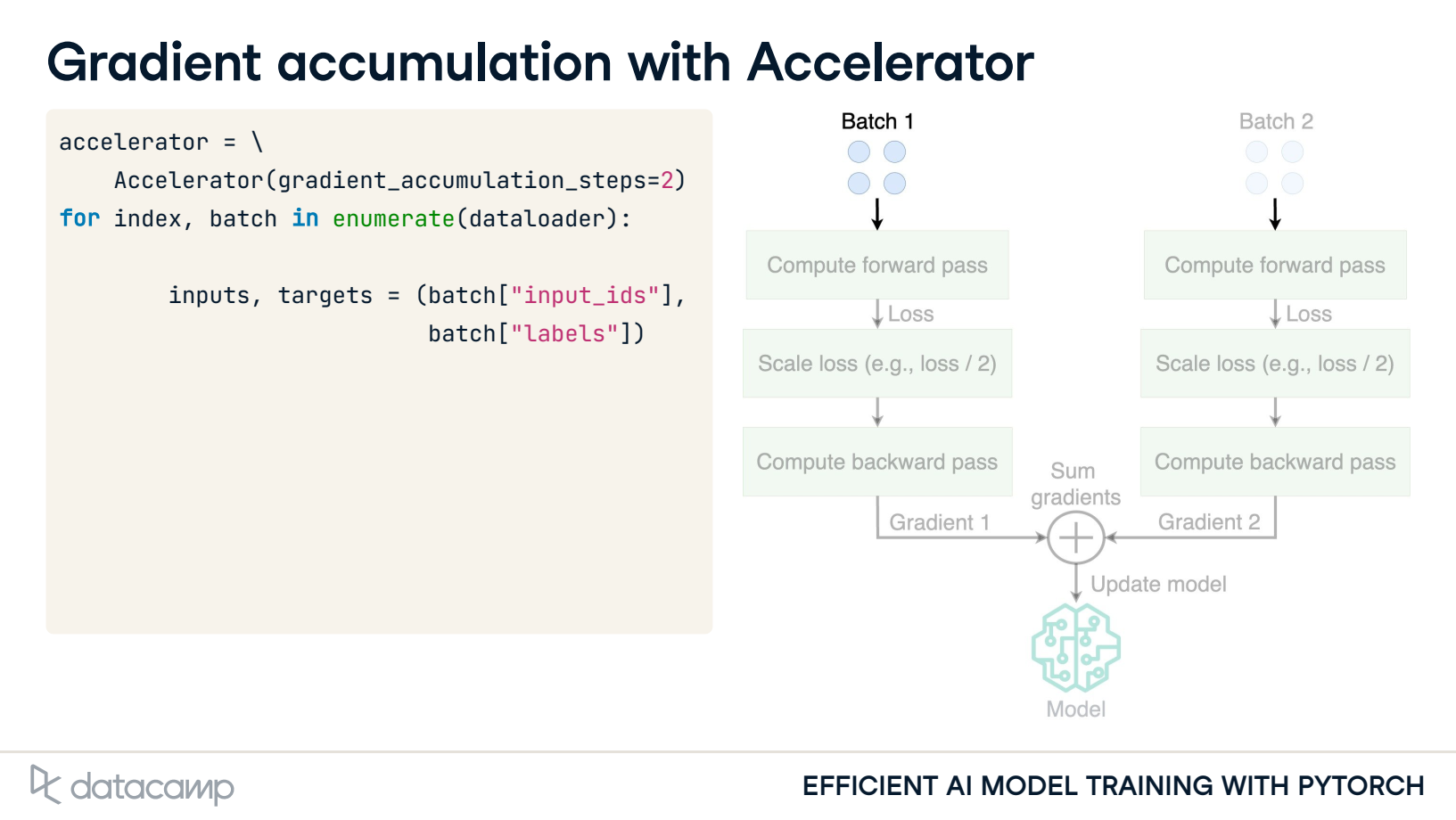
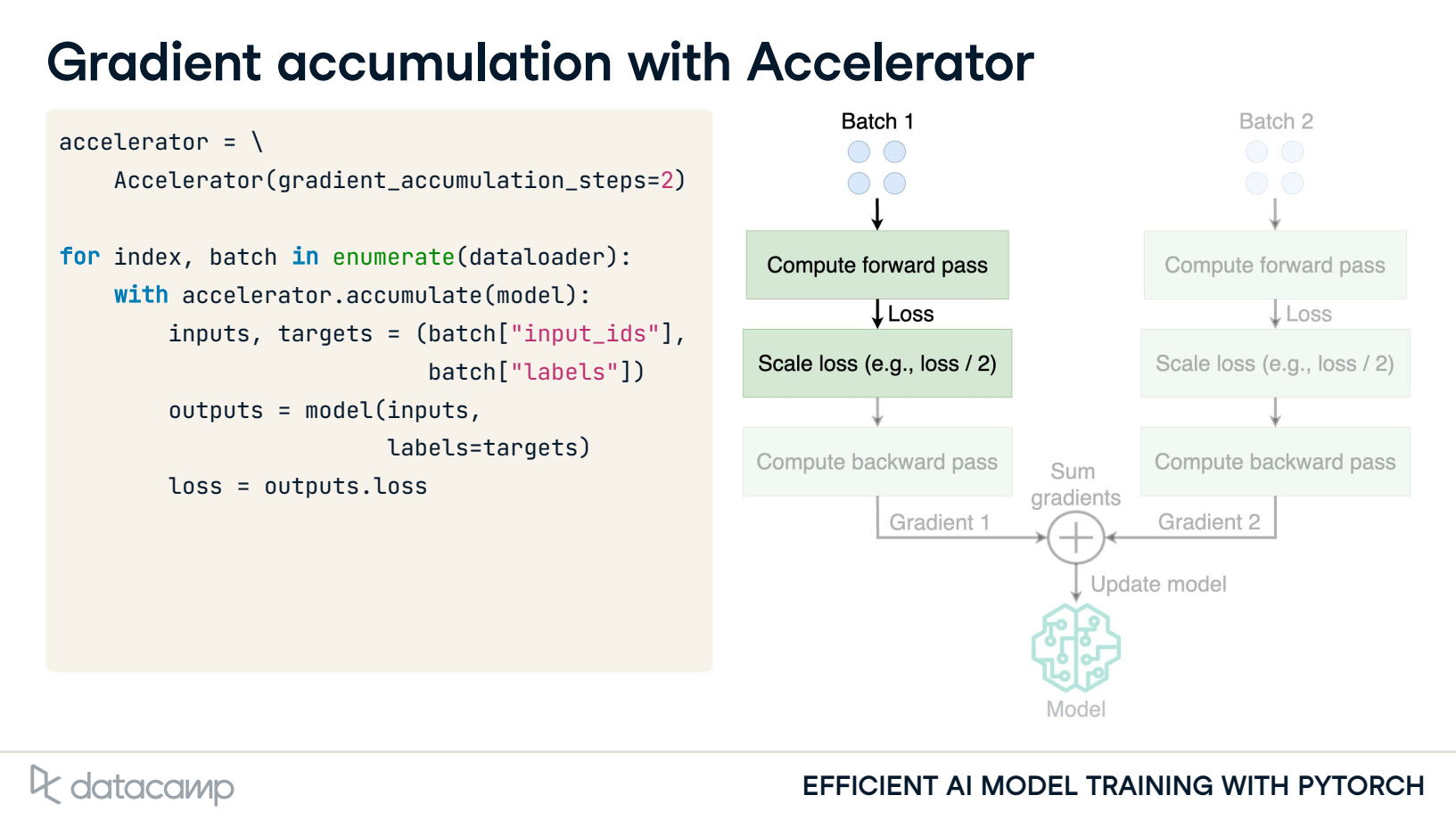
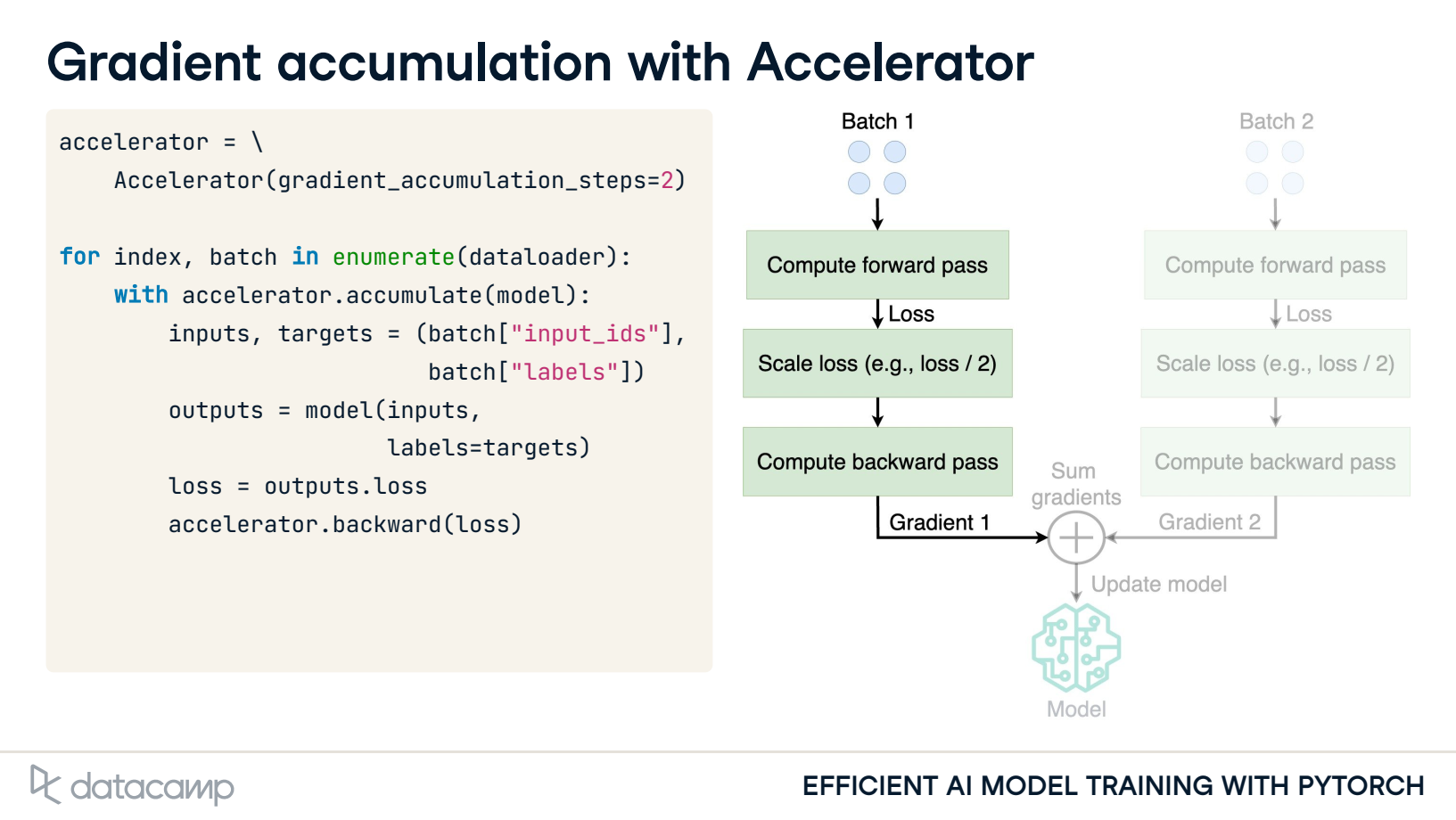
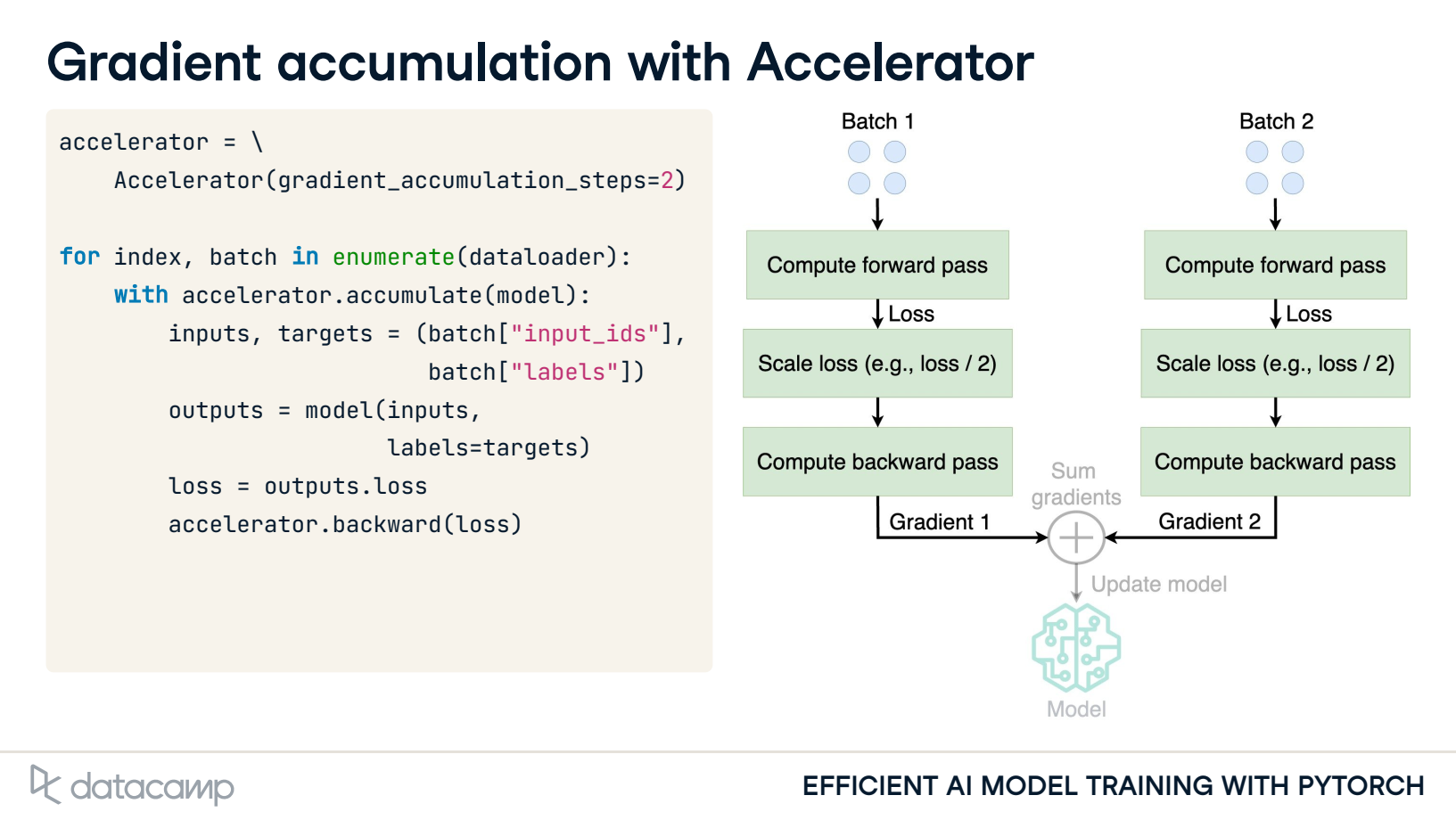
4. Gradient accumulation with Trainer

References

1\] Yongqiang Cheng (程永强), \[2\] Gradient accumulation, Gradient checkpointing and local SGD, Mixed precision training,