文章目录
- 一、说明
- 二、什么是几何分布?
- 三、理解几何分布
- 四、累积概率和分布函数
- [五、 绘制几何分布图](#五、 绘制几何分布图)
- 六、创建您自己的几何分布可视化
- 七、几何分布的无记忆性
-
- [7.1 无记忆特性](#7.1 无记忆特性)
- [7.2 与伯努利试验和实验的关系](#7.2 与伯努利试验和实验的关系)
- [7.3 与连续模拟物形成对比](#7.3 与连续模拟物形成对比)
一、说明
本指南涵盖几何分布的数学基础、独特性质及其在实际应用中的价值,尤其适用于处理序贯试验场景的人员。如需复习概率分布,建议参加我们的统计学入门课程。
二、什么是几何分布?
几何分布是一种离散概率分布,它模拟了达到首次成功所需的独立伯努利试验次数。每次试验成功的概率相同,且各次试验彼此独立。
这种分布有两种常见形式:一种是计算直到第一次成功(包括成功本身)的总试验次数,另一种是只计算第一次成功之前的失败次数。根据具体应用场景,这两种形式都有广泛的应用。在本指南中,我们将使用第一种形式,即计算直到第一次成功的总试验次数,其中 X 可以取值 1、2、3 等等。
三、理解几何分布
让我们来研究定义该分布的数学结构和特征。
基本定义和概率结构
几何分布需要三个关键条件:独立试验、所有试验中成功的概率相同,以及固定的概率 p,其中 0 < p ≤ 1。标准符号用 p 表示成功的概率,用 q = 1-p 表示失败的概率。
首次成功前所需试验次数 X 的概率质量函数 (PMF) 为:
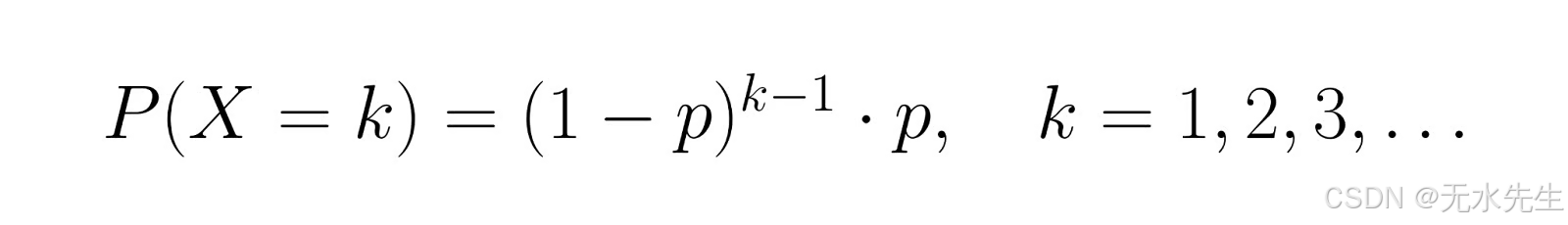
该公式计算经历 k-1 次失败后成功一次的概率。例如,如果 p = 0.3,则第三次试验成功的概率为 P(X = 3) = (0.7)² × 0.3 = 0.147。
四、累积概率和分布函数
累积分布函数(CDF)告诉我们:
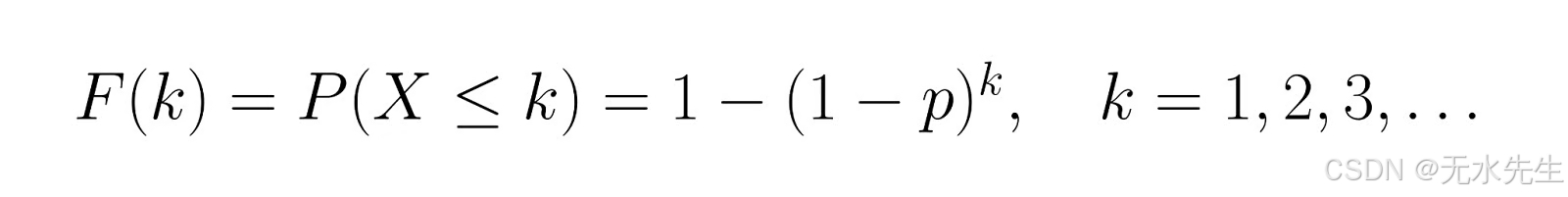
这表示在 k 次试验中获得成功的概率。以 p = 0.3 为例,我们来计算前几个值的累积分布函数 (CDF):
• F(1) = P(X ≤ 1) = 1 - (0.7)¹ = 0.3
• F(2) = P(X ≤ 2) = 1 - (0.7)² = 1 - 0.49 = 0.51
• F(3) = P(X ≤ 3) = 1 - (0.7)³ = 1 - 0.343 = 0.657
这表明第一次试验成功的概率为 30%,前两次试验成功的概率为 51%,前三次试验成功的概率为 65.7%。
五、 绘制几何分布图
几何分布的视觉模式揭示了"等待时间"场景的关键信息。这些图表展示了概率如何在早期试验中集中,并呈指数级下降,因此该分布适用于模拟成功概率较高的情况。
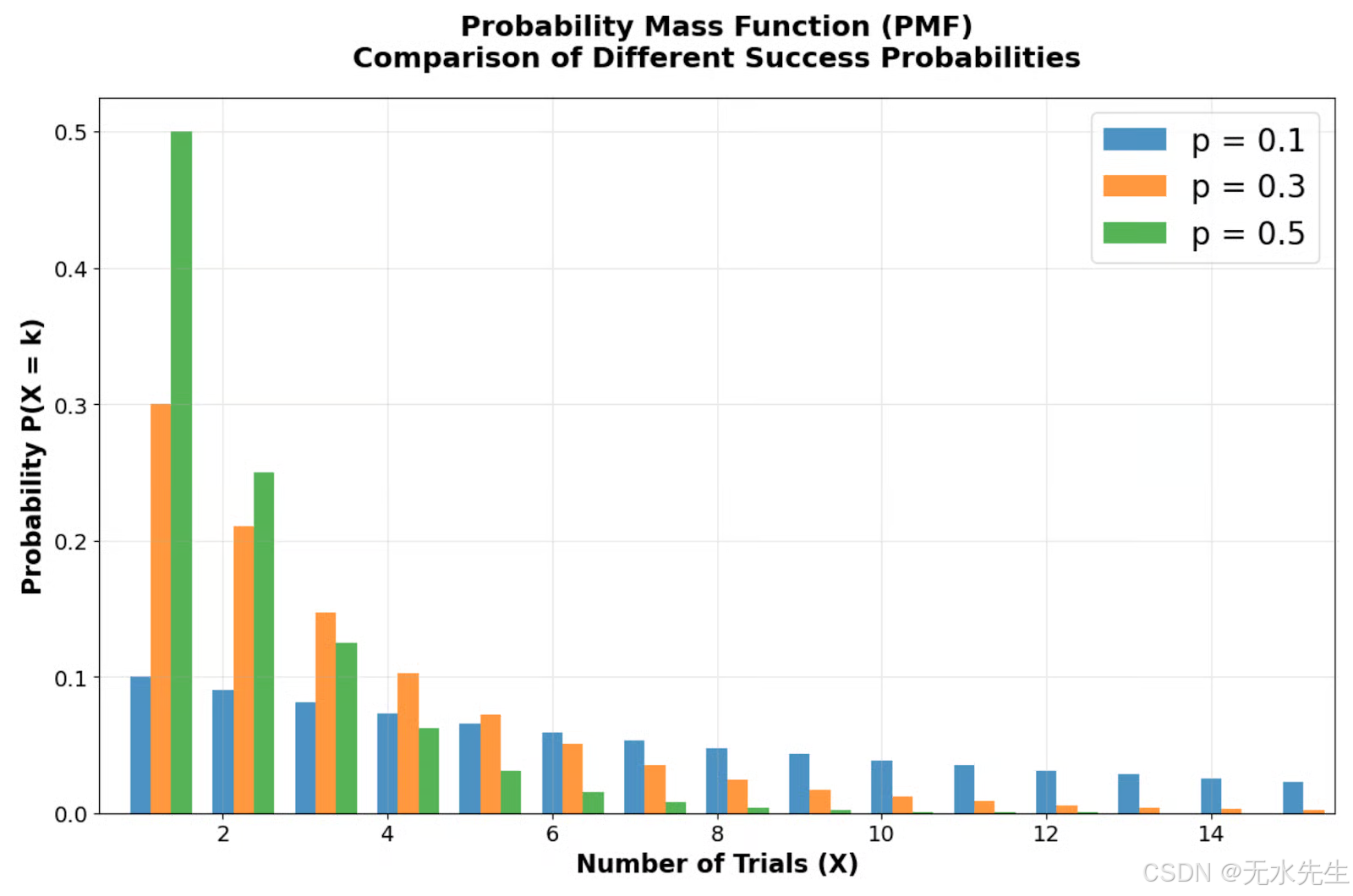
概率质量函数对比图,展示了不同成功概率(p = 0.1、0.3、0.5)如何影响分布形状。
通过比较不同成功概率下的概率密度函数,可以看到几何分布呈现出独特的右偏形状,其众数始终位于 X = 1(第一次试验)。注意概率柱状图在第一次试验时最高,之后每次试验呈几何级数下降。随着成功概率 p 的降低,分布变得更加分散,反映出预期等待时间的延长。例如,当 p = 0.1 时,立即成功的概率仅为 10%,与 p = 0.5 相比,其分布的右尾更加明显。
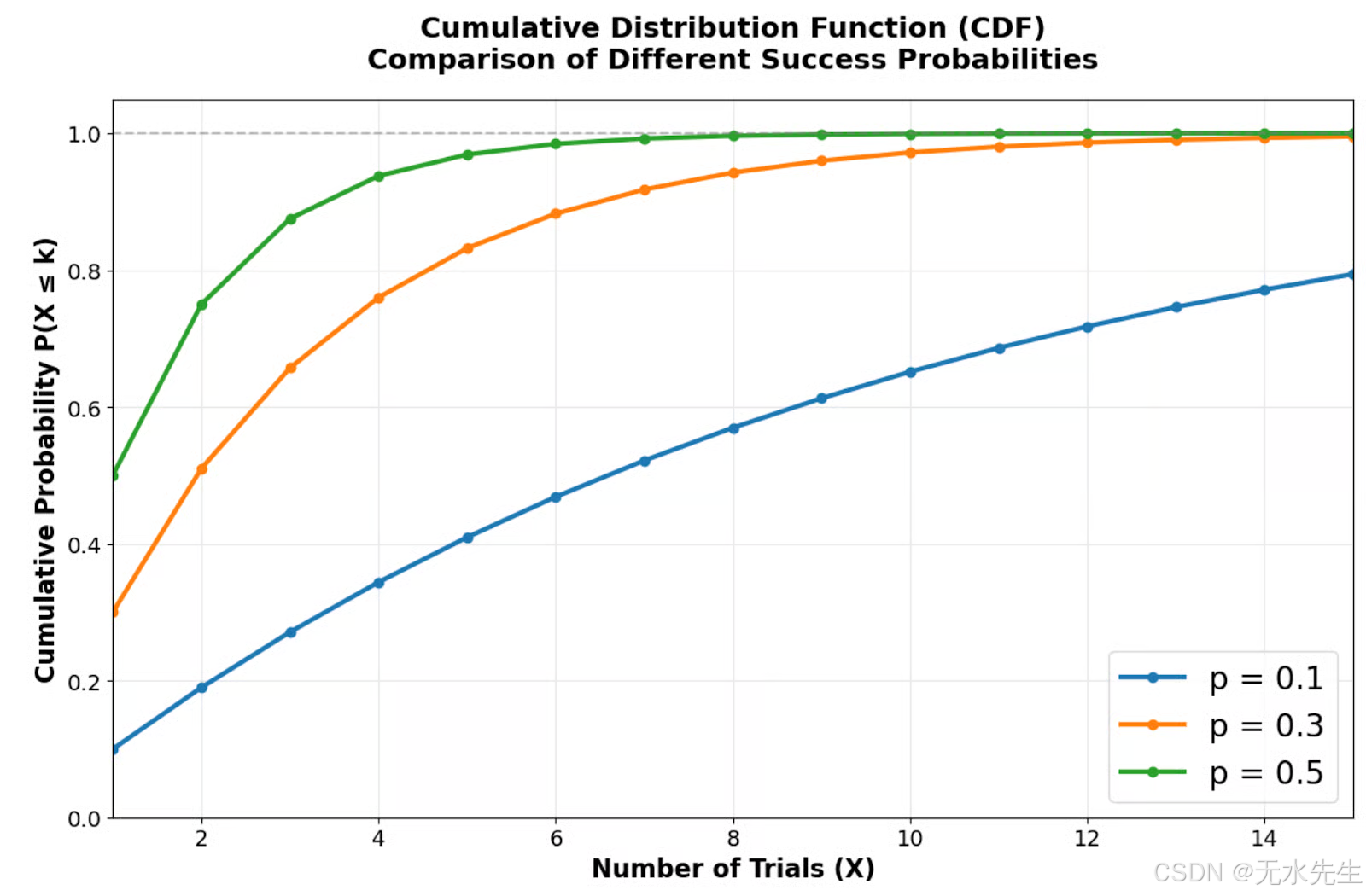
斜体样式累积分布函数展示了不同成功概率趋近于确定性的速度。
累积分布函数展示了几何分布趋近于确定性的速度。较高的成功概率会产生更陡峭的曲线,只需几次试验即可达到较高的累积概率。例如,当 p = 0.5 时,前两次试验的成功概率约为 75%;而当 p = 0.1 时,则需要更多的试验才能达到相同的确定性水平。
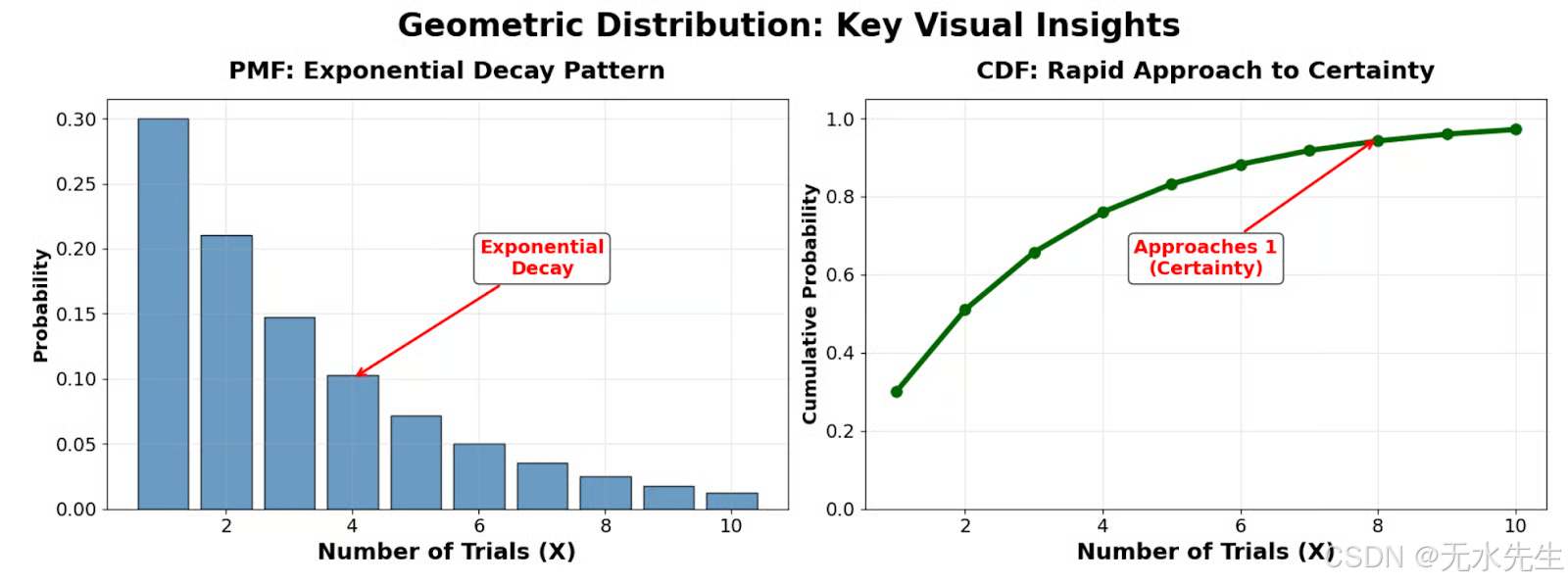
并排比较突显了PMF的指数衰减模式和CDF快速趋于确定性的特点。
这种指数衰减模式解释了为什么几何分布适用于模拟早期成功比长时间等待更有可能发生的场景。累积分布函数 (CDF) 快速趋近于 1 表明,这种分布适用于模拟等待时间较短的过程,使其在质量控制、客户转化分析和可靠性测试等场景中具有重要价值。
六、创建您自己的几何分布可视化
您可以使用 Python 的 scipy 和 matplotlib 库来重现这些可视化效果,并探索不同的参数值。以下是如何生成关键的视觉洞察,以突出几何分布最重要的特征:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# Create side-by-side plots for PMF and CDF
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('Geometric Distribution: Key Visual Insights', fontsize=24, fontweight='bold')
# Simple PMF showing exponential decay (using p = 0.3)
x_simple = np.arange(1, 11)
pmf_simple = stats.geom.pmf(x_simple, 0.3)
ax1.bar(x_simple, pmf_simple, alpha=0.8, color='steelblue', edgecolor='black', linewidth=1)
ax1.set_title('PMF: Exponential Decay Pattern', fontsize=18, fontweight='bold', pad=15)
ax1.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax1.set_ylabel('Probability', fontsize=14, fontweight='bold')
ax1.grid(True, alpha=0.3)
ax1.tick_params(axis='both', which='major', labelsize=14)
# Simple CDF showing approach to 1
cdf_simple = stats.geom.cdf(x_simple, 0.3)
ax2.plot(x_simple, cdf_simple, 'o-', linewidth=4, markersize=8, color='darkgreen')
ax2.set_title('CDF: Rapid Approach to Certainty', fontsize=18, fontweight='bold', pad=15)
ax2.set_xlabel('Number of Trials (X)', fontsize=17, fontweight='bold')
ax2.set_ylabel('Cumulative Probability', fontsize=14, fontweight='bold')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 1.05)
ax2.tick_params(axis='both', which='major', labelsize=14)
plt.tight_layout()
plt.show() 这段代码创建了一个聚焦式可视化图,重点突出几何分布的两个最重要的视觉特征。左侧面板展示了概率如何从第一次试验开始呈指数衰减,而右侧面板则展示了累积分布函数 (CDF) 中概率质量的快速累积。
尝试将成功概率从 0.3 改为其他值,例如 0.1 或 0.7,观察分布形状的变化。较低的概率会产生更平缓的概率质量函数 (PMF) 曲线和上升速度较慢的累积分布函数 (CDF),而较高的概率则会产生更陡峭的下降和更快趋向确定性的过程。
七、几何分布的无记忆性
几何分布具有独特的特征,使其与其他大多数离散分布区别开来。
7.1 无记忆特性
无记忆性指出,对于任意正整数 s 和 t,P(X > s + t | X > s) = P(X > t)。这意味着需要进行额外试验的概率与之前失败的试验次数无关。
从数学角度来看,这一性质源于 P(X > k) = (1-p) k,使得条件概率的计算变得简单明了。实际上,如果你已经经历了五次失败的面试,未来面试的概率分布与你最初开始面试时完全相同------过去的失败不会影响未来的概率。
7.2 与伯努利试验和实验的关系
几何实验中的每一次试验都代表一次独立的伯努利试验,其成功概率为常数 p。几何分布对这些试验序列进行建模,直到第一次成功,使其成为"等待时间"问题的离散模拟。
这种关系解释了为什么几何分布在质量控制中频繁出现,因为每个测试项目都代表一次伯努利试验,而我们的目标是检测出第一个缺陷产品。独立性假设确保了在早期测试中发现缺陷产品不会改变在后续测试中发现缺陷产品的概率。
7.3 与连续模拟物形成对比
指数分布是几何分布的连续对应物,两者都具有无记忆性。几何分布模拟离散的等待时间(试验次数),而指数分布模拟连续的等待时间(事件发生所需的时间)。
这两种分布在可靠性分析和排队论中都有应用。例如,几何分布可以用来模拟服务器首次发生故障前的请求次数,而指数分布可以用来模拟下一次服务器故障发生的时间。