论文笔记（一百零三）π0.6 : a VLA That Learns From Experience（二）

π0.6 : a VLA That Learns From Experience（二）

• 文章概括
• ABSTRACT
• [VI. EXPERIMENTAL EVALUATION](#VI. EXPERIMENTAL EVALUATION)
• • [A. 评估任务](#A. 评估任务)
  • [B. 对比实验与消融实验](#B. 对比实验与消融实验)
  • [C. 定量结果](#C. 定量结果)
• [VII. DISCUSSION AND FUTURE WORK](#VII. DISCUSSION AND FUTURE WORK)
• ACKNOWLEDGEMENTS
• APPENDIX
• • [A. 贡献分工](#A. 贡献分工)
  • [B. 额外的价值函数可视化](#B. 额外的价值函数可视化)
  • [C. 用于策略改进的对数似然计算](#C. 用于策略改进的对数似然计算)
  • [D. PPO implementation](#D. PPO implementation)
  • [E. 使用 CFG 在测试时通过 β > 1 β>1 β>1 改进策略](#E. 使用 CFG 在测试时通过 β > 1 β>1 β>1 改进策略)
  • [F. 额外的算法细节](#F. 额外的算法细节)

文章概括

引用：

@article{
}

主页：
原文：
代码、数据和视频：

系列文章：

请在 《 《 《文章 》 》 》 专栏中查找

---

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

---

ABSTRACT

我们研究视觉-语言-行动（vision-language-action, VLA）模型如何在真实世界部署中通过强化学习（reinforcement learning, RL）持续提升能力。 我们提出了一种通用方法------基于优势条件策略的经验与纠正强化学习（RL with Experience and Corrections via Advantage-conditioned Policies, RECAP），该方法通过"优势条件化"（advantage conditioning）为 VLA 模型提供强化学习训练机制。我们的方法将多种异质数据整合进模型的自我改进过程，包括示教数据、按当前策略（on-policy）采集的数据，以及在自主执行过程中由专家远程操控提供的干预数据。 RECAP 首先通过离线强化学习（offline RL）预训练一个通用型 VLA 模型，我们称之为 π 0.6 ∗ π_{0.6}^{\ast} π0.6∗，随后再通过在真实机器人上采集的数据对其进行专门化，从而在下游任务上获得高性能。 我们证明，使用完整 RECAP 流程训练得到的 π 0.6 ∗ π_{0.6}^{\ast} π0.6∗ 模型，能够在真实家庭场景中叠衣服、可靠地组装纸箱，并且可以操作专业意式咖啡机制作浓缩咖啡饮品。 在部分最困难的任务上，RECAP 使任务吞吐量提高了两倍以上，并将任务失败率大致降低了一半。

VI. EXPERIMENTAL EVALUATION

在实验评估中，我们使用 RECAP 在一组真实任务上训练 π0.6 模型：制作意式浓缩咖啡、折叠多样化衣物，以及组装纸箱。 每个任务都需要多个步骤，持续时间为 5 至 15 分钟，涉及复杂的操作行为（受约束的用力操作、倒液体、操作布料和纸板等），且需要快速执行以保证高吞吐量。 图 5 展示了我们实验中使用的机器人平台。 下面我们将介绍任务与基线的详细信息，之后给出量化实验。

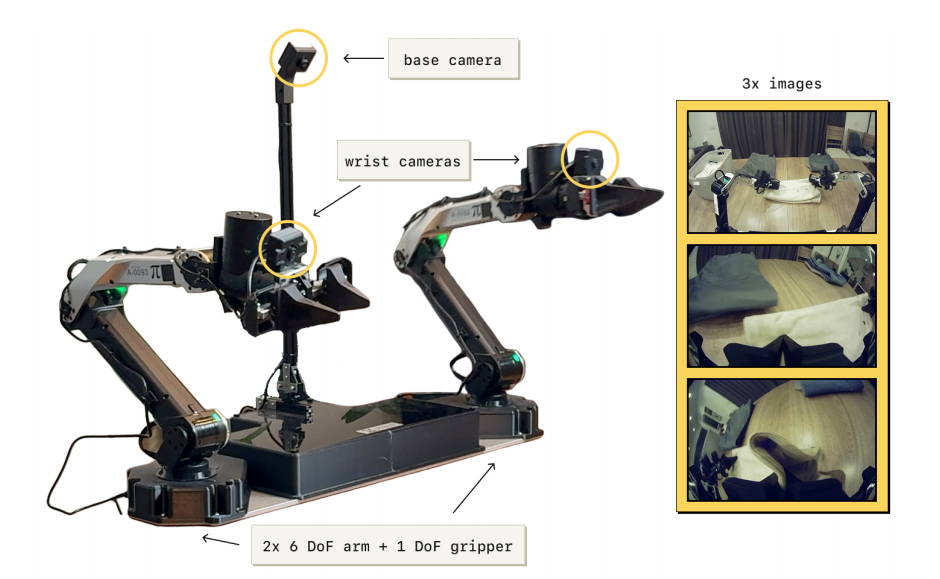图 5：我们实验中使用的机器人系统。 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 在预训练阶段使用来自多种机器人平台的数据。 在迭代改进实验中，我们使用一个固定的双臂系统，配备两个 6 自由度机械臂与平行夹爪。 机械臂以 50 Hz 的关节位置指令进行控制。 观测包括关节与夹爪位置，以及来自三台相机的图像： 一台安装在双臂之间的基座相机，以及每个机械臂腕部的一台相机。 该系统可以灵活安装，例如放置在桌面上。

A. 评估任务

我们的量化评估与对比包含三类任务，每类任务下有不同的变体：折衣、制作咖啡以及纸箱组装。 下面总结这些任务（图 6 中附有示意）：

折衣（T 恤与短裤）

这是 π0 论文 [81] 中的标准折衣任务。 其流程包括从篮子中取出一件 T 恤或短裤（初始状态可变化）、摊平并完成折叠。 成功标准是在 200 秒内将衣物折叠好并放在桌面右上角。

折衣（多样化衣物）

该任务要求折叠更多样的衣物，共 11 类，包括毛巾、衬衫、毛衣、牛仔裤、T 恤、短裤、POLO 杉、裙子、长袖衫、袜子与内衣。为了获得低方差指标，我们在实验中以最具挑战性的"衬衫"作为评估对象。不过，策略是在所有衣物上共同训练的，附带的视频展示了多种衣物的结果。成功定义为：在 500 秒内将目标衣物正确折叠并放置在桌面堆叠处。

折衣（特定失败模式消除）

折衣任务的最终版本为消融实验设计，具有更结构化的设置，其任务是从固定的、已摊开的初始状态折叠一件橙色 T 恤。我们非常强调成功，设定了严格的成功标准：必须在 200 秒内折叠正确，且衣领始终朝上。该任务被用于验证 RECAP 是否能通过 RL 移除特定不良行为（例如衣领朝下而非朝上）。

咖啡厅（双份意式浓缩）

我们在商业咖啡机上评估策略在一项极具挑战的长时间咖啡制作任务上的表现。尽管策略能制作多种饮品（拿铁、美式、意式浓缩等），甚至能用毛巾清洁咖啡机，但在量化实验中，我们聚焦于"双份意式浓缩"任务。该任务包括：拿起手柄、放到磨豆机研磨、压粉、锁入咖啡机、拿来杯子、萃取完整咖啡液、上饮品。成功标准是：在 200 秒内完成全部步骤，并无重大错误（如掉落手柄或洒出咖啡）。

纸箱组装

我们在真实工厂部署场景中评估策略在纸箱组装任务上的表现。纸箱组装包括：从摊平的纸板开始折叠纸箱、贴标签、并将其放入箱体指定位置。在量化实验中，我们对整个任务进行评估，成功定义为：在 600 秒内从纸板到完成组装并放置到堆叠位置。

B. 对比实验与消融实验

我们将 RECAP 与多个基线方法进行对比：

预训练的 π0.5 [5]。

该基线不使用 RL，也未使用 RECAP。

预训练的 π0.6 [6]。

它不包含优势指示器 I t I_t It，并通过监督学习进行预训练。

使用 RL 预训练的 π 0.6 ∗ π_{0.6}^{*} π0.6∗。

它与价值函数一起通过 RL 进行预训练，并包含第 V-D 节所述的优势指示器 I t I_t It。

π 0.6 ∗ π_{0.6}^{*} π0.6∗ offline RL + SFT.

该模型通过使用目标任务的示范数据微调 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 预训练 checkpoint 来训练。 我们将此微调称为 "SFT"，因为示范中的优势指示 I t I_t It 始终被设为 True。 我们发现，将"离线 RL 预训练的 π 0.6 ∗ π_{0.6}^{*} π0.6∗ "与高质量 SFT 结合，性能优于单纯的 SFT（即没有离线 RL 预训练的 SFT）， 并为进一步利用真实机器人数据进行 RL 提供了良好的起点。

π 0.6 ∗ π_{0.6}^{*} π0.6∗（我们的最终模型）

这是使用 RECAP 在目标任务上训练得到的最终模型，包括自主执行与专家纠正的数据。 默认情况下，我们在 β=1 时评估性能。 在部分实验中，我们也考虑使用 CFG（对应 β>1）进行推理。

我们还考虑了文献中的两种备选策略提取方法，用来与我们基于优势条件化的方案进行对比， 这两种方法都使用与 RECAP 相同的真实机器人数据，但采用了不同的策略学习方式：

AWR（Advantage Weighted Regression）

从同样的预训练 π0.6（不含优势条件化）开始，我们依据价值函数提取的优势值使用 AWR [68] 进行微调。

PPO

我们实现了 DPPO/FPO [23, 82] 的一种变体，其中基于单步 diffusion 目标来计算似然值， 并按照 SPO [83] 使用另一种 PPO 约束定义（详见附录 D）。

C. 定量结果

我们使用两个指标进行评估：吞吐量与成功率。 吞吐量衡量机器人每小时能成功执行多少次任务，因此同时反映速度与成功率。 成功率衡量成功 episode 的比例，由人工标注得到。 标注者会基于多个质量指标对 episode 进行评估，我们将这些指标汇总为最终的成功标记。

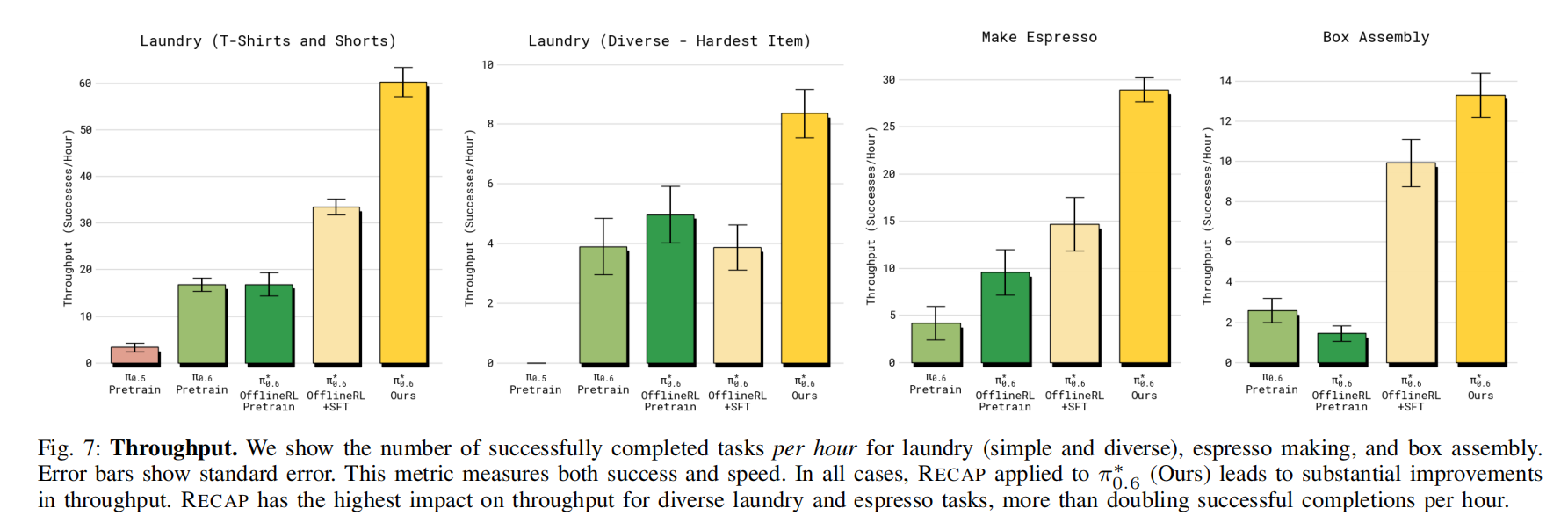
1）RECAP 提升策略的幅度有多大？ 为回答这个问题，我们在图 7 与图 8 中展示主要量化结果。 在所有任务中，最终的 π 0.6 π_{0.6} π0.6 都显著优于基础的监督版 π0.6、RL 预训练版 π 0.6 π_{0.6} π0.6、以及 offline RL + SFT 的 π 0.6 ∗ π_{0.6}^{*} π0.6∗。 在"多样化折衣任务"与"咖啡任务"中，由于加入真实机器人数据，吞吐量提升超过两倍（即 offline RL+SFT → 最终 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 的提升）， 失败率降低约一半。 在较简单的折衣任务（T 恤与短裤）中，SFT 阶段后成功率已接近上限， 但最终模型的吞吐量仍显著提升。

除多样化折衣外，最终 π 0 ∗ . 6 π_0^{*}.6 π0∗.6 在所有任务上的成功率均超过 90%。 这使得模型可以在真实场景中使用，例如办公室做咖啡或工厂组装纸箱（视频中展示）。 对纸箱组装任务，图 8（右）展示四个阶段的成功率：取纸板、折纸箱、贴标签、放置入箱。 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 在每个阶段的成功率都超过其他模型。 这些阶段的大部分失败都因"超时"而产生。 附带视频展示了机器人连续运行数小时完成任务的延时画面。

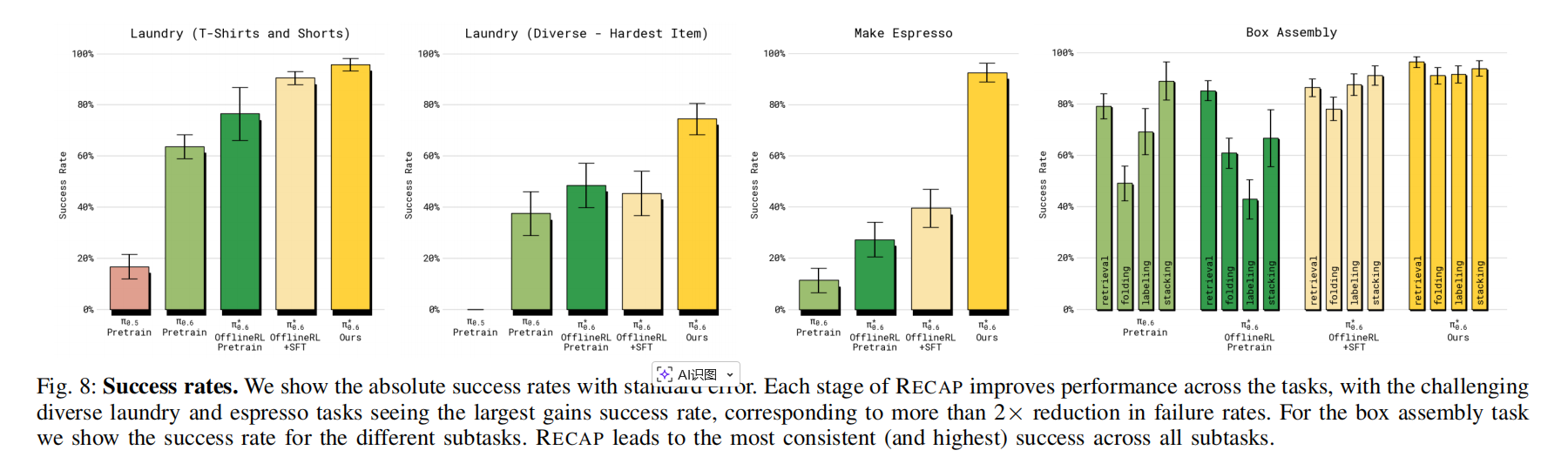
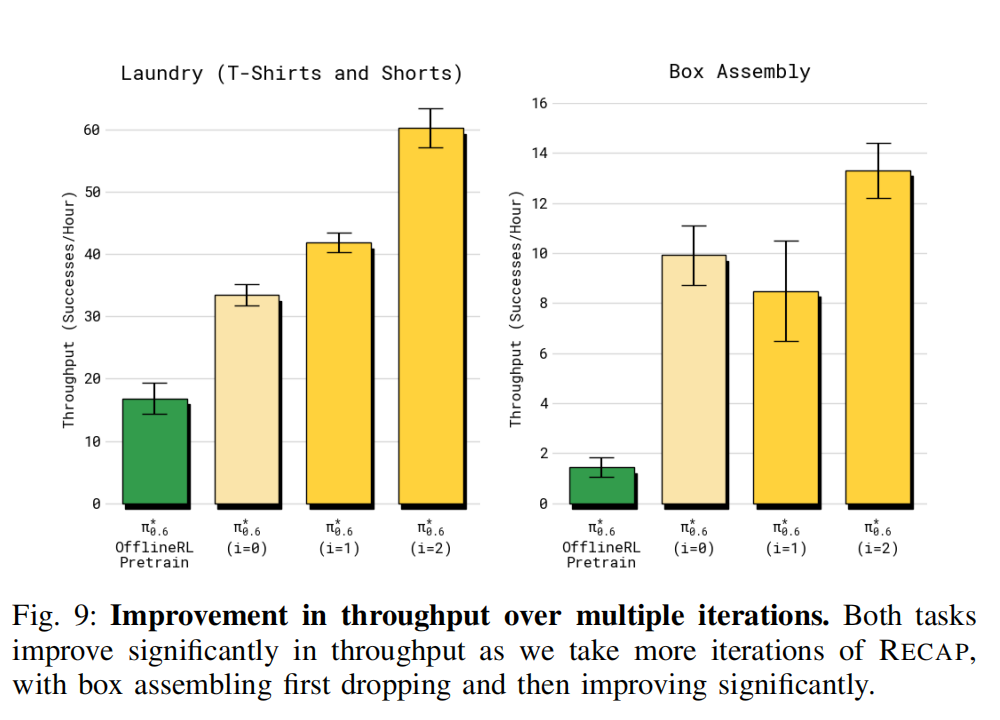
2）RECAP 在多轮迭代中能让 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 改进多少？： 接下来我们解释 RECAP 如何在多次数据收集和训练的迭代过程中不断提升策略性能。 我们研究了 T 恤与短裤折叠任务，以及纸箱组装任务。 对于 T 恤折叠任务，我们在两个迭代中仅使用自主执行（无人工干预）所收集的数据用于策略改进， 以评估 RECAP 是否能仅通过强化学习提升策略。 每次迭代，我们在四台机器人上共采集 300 条轨迹。 对于盒子组装任务，我们使用自主尝试和带有专家远程干预的尝试， 每轮迭代包括 600 次自主尝试及 360 次专家干预尝试。

我们在图 9 中绘制了各迭代的吞吐量，对比两轮 RECAP（分别标记为 i = 1 与 i = 2）。 最终一轮（标记为 Ours）对应前一节展示的最佳结果。 我们还比较了最初用于收集数据的策略，它由离线 RL 预训练的 π0∗.6 模型经 SFT 微调得到。 对于两个任务，π0∗.6 在两轮迭代中均有所提升。 在洗衣折叠任务中可以看到稳定的提升，最终吞吐量提高约 50%。 对于长时间跨度的纸箱组装任务，需要更多数据才能产生显著提升， 但在第二轮迭代后，吞吐量提高了两倍。

我们在图 10 中展示了各轮迭代的成功率。 在洗衣任务中，第一轮迭代就将成功率提升到了 90% 以上，而第二轮主要提升吞吐量。 在纸箱组装任务中，两轮迭代的成功率均明显提升。 虽然仍存在失败（尤其是在将箱子放到成品堆时）， 最终策略在折叠箱体和贴标签两个阶段均达到了约 90% 的成功率， 且都在 600 秒的限定时间内完成。

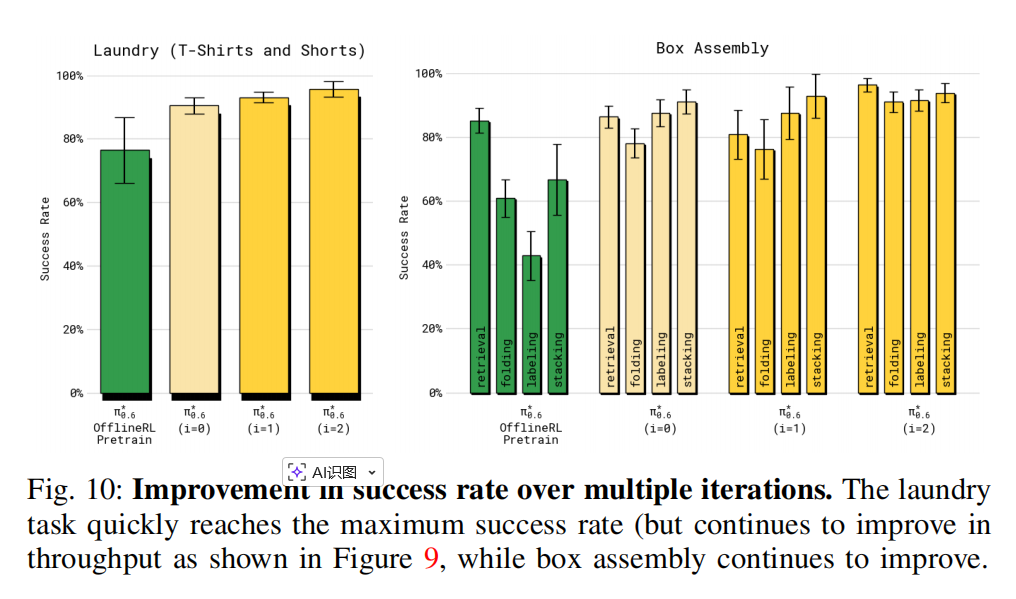
3）RECAP 的优势条件化策略提取与其他方法相比效果如何？： 我们将第 IV-B 节提出的优势条件化策略提取方法，与文献中的其他方法（AWR 与 PPO）进行比较。 对比实验采用 T 恤与短裤折叠任务。 为确保公平比较，所用数据与我们训练最终模型时完全一致。 这实际上给了基线模型一点优势，因为这些数据是在 RECAP 运行期间采集的，更加优质。 结果如图 11 所示。 虽然 AWR 与 PPO 都能取得一定表现，但都远不及我们的方法， 甚至难以超越"离线 RL + SFT"的 π 0.6 ∗ π_{0.6}^{*} π0.6∗ 基线。 对于 PPO，我们不得不在这种离线环境中使用非常小的 trust-region 约束（η = 0.01）来稳定训练， 虽然训练变得稳定，但性能依然不佳。 AWR 能获得还可以的成功率，但策略执行速度明显变慢，吞吐量显著降低。

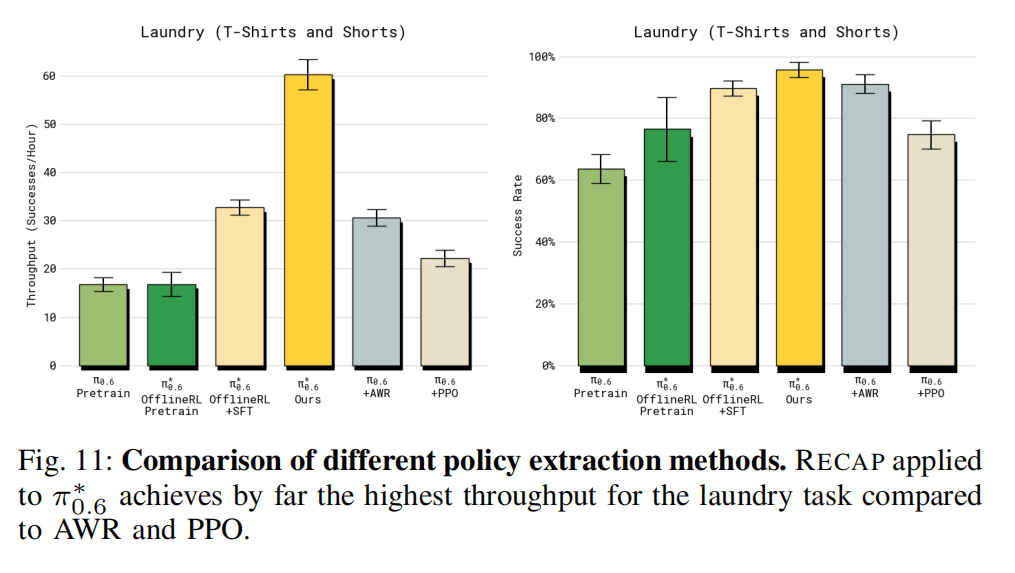
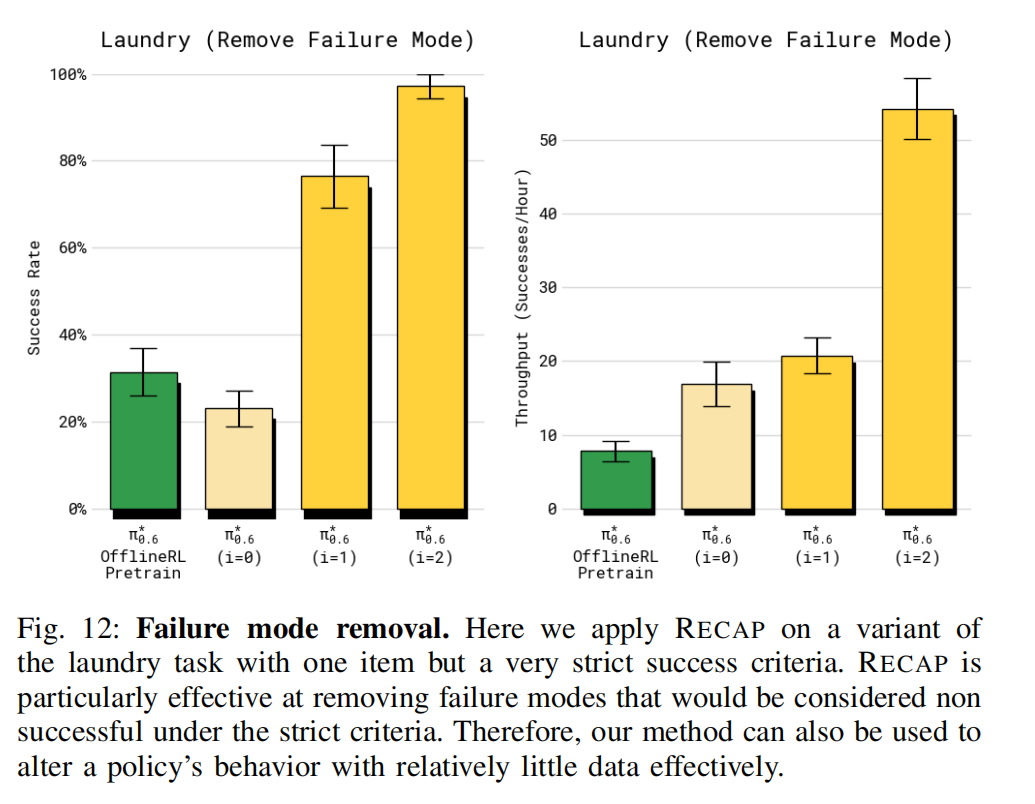
4）RECAP 是否能在少量数据下显著改变策略行为、并消除某种失败模式？： 前述实验主要聚焦于整体端到端的策略表现， 我们还可以聚焦某个具体失败模式，检验 RECAP 的强化学习是否能去除某个特定错误。 为此，我们使用了具有严格成功标准的洗衣任务版本， 任务要求策略必须把 T 恤折叠好且衣领居中朝上。 每个 episode 都在特定的对抗性初始条件下开始， 此时 T 恤被摆放成 baseline（离线 RL + SFT）常常折不好 的状态。 如图 12 所示，在此设置下进行两轮 RECAP（每轮采集 600 条轨迹），最终策略成功率达 97%， 且执行速度很快。 因此我们得出结论：RECAP 能够有效消除特定失败模式， 即使完全依赖 RL（无需人工干预数据或额外示范）也能做到。

VII. DISCUSSION AND FUTURE WORK

训练能够在真实世界任务中达到与人类同等的稳健性、速度与流畅性的策略，是机器人学习中的一项重大挑战。 本文讨论了如何通过结合 DAgger 式示范指导与强化学习（RL）的经验学习来应对这一挑战。 我们介绍了 RECAP，这是一种利用自主尝试、奖励反馈与人工干预来训练 VLA 的方法， 并展示了使用 RECAP 训练的模型 π0∗.6 在一系列真实任务（制作浓缩咖啡、折叠多种衣物、组装纸箱）上的实验结果。 RECAP 的核心是一个非常适合对 VLA 策略进行可扩展训练的强化学习方法， 它使用基于价值函数的"优势条件化"进行策略提取。 该 RL 方法的数据来自自主执行与人工干预的结合， 人工干预用来纠正大错误，自主数据用来细化行为。 我们的实验表明，RECAP 能同时提升策略的成功率和吞吐量， 在一些难度较高的任务上吞吐量超过两倍提升，同时失败次数减少约两倍。

RECAP 仍有多个可改进方向。 首先，我们的系统尚未完全自动化：奖励反馈、干预、episode 重置仍依赖人工标注和人工操作。 已有研究探索了自动化这些环节的方法 [84,85]， 而 VLA 又提供了实现更自动化数据收集的新机会， 例如利用高层策略 [86] 来推理并自动重置场景。 其次，我们的系统在探索策略方面相对朴素： 探索主要依赖策略的随机性与人工干预，而不是高级探索方法。 当初始模仿策略已经能执行相对合理行为时，这样做是可以接受的， 但仍有大量改善空间，可以引入更先进的探索算法。 最后，RECAP 使用迭代式"离线"更新...... 即"收集一批数据 → 训练 → 重复"形式， 而不是实时更新策略与价值函数的完全在线强化学习。 我们出于工程便利做出了此选择， 但将其扩展为完全并发的在线 RL 框架，是一个非常有前景的研究方向。

更广泛地说，利用 RL 训练 VLA 可能是使其达到真实世界性能的最直接路径。 但将 RL 应用于 VLA 仍面临多个挑战， 包括大规模模型的训练难度、样本效率问题、自主性、以及延迟奖励等。 尽管现有用于小规模系统或虚拟领域（如 LLM）的 RL 框架可作为起点， 但仍需要大量研究才能让 RL 成为 VLA 训练的实用工具。 我们希望本工作能成为迈向该方向的一步。

ACKNOWLEDGEMENTS

我们感谢机器人操作者在数据收集、评估、后勤和视频录制方面的贡献， 也感谢技术人员对机器人维护与修理的支持。 完整贡献声明见附录 A。

APPENDIX

A. 贡献分工

数据采集与实验运行：Michael Equi，Chelsea Finn，Lachy Groom，Hunter Hancock，Karol Hausman，Rowan Jen， Liyiming Ke ，Marinda Lamb，Vishnu Mano，Suraj Nair，Charvi Sharma，Laura Smith，Will Stoeckle，Anna Walling，Blake Williams。

标注与补充数据：Chelsea Finn，Catherine Glossop，Hunter Hancock，Brian Ichter，Rowan Jen， Liyiming Ke ，Chandra Kuchi，Karl Pertsch，Laura Smith，Will Stoeckle，Quan Vuong，Anna Walling。

策略训练与研究：Ashwin Balakrishna，Kevin Black，Danny Driess，Michael Equi， Yunhao Fang ，Chelsea Finn，Catherine Glossop，Karol Hausman，Gashon Hussein，Brian Ichter， Liyiming Ke ，Sergey Levine， Yao Lu ，Suraj Nair，Karl Pertsch，Allen Z. Ren，Lucy Shi，Laura Smith，Jost Tobias Springenberg，Kyle Stachowicz，Alex Swerdlow，Marcel Torne，Quan Vuong，Lili Yu， Zhiyuan Zhou 。

策略基础设施：Kevin Black，Karan Dhabalia，Danny Driess，Michael Equi， Liyiming Ke ，Adrian Li，Suraj Nair，Allen Z. Ren，Laura Smith，Jost Tobias Springenberg，Kyle Stachowicz，Alex Swerdlow， Haohuan Wang ，Ury Zhilinsky， Zhiyuan Zhou 。

机器人硬件：Ali Amin，Raichelle Aniceto，Grace Connors，Adnan Esmail，Thomas Godden，Ivan Goryachev，Tim Jones，Ben Katz，Devin LeBlanc，Mohith Mothukuri，Sukwon Yoo。

机器人基础设施：Ken Conley，James Darpinian，Jared DiCarlo，Karol Hausman，Szymon Jakubczak，James Tanner。

论文撰写与插图：Kevin Black，Danny Driess，Michael Equi，Chelsea Finn，Hunter Hancock，Karol Hausman，Brian Ichter， Liyiming Ke ，Sergey Levine，Suraj Nair，Allen Z. Ren，Laura Smith，Jost Tobias Springenberg， Zhiyuan Zhou 。

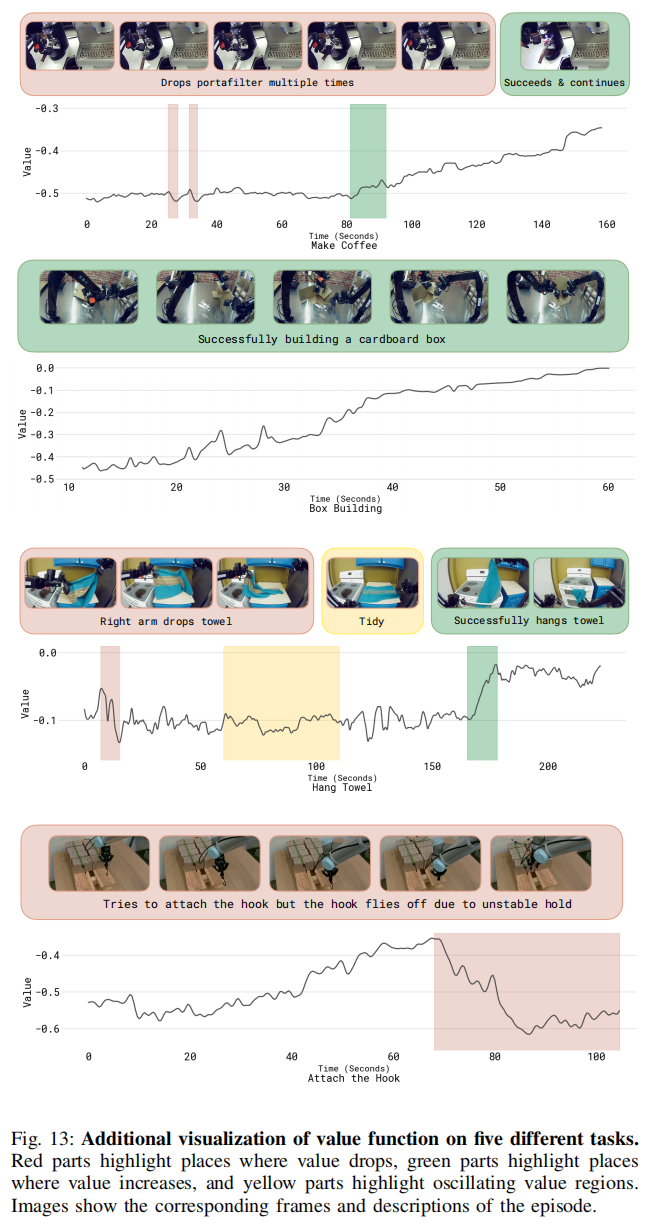
B. 额外的价值函数可视化

图 13 展示了我们训练好的价值函数在五个不同任务上的额外可视化结果， 包括用于评估策略的任务（制作浓缩咖啡、组装纸箱）， 以及更广泛的任务（挂毛巾、装挂钩）。 其中变化最明显的部分被高亮标出：红色表示价值函数下降的部分， 绿色表示价值函数上升的部分， 黄色表示价值值震荡波动的位置。 图像展示了对应的帧以及该 episode 的描述。

C. 用于策略改进的对数似然计算

论文的 flow-based 连续动作模型没有封闭形式的 log-likelihood，那么它的"对数似然"到底怎么算？

因为 RECAP 的优势条件化训练要用：

log ⁡ π θ ( a t : t + H ∣ ⋅ ) \log \pi_\theta(\text{a}_{t:t+H}\mid \cdot) logπθ(at:t+H∣⋅)

但是：

• 连续动作是用 flow matching / diffusion 训练的
• 这类模型没有直接的公式表达出来的概率密度函数
• 不能像普通高斯一样直接写 log p(a)

所以这一节的任务是：

推导一个"对数似然的下界（ELBO）"，保证模型在训练中最大化这个下界即可。

为了从公式（4）推导对数似然，我们首先注意到整个模型的似然可以分解为自回归项与扩散项：
π θ ( a t : t + H , a t : t + H ℓ , ℓ ^ ∣ I t , o t , ℓ ) = π θ ( a t : t + H ∣ I t , o t , ℓ , ℓ ^ ) π θ ( a t : t + H ℓ ∣ I t , o t , ℓ , ℓ ^ ) π θ ( ℓ ^ ∣ I t , o t , ℓ ) (6) \pi_\theta(\text{a}{t:t+H}, \text{a}^\ell{t:t+H}, \hat{\ell} \mid I_t, \text{o}t, \ell) = \\ \pi\theta(\text{a}{t:t+H} \mid I_t, \text{o}t, \ell, \hat{\ell}) \pi\theta(\text{a}^\ell{t:t+H} \mid I_t, \text{o}t, \ell, \hat{\ell}) \pi\theta(\hat{\ell} \mid I_t, \text{o}_t, \ell) \tag{6} πθ(at:t+H,at:t+Hℓ,ℓ^∣It,ot,ℓ)=πθ(at:t+H∣It,ot,ℓ,ℓ^)πθ(at:t+Hℓ∣It,ot,ℓ,ℓ^)πθ(ℓ^∣It,ot,ℓ)(6)

其中第一项使用 flow matching 建模， 第二项是离散动作 a t : t + H ℓ \text{a}^\ell_{t:t+H} at:t+Hℓ 的自回归似然， 第三项对应文本输出的自回归似然。 自回归似然可以使用常规方式计算，即对真实 token 施加交叉熵损失。 对于连续动作 a t : t + H \text{a}_{t:t+H} at:t+H，没有可用的封闭形式似然 [79]。

第一步：把整体似然拆成三部分（公式 6）

论文的动作输出包含三种东西：

1. 连续动作片段 ( a t : t + H \text{a}_{t:t+H} at:t+H)
2. 这些动作的 token 化表示 ( a t : t + H ℓ \text{a}^\ell_{t:t+H} at:t+Hℓ)（用于 KI 与离散动作建模）
3. 高层文本子任务预测 ( ℓ ^ \hat\ell ℓ^)

所以整体概率可以分解为：

π θ ( a t : t + H , a t : t + H ℓ , ℓ ^ ∣ I t , o t , ℓ ) = π θ ( a t : t + H ∣ I t , o t , ℓ , ℓ ^ ) π θ ( a t : t + H ℓ ∣ I t , o t , ℓ , ℓ ^ ) π θ ( ℓ ^ ∣ I t , o t , ℓ ) (6) \pi_\theta(\text{a}{t:t+H}, \text{a}^\ell{t:t+H}, \hat{\ell} \mid I_t, \text{o}t, \ell) = \\ \pi\theta(\text{a}{t:t+H} \mid I_t, \text{o}t, \ell, \hat{\ell}) \pi\theta(\text{a}^\ell{t:t+H} \mid I_t, \text{o}t, \ell, \hat{\ell}) \pi\theta(\hat{\ell} \mid I_t, \text{o}_t, \ell) \tag{6} πθ(at:t+H,at:t+Hℓ,ℓ^∣It,ot,ℓ)=πθ(at:t+H∣It,ot,ℓ,ℓ^)πθ(at:t+Hℓ∣It,ot,ℓ,ℓ^)πθ(ℓ^∣It,ot,ℓ)(6)

理解：

• 第三项：文本子任务 → 普通语言模型 → 交叉熵
• 第二项：离散动作 token → 交叉熵
• 第一项 ：连续动作 → 用 flow matching，没法直接写似然！

这一节要解决的就是 第一项。

然而我们可以按照先前工作 [82]，将一步扩散过程视为高斯分布，其似然为：

log ⁡ π θ ( a t : t + H ∣ a 1 : H η , ω , I t , o t , ℓ , ℓ ^ ) = log ⁡ N ( ω − f θ ( a 1 : H η , ω , I t , o t , ℓ , ℓ ^ ) , I ) (7) \log \pi_\theta(\text{a}{t:t+H} \mid \text{a}^{\eta,\omega}{1:H}, I_t, \text{o}t, \ell, \hat{\ell}) = \\ \log \mathcal{N}\big(\omega - f\theta(\text{a}^{\eta,\omega}_{1:H}, I_t, \text{o}_t, \ell, \hat{\ell}), I\big) \tag{7} logπθ(at:t+H∣a1:Hη,ω,It,ot,ℓ,ℓ^)=logN(ω−fθ(a1:Hη,ω,It,ot,ℓ,ℓ^),I)(7)

其中：
a t : t + H η , ω = η a t : t + H + ( 1 − η ) ω \text{a}^{\eta,\omega}{t:t+H} = \eta \text{a}{t:t+H} + (1 - \eta)\omega at:t+Hη,ω=ηat:t+H+(1−η)ω，且 ω ∼ N ( 0 , I ) \omega \sim \mathcal{N}(0, I) ω∼N(0,I)。

第二步：flow matching 的连续动作如何写似然？（公式 7）

flow matching / diffusion 做的是：

把真实动作 a 和噪声 ω 混合成一个中间状态 a^{η,ω}， 再训练模型 fθ 去"预测噪声成分"，本质是一个 MSE 去噪任务。

所以单步扩散可以当成一个 Gaussian：

a η , ω = η a + ( 1 − η ) ω \text{a}^{\eta,\omega} = \eta \text{a} + (1-\eta)\omega aη,ω=ηa+(1−η)ω

模型要做的是：

ω ≈ a + f θ ( a η , ω , ⋅ ) \omega \approx \text{a} + f_\theta(\text{a}^{\eta,\omega}, \cdot) ω≈a+fθ(aη,ω,⋅)

所以 likelihood 可以写成高斯分布：

log ⁡ π θ ( a ∣ a η , ω , I , o , ℓ , ℓ ^ ) = log ⁡ N ( ω − f θ ( ⋅ ) , I ) (7) \log \pi_\theta(\text{a}\mid \text{a}^{\eta,\omega},I,\text{o},\ell,\hat\ell) = \log \mathcal{N}(\omega - f_\theta(\cdot), I) \tag{7} logπθ(a∣aη,ω,I,o,ℓ,ℓ^)=logN(ω−fθ(⋅),I)(7)

解释成人话：

• diffusion 模型在训练时，其实是在预测"噪声"（或者速度场）
• 所以"模型预测对噪声的误差"可以直接写成一个高斯的 log-likelihood
• 这就是公式 (7)

换句话说：

flow matching = 预测噪声的 MSE = 对连续动作的 Gaussian log-likelihood

根据 [80,82] 的推导，我们可以对似然构建证据下界（ELBO）， （等价于对 η 和 ω 做边缘化） 从而得到：
log ⁡ π θ ( a t : t + H ∣ I t , o t , ℓ , ℓ ^ ) ≥ 1 2 E η , ω [ − w ( η ) , ∥ ω − a 1 : H − f θ ( a 1 : H η , ω , I t , o t , ℓ , ℓ ^ ) ∥ 2 ] + c (8) \log \pi_\theta(\text{a}{t:t+H}\mid I_t, \text{o}t, \ell, \hat{\ell}) \ge \\ \frac12 \mathbb{E}{\eta,\omega}\Big[ - w(\eta), \lVert \omega - \text{a}{1:H} - f_\theta(\text{a}^{\eta,\omega}_{1:H}, I_t, \text{o}_t, \ell, \hat{\ell}) \rVert^2 \Big] + c \tag{8} logπθ(at:t+H∣It,ot,ℓ,ℓ^)≥21Eη,ω[−w(η),∥ω−a1:H−fθ(a1:Hη,ω,It,ot,ℓ,ℓ^)∥2]+c(8)

其中 w ( η ) = e − η / 2 w(\eta)=e^{-\eta/2} w(η)=e−η/2 是噪声相关的权重， c \text{c} c 是与 f θ f_\theta fθ 无关的常数。 详细推导见 [80]，其中附录 D.3 也推导了在该权重设定下 flow matching 与 diffusion 的关系。

第三步：对 η η η 和 ω ω ω 做期望（边缘化）得到 ELBO（公式 8）

但问题来了：

• 上面只是"单个 η η η 和 ω ω ω 的似然"
• 实际模型需要"对所有可能的加噪状态"都成立

所以我们对 η η η 和 ω ω ω 取期望：

log ⁡ π θ ( a ∣ I , o , ℓ , ℓ ^ ) ≥ 1 2 E η , ω [ − w ( η ) ∣ ω − a − f θ ( a η , ω , ⋅ ) ∣ 2 ] + c (8) \log \pi_\theta(\text{a}\mid I,\text{o},\ell,\hat\ell) \ge \frac12 \mathbb{E}{\eta,\omega}\Big[- w(\eta) | \omega - \text{a} - f\theta(\text{a}^{\eta,\omega},\cdot)|^2 \Big] + c \tag{8} logπθ(a∣I,o,ℓ,ℓ^)≥21Eη,ω[−w(η)∣ω−a−fθ(aη,ω,⋅)∣2]+c(8)

这里：

• w ( η ) = e − η / 2 w(\eta) = e^{-\eta/2} w(η)=e−η/2 是噪声相关权重
• c c c 是常数（和 f θ f_θ fθ 无关，可以忽略）
• 目标就是最小化"预测噪声的 MSE"

解释：

模型越擅长"去噪"，得到的 log-likelihood 下界就越高。 所以"去噪误差(MSE)"就是连续动作的训练损失。

非常关键：

🎯 flow matching 的损失 = 似然的负 ELBO ≈ noise-prediction MSE

最后，将此下界与文本输出中离散动作的自回归似然结合，并把所有权重吸收到 α α α 中，可得：

log ⁡ π θ ( a t : t + H , a t : t + H ℓ ∣ I t , o t , ℓ , ℓ ^ ) ≥ E η , ω [ log ⁡ p θ ( a t : t + H ℓ ∣ I t , o t , ℓ , ℓ ^ ) − α η ∥ ω − a 1 : H − f θ ( a 1 : H η , ω , I t , o t , ℓ , ℓ ^ ) ∥ 2 ] (9) \log \pi_\theta(\text{a}{t:t+H}, \text{a}^\ell{t:t+H}\mid I_t, \text{o}t, \ell, \hat{\ell}) \ge \\ \mathbb{E}{\eta,\omega}\Big[ \log p_\theta(\text{a}^\ell_{t:t+H}\mid I_t, \text{o}t, \ell, \hat{\ell}) \\ -\alpha\eta \lVert \omega - \text{a}{1:H} - f\theta(\text{a}^{\eta,\omega}_{1:H}, I_t, \text{o}_t, \ell, \hat{\ell}) \rVert^2 \Big] \tag{9} logπθ(at:t+H,at:t+Hℓ∣It,ot,ℓ,ℓ^)≥Eη,ω[logpθ(at:t+Hℓ∣It,ot,ℓ,ℓ^)−αη∥ω−a1:H−fθ(a1:Hη,ω,It,ot,ℓ,ℓ^)∥2](9)

这就是论文主体部分给出的下界。

第四步：合并离散动作似然 + 连续动作 ELBO → 得到公式(9)

离散动作：

log ⁡ p θ ( a ℓ ∣ ⋅ ) \log p_\theta(\text{a}^\ell|\cdot) logpθ(aℓ∣⋅)

连续动作（来自公式 8）：

− α η ∣ ω − a − f θ ( a η , ω ) ∣ 2 -\alpha_\eta |\omega - \text{a} - f_\theta(\text{a}^{\eta,\omega})|^2 −αη∣ω−a−fθ(aη,ω)∣2

合并就得到：

log ⁡ π θ ( a , a ℓ ∣ ⋅ ) ≥ E η , ω [ log ⁡ p θ ( a ℓ ∣ ⋅ ) − α η ∣ ω − a − f θ ( a η , ω ) ∣ 2 ] (9) \log \pi_\theta(\text{a}, \text{a}^\ell|\cdot) \ge \mathbb{E}{\eta,\omega}\Big[ \log p\theta(\text{a}^\ell|\cdot) -\alpha_\eta |\omega - \text{a} - f_\theta(\text{a}^{\eta,\omega})|^2 \Big] \tag{9} logπθ(a,aℓ∣⋅)≥Eη,ω[logpθ(aℓ∣⋅)−αη∣ω−a−fθ(aη,ω)∣2](9)

也就是：

对离散动作：交叉熵
对连续动作：flow matching MSE
两者一起构成动作的似然下界

---

🎉 最终总结（你必须理解的核心一句话）

RECAP 需要 log π(a|s)。 但是连续动作的 flow matching 模型没有封闭形式似然。 所以论文用 diffusion / flow theory，把"去噪误差 MSE"当成 log-likelihood 的下界（ELBO）。 最终得到： 交叉熵（离散动作）+ 去噪 MSE（连续动作）= 整体动作似然下界。

D. PPO implementation

我们实现了一个与 DPPO 和 FPO [23, 82] 相关的 PPO [66] 变体，并将其作为额外的基线方法。 为了能够以计算高效的方式同时训练模型的自回归部分和基于扩散的动作专家，我们仅基于单步扩散目标来计算似然。

具体来说，我们使用一个与上节方程（9）类似的似然下界，但不包含改进指示器。 将其分解为自回归项与 flow-matching 项，可以写成：

log ⁡ π θ ( a t : t + H , a t : t + H ℓ ∣ o t , ℓ , ℓ ^ ) ≥ E η , ω [ log ⁡ p θ ( a t : t + H ℓ ∣ o t , ℓ , ℓ ^ ) − α η ∣ ∣ ω − a 1 : H − f θ ( a 1 : H η , ω , o t , ℓ , ℓ ^ ) ∣ ∣ 2 ] . (10) \log \pi_\theta(\text{a}{t:t+H}, \text{a}^{\ell}{t:t+H} \mid \text{o}t, \ell, \hat{\ell}) \ge \\ \mathbb{E}{\eta,\omega} \Big[ \log p_\theta(\text{a}^{\ell}{t:t+H} \mid \text{o}t, \ell, \hat{\ell})\\ -\alpha\eta || \omega - \text{a}{1:H} - f_\theta(\text{a}^{\eta,\omega}_{1:H}, \text{o}_t, \ell, \hat{\ell}) ||^2 \Big]. \tag{10} logπθ(at:t+H,at:t+Hℓ∣ot,ℓ,ℓ^)≥Eη,ω[logpθ(at:t+Hℓ∣ot,ℓ,ℓ^)−αη∣∣ω−a1:H−fθ(a1:Hη,ω,ot,ℓ,ℓ^)∣∣2].(10)

这与 FPO [82] 中使用的扩散似然下界类似。 我们将其与一种分为"扩散部分"和"自回归部分"的 PPO 风格损失相结合。 在初步实验中，我们发现：在我们的设置中，使用标准 PPO clipping 目标时，难以对动作专家（其动作由无界的 diffusion head 建模）施加有效的信赖域约束。 推测原因之一是我们的方法是"离线式"的，我们无法在每几个梯度步骤后就从真实机器人重新收集数据。 为了稳定训练，我们发现采用 SPO [83] 提出的另一种 PPO 约束定义更有效。 最终的损失函数如下所示：

L S P O + C o V L A ( θ ) = { π θ ( a i ∈ ℓ ^ ∣ o t , ℓ ) π ref ( a i ∈ ℓ ^ ∣ o t , ℓ ) A ref ( o t , a t , ℓ ) − ∣ A ref ( o t , a t , ℓ ) ∣ 2 ϵ ar [ π θ ( a ℓ ^ ∈ ℓ ^ ∣ o t , ℓ ) π ref ( a ℓ ^ ∈ ℓ ^ ∣ o t , ℓ ) − 1 ] } + α { π θ ( a t : t + H ∣ o t , ℓ ) π ref ( a t : t + H ∣ o t , ℓ ) A ref ( o t , a t , ℓ ) − ∣ A ref ( o t , a t , ℓ ) ∣ 2 ϵ flow [ π θ ( a t : t + H ∣ o t , ℓ ) π ref ( a t : t + H ∣ o t , ℓ ) − 1 ] } . (11) \mathcal{L}{{SPO+CoVLA}}(\theta) = \\ \Bigg\{ \frac{\pi\theta(a_i \in \hat{\ell} \mid o_t,\ell)}{\pi_{\text{ref}}(a_i \in \hat{\ell} \mid o_t,\ell)} A^{\text{ref}}(o_t,a_t,\ell) \\ -\frac{|A^{\text{ref}}(o_t,a_t,\ell)|}{2\epsilon_{\text{ar}}} \left[ \frac{\pi_\theta(a_{\hat{\ell}} \in \hat{\ell} \mid \text{o}t,\ell)}{\pi{\text{ref}}(a_{\hat{\ell}} \in \hat{\ell} \mid \text{o}t,\ell)} -1 \right] \Bigg\} \\ +\alpha\Bigg\{ \frac{\pi\theta(\text{a}{t:t+H}\mid \text{o}t,\ell)}{\pi{\text{ref}}(\text{a}{t:t+H}\mid \text{o}t,\ell)} A^{\text{ref}}(o_t,a_t,\ell) \\ -\frac{|A^{\text{ref}}(o_t,a_t,\ell)|}{2\epsilon{\text{flow}}} \left[\frac{\pi_\theta(\text{a}{t:t+H}\mid \text{o}t,\ell)}{\pi{\text{ref}}(\text{a}{t:t+H}\mid \text{o}_t,\ell)} - 1\right] \Bigg\}. \tag{11} LSPO+CoVLA(θ)={πref(ai∈ℓ^∣ot,ℓ)πθ(ai∈ℓ^∣ot,ℓ)Aref(ot,at,ℓ)−2ϵar∣Aref(ot,at,ℓ)∣[πref(aℓ^∈ℓ^∣ot,ℓ)πθ(aℓ^∈ℓ^∣ot,ℓ)−1]}+α{πref(at:t+H∣ot,ℓ)πθ(at:t+H∣ot,ℓ)Aref(ot,at,ℓ)−2ϵflow∣Aref(ot,at,ℓ)∣[πref(at:t+H∣ot,ℓ)πθ(at:t+H∣ot,ℓ)−1]}.(11)

其中 α α α 是权衡参数， ϵ a r ϵ_{ar} ϵar 与 ϵ f l o w ϵ_{flow} ϵflow 分别是自回归部分与 flow-matching 部分的信赖域系数。 我们使用该 PPO 变体，从 π0.6 的检查点开始，在评估数据上进行训练。

E. 使用 CFG 在测试时通过 β > 1 β>1 β>1 改进策略

在训练结束后，我们可以在式（2）中将 β > 1 β>1 β>1，以进一步"锐化"用于评估的策略分布。 如先前工作[4]所示，我们无需额外训练就可以恢复这一被锐化的策略， 因为该策略由已经学到的两个策略 π θ ( a t : t + H ∣ I t , o t , ℓ ) π_θ(\text{a}_{t:t+H}\mid I_t,\text{o}t,ℓ) πθ(at:t+H∣It,ot,ℓ)与 π θ ( a t : t + H ∣ o t , ℓ ) π_θ(\text{a}{t:t+H}\mid \text{o}_t,ℓ) πθ(at:t+H∣ot,ℓ)隐式定义。 具体来说，在训练之后我们可以构造如下近似 ：

π ^ ( a t : t + H ∣ o t , ℓ ) ∝ π ref ( a t : t + H ∣ o t , ℓ ) ( π ref ( a t : t + H ∣ I t , o t , ℓ ) π ref ( a t : t + H ∣ o t , ℓ ) ) β . (12) \hat{\pi}(\text{a}{t:t+H}\mid \text{o}t,\ell)\ \propto\ \pi{\text{ref}}(\text{a}{t:t+H}\mid \text{o}t,\ell) \left( \frac{\pi{\text{ref}}(\text{a}{t:t+H}\mid I_t,\text{o}t,\ell)} {\pi{\text{ref}}(\text{a}{t:t+H}\mid \text{o}t,\ell)} \right)^{\beta}. \tag{12} π^(at:t+H∣ot,ℓ) ∝ πref(at:t+H∣ot,ℓ)(πref(at:t+H∣ot,ℓ)πref(at:t+H∣It,ot,ℓ))β.(12) 此时我们可以注意到，扩散模型实际上学到的是似然的梯度， 也就是说，它分别表示 ∇ a log ⁡ π θ ( a t : t + H ∣ I t , o t , ℓ ) ∇\text{a} \log π_θ(\text{a}{t:t+H}\mid I_t,\text{o}t,ℓ) ∇alogπθ(at:t+H∣It,ot,ℓ)与 ∇ a log ⁡ π θ ( a t : t + H ∣ o t , ℓ ) ∇\text{a} \log π_θ(\text{a}{t:t+H}\mid \text{o}_t,ℓ) ∇alogπθ(at:t+H∣ot,ℓ)。

基于这一点，按照 Frans 等人[4]的做法，我们可以看到：如果在推理时沿着下式给出的梯度运行 flow-matching，

∇ a log ⁡ π θ ( a t : t + H ∣ o t , ℓ ) + β ( ∇ a log ⁡ π θ ( a t : t + H ∣ I t , o t , ℓ ) − ∇ a log ⁡ π θ ( a t : t + H ∣ o t , ℓ ) ) , (13) \nabla_\text{a} \log \pi_\theta(\text{a}{t:t+H}\mid \text{o}t,\ell)+ \\ \beta\Big( \nabla\text{a} \log \pi\theta(\text{a}{t:t+H}\mid I_t,\text{o}t,\ell)- \nabla\text{a} \log \pi\theta(\text{a}_{t:t+H}\mid \text{o}_t,\ell) \Big), \tag{13} ∇alogπθ(at:t+H∣ot,ℓ)+β(∇alogπθ(at:t+H∣It,ot,ℓ)−∇alogπθ(at:t+H∣ot,ℓ)),(13)

那么我们实际上就是在从目标的"加权/锐化后"的分布中采样。 需要指出的是，如正文中所述，参数 β β β与我们在训练时使用的优势阈值 ϵ ℓ ϵ_ℓ ϵℓ之间存在一种较为宽松的对应关系， 即二者都在"锐化"分布------前者在推理阶段，后者在训练阶段。 我们发现，如果在训练结束后将 β β β设得过大，在推理时对分布进行锐化会把动作分布推向其已学习支持集的边界， 这可能导致动作过于激进， 因此我们主要依靠训练时的 ϵ ℓ ϵ_ℓ ϵℓ来得到一个良好的"已条件化"策略， 在此基础上，只在有帮助时采用适中的 β β β设定（例如 β ∈ [ 1.5 , 2.5 ] β∈[1.5,2.5] β∈[1.5,2.5]）。

F. 额外的算法细节

本节详细说明算法1中任务相关参数的设定方式。

Advantage Estimation

优势估计：在后训练阶段，我们使用下式估计优势函数：

A π ( o t , a t ) = ∑ t ′ = t t + N − 1 r t ′ + V π ( o t + N ) − V π ( o t ) , A^\pi(\text{o}t,\text{a}t)=\sum{t'=t}^{t+N-1} r{t'} + V^\pi(\text{o}_{t+N}) - V^\pi(\text{o}_t), Aπ(ot,at)=t′=t∑t+N−1rt′+Vπ(ot+N)−Vπ(ot),

其中， o t + N \text{o}_{t+N} ot+N 是从同一条轨迹中向前 N N N步采样得到的观测。 我们取 N = 50 N=50 N=50作为前视步数来计算该优势。 在预训练阶段，我们将优势估计计算为：

A π ( o t , a t ) = ∑ t ′ = 0 T r t ′ − V π ( o t ) , A^\pi(\text{o}t,\text{a}t)=\sum{t'=0}^{T} r{t'} - V^\pi(\text{o}_t), Aπ(ot,at)=t′=0∑Trt′−Vπ(ot),

即对每个 episode 令 N = T N=T N=T，这会带来方差较高的优势估计。 我们采用这种优势计算方式，是因为在预训练时，只需对价值函数做一次前向推理，就可以在线计算优势值。 实验结果表明，当预训练阶段使用来自多种任务的大量数据时，这种优势估计效果良好。

Advantage conditioning dropout

优势条件化 dropout：在训练过程中，我们以 30% 的概率随机去掉对优势指示器的条件化。 我们采用这种 dropout，是为了在推理时既可以从"带优势条件"的策略采样，也可以从"无条件"的策略采样，并利用 CFG 在测试时进行策略改进（细节见第 E 节）； 而且在效果上，它相当于替代了损失中的权重系数 α α α。

Advantage threshold

优势阈值：各任务的优势阈值 ϵ ℓ ϵ_ℓ ϵℓ按如下方式设定。 在预训练阶段，我们为每个任务选择一个阈值，使得大约 30% 的示范数据的优势为正， 这一比例是基于从该任务中随机抽取 1 万个样本计算得到的。 在微调阶段，我们一般选择阈值，使得每次迭代中大约 40% 的评估 rollouts 拥有正优势。 对于"T 恤和短裤折叠"任务（在该任务上，仅用高质量示范训练得到的策略虽然成功率很高，但动作较慢）， 我们会提高阈值，使得只有大约 10% 的数据具有正优势。

Dataset composition

数据集构成：对于所有任务，我们都采用算法1中描述的数据集聚合策略。 然而，各任务本身具有不同特性：episode 长度不同，第 0 次迭代模型在各任务上的初始表现也不同， 并且其中一个任务（组装纸箱）是在外部部署场景中执行的。 因此，我们在起始示范数据量以及后续迭代中采集的经验数据量上，都为不同任务设定了不同规模。 对于"T 恤与短裤折叠"任务，我们只使用自主评估数据，而不包含专家纠正数据。 随着我们将模型性能优化到与人类专家在速度上非常接近，人工再进行纠正变得非常困难。 在该任务上，我们在 4 个机器人工作站上共采集了 300 个 episode 用于报告评估结果。 对于"多样化折衣"任务，我们采集了 450 个评估 episode 和 287 个纠正 episode。 在"失败模式消除"的消融实验中，我们同时采集自主数据与策略纠正数据。 总计在 3 台机器人上采集了大约 1000 个自主 episode 和 280+378 个纠正 episode。 对于"纸箱组装"任务，我们直接在部署场景中采集数据，每次迭代收集 600 个示范 episode 与 360 个纠正 episode，共使用 3 台机器人。 对于"咖啡制作"任务，我们进行了一次迭代，采集了 429 个纠正 episode 和 414 个自主 episode。