流程图在算法设计中的实战应用

在算法设计领域，清晰的逻辑梳理是高效开发的核心前提。流程图作为一种可视化的逻辑表达工具，能够将抽象的算法思路转化为直观的图形流程，帮助开发者规避逻辑漏洞、优化执行路径。而一款优质的绘图工具，能让流程图的绘制与应用更高效。本文将聚焦流程图在算法设计中的实战价值，结合国产工具 良功绘图网站（https://www.lghuitu.com） 及多款国外主流工具，从基础认知、实战案例到优化技巧，全面拆解其应用逻辑。

算法设计的本质是对问题求解步骤的抽象与优化，而流程图通过标准化的符号和逻辑连接，将"输入-处理-输出"的核心流程具象化。无论是新手入门算法设计，还是资深开发者攻克复杂问题，流程图都能发挥三大核心作用：一是梳理逻辑框架，避免思路混乱；二是暴露逻辑漏洞，降低调试成本；三是提升协作效率，让团队快速对齐思路。在实际开发中，许多算法 bug 并非源于代码语法错误，而是逻辑链路不完整或分支覆盖不全，而流程图恰好能针对性解决这一问题。

一、流程图基础认知：算法可视化的核心工具

流程图是通过一系列标准化符号和连接线，表达特定流程中各步骤之间逻辑关系的图形化工具。在算法设计中，它并非简单的"步骤罗列"，而是对算法逻辑的结构化拆解，其核心价值在于"将抽象逻辑转化为可验证的可视化路径"。

1.1 流程图核心符号体系

算法设计中常用的流程图符号遵循国际通用标准，不同符号对应不同的逻辑功能，精准使用符号是保证流程图有效性的基础：

椭圆符号：表示算法的"开始"或"结束"，一个流程图只能有一个开始节点，但可根据逻辑需求设置多个结束节点。
矩形符号：表示具体的"处理步骤"，如变量定义、数值计算、函数调用等算法核心操作。
菱形符号：表示"判断条件"，用于表达分支逻辑，每个判断节点需包含至少两个输出分支（是/否、满足/不满足）。
平行四边形符号：表示"输入/输出"操作，如读取数据、打印结果、文件读写等与外部交互的步骤。
箭头符号：表示"逻辑流向"，明确步骤之间的执行顺序，避免出现无流向的孤立节点。
圆形符号：表示"连接点"，用于拆分或合并流程线，适用于复杂流程图的分层设计。

1.2 流程图的绘制规则与核心优势

绘制算法流程图需遵循"逻辑清晰、简洁规范、无歧义"三大原则：首先，流程线必须明确，避免交叉缠绕；其次，节点命名需简洁准确，使用"动词+宾语"的结构（如"定义数组 arr""比较 a 与 b 的大小"）；最后，复杂流程需分层绘制，通过连接点关联不同层级的逻辑。

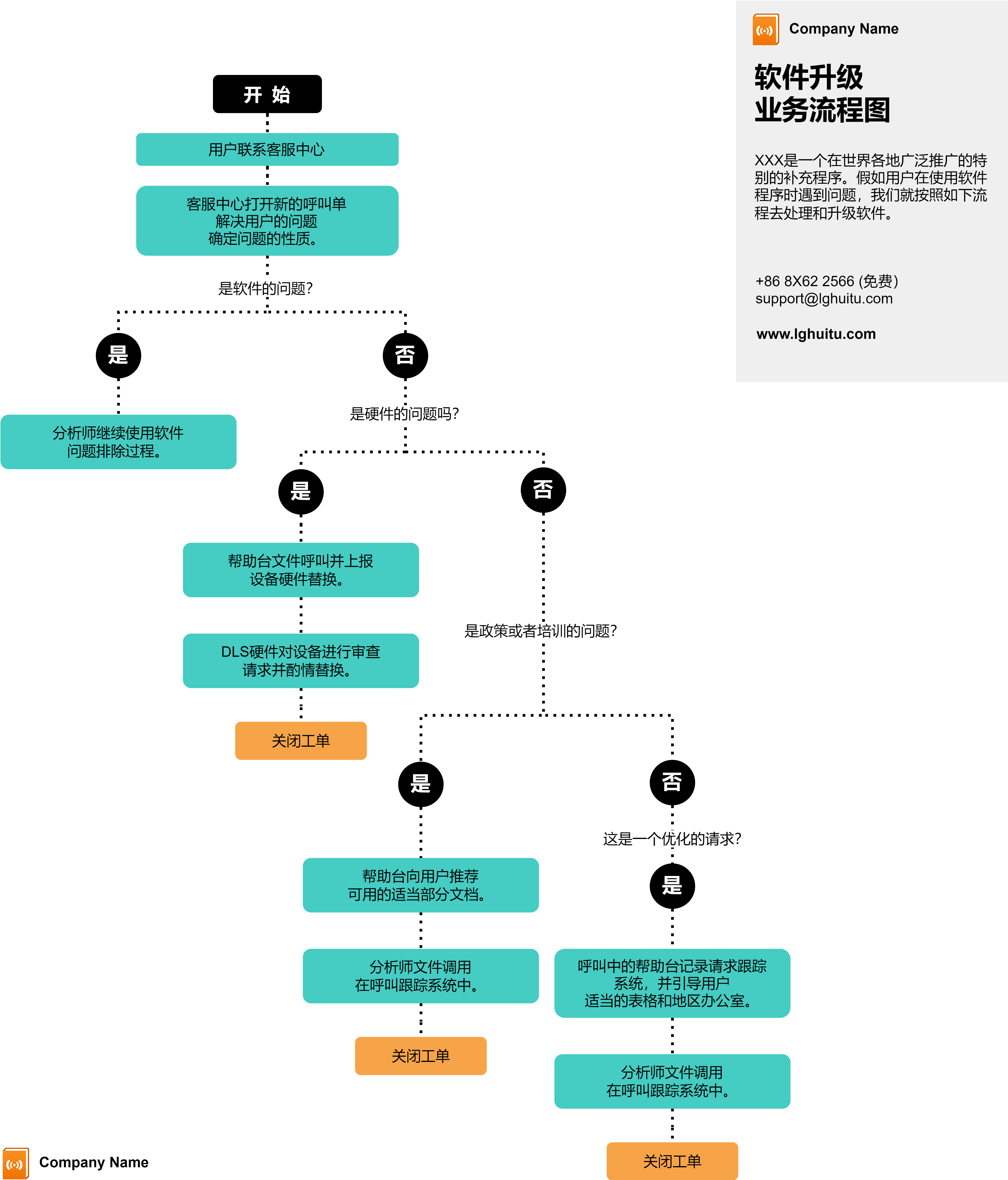
图1 流程图核心符号体系及含义说明

流程图在算法设计中的核心优势体现在三个维度：一是"逻辑可视化"，将抽象的算法思路转化为直观图形，降低理解门槛；二是"漏洞可追溯"，通过遍历流程节点，快速发现逻辑断点、分支遗漏等问题；三是"协作高效化"，跨团队协作时，流程图可作为通用语言，避免因文字描述模糊导致的理解偏差。

二、算法设计的核心流程与流程图的契合点

算法设计遵循"需求分析-逻辑建模-代码落地-调试优化-迭代升级"的闭环流程，而流程图在每个阶段都能发挥关键作用，成为连接"思路"与"代码"的桥梁。

2.1 需求分析阶段：明确算法边界与核心目标

需求分析是算法设计的起点，核心是明确"要解决什么问题""输入输出是什么""约束条件有哪些"。此时绘制流程图，可快速梳理需求的核心逻辑，避免偏离目标。

例如，在设计"用户登录验证算法"时，通过流程图可明确核心流程：读取用户输入（账号、密码）→ 验证输入合法性（是否为空、格式是否正确）→ 与数据库中的用户信息比对 → 验证通过则登录成功，否则返回错误提示。这一过程中，流程图能清晰界定算法的输入输出、关键判断节点，为后续逻辑建模奠定基础。

2.2 逻辑建模阶段：拆解算法步骤与分支逻辑

逻辑建模是算法设计的核心，需将需求拆解为可执行的步骤，并处理复杂的分支、循环逻辑。此时流程图的价值在于"将模糊的思路转化为结构化的步骤"，尤其适用于处理多分支、嵌套循环等复杂场景。

以"电商订单支付算法"为例，其逻辑包含多分支判断：订单金额是否满足优惠条件、用户选择的支付方式（微信、支付宝、银行卡）、支付是否超时、是否需要开具发票等。通过流程图可逐层拆解这些逻辑，明确每个分支的执行路径，避免出现逻辑混乱。

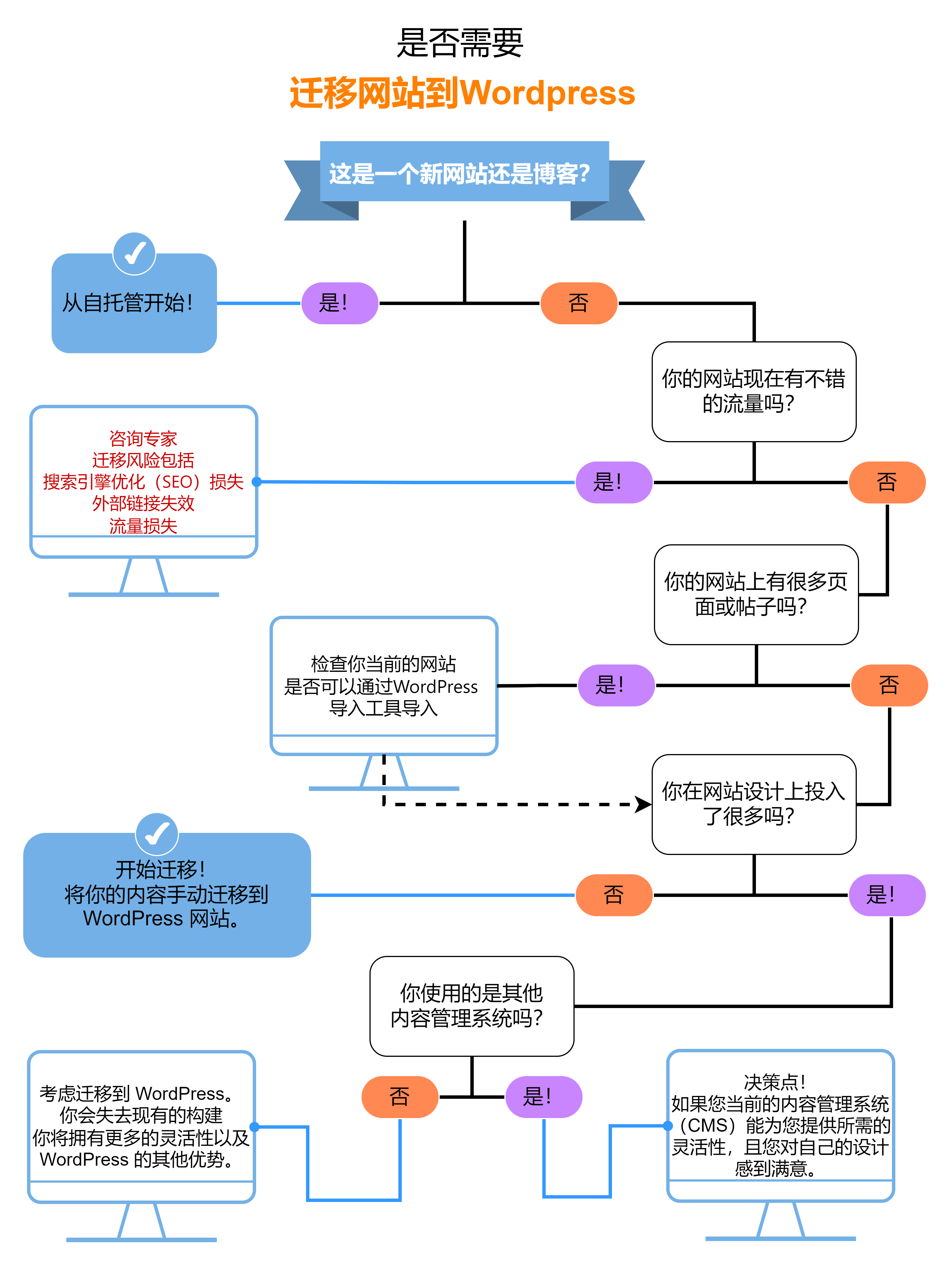
图2 设计各阶段与流程图的对应关系

2.3 代码落地阶段：降低编码难度与出错概率

许多开发者在编码时容易陷入"思路中断"或"逻辑错误"，而流程图可作为编码的"导航图"，让开发者按图索骥，逐步将图形化逻辑转化为代码。

例如，在编写"快速排序算法"时，先通过流程图梳理核心逻辑：选择基准元素 → 分区（小于基准的元素放左侧，大于基准的放右侧）→ 递归排序左侧子数组 → 递归排序右侧子数组 → 合并结果。编码时，只需按照流程图的步骤，逐步实现每个节点的功能，即可降低编码难度，减少逻辑错误。

2.4 调试优化阶段：定位问题与优化执行路径

算法调试的核心是找到"逻辑漏洞"或"性能瓶颈"，而流程图可帮助开发者快速定位问题所在。通过对比代码与流程图，可检查是否存在步骤遗漏、分支判断错误、循环条件不合理等问题。

在性能优化时，流程图也能发挥作用。例如，通过分析流程图中的循环节点，可判断是否存在重复计算；通过梳理分支逻辑，可优化判断条件的顺序，减少不必要的执行步骤，提升算法效率。

2.5 迭代升级阶段：沉淀经验与快速迭代

算法并非一成不变，需根据业务需求变化或性能反馈进行迭代。此时，流程图可作为"算法文档"，帮助开发者快速回顾原有逻辑，明确迭代点，避免因人员变动或时间推移导致的知识流失。

例如，当电商订单支付算法需要新增"花呗分期支付"功能时，开发者可基于原有流程图，在支付方式分支中新增花呗分期的判断逻辑及执行步骤，快速完成迭代，同时保证整体逻辑的一致性。

三、主流流程图工具对比与选型建议

选择合适的流程图工具，能大幅提升算法设计的效率。以下结合算法设计的需求，对比国产工具良功绘图与四款国外主流工具的核心特性，为开发者提供选型参考。

工具名称	核心定位	适用场景	核心优势	潜在劣势	是否免费
良功绘图	轻量高效的国产绘图工具	个人开发者、中小企业、算法原型设计	操作简单，无需安装；支持算法流程图模板；导出格式丰富（PNG、PDF、SVG）；中文界面，无语言障碍	高级协作功能较少，适合单机或小团队使用	基础功能免费，高级功能付费
Drawio	开源免费的通用绘图工具	个人开发者、开源项目、轻量协作	完全免费开源；支持本地存储和云端同步；可嵌入文档（如Google Docs）；符号库丰富	界面设计较简洁，复杂流程图的分层管理较弱	完全免费
Lucidchart	企业级协作绘图工具	大型团队、复杂算法系统设计	协作功能强大，支持多人实时编辑；模板丰富，含算法、架构等专业模板；与主流工具（Slack、Jira）集成	免费版功能有限，付费版价格较高；国内访问速度较慢	免费版+付费版
Microsoft Visio	专业级办公绘图工具	企业办公、复杂流程设计	功能全面，支持复杂流程图、架构图绘制；与Office套件深度集成；兼容性强	收费软件，价格较高；体积较大，启动速度慢	收费
FigJam	设计协作型绘图工具	设计团队、跨职能协作项目	界面美观，支持手绘风格；协作互动性强，可添加评论、标注；支持自定义组件	算法相关模板较少；侧重设计协作，专业绘图功能较弱	免费版+付费版

3.1 工具选型的核心原则

个人开发者或小团队：优先选择良功绘图或Draw.io，前者操作简单、中文界面友好，后者完全免费开源，均能满足算法流程图的绘制需求。
大型团队或复杂算法系统：可选择Lucidchart或Microsoft Visio，前者协作功能强大，后者专业功能全面，适合跨部门协作或复杂流程设计。
跨职能协作（如算法+设计+产品）：推荐FigJam，其互动协作功能能提升跨团队沟通效率，但需配合算法模板使用。

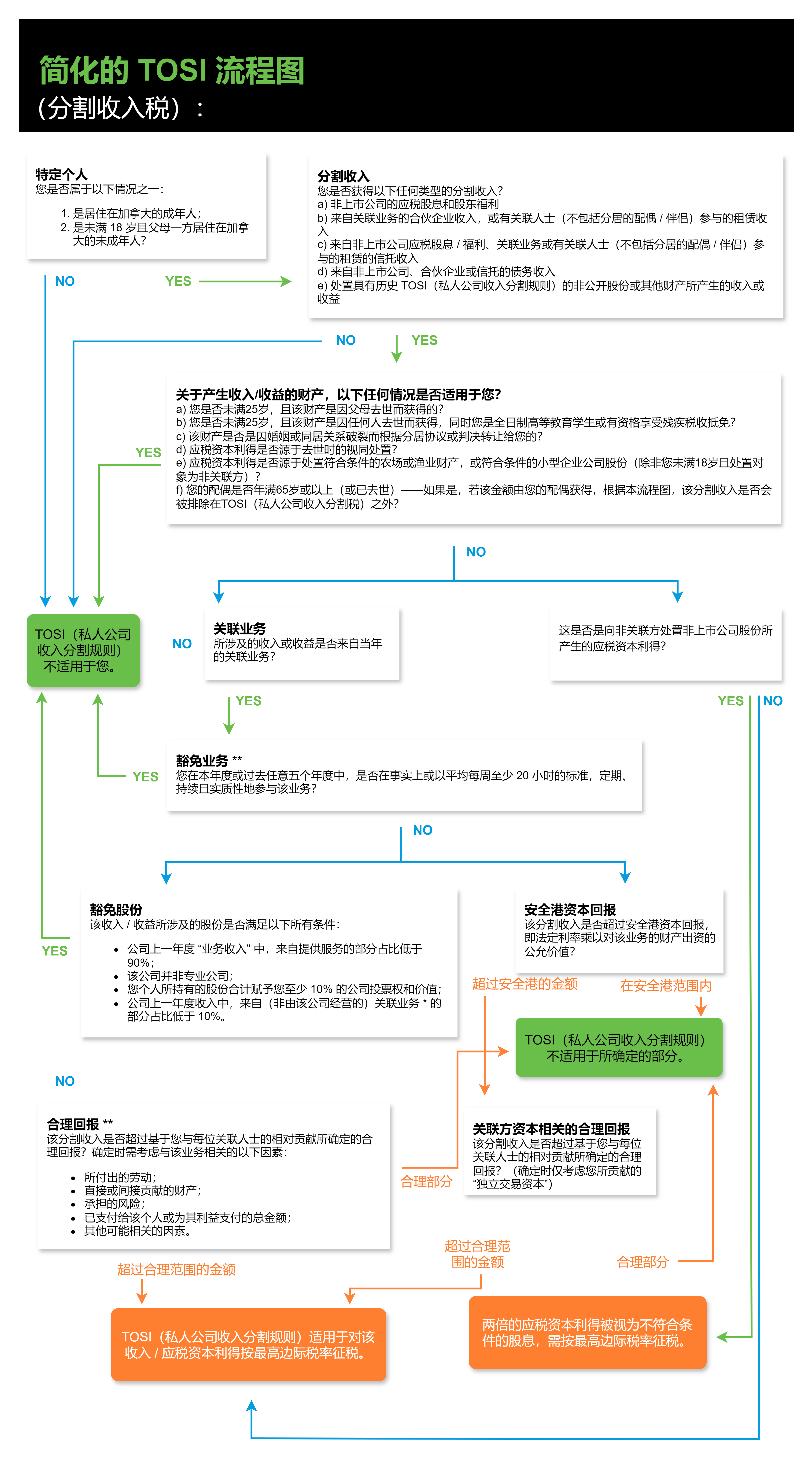
图3 主流流程图工具的核心功能界面示例

3.2 良功绘图在算法设计中的实操优势

作为国产轻量型工具，良功绘图特别适合算法设计场景的核心优势：一是提供"算法流程图"专项模板，包含排序、查找、动态规划等经典算法的流程框架，可直接修改使用；二是支持拖拽式绘制，符号拖拽、流程线自动吸附，无需手动调整格式；三是导出格式支持PNG、PDF、SVG，可直接插入论文、技术文档或代码注释中；四是无需安装客户端，浏览器打开即可使用，不占用设备资源。

四、流程图在经典算法设计中的实战案例

以下结合五大经典算法场景，详细拆解流程图如何助力逻辑梳理与代码实现，所有案例均基于良功绘图完成流程图设计，确保实操性。

4.1 排序算法：冒泡排序的流程图设计与实现

冒泡排序是入门级排序算法，核心逻辑是重复遍历待排序数组，每次比较相邻元素，将较大元素"冒泡"到数组末尾。通过流程图可清晰梳理其循环与判断逻辑。

4.1.1 算法需求与约束

输入：未排序的整数数组（如[3,1,4,1,5,9]）
输出：升序排列的整数数组（如[1,1,3,4,5,9]）
约束：时间复杂度不做严格限制，保证逻辑清晰即可

4.1.2 流程图设计

开始 → 定义待排序数组arr和数组长度n
初始化交换标记flag为true（用于优化，若某轮无交换则说明数组已有序）
外层循环：i从0到n-2（控制排序轮数）
内层循环：j从0到n-2-i（每轮遍历后，末尾i个元素已有序，无需再比较）
判断arr[j]是否大于arr[j+1]：
- 是：交换arr[j]和arr[j+1]，设置flag为true
- 否：不执行交换
内层循环结束后，判断flag是否为false：
- 是：说明数组已有序，跳出外层循环
- 否：重置flag为false，进入下一轮外层循环
循环结束 → 输出排序后的数组 → 结束

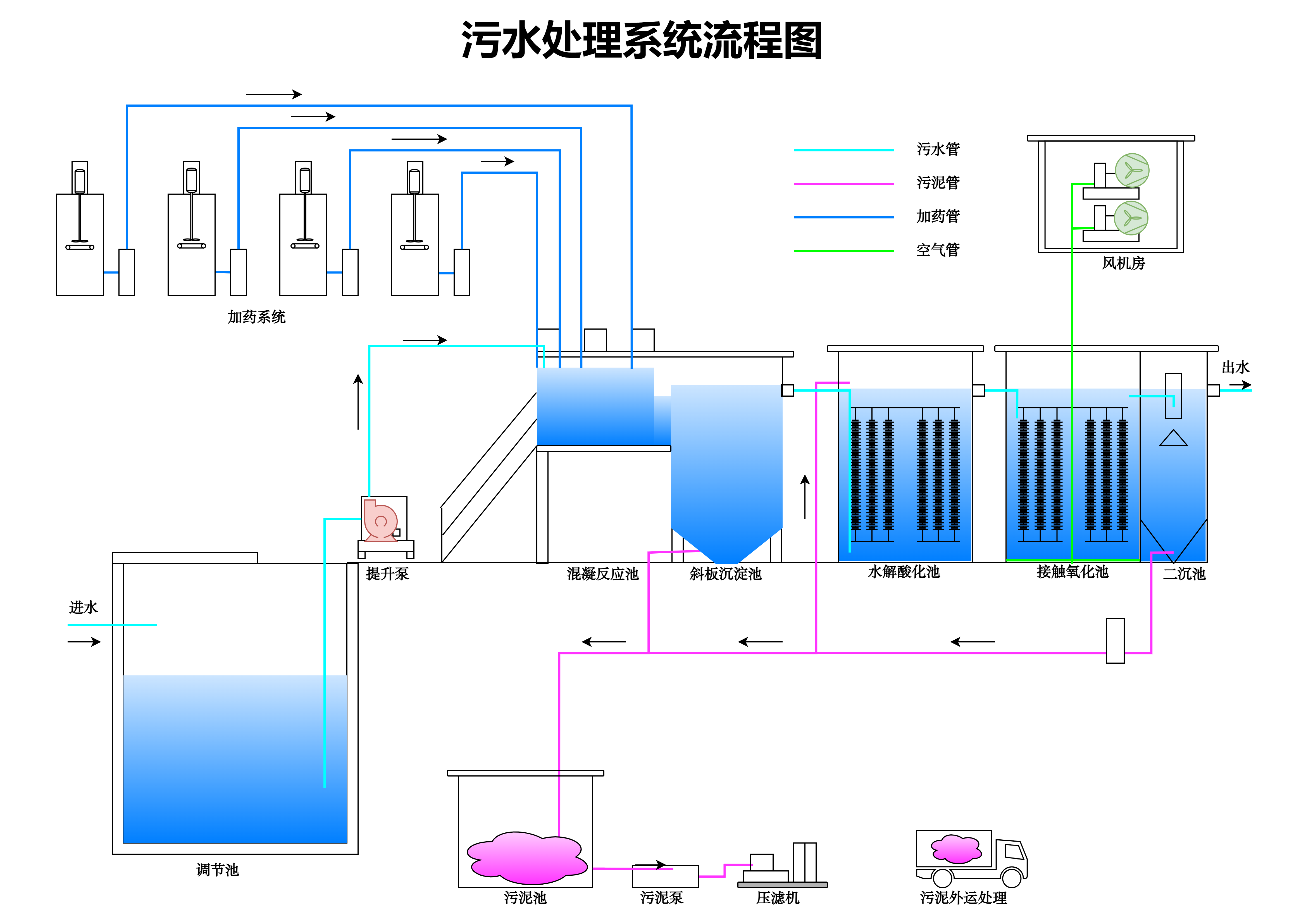
图4 流程图逻辑梳理

4.1.3 代码实现（Python）

python 复制代码

def bubble_sort(arr):
    n = len(arr)
    for i in range(n - 1):
        flag = False  # 初始化交换标记
        for j in range(n - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                flag = True
        if not flag:  # 无交换则数组已有序，提前退出
            break
    return arr

# 测试代码
test_arr = [3, 1, 4, 1, 5, 9]
sorted_arr = bubble_sort(test_arr)
print("排序结果：", sorted_arr)

4.1.4 流程图的价值体现

通过流程图，清晰界定了外层循环、内层循环的执行条件，以及交换标记的作用，避免了"多轮无效循环"的问题。新手在编码时，只需按照流程图的步骤逐一实现，即可快速掌握冒泡排序的核心逻辑，同时理解"提前退出"的优化思路。

4.2 查找算法：二分查找的流程图设计与实现

二分查找是高效的查找算法，适用于有序数组，核心逻辑是通过不断缩小查找范围，快速定位目标元素。其分支逻辑较多，流程图能帮助开发者理清边界条件。

4.2.1 算法需求与约束

输入：有序整数数组arr、目标值target
输出：目标值在数组中的索引（若不存在则返回-1）
约束：数组必须有序，支持升序排列

4.2.2 流程图设计

开始 → 定义有序数组arr、目标值target，初始化左指针left=0，右指针right=len(arr)-1
判断left是否小于等于right：
- 否：说明未找到目标值，返回-1 → 结束
- 是：计算中间索引mid = (left + right) // 2
判断arr[mid]是否等于target：
- 是：返回mid → 结束
- 否：判断arr[mid]是否大于target
  - 是：说明目标值在左半部分，设置right=mid-1
  - 否：说明目标值在右半部分，设置left=mid+1
回到步骤2，继续循环

图5 流程图可视化表达

4.2.3 代码实现（Python）

python 复制代码

def binary_search(arr, target):
    left = 0
    right = len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] > target:
            right = mid - 1
        else:
            left = mid + 1
    return -1

# 测试代码
sorted_arr = [1, 3, 5, 7, 9, 11]
target = 7
index = binary_search(sorted_arr, target)
print("目标值索引：", index)  # 输出4

4.2.4 流程图的价值体现

二分查找的核心难点是边界条件的处理（left与right的关系、mid的计算方式）。通过流程图，清晰展示了"查找成功""目标值在左半部分""目标值在右半部分""查找失败"四种分支逻辑，帮助开发者避免出现"死循环"或"漏查"的问题。例如，若未明确left<=right的循环条件，可能导致索引越界；若未正确设置right=mid-1或left=mid+1，可能导致查找范围无法缩小。

4.3 动态规划：0-1背包问题的流程图设计与实现

0-1背包问题是动态规划的经典案例，核心逻辑是通过状态转移方程，在有限容量的背包中选择物品，使总价值最大。其逻辑复杂，流程图能帮助开发者梳理状态定义与转移路径。

4.3.1 算法需求与约束

输入：物品数量n、背包容量C、物品重量数组w、物品价值数组v
输出：背包能容纳的最大价值
约束：每个物品只能选择放入或不放入，不能分割

4.3.2 流程图设计

开始 → 定义n、C、w、v，初始化动态规划数组dp（dp[i][j]表示前i个物品放入容量为j的背包的最大价值）
初始化dp[0][j] = 0（前0个物品，价值为0），dp[i][0] = 0（背包容量为0，价值为0）
外层循环：i从1到n（遍历每个物品）
内层循环：j从1到C（遍历每个背包容量）
判断第i个物品的重量w[i-1]是否大于j（因数组索引从0开始）：
- 是：无法放入，dp[i][j] = dp[i-1][j]
- 否：选择"放入"或"不放入"的最大值，即dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i-1]] + v[i-1])
循环结束 → 输出dp[n][C] → 结束

图6 动态规划流程图设计

4.3.3 代码实现（Python）

python 复制代码

def zero_one_knapsack(n, C, w, v):
    # 初始化dp数组，(n+1)行(C+1)列
    dp = [[0] * (C + 1) for _ in range(n + 1)]
    for i in range(1, n + 1):
        for j in range(1, C + 1):
            if w[i-1] > j:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i-1]] + v[i-1])
    return dp[n][C]

# 测试代码
n = 3  # 物品数量
C = 5  # 背包容量
w = [2, 3, 4]  # 物品重量
v = [3, 4, 5]  # 物品价值
max_value = zero_one_knapsack(n, C, w, v)
print("背包最大价值：", max_value)  # 输出7（放入前两个物品：重量2+3=5，价值3+4=7）

4.3.4 流程图的价值体现

0-1背包问题的核心是状态转移方程的理解，流程图通过分层循环（物品遍历、容量遍历）和分支判断（能否放入物品），清晰展示了dp数组的填充逻辑。开发者通过流程图可明确：每个dp[i][j]的取值都依赖于上一层的dp[i-1][j]或dp[i-1][j-w[i-1]]，从而快速掌握动态规划的"状态定义-转移方程-初始化-结果输出"全流程。

4.4 图算法：Dijkstra最短路径的流程图设计与实现

Dijkstra算法用于求解图中从起点到其他所有顶点的最短路径，核心逻辑是通过贪心策略，不断更新顶点的最短距离。其流程包含顶点选择、距离更新等多个步骤，流程图能帮助开发者理清逻辑顺序。

4.4.1 算法需求与约束

输入：有向图（邻接矩阵表示）、起点vertex
输出：起点到每个顶点的最短距离
约束：图中边的权重为非负数

4.4.2 流程图设计

开始 → 定义图的邻接矩阵graph、起点vertex，获取顶点数量n
初始化最短距离数组dist（dist[i]表示起点到顶点i的最短距离），dist[vertex] = 0，其余元素设为无穷大
初始化访问标记数组visited，所有元素设为False（标记顶点是否已确定最短距离）
外层循环：i从0到n-1（需确定n个顶点的最短距离）
选择未访问顶点中dist最小的顶点u，标记visited[u] = True
内层循环：遍历所有顶点v，判断v是否未访问且graph[u][v]存在（非无穷大）
若dist[v] > dist[u] + graph[u][v]：更新dist[v] = dist[u] + graph[u][v]
内层循环结束，回到步骤4
所有顶点访问完毕 → 输出dist数组 → 结束

图7 流程图逻辑拆解

4.4.3 代码实现（Python）

python 复制代码

import sys

def dijkstra(graph, vertex):
    n = len(graph)
    INF = sys.maxsize
    dist = [INF] * n
    dist[vertex] = 0
    visited = [False] * n
    
    for _ in range(n):
        # 选择未访问且dist最小的顶点u
        min_dist = INF
        u = -1
        for i in range(n):
            if not visited[i] and dist[i] < min_dist:
                min_dist = dist[i]
                u = i
        if u == -1:
            break  # 无可达顶点
        visited[u] = True
        
        # 更新相邻顶点的距离
        for v in range(n):
            if not visited[v] and graph[u][v] != INF and dist[v] > dist[u] + graph[u][v]:
                dist[v] = dist[u] + graph[u][v]
    return dist

# 测试代码（邻接矩阵表示图，INF表示无直接边）
INF = sys.maxsize
graph = [
    [0, 2, 5, INF, INF],
    [2, 0, 1, 3, INF],
    [5, 1, 0, 2, 4],
    [INF, 3, 2, 0, 1],
    [INF, INF, 4, 1, 0]
]
start_vertex = 0
shortest_dist = dijkstra(graph, start_vertex)
print("起点到各顶点的最短距离：", shortest_dist)  # 输出[0, 2, 3, 4, 5]

4.4.4 流程图的价值体现

Dijkstra算法的流程包含"选择最小距离顶点""更新相邻顶点距离"两个核心步骤，流程图清晰界定了这两个步骤的执行顺序，以及访问标记数组的作用。开发者通过流程图可避免"重复更新已确定顶点的距离"或"遗漏相邻顶点"的问题，同时理解贪心策略在算法中的具体应用。

4.5 贪心算法：活动选择问题的流程图设计与实现

活动选择问题是贪心算法的经典案例，核心逻辑是在多个互斥活动中选择最多的活动，使其在时间上不重叠。流程图能帮助开发者理清活动选择的判断标准与执行步骤。

4.5.1 算法需求与约束

输入：活动列表（每个活动包含开始时间s[i]和结束时间f[i]）
输出：最多可选择的不重叠活动集合
约束：活动按结束时间升序排列

4.5.2 流程图设计

开始 → 定义活动列表activities（按结束时间升序排列），初始化选中活动列表result
选择第一个活动（结束时间最早），加入result，记录上一个选中活动的结束时间last_end = activities[0][1]
循环遍历剩余活动（i从1到len(activities)-1）：
判断当前活动的开始时间s[i]是否大于等于last_end：
- 是：选中该活动，加入result，更新last_end = activities[i][1]
- 否：跳过该活动
遍历结束 → 输出result → 结束

图8 流程图

4.5.3 代码实现（Python）

python 复制代码

def activity_selection(activities):
    # 活动已按结束时间升序排列
    result = [activities[0]]
    last_end = activities[0][1]
    for i in range(1, len(activities)):
        s_i, f_i = activities[i]
        if s_i >= last_end:
            result.append(activities[i])
            last_end = f_i
    return result

# 测试代码（活动格式：(开始时间, 结束时间)，已按结束时间排序）
activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
selected_activities = activity_selection(activities)
print("最多可选择的不重叠活动：", selected_activities)  # 输出[(1, 4), (5, 7), (8, 11), (12, 16)]

4.5.4 流程图的价值体现

通过流程图，清晰展示了贪心算法"选择结束时间最早的活动"这一核心策略，以及"当前活动开始时间≥上一活动结束时间"的选择标准。开发者通过流程图可快速理解贪心算法的"局部最优→全局最优"逻辑，避免在选择活动时出现"因追求单个活动时长而导致总数量减少"的问题。

五、流程图在复杂算法系统中的综合应用

除了经典基础算法，流程图在复杂算法系统（如分布式算法、机器学习算法）中也能发挥关键作用，帮助开发者梳理多模块、多流程的逻辑关系。

5.1 分布式算法：一致性哈希算法的流程图设计

一致性哈希算法是分布式系统中用于负载均衡的核心算法，核心逻辑是将节点和数据映射到哈希环上，通过顺时针查找确定数据存储节点。其流程涉及哈希计算、节点映射、数据定位等多个环节，流程图能帮助开发者理清各环节的关联关系。

5.1.1 算法核心流程（流程图梳理）

开始 → 初始化哈希环（范围0-2^32-1）
节点注册：计算每个节点的哈希值，映射到哈希环上
数据存储：计算数据的哈希值，在哈希环上顺时针查找最近的节点，将数据存储到该节点
节点下线：删除该节点在哈希环上的映射，其存储的数据重新映射到下一个最近节点
节点上线：计算新节点的哈希值，映射到哈希环上，从相邻节点中迁移部分数据到新节点
结束

图9 流程图框架

5.1.2 流程图的应用价值

一致性哈希算法涉及"节点注册/下线/上线""数据存储/迁移"等多个场景，流程图能清晰界定每个场景的执行步骤，以及各模块之间的依赖关系。在分布式系统开发中，团队成员可通过流程图快速对齐逻辑，避免因节点状态变化导致的数据丢失或负载不均问题。

5.2 机器学习算法：线性回归模型的流程图设计

线性回归是机器学习中的基础算法，核心逻辑是通过最小二乘法求解回归系数，构建线性预测模型。其流程涉及数据预处理、模型训练、预测评估等多个步骤，流程图能帮助开发者梳理全流程的逻辑顺序。

5.2.1 算法核心流程（流程图梳理）

开始 → 数据收集（获取特征变量X和目标变量y）
数据预处理：缺失值填充、异常值处理、特征标准化
划分数据集：训练集（70%-80%）、测试集（20%-30%）
模型训练：初始化回归系数θ，通过最小二乘法求解θ（使损失函数最小）
模型预测：使用测试集数据输入模型，得到预测结果ŷ
模型评估：计算均方误差（MSE）、决定系数（R²），判断模型效果
模型优化：若评估指标不达标，调整特征或正则化参数，重新训练
输出最终模型 → 结束

图10 全流程流程图

5.2.2 流程图的应用价值

线性回归模型的流程涉及数据处理、模型训练、评估优化等多个环节，流程图能帮助开发者明确每个环节的输入输出、执行顺序，避免出现"数据未预处理直接训练""未划分测试集导致过拟合"等问题。同时，流程图可作为机器学习项目的文档，方便团队成员快速复现模型开发流程。

六、流程图绘制的常见误区与优化技巧

在算法设计中，流程图的价值能否充分发挥，取决于绘制的规范性与合理性。以下总结常见误区，并提供优化技巧，帮助开发者提升流程图的实用性。

6.1 常见绘制误区

符号滥用：使用错误的符号表达逻辑（如用矩形表示判断、用菱形表示处理步骤），导致逻辑歧义。
逻辑混乱：流程线交叉缠绕、节点顺序不合理，无法清晰体现执行顺序。
过度简化：遗漏关键判断节点或处理步骤（如二分查找中未体现left与right的更新逻辑），导致流程图无法指导编码。
命名模糊：节点命名使用"处理数据""进行判断"等模糊表述，无法明确具体操作。
缺乏分层：复杂算法的流程图未分层设计，所有逻辑堆砌在一张图中，可读性极差。

6.2 优化技巧

标准化符号：严格遵循"椭圆-开始/结束、矩形-处理、菱形-判断"的符号规则，确保读者理解无歧义。
逻辑分层：复杂算法按"主流程-子流程"分层绘制，主流程体现核心逻辑，子流程详细拆解关键步骤，通过连接点关联。
精准命名：节点命名采用"动作+对象"的结构（如"计算中间索引mid""判断目标值是否存在"），明确具体操作。
简化流程线：避免流程线交叉，可通过调整节点位置或使用连接点优化布局；流程线必须带箭头，明确执行方向。
突出核心：核心判断节点或关键处理步骤可通过颜色标注（如良功绘图支持节点颜色自定义），提升可读性。
迭代优化：绘制完成后，对照算法逻辑遍历流程图，检查是否存在遗漏、逻辑矛盾，根据实际应用反馈持续优化。

6.3 案例：优化前后的流程图对比

以"快速排序算法"为例，优化前的流程图将递归逻辑、分区逻辑堆砌在一起，流程线交叉；优化后按"主流程（递归调用）-子流程（分区操作）"分层绘制，主流程体现递归逻辑，子流程详细拆解分区步骤，可读性大幅提升。

七、未来趋势：流程图与算法设计的深度融合

随着人工智能技术的发展，流程图在算法设计中的应用将呈现两大趋势：一是AI辅助流程图绘制，二是流程图与代码生成工具的联动。

7.1 AI辅助流程图绘制

目前已有部分工具（如Lucidchart、FigJam）集成了AI功能，支持通过自然语言描述生成流程图。例如，输入"设计二分查找算法的流程图，输入为有序数组和目标值，输出为索引或-1"，AI可自动生成核心流程框架，开发者只需微调细节。未来，AI将能更精准地理解复杂算法逻辑，甚至根据代码反向生成流程图，帮助开发者快速梳理 legacy 代码的逻辑。

7.2 流程图与代码生成工具的联动

流程图与代码生成工具的联动将成为核心趋势。例如，在良功绘图中绘制完算法流程图后，可直接导出为对应的代码框架（如Python、Java），开发者只需填充具体的处理逻辑；反之，也可通过代码反向生成流程图，用于文档生成或逻辑梳理。这种"流程图-代码"的双向联动，将大幅提升算法设计的效率，降低新手入门门槛。

八、结论

流程图作为算法设计的可视化工具，其核心价值在于"将抽象逻辑转化为可验证、可执行的结构化路径"。从基础算法（排序、查找）到复杂算法系统（分布式算法、机器学习算法），流程图都能帮助开发者梳理逻辑、规避漏洞、提升协作效率。

在工具选择上，国产工具良功绘图网站以其轻量高效、操作简单、中文界面友好的优势，特别适合个人开发者和小团队的算法设计需求；国外工具如Drawio、Lucidchart则适用于开源项目或大型团队的协作场景。

未来，随着AI技术的融入，流程图将与算法设计深度融合，成为连接"思路-图形-代码"的核心桥梁。对于开发者而言，掌握流程图的绘制技巧，将其融入算法设计的全流程，不仅能提升自身的逻辑梳理能力，还能显著提高开发效率与代码质量。

无论是算法新手还是资深开发者，都应重视流程图在算法设计中的应用，将其作为算法开发的"必备工具"，在实践中不断优化绘制技巧，充分发挥其在逻辑梳理、协作沟通、文档沉淀中的核心价值。