「干货长文」强化学习完全指南：从基础MDP到TRPO/PPO/GRPO算法演进

随着 gpt-o1出现以及 DeepSeek-R1 的技术开源，强化学习从以谷歌 DeepMind 团队为主的游戏领域，以及与传统控制相结合的具身智能机器人领域，走上了LLM甚至多模态的行业赛道。通过复杂任务拆解和奖励为导向的迭代训练大幅提升了大模型解决复杂问题能力，泛化性以及动态调整能力。Reinforce Learning 带领 LLM 步入 2.0 时代，继 PPO 之后，最近关于梯度优化（Policy Optimization）算法的创新也是层出不穷，GRPO，DAPO，CISPO 等但是复杂的数学公式及其底层原理，却让人望而却步；因为强化学习是非常系统性的技术，是从最开始的马尔可夫决策过程 (MDP)，贝尔曼方程，通过其数学性质，使用映射压缩定理逐渐演变而来所以想深刻了解 LLM 中各种变种策略梯度算法的作用与本质，我们需要先了解强化学习的基础，接下来就让我一步一步捋清其来龙去脉

强化学习有两个很重要的性质：一阶马尔可夫性和不动点定理这两点是整个强化学习框架的基石，缺一不可

Infrastructure

Foundation

强化学习的目标是寻找最优策略解决问题于是把智能体 agent 解决实际问题的过程，抽象成马尔可夫决策过程 MDP 该过程具有一阶马尔可夫性：

P(st+1|st,st−1,...,s1)=P(st+1|st)

也就是序列 t+1 的状态只与 t 有关（简化模型，减少计算量）

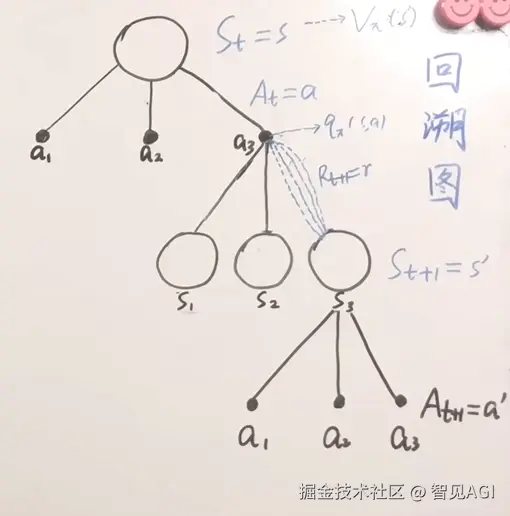
该系统具有五个变量（策略Policy，状态state，行为action，环境environment，奖励reward）目标转化成在特定环境中，选择最优策略，在不同状态下执行最优行动，从而获得最大奖励，完成任务

奖励信号：短期收益价值函数：长期收益，更有远见的判断

通过这种系统的构建形式，我们可以在尽可能短期获得奖励达成目标的同时，又具有一定的前瞻性，通过 Exploration 有一定概率得到更优解

2.贝尔曼方程

2.1 Bellman Expectation Equation

要具有更高时效性，在更短时间内完成任务，于是引入折扣因子γ，引出了强化学习核心数学工具贝尔曼公式该公式描述了给定策略

π下，状态价值函数

Vπ(s)和动作价值函数

Qπ(s,a)的递归关系

Vπ(s)=∑aπ(a∣s)Qπ(s,a)=∑aπ(a∣s)∑s′P(s′∣s,a)[r+γVπ(s′)]Qπ(s,a)=∑s′P(s′∣s,a)[r+v(s′)]=∑s′P(s′∣s,a)[r+γ∑a′π(a′∣s′)Qπ(s′,a′)]

2.2 Bellman Optimal Equation

我们的目标是找到最优策略

π∗，使得价值函数值最大，引出了贝尔曼最优公式

V∗(s)=maxa∑s′P(s′∣s,a)[r+γV∗(s′)]Q∗(s,a)=∑s′P(s′∣s,a)[r+γmaxa′Q∗(s′,a′)]

矩阵形式下等价于求

v=maxπrπ+γPπv

因为折扣因子γ<1，

f(v)=maxπrπ+γPπv=v

符合压缩映射定理 contract mapping theory

|f(v1)−f(v2)|<γ|v1−v2|

可以通过迭代法

vk+1=f(vk)

求解，最终会收敛于唯一解

v∗和得到最优策略

π∗（

π∗不一定唯一）最终

v∗=f(v∗)

得到贝尔曼最优公式

Value-based method

3.Dynamic Proramming

在完全已知环境中（已知迷宫），可以通过动态规划的算法（值迭代和 (截断) 策略迭代）也是 model-based 的强化学习，求贝尔曼最优方程，得到最优策略π∗

策略迭代： Policy evaluation vπk=rπk+γPπkvπk
根据 r 和环境的状态转移矩阵 P 迭代逼近真实的 Vπ(s)

Policy improvement

vπk+1=\argmaxπ(rπ+γPπvπk)

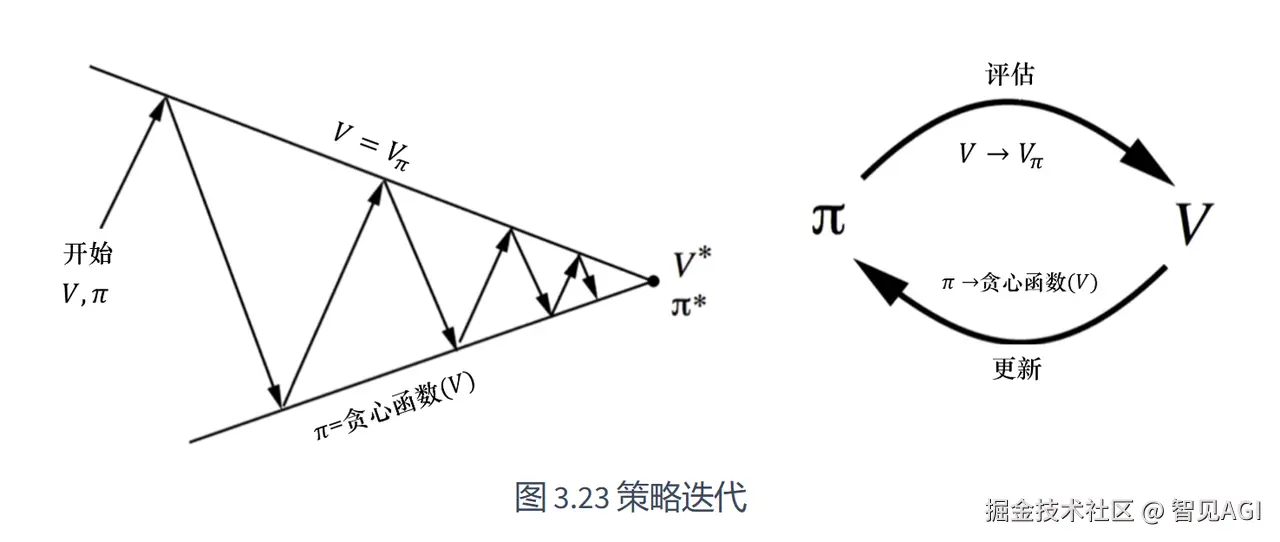
因为映射压缩定律，可以使用自举法，让价值函数

vπ

不断迭代逼近最优解

v∗

，从而得到相对应地最优策略

π∗

4.Monte Carlo

有模型的时候我们可以使用，动态规划方法。但是在无模型的情况下，我们需要采用大数定律，通过蒙特卡罗方法去采样近似其模型

根据 DP 的策略评估和策略改进可知：

{evaluation:vπk=rπk+γPπkvπkimprovement:πk+1=\argmaxπ(rπ+γPπvπk)

πk+1(a|s)=\argmaxπ∑aπ(a|s)qπk(s,a)

无模型的时候，根据大数定律，用采样频率近似概率，对

qπk(s,a)

做近似

qπk(s,a)=E[Gt|St=s,At=a]≈1N∑i=1Ng(i)(s,a)

∴πk+1(a|s)=\argmaxπ∑aπ(a|s)1N∑i=1Ng(i)(s,a)

5.Temporal Difference

但在大多数实际场景中，环境十分复杂不可知，所以需要agent不断去跟环境做交互，采样数据样本来学习这类统称 free-model 无模型强化学习，包括基于时序差分 TD 的 Sarsa 和 Q-learning算法，运用蒙特卡洛概率估计的思想，近似值函数

时序差分 TD 结合了 MC 抽样和动态规划的自举 MC：

V(st)=V(st)+α(Gt−V(st))=V(st)=V(st)+α(rt+1+γ2rt+2+...+γT−t+2rT−V(st))

一步时序差分：

V(st)=V(st)+α(rt+1+γV(st+1)−V(st))

(一步更新，更新频率更快，延迟更低)

V(st)=α(Rt+1+γV(st+1))+(1−α)V(st)

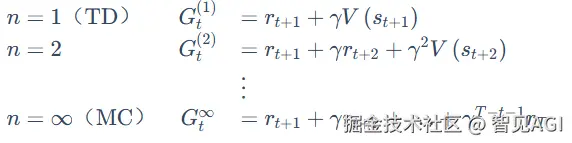
5.1 SARSA

在线 / 同轨策略 (on-policy) TD，SARSA 算法(s->a->r->s->a)，与环境交互得到奖励，不断更新 Q 值来优化策略用一些样本来评估策略，然后更新策略了，策略提升可以在策略未完全评估的情况进行，是广义策略迭代

Q(s,a)=Q(s,a)+α[Rt+1+γQ(s′,a′)−Q(s,a)]

td_error = r + gamma * Q_table[s1, a1] - Q_table[s0, a0] Q_table[s0, a0] += alpha * td_error

SARSA 具体算法如下:

5.2 多步 SARSA

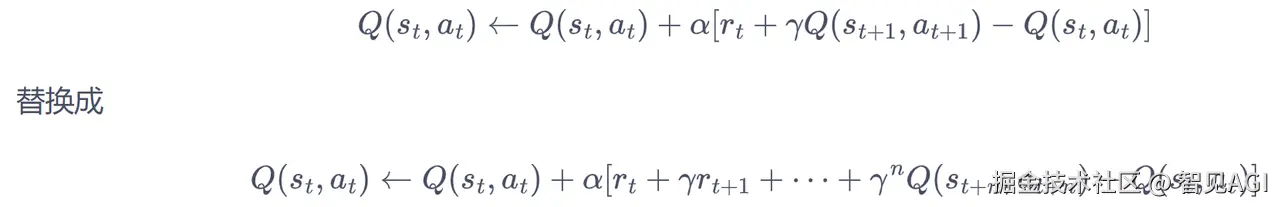
5.3 Q-learning

与 SARSA 不同，是离线/离轨策略 (off-policy) TD 控制在

时刻选择目标策略，得到

Qπ(s,a),st+1

，但是在

st+1

时，执行

at+1

，根据最大 Q 值，选择行动策略

b=argmaxQ(st+1,a)

于是有

Q(s,a)=Q(s,a)+α[Rt+1+γmaxQ(s′,a)−Q(s,a)]

Q 学习在更新 Q 表格的时候所用到的 Q(s′,a′) 对应的动作不一定是下一步会执行的动作，因为下一步实际会执行的动作可能是因为进一步的探索而得到的 Q 学习默认的动作不是通过行为策略来选取的，它默认 a′ 为最佳策略对应的动作，所以 Q 学习算法在更新的时候，不需要传入 a′

5.4 期望 SARSA

不执行

at+1

，根据 Q-table 计算，使用同轨策略

Eπ[Q(st+1|a)|st+1]=∑aπ(a|st+1)Q(st+1,a)

有

Q(s,a)=Q(s,a)+α[r+γEπ[Q(s′|a)|s′]−Q(s,a)]

对比一下 SARSA

Q(s,a)=Q(s,a)+α[Rt+1+γQ(s′,a′)−Q(s,a)]

td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]

Q-learning

Q(s,a)=Q(s,a)+α[Rt+1+γmaxQ(s′,a)−Q(s,a)]

td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]

期望 SARSA

Q(s,a)=Q(s,a)+α[r+γEπ[Q(s′|a)|s′]−Q(s,a)]

Q-learning 是期望 SARSA 的特例，即

Eπ[Q(s′|a)|s′]=maxQ(s′,a∗)

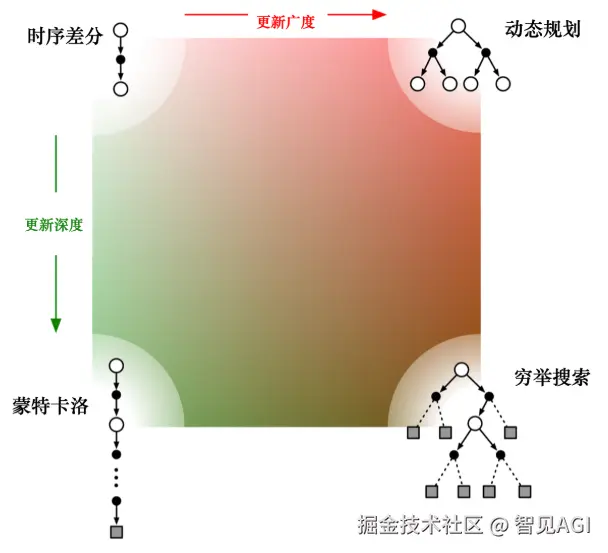
6.动态规划，蒙特卡洛，时序差分的对比

动态规划直接计算期望，它把所有相关的状态都进行加和

蒙特卡洛在当前状态下，采取一条支路，在这条路径上进行更新，更新这条路径上的所有状态

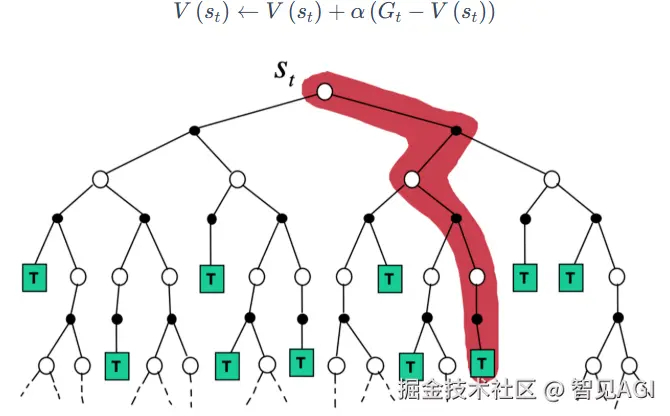
时序差分从当前状态开始，往前走了一步，关注的是非常局部的步骤

强化学习的统一视角

Policy-based method

Value-based method 不适用场景：

随机策略
连续动作空间

7.REINFORCE

除了前面value-based 基于值函数的方法外，还有 policy-based 基于策略的方法策略梯度算法 REINFORCE 求梯度

梯度上升

θt+1=θt+αGt∇log⁡π(At|St;θt)

MC 采样 -> 方差大 BaseLine

∝∑s∈Sμ(s)∑a(qπ(s,a)−b(s))∇π(a|s)

REINFORCE with Baseline b(s) 为基线，减少方差

∑ab(s)∇π(a|s)=b(s)∇∑aπ(a|s)=b(s)∇1=0

∴θt+1=θt+α(Gt−b(st))∇log⁡π(At|St;θt)

为估计值b(st)=v^(st,w),v^为估计值

θt+1=θt+α(Gt−v^(st,w))∇log⁡π(At|St;θt)

θt+1=θt+α(rt+γv^(st+1)−v^(st,w))∇log⁡π(At|St;θt)

此时除了训练策略函数

，又多要训练值函数

，引出 Actor-Critic 模型

Actor-Critic 算法结合了学习值函数和策略函数

θt+1=θt+α(rt+γv^(st+1)−v^(st,w))∇log⁡π(At|St;θt)

Actor ->

π(a|s)

，Critic ->

v^(s)

，这一系列算法的目标都是，优化一个带参数的策略，只是会额外学习值函数去帮助策略函数更好的学习，所以本质上还是属于policy-based方法

8.TRPO 但以上policy-based方法都会遇到训练不稳定的情况，所以考虑在更新时找到一块 Trust Region，能够得到策略性能的安全性保证，引出了 TRPO 置信区域策略优化算法在理论上能保证策略学习的性能单调性，实际中取得比策略梯度算法更好的效果

因为该算法比较复杂，使用了泰勒展开近似，共轭梯度，线性搜索等方法直接求解，计算过程十分复杂，运算量非常大，而且也被相对简单的 PPO 因计算量低且性能相当的优势所替代，在此就不做过多赘述

9.PPO

使用了相对简单的方法 PPO 求解，大量实验结果证明效果和 TRPO 一样好近端策略优化（Proximal Policy Optimization）是一种 actor-critic RL 算法，广泛应用于 LLM 强化微调阶段和足式机器人训练

回顾一下之前提到的时序差分，来计算 PPO 所需要的广义优势估计 GAE

一步时序差分更新 V 函数：

V(st)=V(st)+α[rt+γV(st+1)−V(st)]=V(st)+αδt
时序差分：

At(1)=δt=rt+γV(st+1)−V(st)At(2)=δt+γδt+1=rt+γrt+1+γ2V(st+2)−V(st)=[rt+γV(st+1)−V(st)]+γ[rt+1+γV(st+2)−V(st+1)]At(3)=δt+γδt+1+γ2δt+2=rt+γrt+1+γ2rt+2+γ2V(st+3)−V(st)At(k)=∑i=0k−1γiδt+i
GAE 广义优势估计：时序差分不同步数的优势估计进行指数加权平均

AtGAE=(1−λ)(At(1)+λAt(2)+λ2At(3)+...)=(δt+λγδt+1+λ2γ2δt+2+...)

γλAt+1GAE=λγ(δt+1+λγδt+2+...)=(λγδt+1+λ2γ2δt+2+...)

'
GAE 逆向迭代计算

At=δt+γλAt+1

λ∈[0,1]

，是 GAE 额外引入的一个超参数 λ=0

只看一步差分得到的优势；λ=1

看每一步差分得到优势的平均值
Actor 目标函数：

JPPO(θ)=Eπθold[min[πθ(a|s)πθold(a|s)At,clip(πθ(a|s)πθold(a|s),1−ϵ,1+ϵ)At]]

At=∑i=0Tλiγiδt+i

多步时序差分残差的指数加权 δt=rt+γV(st+1)−V(st)

一步时序差分残差 𝑟𝑡=𝑟ϕ(s)−βlogπθ(a|s)π𝑟𝑒𝑓(a|s)**

是奖π𝑟𝑒𝑓

是参考策略 (即 SFT 的初始模型)，β

为 KL 惩罚项系数**

At=∑i=0Tλiγi(𝑟ϕ(s)−βlogπθ(at+i|st+i)π𝑟𝑒𝑓(at+i|st+i)+γV(st+i+1)−V(st+i))

求 PPO 策略梯度

∇JPPO(θ)=πθ(a|s)πθold(a|s)At∇log⁡π(At|St;θt)≈At∇log⁡π(At|St;θt)

策略网络更新

θt+1=θt+αAt∇log⁡π(At|St;θt)

Critic 目标值函数 V(s)： Jcritic=(rt+γV(st+1)−V(st))2

重要性采样的近似和 PPO 中的 clip

重要性采样基于 model-free 的强化学习，通常会使用 MC 采样方法中的离轨策略估计
V(s)
，来评估π′
实际中，大多只能从旧策略 πθold
采样，因此引出重要性采样： J(θ)=∑oR(o)πθ(o)=∑oR(o)πθold(o)πθ(o)πθold(o)=E[o∼πθ]R(o)=E[o∼πθold]R(o)πθ(o)πθold(o)
这样可以从πθold
采样，重要性采样比值 πθ(o)πθold(o)=πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)=ri,t
来修正新旧策略分布偏差 ri,t=πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)
是重要性采样比值尽量不要使得 πθ(o)πθold(o)
差异太大，因为对旧策略 πθold
采样，πθold
概率很小时，样本重要性反而很大，也会降低采样效率，所以引入了 clip 机制和 KL 散度，让两概率分布差异减少
clip 机制新旧策略差距较大时，
ri,t
可能会过大或过小导致训练不稳定，甚至梯度爆炸 PPO 通过引入 clip 机制，限制 ri,t
的变化 L(θ)=min[πθ(ot|q,o<t)πθold(ot|q,o<t),clip(πθ(ot|q,o<t)πθold(ot|q,o<t),1−ϵ,1+ϵ)]
ri,t
偏离 1 太多，就会被裁剪到 [1−ϵ,1+ϵ]
范围内，避免训练不稳定

具体而言，PPO 使用了对 TRPO 优化的一阶近似，对最大化的目标函数做了 CLIP 裁剪的创新技巧换言之，也就是对目标函数的悲观估计，可以每次少量优化，防止优化策略过大和训练不稳定，增加模型的鲁棒性或者用 KL 散度惩罚项来替代 CLIP 裁剪，所以 PPO 分两种形式，PPO-Penality 和 PPO-Clip

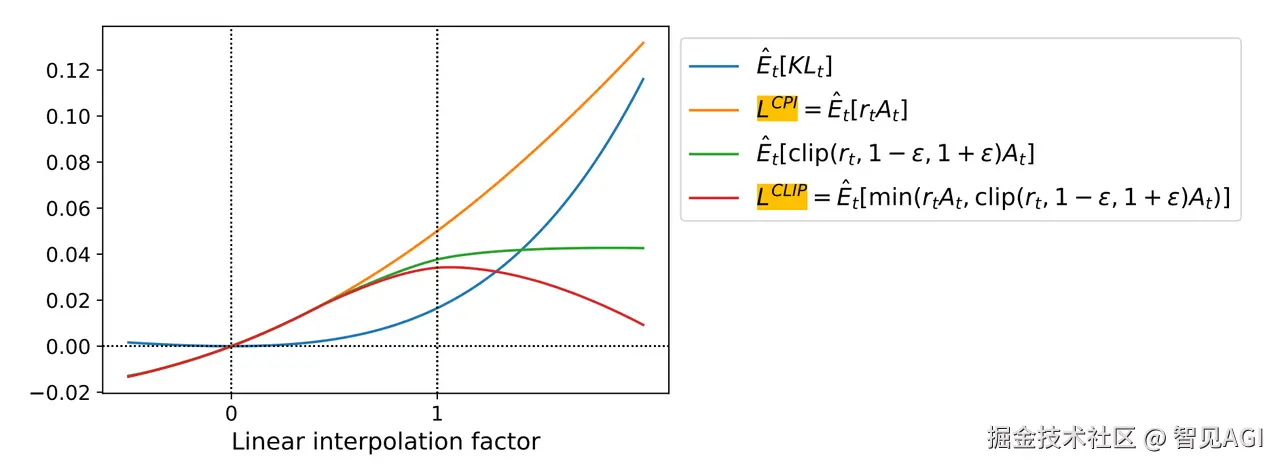
PPO 使用一个深度神经网络来表示策略

π(a|s,θ)

，其中 θ 是策略网络的参数策略网络的输入是当前状态 s，输出是每个动作 a 的概率分布，表示在状态 s 下采取不同动作的可能性与 DQN 类似，策略网络的结构也取决于任务类型，可以是 CNN 或 MLP 但要多训练一个值函数网络

V(s;θ)

，用 CNN 或 MLP

10.GRPO

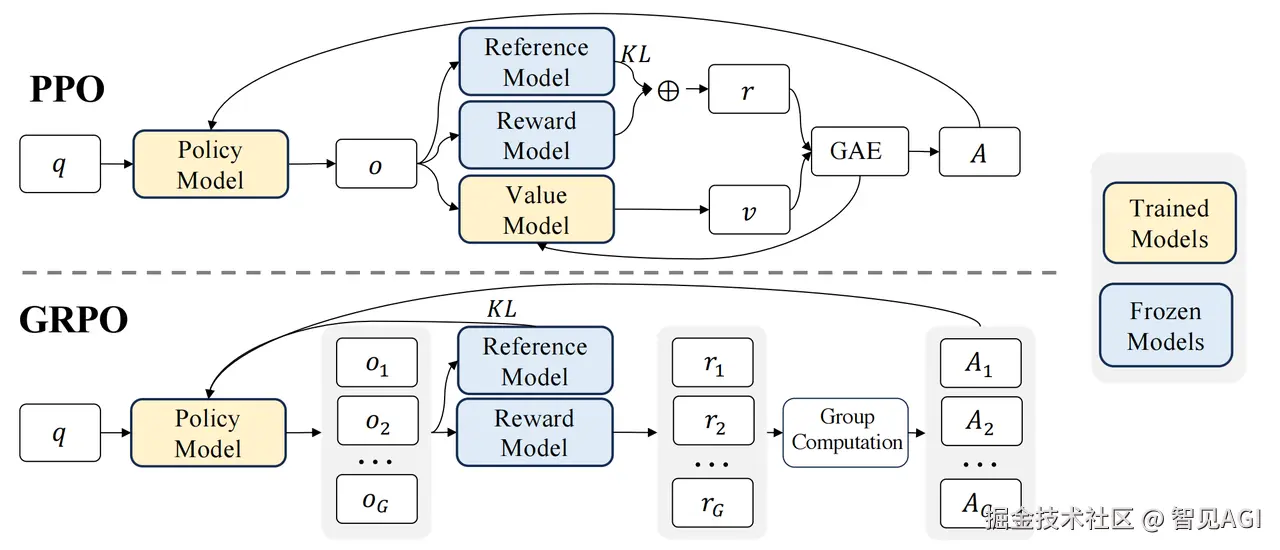
Group Relative Policy Optimization (GRPO) 是 Proximal Policy Optimization (PPO) 近端策略优化的变种放弃了值模型和 critic 模型，从群奖励分数取计算Adventage，更新策略函数，大幅减少计算量

JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O|q)]1G∑i=1G1|oi|∑t=1|oi|{min[πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t,clip[πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t),1−ϵ,1+ϵ]A^i,t]−βDKL[πθ||πref]}

A^𝑖,𝑡=𝑟𝑖−1G∑i=1G𝑟𝑖σr, 1
从上述公式可以看出JGRPO(θ)eta)
，而公式πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t,t}
，其他项为修正项

不考虑 KL 惩罚项和 clip 裁剪项的情况下：根据重要性采样

JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O|q)]1G∑i=1G1|oi|∑t=1|oi|πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t=E[q∼P(Q),{oi}i=1G∼πθ(O|q)]1G∑i=1G1|oi|∑t=1|oi|A^i,t=E[q∼P(Q),{oi}i=1G∼πθ(O|q)]1G∑i=1GA^i=E[q∼P(Q),{oi}i=1G∼πθ(O|q)]1G∑i=1G𝑟𝑖−μrσr=1Gσr∑i=1GEq∼P(Q),{oi}i=1G∼πθ(O|q)

在新策略πθ

已知的情况下，1Gσr

是常数所以要使JGRPO(θ)

在更新策略后增大，需要让∑i=1GEq∼P(Q),{oi}i=1G∼πθ(O|q)

变大显而易见，根据问题回答的G个答案中：回答好的oi**的r_i

t;0

**的r_i

t;0

的条件概率分布，向回答 reward 值高的方向增大概率，JGRPO(θ)

会增大，从而达到优化效果****
而

D𝐾𝐿[πθ||π𝑟𝑒𝑓]

反映的是更新策略与参考策略的概率分布差异大小，有点像策略概率分布的 "正则化" 让每一次策略更新的差异不那么大，一步一个脚印慢慢优化πθ

，有助于训练的稳定性 D𝐾𝐿[πθ||π𝑟𝑒𝑓]=π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−logπ𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−1 1
运用策略梯度优化，不考虑裁剪项:

JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O|q)]1G∑i=1G1|oi|∑t=1|oi|πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t−βDKL[πθ||πref]=E[q∼P(Q),{oi}i=1G∼πθold(O|q)]1G∑i=1G1|oi|∑t=1|oi|πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t−β(π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−logπ𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−1) )

运用

∇πθ=πθ∇logπθ

似然比技巧求梯度

∇θJGRPO(θ)=1G∑i=1G1|oi|∑t=1|oi|[ πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t∇θlogπθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−β(−π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ2(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)+πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ2(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡))πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)∇θlogπθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)] =1G∑i=1G1|oi|∑t=1|oi|[ πθ(oi,t|q,oi,<t)πθold(oi,t|q,oi,<t)A^i,t−β(1−π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡))] ∇θlogπθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)t;𝑡})}

因为有kl散度惩罚项，一次策略改进变化较小，所以令

πθ(oi,t|q,oi,<t)≈πθold(oi,t|q,oi,<t)

∴∇θJGRPO(θ)=1G∑i=1G1|oi|∑t=1|oi|[ A^i,t+β(π𝑟𝑒𝑓(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)πθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)−1)] ∇θlogπθ(𝑜𝑖,𝑡|𝑞,𝑜𝑖,<𝑡)})}

总结

强化学习在LLM领域的应用远未到终点，其前景非常广阔，目前的热门方向大致如下：

自动化与AI反馈 (RLAIF)

人类反馈成本高昂且速度慢。未来，强大的AI模型可以代替人类来提供反馈信号，这个概念被称为RLAIF (Reinforcement Learning from AI Feedback)
一个更强大的"教师"AI可以评估"学生"AI的回答，并提供奖励信号，从而实现大规模、自动化的持续改进和对齐

与工具使用的深度融合

未来的LLM不仅是语言模型，更是能调用各种工具（如代码解释器、搜索引擎、API）的"智能体"（Agent）。
强化学习是训练智能体的核心技术。通过奖励模型来判断工具使用的有效性，RL可以教会LLM何时、如何以及为何使用工具，从而解决更复杂的现实世界问题

总而言之，强化学习已经成为释放大型语言模型全部潜力的核心技术之一。它不仅解决了关键的"对齐"问题，更指明了通往更强大、更通用、更能解决现实问题的AI智能体的道路

参考资料 Proximal Policy Optimization Algorithms, John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, Oleg Klimov, OpenAI DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning, DeepSeek-AI DAPO: An Open-Source LLM Reinforcement Learning System at Scale, ByteDance Seed, Institute for AI Industry Research (AIR), Tsinghua University, The University of Hong Kong , SIA-Lab of Tsinghua AIR MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention, MiniMax Reinforcement Learning Richard S. Sutton 动手学强化学习张伟楠强化学习的数学原理赵世钰强化学习白板推导系列 B站up主: shuhuai008