【多模态大模型面经】现代大模型架构（一）: 组注意力机制（GQA）和 RMSNorm

九年义务漏网鲨鱼2025-11-21 12:37

🧔 这里是九年义务漏网鲨鱼，研究生在读，主要研究方向是人脸伪造检测,长期致力于研究多模态大模型技术；国家奖学金获得者，国家级大创项目一项，发明专利一篇，多篇论文在投，蓝桥杯国家级奖项、妈妈杯一等奖。

✍ 博客主要内容为大模型技术的学习以及相关面经，本人已得到B站、百度、唯品会等多段多模态大模型的实习offer，为了能够紧跟前沿知识，决定写一个"从零学习 RL"主题的专栏。这个专栏将记录我个人的主观学习过程，因此会存在错误，若有出错，欢迎大家在评论区帮助我指出。除此之外，博客内容也会分享一些我在本科期间的一些知识以及项目经验。

🌎 Github仓库地址：Baby Awesome Reinforcement Learning for LLMs and Agentic AI

📩 有兴趣合作的研究者可以联系我：yirongzzz@163.com

文章目录

    • 前言
    • 一、现如今的"Transformer"
    • [二、Attention Serious](#二、Attention Serious)
      • [2.1 Multi-Head Attention (MHA)](#2.1 Multi-Head Attention (MHA))
      • [2.2 Multi-Query Attention (MQA)](#2.2 Multi-Query Attention (MQA))
      • [2.3 Grouped Query Attention (GQA)](#2.3 Grouped Query Attention (GQA))
    • [三、归一化：LayerNorm → RMSNorm + Pre-Norm](#三、归一化：LayerNorm → RMSNorm + Pre-Norm)
        • [🔹 Post-Norm（原始 Transformer 用法）](#🔹 Post-Norm（原始 Transformer 用法）)
        • [🔹 Pre-Norm（现代 LLM 常用）](#🔹 Pre-Norm（现代 LLM 常用）)
      • [3.1 LayerNorm](#3.1 LayerNorm)
        • [🧠 1.为什么不用 BatchNorm，而用 LayerNorm / RMSNorm？(面经)](#🧠 1.为什么不用 BatchNorm，而用 LayerNorm / RMSNorm？(面经))
      • [3.2 RMSNorm](#3.2 RMSNorm)
    • 四、总结

前言

✍ 在大模型论文学习中，相信很多读者和笔者一样，一开始都会有一种感觉："现在大模型架构都差不多，主要是数据和算力在堆积。"当笔者慢慢总结LLaMA、Qwen、DeepSeek这些模型架构的时候发现，在 Attention、位置编码、FFN 与归一化 上，其实已经悄悄从经典 Transformer 走到了另一套"默认配置"。相较于最初的 Transformer，现在的主流大模型在架构上，已经逐渐从：

  • MQA → GQA（Grouped Query Attention）
  • 绝对位置编码 → RoPE（Rotary Positional Embedding）
  • ReLU / GELU 前馈网络 → SwiGLU 前馈网络
  • LayerNorm → RMSNorm + Pre-Norm
  • ...

因此，在本文的学习中，我们主要聚焦于目前的大模型"默认配置"的学习，了解现在的"Transformer"!

一、现如今的"Transformer"

读者肯定很疑惑，为什么我要把第一章名字起为现如今的"Transformer"，实际上在以前，不管是科研还是工作，大家都会把Transformer作为一个baseline去进行优化，就像BERT、GPT等等，一直沿用的是Transformer的架构。但到了现在，研究者发现其中模块的更替可以达到更好的的效果。因此，现如今的大模型，已经不再直接将以前的Transformer架构作为baseline，而是将更换了模块的Transformer架构作为baseline。那现如今的baseline模块长什么样子呢，笔者统计了比较经典的模块所采用的注意力机制、位置编码、MLP激活层以及归一化的方式:

模型家族 注意力 位置编码 MLP 激活 归一化
早期 GPT/BERT MHA 绝对 PE / learned pos GELU LayerNorm
LLaMA 1/2/3 系列 GQA（大模型） RoPE SwiGLU RMSNorm
Qwen2 / Qwen2.5 GQA RoPE SwiGLU RMSNorm
Mistral 7B GQA + sliding window RoPE SwiGLU RMSNorm
DeepSeek-LLM 等 GQA/自研高效注意力 RoPE SwiGLU RMSNorm
Granite / Gemma 等 GQA/MQA RoPE SwiGLU/GeGLU RMSNorm/LN

如表格所示, 对比早期 GPT/BERT 模型我们就可以发现了，现如今大模型的各个模块都有所改变：

  • 注意力机制：MQA → GQA（Grouped Query Attention）
  • 位置编码： 绝对位置编码 → RoPE（Rotary Positional Embedding）
  • MLP 激活层：ReLU / GELU 前馈网络 → SwiGLU 前馈网络
  • 归一化： LayerNorm → RMSNorm + Pre-Norm

所以如果你能把这四件套讲明白，基本就把现代 LLM 架构里 理清，并且可以快速找到文章的贡献点。

二、Attention Serious

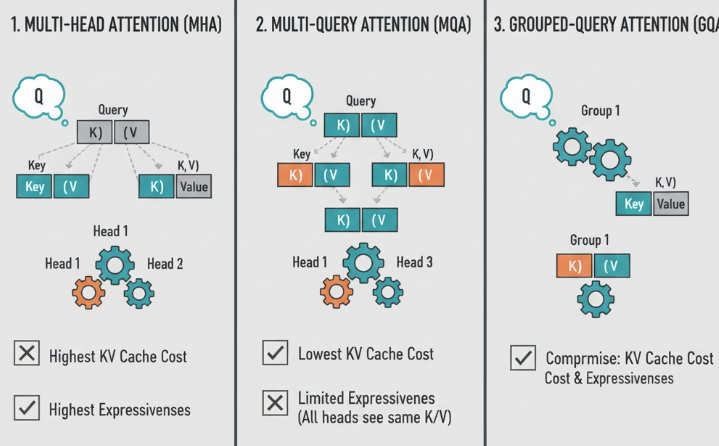
2.1 Multi-Head Attention (MHA)

首先来回顾一下以前的注意力机制：
Attention ( Q , K , V ) = softmax ( Q K ⊤ d k ) V \text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dk QK⊤)V

在标准的自注意力中，我们通过 Q K T / d k QK^T / \sqrt{d_k} QKT/dk 来计算不同 token 之间的注意力权重。但作者发现，仅用一个注意力头往往难以同时捕捉多种语义关系（如词法、语义、句法等）。因此，Transformer 提出了多头注意力机制 (Multi-Head Attention, MHA)。

将输入特征通过不同的线性投影矩阵，映射到多个低维子空间中：
head i = Attention ( Q W i Q ,   K W i K ,   V W i V ) \text{head}_i = \text{Attention}(QW_i^Q, \, KW_i^K, \, VW_i^V) headi=Attention(QWiQ,KWiK,VWiV)

然后将所有头拼接（concatenate）再线性变换：
MultiHead ( Q , K , V ) = Concat ( head 1 , ... , head h ) W O \text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O MultiHead(Q,K,V)=Concat(head1,...,headh)WO

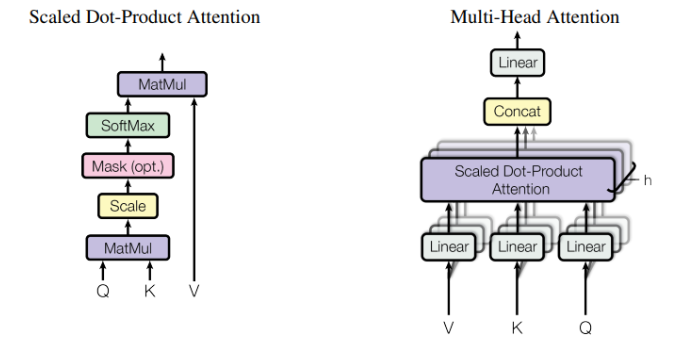
MHA通过多个小头可以从不同角度捕捉语义信息，增强模型的表达能力和稳定性，比单头更鲁棒。

  • 代码手撕
python 复制代码 
import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, dropout=0.0):
        super().__init__()
        assert d_model % num_heads == 0
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads

        self.w_q = nn.Linear(d_model, d_model)
        self.w_k = nn.Linear(d_model, d_model)
        self.w_v = nn.Linear(d_model, d_model)
        self.w_o = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, attn_mask=None):
        """
        x: [B, L, d_model]
        """
        B, L, _ = x.size()

        # 1. 线性投影
        Q = self.w_q(x)  # [B, L, d_model]
        K = self.w_k(x)
        V = self.w_v(x)

        # 2. reshape 为 [B, H, L, Dh]
        def reshape_heads(t):
            return t.view(B, L, self.num_heads, self.head_dim).transpose(1, 2)
        Q = reshape_heads(Q)
        K = reshape_heads(K)
        V = reshape_heads(V)
        # Q,K,V: [B, H, L, Dh]

        # 3. 缩放点积注意力
        scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5)  # [B, H, L, L]
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask == 0, float('-inf'))
        attn = F.softmax(scores, dim=-1)
        attn = self.dropout(attn)

        out = attn @ V  # [B, H, L, Dh]

        # 4. 合并头
        out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
        return self.w_o(out)

2.2 Multi-Query Attention (MQA)

有了 MHA 之后，大家第一反应是：头越多越好，越能学到多种语义关系。但在大模型、尤其是 Decoder-Only + 长上下文 + 自回归生成 的场景下，MHA 暴露出了一个非常现实的问题：

KV Cache 太贵了。

在自回归生成过程中，每生成一个新 token，都需要用到历史所有位置的 K , V K, V K,V

  • 对于标准 MHA：每个注意力头都维护一份自己的 K h , V h K_h, V_h Kh,Vh
  • 如果有 h h h 个头，那么 KV Cache 的内存开销大致是: O ( h ⋅ L ⋅ d head ) \mathcal{O}(h \cdot L \cdot d_{\text{head}}) O(h⋅L⋅dhead)

当我们把头数堆到 32、64 甚至更多，再把上下文长度拉到 32K、64K 时，这个开销就会变成显存吞噬怪，直接限制推理速度与可部署性。因此，为了在几乎不损失模型效果的前提下，压缩 KV Cache 和带宽成本，就提出了 Multi-Query Attention（MQA）。

MHA中的每一个头都是独享一份 K , V K, V K,V，相反的，MQA 提出了所有的头共享同一份 K , V K, V K,V也就是说，只保留一组 WK,WVW^K, W^VWK,WV，而 WiQW_i^QWiQ 仍然为每个头独立：
Q i = X W i Q , K = X W K , V = X W V . Q_i = X W_i^Q,\quad K = X W^K,\quad V = X W^V. Qi=XWiQ,K=XWK,V=XWV.

于是每个头的注意力就变成：
head i = Attention ( Q i , K , V ) = softmax ( Q i K ⊤ d k ) V . \text{head}_i = \text{Attention}(Q_i, K, V) = \text{softmax}\left(\frac{Q_i K^\top}{\sqrt{d_k}}\right) V. headi=Attention(Qi,K,V)=softmax(dk QiK⊤)V.

最后依然是拼接再线性变换：
MQA ( X ) = Concat ( head 1 , ... , head h ) W O . \text{MQA}(X) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O. MQA(X)=Concat(head1,...,headh)WO.

💡 经验发现"多 KV"并没有带来线性收益, Q 仍然是多头的，多头仍能捕捉多种语义关系。

  • 代码手撕
PYTHON 复制代码 
class MultiQueryAttention(nn.Module):
    def __init__(self, d_model, num_heads, dropout=0.0):
        super().__init__()
        assert d_model % num_heads == 0
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads

        self.w_q = nn.Linear(d_model, d_model)
        # 注意：K/V 只有一组，所以输出维度是 head_dim
        self.w_k = nn.Linear(d_model, self.head_dim)
        self.w_v = nn.Linear(d_model, self.head_dim)
        self.w_o = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, attn_mask=None):
        """
        x: [B, L, d_model]
        """
        B, L, _ = x.size()

        # 1. 多头 Q
        Q = self.w_q(x)  # [B, L, d_model]
        Q = Q.view(B, L, self.num_heads, self.head_dim).transpose(1, 2)
        # Q: [B, H, L, Dh]

        # 2. 单头 K/V
        K = self.w_k(x)  # [B, L, Dh]
        V = self.w_v(x)  # [B, L, Dh]

        # 3. 为了和 Q 匹配，将 K/V 在头维上 broadcast
        K = K.unsqueeze(1)  # [B, 1, L, Dh]
        V = V.unsqueeze(1)  # [B, 1, L, Dh]
        K = K.expand(B, self.num_heads, L, self.head_dim)
        V = V.expand(B, self.num_heads, L, self.head_dim)

        # 4. 缩放点积注意力（与 MHA 相同）
        scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5)  # [B, H, L, L]
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask == 0, float('-inf'))
        attn = F.softmax(scores, dim=-1)
        attn = self.dropout(attn)

        out = attn @ V  # [B, H, L, Dh]
        out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
        return self.w_o(out)

2.3 Grouped Query Attention (GQA)

根据前面两节的分析，我们可以总结出：

  • MHA ：每个头都有独立的 K h , V h K_h, V_h Kh,Vh，表达能力强，但 KV Cache 成本最高；
  • MQA ：所有头共享同一份 K , V K, V K,V，KV Cache 成本最低，但多头之间视角差异弱，表达能力稍打折

于是就自然出现了一个折中思路：能不能在 "省 KV" 和 "头之间有点差异" 之间找个平衡？这就是 Grouped-Query Attention（GQA）。GQA 的核心思想：Q 仍然是很多头，但 K/V 的头数减少为更少的组（num_kv_heads），每组 KV 服务若干个 Q 头。

  • 代码手撕
python 复制代码 
class GroupedQueryAttention(nn.Module):
    def __init__(self, d_model, num_q_heads, num_kv_heads, dropout=0.0):
        super().__init__()
        assert d_model % num_q_heads == 0
        assert num_q_heads % num_kv_heads == 0

        self.d_model = d_model
        self.num_q_heads = num_q_heads
        self.num_kv_heads = num_kv_heads
        self.head_dim = d_model // num_q_heads
        self.group_size = num_q_heads // num_kv_heads  # 每组多少个 Q 头共享一个 KV

        self.w_q = nn.Linear(d_model, d_model)
        self.w_k = nn.Linear(d_model, num_kv_heads * self.head_dim)
        self.w_v = nn.Linear(d_model, num_kv_heads * self.head_dim)
        self.w_o = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, attn_mask=None):
        """
        x: [B, L, d_model]
        """
        B, L, _ = x.size()

        # 1. Q: 多头； K/V: 少量头
        Q = self.w_q(x)  # [B, L, d_model]
        K = self.w_k(x)  # [B, L, num_kv_heads * head_dim]
        V = self.w_v(x)

        Q = Q.view(B, L, self.num_q_heads, self.head_dim).transpose(1, 2)
        K = K.view(B, L, self.num_kv_heads, self.head_dim).transpose(1, 2)
        V = V.view(B, L, self.num_kv_heads, self.head_dim).transpose(1, 2)
        # Q: [B, Hq,  L, Dh]
        # K,V: [B, Hkv, L, Dh]

        # 2. 将每个 KV 头"扩展"为 group_size 个 Q 头使用
        #    例如 Hq=8, Hkv=2 -> group_size=4
        K = K.repeat_interleave(self.group_size, dim=1)  # [B, Hq, L, Dh]
        V = V.repeat_interleave(self.group_size, dim=1)

        # 3. 缩放点积注意力
        scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5)  # [B, Hq, L, L]
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask == 0, float("-inf"))
        attn = F.softmax(scores, dim=-1)
        attn = self.dropout(attn)

        out = attn @ V  # [B, Hq, L, Dh]

        # 4. 合并头
        out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
        return self.w_o(out)

三、归一化：LayerNorm → RMSNorm + Pre-Norm

在 Transformer 里，归一化（Normalization）主要解决两个问题：

  1. 深层网络训练不稳定：梯度可能爆炸或消失；
  2. 不同层输出分布漂移，导致学习变慢。

最早的 Transformer 使用的是 LayerNorm + Post-Norm 残差结构 （指在全连接层后跟上一个归一化层）

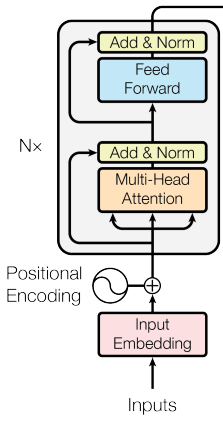
但到了 LLaMA、DeepSeek 等大模型时，大家开始逐渐转向：RMSNorm + Pre-Norm （指在全连接层前跟上一个归一化层）

🔹 Post-Norm（原始 Transformer 用法）

最早的 Transformer 论文（Attention Is All You Need）使用的是 Post-Norm,代码结构类似：

python 复制代码 
# Post-Norm 结构
out = x + sublayer(x)
out = layer_norm(out)
🔹 Pre-Norm（现代 LLM 常用）

大多数现代 LLM（如 LLaMA、DeepSeek 系列）改成了 Pre-Norm：代码结构类似：

python 复制代码 
# Pre-Norm 结构
h = layer_norm(x)
out = x + sublayer(h)

💡 实践上，Pre-Norm 再配合 RMSNorm，只调节尺度不改均值，在 Decoder-only 结构里训练更稳定、实现也更简单。

3.1 LayerNorm

Layer Normalization（LN）是在 Transformer 中使用最广的归一化方式之一。给定一个 token 的隐藏表示 x ∈ R d x \in \mathbb{R}^{d} x∈Rd，LayerNorm 对其 特征维度 进行归一化：
μ = 1 d ∑ i = 1 d x i , σ 2 = 1 d ∑ i = 1 d ( x i − μ ) 2 \mu = \frac{1}{d} \sum_{i=1}^{d} x_i,\quad \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 μ=d1i=1∑dxi,σ2=d1i=1∑d(xi−μ)2

LN ( x ) = x − μ σ 2 + ϵ ⋅ γ + β \text{LN}(x) = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot \gamma + \beta LN(x)=σ2+ϵ x−μ⋅γ+β

其中：

  • γ , β ∈ R d \gamma, \beta \in \mathbb{R}^{d} γ,β∈Rd是可学习的缩放和平移参数；
  • 归一化是在单个样本、单个 token 的通道维度上完成的。

🧠 直觉理解：

对每个 token 的特征做一遍"标准化 + 线性变换"，

让每一层看到的分布更平滑，避免某些维度过大/过小导致训练不稳。

在 PyTorch 中，你平时看到的 nn.LayerNorm 就是这个东西：

python 复制代码 
import torch
import torch.nn as nn

x = torch.randn(2, 4, 8)  # [B, L, d_model]
ln = nn.LayerNorm(8)
y = ln(x)  # 每个位置的最后一维做 LN
🧠 1.为什么不用 BatchNorm，而用 LayerNorm / RMSNorm？(面经)

这一问是面试官很喜欢的一个考点，尤其是 Transformer / LLM 岗位。核心区别在于：归一化时用哪些维度来统计均值与方差。

  • BatchNorm（BN） ：
    • 在 CV 里常用，对 batch 维度 + 空间维度 做统计；
    • 对每个通道c，使用整批数据的统计量： m u c = E N , H , W [ x n , c , h , w ] mu_c = \mathbb{E}{N,H,W}[x{n,c,h,w}] muc=EN,H,W[xn,c,h,w]
  • LayerNorm（LN） ：
    • 对单个样本、单个 token 的所有特征求均值和方差，不依赖 batch 大小。

在 Transformer / LLM 场景中，BN 存在几个问题：

  1. 序列长度不固定：BN 在变长序列上不自然，统计维度不好选；
  2. 推理阶段 batch 很小甚至为 1：BN 的 running mean/var 与训练时差异大，容易分布漂移；
  3. 自注意力中不同 token 之间差异大：BN 混合不同 token 的统计量，会引入额外噪声。

因此，大模型里更偏向用 LayerNorm / RMSNorm 这种"不依赖 batch、只看自己"的归一化方式。

3.2 RMSNorm

RMSNorm 是基于"层归一化中主要起作用的是缩放因子，而非平移因子"这个发现而提出的归一化方法。在层归一化中需要减去均值，而模型在训练过程中已经学会通过投影矩阵自动调节均值；而 γ \gamma γ 的作用是调整每一维的相对 scale，是表达力的核心。给定 x ∈ R d x \in \mathbb{R}^d x∈Rd，RMSNorm 的公式为：
RMS ( x ) = 1 d ∑ i = 1 d x i 2 + ϵ \text{RMS}(x) = \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2 + \epsilon} RMS(x)=d1i=1∑dxi2+ϵ

RMSNorm ( x ) = x RMS ( x ) ⋅ γ \text{RMSNorm}(x) = \frac{x}{\text{RMS}(x)} \cdot \gamma RMSNorm(x)=RMS(x)x⋅γ

🧠 直觉理解：

RMSNorm 更像是"把这个向量整体缩放到一个合适能量水平"，

不去把它"拉回 0 均值"，只控制它的尺度。

💡 实践上，在 Decoder-only 大模型里：RMSNorm + Pre-Norm 组合在超深层网络（几十层）上表现更稳定，这也是 LLaMA / DeepSeek / Qwen 等系列广泛采用它的原因之一。

  • 代码手撕
python 复制代码 
class RMSNorm(nn.Module):
    def __init__(self, d_model, eps=1e-8):
        super().__init__()
        self.weight = nn.Parameter(torch.ones(d_model))
        self.eps = eps

    def forward(self, x):
        """
        x: [B, L, d_model]
        """
        # 均方根：sqrt(mean(x^2))
        rms = x.pow(2).mean(dim=-1, keepdim=True).add(self.eps).sqrt()
        x_norm = x / rms
        return self.weight * x_norm

四、总结

本章我们先把现代大模型里的两块"基础设施"打牢：一块是从 MHA → MQA → GQA 的注意力演化，用更少的 KV 头（甚至共享 KV）在不明显掉点的前提下，大幅降低 KV Cache 与长上下文显存开销 ；另一块是从 LayerNorm → RMSNorm + Pre-Norm 的归一化升级，用"只归一化能量"的 RMSNorm 配合 Pre-Norm 结构，让超深的 Decoder-only 模型在训练和推理中都更加稳定。后面的章节，我们再把 RoPE / SwiGLU / MoE / MLA 这些"进阶武器"一个个拆开，拼成一整套现代 LLM 的"架构面经图谱"。

相关推荐
n***29321 小时前
机器学习超参数调优
人工智能·机器学习
3***49961 小时前
机器学习培训
人工智能·机器学习
小妖同学学AI1 小时前
开源机器学习课程mlcourse.ai：理论与实践完美结合的AI学习指南
人工智能·机器学习·github项目分享
O***p6041 小时前
机器学习挑战同时也带来了一系列亟待解决的问题。
人工智能·深度学习·机器学习
智算菩萨1 小时前
多峰差分进化算法的理论进展：从生态位到机器学习融合
人工智能
闲人编程1 小时前
CPython与PyPy性能对比：不同解释器的优劣分析
python·算法·编译器·jit·cpython·codecapsule
IT_陈寒1 小时前
Vue3性能优化实战：5个被低估的Composition API技巧让你的应用快30%
前端·人工智能·后端
杜子不疼.1 小时前
【C++】深入解析AVL树：平衡搜索树的核心概念与实现
android·c++·算法
小武~1 小时前
Leetcode 每日一题C 语言版 -- 88 merge sorted array
c语言·算法·leetcode
热门推荐
01GitHub 镜像站点02今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了03UV安装并设置国内源04Google Antigravity：无法登录？早期错误、登录修复和用户反馈指南05【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连06BongoCat - 跨平台键盘猫动画工具07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08Linux下V2Ray安装配置指南09全球最强模型Grok4，国内已可免费使用！（附教程）10Labelme从安装到标注：零基础完整指南