note
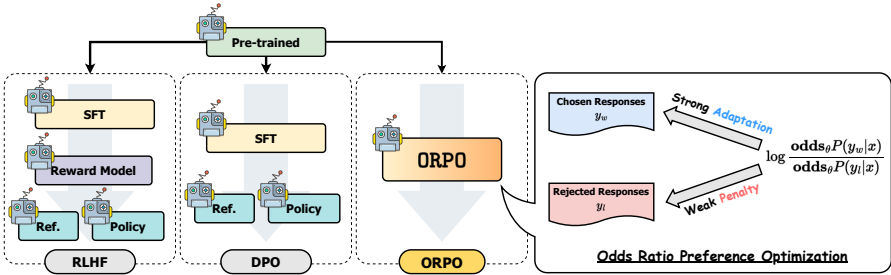
- 本文提出了一种无需参考模型的单片赔率比率偏好优化算法(ORPO),通过重新审视和理解监督微调(SFT)在偏好对齐中的作用,实现了高效的偏好对齐。ORPO在不同规模的预训练语言模型上均表现出色,超越了现有的较大指令跟随语言模型。实验结果表明,ORPO在指令跟随、奖励模型胜率和词汇多样性方面均取得了显著的提升。
- ORPO 的目标函数巧妙地结合了传统的监督微调损失和一个新提出的相对比率损失。
L ORPO = E ( x , y w , y l ) [ L SFT + λ ⋅ L OR ] \mathcal{L}{\text{ORPO}} = \mathbb{E}{(x, y_w, y_l)} \left[ \mathcal{L}{\text{SFT}} + \lambda \cdot \mathcal{L}{\text{OR}} \right] LORPO=E(x,yw,yl)[LSFT+λ⋅LOR]
- L SFT \mathcal{L}_{\text{SFT}} LSFT:监督微调损失,即标准的因果语言建模负对数似然损失,确保模型不遗忘基本的语言生成能力。
- L OR \mathcal{L}_{\text{OR}} LOR:相对比率损失,其目标是拉大模型对"优选响应" ( y_w ) 和"劣选响应" ( y_l ) 的赔率比率,从而让模型学会区分响应优劣。
- ( λ \lambda λ):超参数,用于控制偏好对齐损失的权重。
文章目录
- note
- 一、研究背景
- 二、研究方法
-
- [1. 赔率比率定义](#1. 赔率比率定义)
- [2. 目标函数](#2. 目标函数)
- [3. 梯度计算](#3. 梯度计算)
- 三、实验设计
-
- [1. 数据集](#1. 数据集)
- [2. 模型训练](#2. 模型训练)
- [3. 奖励模型](#3. 奖励模型)
- 四、结果分析
- 五、论文评价
- 六、相关问题
- Reference
一、研究背景
ORPO: Monolithic Preference Optimization without Reference Model
- 研究问题:这篇文章研究了在语言模型的偏好对齐过程中,监督微调(SFT)的关键作用,并提出了一种无需参考模型的单片赔率比率偏好优化算法(ORPO),以消除对额外偏好对齐阶段的依赖。
- 研究难点:现有的偏好对齐方法通常包括多阶段过程,需要额外的参考模型和单独的监督微调预热阶段,这增加了计算复杂度和资源消耗。
- 相关工作:偏好对齐方法包括基于强化学习的对齐方法(如RLHF)、无奖励技术(如DPO)和结合监督微调的对齐方法。这些方法在不同任务上展示了成功,但在效率和性能方面仍有改进空间。
二、研究方法
这篇论文提出了 ORPO 算法,用于解决大语言模型的偏好对齐问题。该方法的核心创新在于将监督微调 和偏好对齐 整合到一个简单的目标函数中,无需采样多个响应或复杂的强化学习流程。
1. 赔率比率定义
首先,算法定义了生成输出序列的概率对数和赔率比率,以量化模型对某个响应的偏好程度。
-
序列生成概率的对数 :
log P θ ( y ∣ x ) = 1 m ∑ t = 1 m log P θ ( y t ∣ x , y < t ) \log P_{\theta}(y\mid x)=\frac{1}{m}\sum_{t=1}^{m}\log P_{\theta}(y_{t}\mid x,y_{<t}) logPθ(y∣x)=m1t=1∑mlogPθ(yt∣x,y<t) -
赔率比率 :
odds θ ( y ∣ x ) = P θ ( y ∣ x ) 1 − P θ ( y ∣ x ) \text{odds}{\theta}(y\mid x)=\frac{P{\theta}(y\mid x)}{1-P_{\theta}(y\mid x)} oddsθ(y∣x)=1−Pθ(y∣x)Pθ(y∣x)
直观解释 :赔率比率 ( odds θ ( y ∣ x ) = k \text{odds}_{\theta} (y\mid x) = k oddsθ(y∣x)=k) 表示模型认为生成输出序列 ( y ) 的概率是不生成它的 ( k ) 倍。该值越大,说明模型越偏好该响应。
2. 目标函数
ORPO 的目标函数巧妙地结合了传统的监督微调损失和一个新提出的相对比率损失。
L ORPO = E ( x , y w , y l ) [ L SFT + λ ⋅ L OR ] \mathcal{L}{\text{ORPO}} = \mathbb{E}{(x, y_w, y_l)} \left[ \mathcal{L}{\text{SFT}} + \lambda \cdot \mathcal{L}{\text{OR}} \right] LORPO=E(x,yw,yl)[LSFT+λ⋅LOR]
- L SFT \mathcal{L}_{\text{SFT}} LSFT:监督微调损失,即标准的因果语言建模负对数似然损失,确保模型不遗忘基本的语言生成能力。
- L OR \mathcal{L}_{\text{OR}} LOR:相对比率损失,其目标是拉大模型对"优选响应" ( y_w ) 和"劣选响应" ( y_l ) 的赔率比率,从而让模型学会区分响应优劣。
- ( λ \lambda λ):超参数,用于控制偏好对齐损失的权重。
3. 梯度计算
相对比率损失 ( L OR \mathcal{L}_{\text{OR}} LOR ) 的梯度计算是其高效性的关键,可分解为两部分:
∇ θ L OR = δ ( d ) ⋅ h ( d ) \nabla_{\theta}\mathcal{L}_{\text{OR}} = \delta(d) \cdot h(d) ∇θLOR=δ(d)⋅h(d)
-
惩罚项 ( δ ( d ) \delta(d) δ(d) ) :
δ ( d ) = [ 1 + odds θ ( y l ∣ x ) odds θ ( y w ∣ x ) ] − 1 \delta(d) = \left[ 1 + \frac{ \text{odds}{\theta} (y_l \mid x) }{ \text{odds}{\theta} (y_w \mid x) } \right]^{-1} δ(d)=[1+oddsθ(yw∣x)oddsθ(yl∣x)]−1该项动态调整更新幅度。当模型已经能够很好地区分优劣响应(即 ( odds θ ( y w ∣ x ) ≫ odds θ ( y l ∣ x ) \text{odds}{\theta} (y_w \mid x) \gg \text{odds}{\theta} (y_l \mid x) oddsθ(yw∣x)≫oddsθ(yl∣x) ))时,( δ ( d ) \delta(d) δ(d) ) 会变小,从而减缓参数更新,起到稳定训练的作用。
-
加权对比项 ( h(d) ) :
h ( d ) = ∇ θ log P θ ( y l ∣ x ) 1 − P θ ( y l ∣ x ) − ∇ θ log P θ ( y w ∣ x ) 1 − P θ ( y w ∣ x ) h(d) = \frac{ \nabla_{\theta} \log P_{\theta}(y_l \mid x) }{ 1 - P_{\theta}(y_l \mid x) } - \frac{ \nabla_{\theta} \log P_{\theta}(y_w \mid x) }{ 1 - P_{\theta}(y_w \mid x) } h(d)=1−Pθ(yl∣x)∇θlogPθ(yl∣x)−1−Pθ(yw∣x)∇θlogPθ(yw∣x)该项构成了对比学习的核心。它通过梯度计算,抑制 模型生成劣选响应 ( y_l ) 的概率,同时促进 模型生成优选响应 ( y_w ) 的概率。
核心优势
ORPO 通过单一阶段、简洁的目标函数,同时实现了模型能力的保持(SFT)和偏好对齐(OR),避免了多阶段训练的复杂性,成为了一种高效且有效的对齐方法。
三、实验设计
1. 数据集
实验使用了两个主流的人类偏好数据集:
- Anthropic的HH-RLHF
- Binarized UltraFeedback
数据过滤:对数据集进行了预处理,排除了以下无效或低质量实例:
- 优选响应和劣选响应相同的情况( y w = y l y_{w} = y_{l} yw=yl)
- 优选响应为空的情况( y w = ∅ y_{w} = \emptyset yw=∅)
- 劣选响应为空的情况( y l = ∅ y_{l} = \emptyset yl=∅)
2. 模型训练
- 模型系列 :实验训练了参数规模从 125M 到 1.3B 不等的 OPT 系列模型。
- 对比方法 :比较了以下几种主要的微调和对齐方法:
- 监督微调(SFT)
- 近端策略优化(PPO)
- 直接策略优化(DPO)
- ORPO训练 :ORPO 模型是在经过SFT 得到的模型基础上进行训练的。
3. 奖励模型
- 模型与规模 :分别使用 OPT-350M 和 OPT-1.3B 模型进行奖励建模。
- 训练方式 :在每个数据集上各训练 1个epoch。
- 用途分配 :
- OPT-350M奖励模型 :用于 PPO 训练过程。
- OPT-1.3B奖励模型 :用于评估 经过微调后模型的生成效果。
四、结果分析
单轮指令跟随:ORPO显著提高了预训练的Phi-2和Llama-2的指令跟随能力。例如,Phi-2+ORPO在AlpacaEval2.0中达到了6.35%的准确率,而Llama-2+ORPO在两个AlpacaEval中分别达到了9.44%和12.20%的准确率。
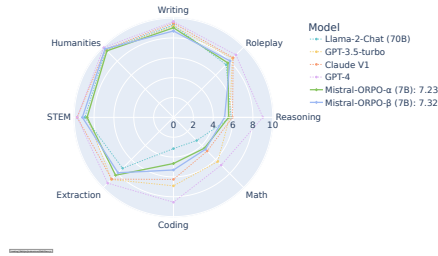
多轮指令跟随:使用最佳模型Mistral-ORPO-α和Mistral-ORPO-β进行评估,结果显示ORPO系列在多轮指令跟随任务中与更大或专有模型的表现相当。
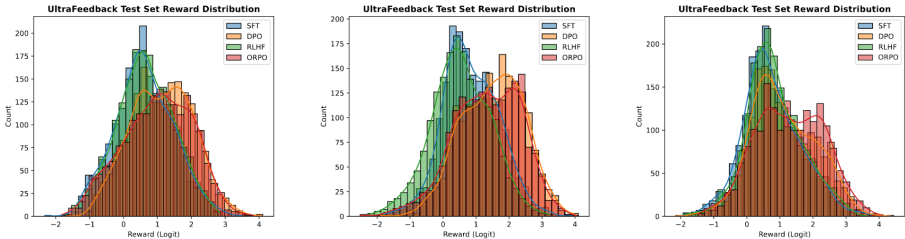
奖励模型胜率:ORPO在所有模型规模上均优于SFT和PPO,最高胜率为79.4%。随着模型规模的增加,ORPO相对于DPO的胜率也逐渐提高。
五、论文评价
1、优点与创新
创新的无参考模型单块偏好优化算法:论文提出了一种名为ORPO(Odds Ratio Preference Optimization)的新算法,该算法无需额外的偏好对齐阶段,直接在监督微调(SFT)过程中动态惩罚不受欢迎的生成风格。
理论分析与实验验证:通过理论分析和实验验证,证明了在SFT过程中使用赔率比(odds ratio)来区分受欢迎和不受欢迎的生成风格是合理的。
跨模型规模的有效性:ORPO在不同规模的模型上均表现出色,从125M到7B的模型在多个基准测试中均超越了现有的最先进语言模型。
资源高效的开发:由于不需要参考模型和SFT预热阶段,ORPO在资源利用上更加高效,有助于偏好对齐模型的快速发展。
多任务评估:在AlpacaEval、IFEval和MT-Bench等多个流行的任务和数据集上进行了广泛的评估,展示了ORPO的有效性和可扩展性。
2、不足与反思
方法比较范围有限:尽管论文对多种偏好对齐方法(包括DPO和RLHF)进行了全面分析,但未能涵盖更广泛的偏好对齐算法进行比较。
数据集和质量的多样性:未来工作将扩展微调数据集到更多样化的领域和质量,以验证方法在各种自然语言处理下游任务中的泛化能力。
内部影响研究:将进一步研究ORPO对预训练语言模型的内部影响,不仅限于监督微调阶段,还包括连续的偏好对齐算法。
六、相关问题
问题1:ORPO算法在实验中是如何验证其有效性的?
单轮指令跟随:ORPO显著提高了预训练的Phi-2和Llama-2的指令跟随能力。例如,Phi-2+ORPO在AlpacaEval2.0中达到了6.35%的准确率,而Llama-2+ORPO在两个AlpacaEval中分别达到了9.44%和12.20%的准确率。
多轮指令跟随:使用最佳模型Mistral-ORPO-α和Mistral-ORPO-β进行评估,结果显示ORPO系列在多轮指令跟随任务中与更大或专有模型的表现相当。
奖励模型胜率:ORPO在所有模型规模上均优于SFT和PPO,最高胜率为79.4%。随着模型规模的增加,ORPO相对于DPO的胜率也逐渐提高。
词汇多样性:ORPO模型在输入内多样性和跨输入多样性方面表现优异。与DPO相比,ORPO模型在生成更具指令特异性的响应方面表现更好。
问题2:ORPO算法与现有的偏好对齐方法相比有哪些优势?
无需参考模型:ORPO算法不需要额外的参考模型,简化了计算复杂度和资源消耗。
高效性:由于不需要参考模型,ORPO在内存分配和每批次的FLOPs方面都更加高效。
理论支持:通过理论分析和实验验证,ORPO在偏好对齐过程中能够有效地平衡对选择响应和拒绝响应的惩罚,避免过度抑制不受欢迎的生成风格。
广泛适用性:ORPO在不同规模的预训练语言模型上均表现出色,超越了现有的较大指令跟随语言模型,验证了其广泛的适用性和有效性。
Reference
1\] ORPO: Monolithic Preference Optimization without Reference Model