文章目录
- 前言
- 一、数据结构基础
- 二、顺序表(SEQUENTIAL_LIST)
- 三、单向链表(LINK_LIST)
- 四、双向链表(DLINK_LIST)
-
- 循环链表(双向循环链表为例)
- 五、栈
-
- 顺序栈(SEQUENTIAL_STACK)
- 链式栈(LINK_STACK)
- 六、队列(queue)
-
- 顺序循环队列
- 链式队列
- 七、二叉树(Binary Tree)与BST(Binary Search Tree)二叉搜索树
- 八、通用型容器
- 总结
前言
一、数据结构基础
1.逻辑关系,存储形式
逻辑关系分为线性关系,非线性关系。
线性关系,例如线性表,栈,队等。非线性关系,图,树等。
2.时间复杂度、空间复杂度
时间复杂度,一个程序中语句的最高执行频次。
空间复杂度 ,一个程序所开辟的内存消耗。
学习数据结构最主要的就是学习其增删查改。
二、顺序表(SEQUENTIAL_LIST)
数组就是一个的典型的顺序表,但是由于数组存在于栈区大小有限,并且较简单。
因此我们着重学习的是堆区的顺序表,即malloc()开辟堆内存。
顺序表由两部分堆区域构成,一部分是顺序表的管理结构体堆区域,一部分是存储数据的堆区域。
顺序表管理结构体
c
int capacity; //管理结构体的容量大小
int index; //存储的是数据下标
int *data_p; //指向数据区域的指针,由该指针指向的堆区域存储数据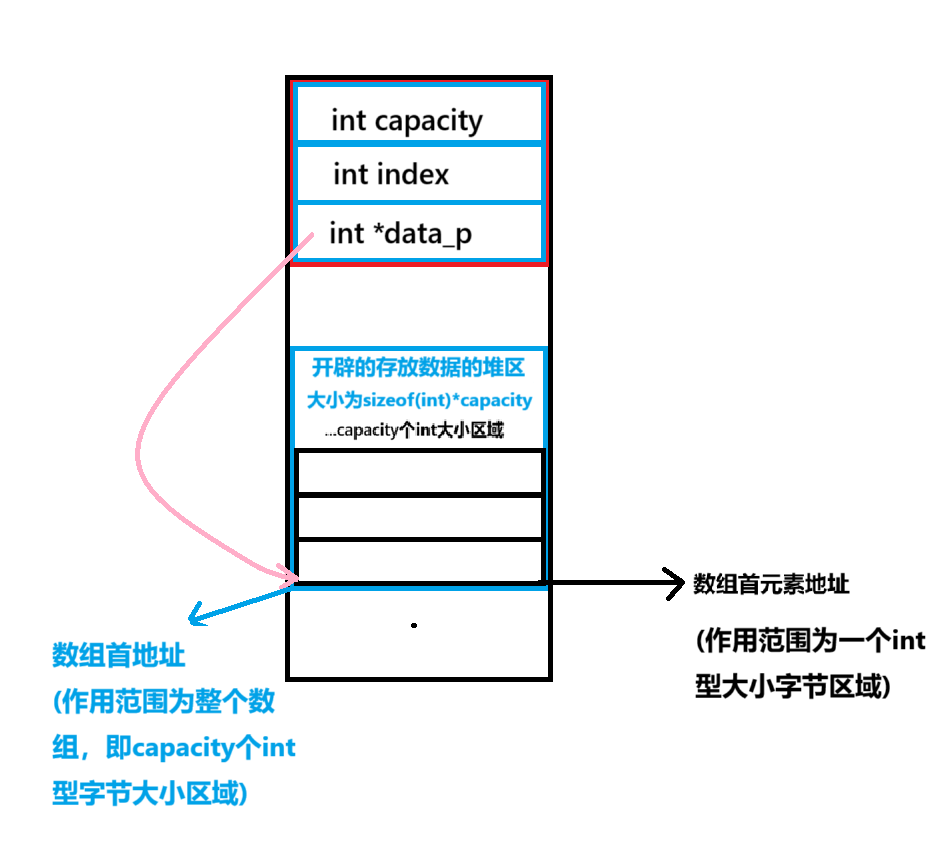
顺序表对应在数组中的表示:
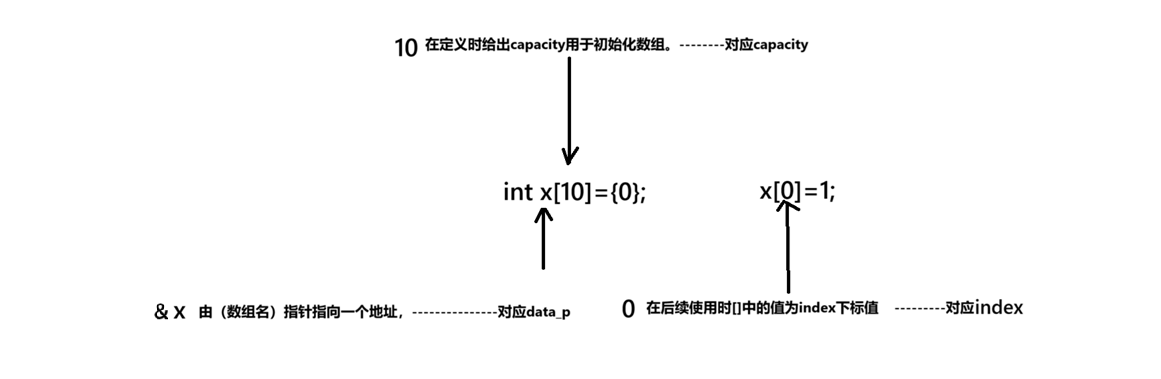
其中需要注意的是&x对应的data_p指针,该指针的作用域范围为(整个数组的大小)即int型大小的元素.所以我们在说数组的数组名代表什么时常常说的是数组首元素的地址 而非 数组首地址虽然他们地址相同 但是作用范围不同。
1.初始化顺序表
初始化顺序表的步骤:
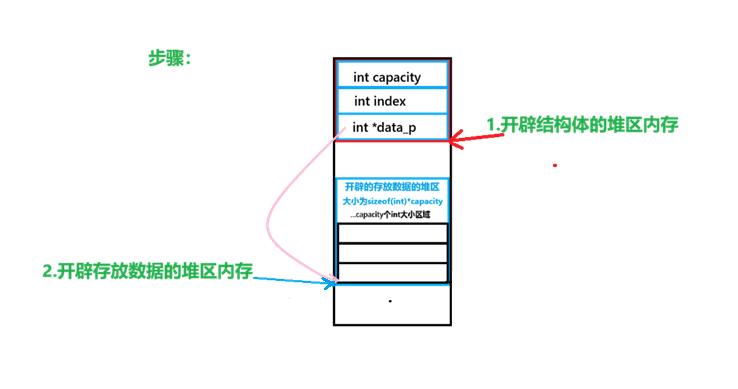
c
typedef struct seqlist //管理结构体
{
int capacity;
int index;
int *data_p; //指向开辟的堆内存的首地址,作用范围为开辟的单个元素范围
}seqlist_t,*seqlist_p;
c
/**
* @brief 初始化顺序表
* @param int capacity 顺序表的容量大小
* @retval seqlist_p 返回指向创建的顺序表管理结构体的指针
*/
seqlist_p SEQUENTIAL_LIST_Init(int capacity)
{
seqlist_p p;
p=malloc(sizeof(seqlist_t)); //开辟结构体变量类型大小的堆内存
if(p!=NULL) //如果管理结构体内存开辟成功
{
p->data_p=malloc((sizeof(int)*capacity)); //继续开辟存放数据的堆空间内存
p->capacity=capacity; //将传入的capacity容量传给结构体中的capacity
p->index=-1; //下标为-1
if(p->data_p==NULL) //如果开辟存放数据的堆空间内存失败
{
free(p); //释放掉结构体指针指向的堆内存
return NULL; //返回NULL
}
}
else
return NULL; //管理结构体开辟失败
return p; //成功开辟管理结构体并开辟存放数据的堆内存,返回结构体指针。
}
turn p; //成功开辟结构体并开辟存放数据的堆内存,返回结构体指针。
}2.顺序表----增加元素
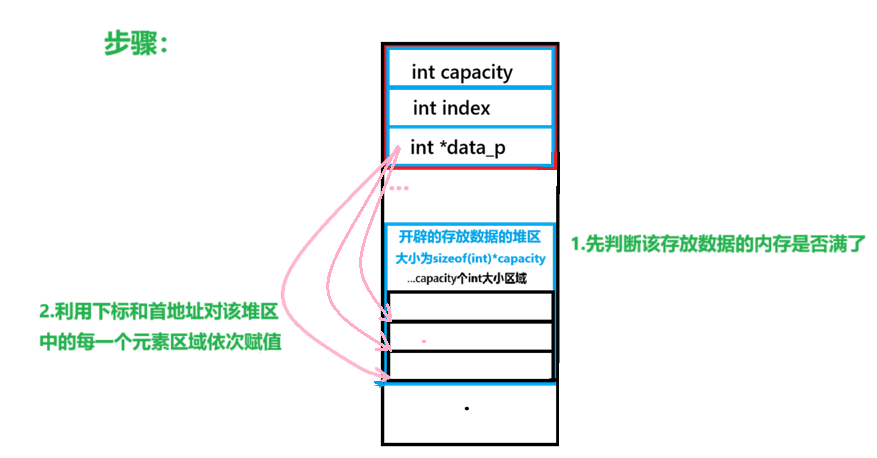
在顺序表已经创建的情况下(一般还会判断顺序表是否是存在的,不存在则跳出函数)
逻辑步骤:
第一步:判断顺序表是否已经存满,存满了就跳出函数并printf打印提醒,未存满则进入第二步。
第二步:顺序表管理结构体中的下标index变量+1(因为在未存放数据时index为-1),并将函数的传入的形参数据赋值给顺序表中相应位置的数据,例如,p->data_p[0]代表顺序表第一个数据。
c
/**
* @brief 增加数据,增加数据在顺序表尾
* @param seqlist_p p 指向顺序表管理结构体的指针
* @param int value 要增加的顺序表的数据值
* @retval int
*/
int SEQUENTIAL_LIST_Add(seqlist_p p,int value)
{
if(SEQUENTIAL_LIST_IsFull(p))
{
printf("顺序表已满!\n");
return -1;
}
//下标+1
p->index=p->index+1;
//增加数据
p->data_p[p->index]=value;
return 0;
}3.顺序表----删除元素
c
/**
* @brief 删除数据,删除后后面的数据往前移
* @param seqlist_p p 指向顺序表管理结构体的指针
* @param int value 要删除的数据值
* @retval int
*/
int SEQUENTIAL_LIST_Del(seqlist_p p,int value)
{
if(SEQUENTIAL_LIST_IsEmpty(p))
{
printf("顺序表已空!!!\n");
return -1;
}
int i=0;
for(i=0;(p->data_p[i]!=value) && (i <= p->index);i++); //遍历到顺序表中和删除的值相同的索引处
if(i <= p->index)
{
for(;i<p->index;i++)
{
p->data_p[i]=p->data_p[i+1];
}
p->index--;
return 0;
}
else
{
printf("顺序表中没有改该值!\n");
return 1;
}
}4.顺序表----查找元素
c
/**
* @brief 查找数据
* @param seqlist_p p 指向顺序表管理结构体的指针
* int value 要查找的数据值
* @retval int
*/
int SEQUENTIAL_LIST_Search(seqlist_p p,int value)
{
for(int i=0;i <= p->index;i++)
{
if(p->data_p[i] == value)
{
printf("找到%d,该数据存在p[%d]中。\n",value,i);
return 0;
}
}
printf("顺序表中没有找到该值!!!\n");
return -1;
}5.顺序表----更改元素
c
/**
* @brief 更改数据
* @param seqlist_p p 指向顺序表管理结构体的指针
* int value 查找的要更改的数据值
* @retval int
*/
int SEQUENTIAL_LIST_Change(seqlist_p p,int value)
{
int change_value;
for(int i=0;i <= p->index;i++)
{
if(p->data_p[i] == value)
{
printf("找到要更改的值,请输入新值:\n");
scanf("%d",&(p->data_p[i]));
return 0;
}
}
printf("未找到要更改的值!!!\n");
return -1;
}三、单向链表(LINK_LIST)
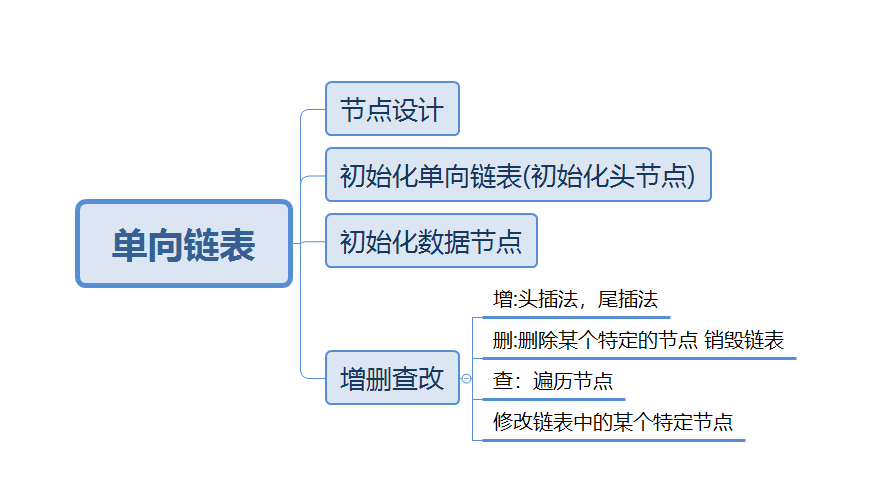
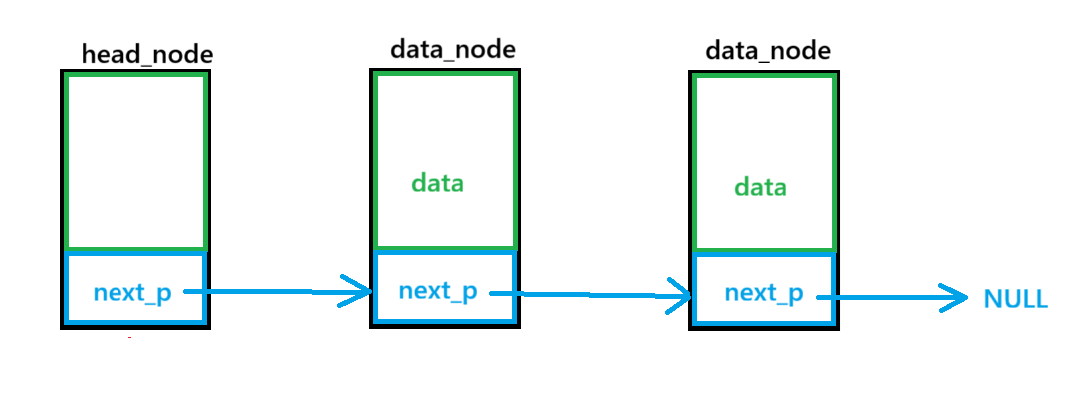
单向链表节点结构体
c
typedef struct node
{
int data; //数据域
struct node* next_p; //指针域
}node_t,*node_p;单链表可以有头节点也可以没有头节点,有头节点便于操作。
单链表头节点不用存数据,只存指向第一个数据节点的指针。
初始化头节点
c
node_p LINK_LIST_InitHeadNode()
{
node_p head=malloc(sizeof(node_t)); //为头节点开辟堆空间,malloc函数返回的是void*
if(head == NULL)
{
printf("头节点开辟堆空间内存失败!\n");
return NULL;
}
else
{
head->next_p=NULL; //单链表头结点的指向空,(NULL)
return head;
}
}初始化数据节点
c
node_p LINK_LIST_InitDataNode(int data)
{
node_p data_node=malloc(sizeof(node_t)); //为数据节点开辟空间
if(data_node == NULL)
{
printf("数据节点开辟堆空间内存失败!");
return NULL;
}
else
{
data_node->data=data;
data_node->next_p=NULL;
return data_node;
}
}(头插法/尾插法)添加数据节点
函数参数:添加数据节点到单链表中,首先需要明确是哪条单链表,因此需要单链表的头节点 ,其次需要要添加的该数据节点,因此函数的参数便确定了。
头插法函数操作:需要插入在单链表的头节点后面。(这一步需要判断头节点的next_p是否为空),即将要添加的数据节点的next_p指向头节点当前指向的下一个数据节点(即所有数据节点中当前的第一个),再将头节点指向新添加的数据节点。
尾插法函数操作:需要插入在单链表的最后。查找最后一个节点(需要在函数内部定义一个临时节点指针用于遍历)从头节点开始依次遍历直到遍历到的节点的next_p等于NULL(该节点即为单链表的最后一个节点)(不需要判断头节点是否为空是因为从头节点开始遍历判断包含了只有头节点的单链表情况)。将遍历到的节点的next_p指向要添加的节点。
返回值:无。
头插法:
c
void LINK_LIST_HeadInsert(node_p head,node_p data_node)
{
if((head == NULL) || (data_node == NULL))
{
printf("传入的参数为空!\n");
return ;
}
if(head->next_p == NULL) //判断头节点的next_p是否为空,如果为空则代表该链表是一个只有头节点无数据节点的单链表,即将加入第一个数据节点
{
head->next_p = data_node;
}
else //单链表的除头节点外还有其他数据节点
{
data_node->next_p = head->next_p; //将要添加的数据节点的next_p指向当前链表的第一个数据节点
head->next_p =data_node; //将头节点的next_p指向加入的数据节点
}
}尾插法:
c
void LINK_LIST_TailInsert(node_p head,node_p data_node)
{
if((head == NULL) || (data_node == NULL))
{
printf("传入的参数为空!\n");
return ;
}
node_p tmp=head;
for(;tmp->next_p != NULL;tmp = tmp->next_p); //定义一个临时节点变量用于遍历,并赋值从头节点开始判断该节点的next_p为NULL时退出遍历。
tmp->next_p = data_node; //将要遍历到的数据的next_p指向要添加的数据
}删除数据节点
删除数据节点可以有很多种删除方法,可以删除最后一个节点, 删除数据相关的节点,删除处于某个位置的节点,限于篇幅,我们这里删除对应数据的节点。
参数:头节点 要删除的数据值(数据节点数据域存储的值)
c
void LINK_LIST_DeleteData(node_p head,int data)
{
if(head == NULL)
{
printf("传入的head参数为空!\n");
return ;
}
node_p tmp=head; //定义一个tmp并赋值头节点
for(;(tmp->next_p != NULL)&&(tmp->next_p->data != data);tmp=tmp->next_p); //遍历单链表,判断tmp的下一个数据节点中的数据值是否是要删除的数据并且判断tmp不为最后一个节点,否则停止遍历
if(tmp->next_p == NULL) //tmp遍历停止后,对其进行具体判断是否是因为遍历完了才停止的
{
printf("该单链表中无要删除的数据!\n");
return ; //退出函数
}
node_p del_p=tmp->next_p; //将要删除的数据节点的地址保存起来便于后续销毁堆内存
tmp->next_p=tmp->next_p->next_p; //将tmp的next_p指向后一个数据节点的next_p,即进行跳跃指向
del_p->next_p = NULL; //将dep_p的next_p指向NULL
free(del_p); //释放掉del_p内存
}查找数据节点
根据数据查该数据节点的位置,根据数据节点查找数据,或者根据数据查另一些数据。
本质上就是将单链表遍历。
c
void LINK_LIST_Serch(node_p head,int data)
{
if(head == NULL)
{
printf("传入的head参数为空!\n");
return ;
}
node_p tmp=head->next_p; //定义一个临时变量从数据节点中的第一个开始遍历
for(int i=0;tmp != NULL;tmp=tmp->next_p,i++) //从第一个数据节点开始遍历并记录位置
{
if(tmp->data == data)
{
printf("该链表中有data数据,位于链表数据节点中第%d个",i);
return ;
}
}
printf("该链表中无data数据!\n");
}更改数据节点
c
void LINK_LIST_Change(node_p head,int chang_data,int data)
{
if(head->next_p == NULL)
{
printf("该链表为空链表!\n");
return ;
}
node_p tmp=head->next_p;
for(;tmp != NULL;tmp = tmp->next_p) //遍历单链表
{
if(tmp->data == change_data) //找到要修改的数据
{
tmp->data=data; //替换为修改后的数据
return ;
}
}
}遍历单链表数据
c
void LINK_LIST_Show(node_p head)
{
if(head == NULL)
{
printf("传入head参数为空!\n");
return ;
}
if(head->next_p != NULL)
{
printf("该链表是空链表!\n");
return ;
}
node_p tmp = head->next_p;
printf("***************单链表数据***************\n");
for(int i=0;tmp != NULL;tmp = tmp->next_p,i++)
{
printf("第%d个数据节点的数据是%d\n",i,tmp->data);
}
printf("***************单链表数据***************\n");
}销毁单链表
c
node_p LINK_LIST_Destroy(node_p head)
{
if(head == NULL)
{
printf("传入head参数为空!\n");
return NULL;
}
node_p tmp1=head,tmp2=tmp1->next_p;
for(;tmp1 != NULL;tmp1 = tmp2,tmp2=tmp1->next_p)
{
tmp1->next_p=NULL;
free(tmp1);
}
return NULL;
}四、双向链表(DLINK_LIST)
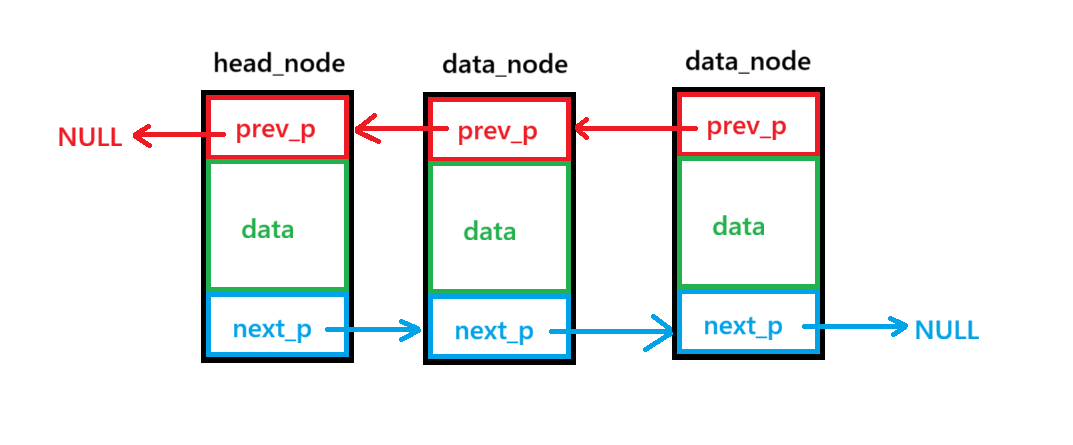
双向链表结构体
c
typedef struct node
{
struct node* prep_p; //指向前一个节点的指针
int data; //数据域
struct node* next_p; //指向后一个节点的指针
}node_t,*node_p;初始化头节点
c
node_p DLINK_LIST_InitHeadNode()
{
node_p head = malloc(sizeof(node_t));
if(head == NULL)
{
printf("头节点开辟堆空间内存失败!\n");
return NULL;
}
head->prep_p = NULL;
head->next_p = NULL;
return head;
}初始化数据节点
c
node_p DLINK_LIST_InitDataNode(int data)
{
node_p data_node = malloc(sizeof(node_t));
if(data_node == NULL)
{
printf("数据节点开辟堆空间内存失败!\n");
return NULL;
}
data_node->prep_p = NULL;
data_node->next_p = NULL;
return data_node;
}(头插法\尾插法)增加数据节点
头插法:
c
void DLINK_LIST_HeadInsert(node_p head,node_p data_node)
{
if((head == NULL) || (data_node == NULL))
{
printf("传入参数为空!\n");
return ;
}
data_node->prep_p = head; //将要加入的数据节点的prep_p指向头节点
data_node->next_p = head->next_p; //将要加入的数据节点的next_p指向第一个数据节点(或者是head本身)
head->next_p->prep_p = data_node; //将第一个数据节点(或则是head头节点)的prep_p指向要加入的数据节点
head->next_p = data_node; //将头节点的next_p指向要加入的数据节点
}尾插法:
c
void DLINK_LIST_TailInsert(node_p head,node_p data_node)
{
if((head == NULL) || (data_node == NULL))
{
printf("传入参数为空!\n");
return ;
}
node_p tmp = head;
for(;tmp->next_p != NULL;tmp = tmp->next_p); //遍历到最后一个数据节点
tmp->next_p = data_node; //将最后一个数据节点的next_p指向要加入的数据节点
data_p->prep_p = tmp; //将要加入的数据节点的prep_p指向最后一个数据节点
}删除数据节点
c
void DLINK_LIST_DeleteData(node_p head,int data)
{
if(head == NULL)
{
printf("传入的head参数为NULL!\n");
return ;
}
node_p tmp1=head,tmp2=tmp1->next_p; //一个用于保存前驱节点信息并遍历,一个用于删除节点(释放被删除节点的内存)
for(;tmp2 != NULL;)
{
if(tmp2->data == data)
{
tmp1->next_p = tmp2->next_p;
tmp2->next_p->prep_p = tmp1;
tmp2->next_p = NULL;
tmp2->prep_p = NULL;
free(tmp2);
return ;
}
}
printf("未在该双向链表中找到该数据节点!\n");
}双向链表的查找和更改基本上和单链表的查找和更改函数无区别,当然双向链表可以单独设定从后往前遍历
查找数据节点
c
void DLINK_LIST_Serch(node_p head,int data)
{
if(head == NULL)
{
printf("传入的head参数为空!\n");
return ;
}
node_p tmp = head->next_p; //定义一个临时变量从数据节点中的第一个开始遍历
for(int i=0;tmp != NULL;tmp=tmp->next_p,i++) //从第一个数据节点开始遍历并记录位置
{
if(tmp->data == data)
{
printf("该链表中有data数据,位于链表数据节点中第%d个",i);
return ;
}
}
printf("该链表中无data数据!\n");
}更改数据节点
c
void DLINK_LIST_Change(node_p head,int chang_data,int data)
{
if(head->next_p == NULL)
{
printf("该链表为空链表!\n");
return ;
}
node_p tmp=head->next_p;
for(;tmp != NULL;tmp = tmp->next_p) //遍历单链表
{
if(tmp->data == change_data) //找到要修改的数据
{
tmp->data=data; //替换为修改后的数据
return ;
}
}销毁双向链表
c
void destroy(node_p head)
{
if(head == NULL)
{
printf("传入的head参数为NULL!\n");
return ;
}
node_p tmp1 = head,tmp2 = tmp1->next_p; //销毁需要两个指针,一个用于销毁当前节点,一个存储后一个节点地址用以遍历.当然也有只用一个指针的写法,个人喜好
for(;tmp1 != NULL;tmp1 = tmp2,tmp2=tmp->next_p)
{
tmp1->next_p = NULL;
tmp1->prep_p = NULL;
free(tmp1);
}
}循环链表(双向循环链表为例)
末尾的next_p重新指向head_node,而head_node的prev_p指向数据节点最后的data_node节点
结构体不变,但是在初始化头节点,增删时会有所不同。
其余函数不同主要在于遍历判断不再是判断next_p 是否等于 NULL, 而是判断next_p 是否等于 head。
双向循环链表头节点:
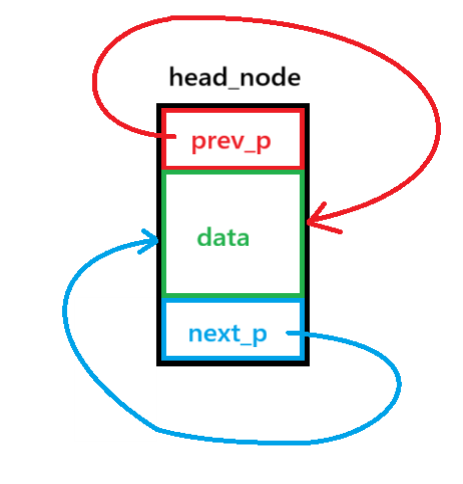
初始化循环链表
c
node_p CIR_DLINK_LIST_InitHeadNode()
{
node_p head = malloc(sizeof(node_t));
if(head == NULL)
{
printf("头节点开辟堆空间内存失败!\n");
return ;
}
head->prep_p = head; //双向循环链表的头节点的prep_p指向自己
head->next_p = head; //双向循环链表的头节点的next_p指向自己
}双向循环链表:
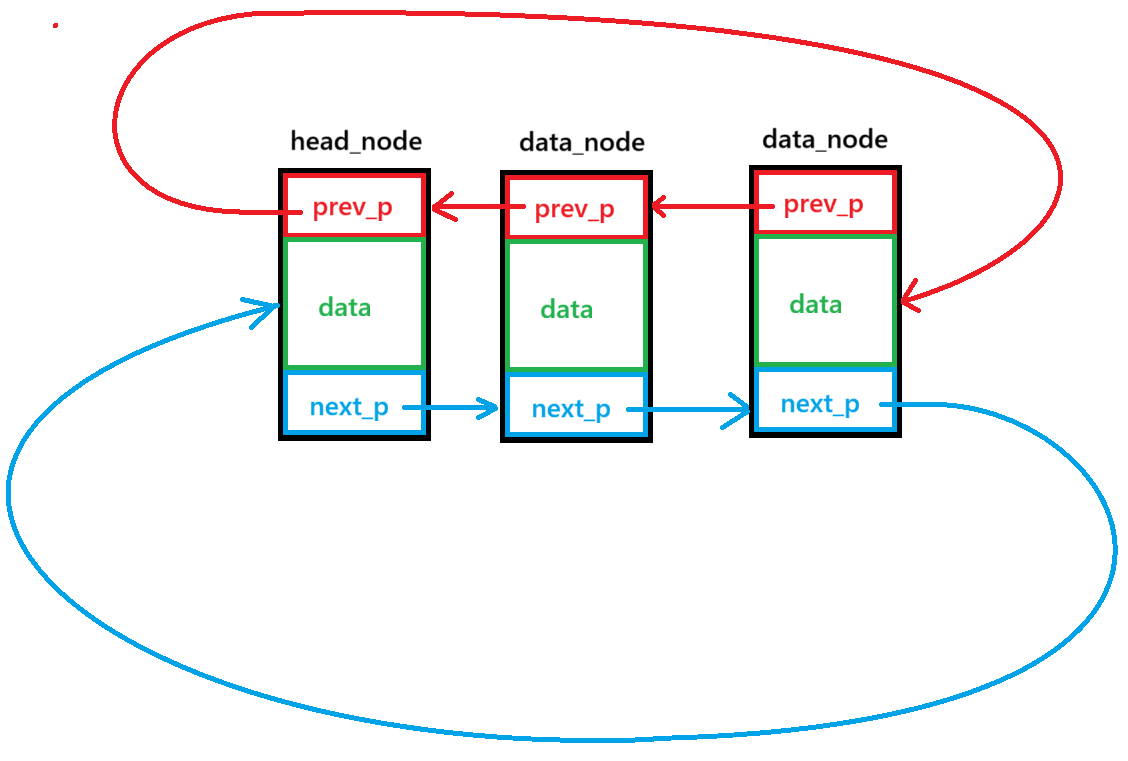
增加数据节点
头插法:
c
void CIR_DLINK_LIST_HeadInsert(node_p head,node_p data_node)
{
if(head == NULL || data_node == NULL)
{
printf("传入的参数为NULL!\n");
return ;
}
node_p tmp = head->next_p; //这里可以不用定义变量保存。
//(如果不用的话,将下面四行代码tmp换成head->next_p即可,但是需要注意的是以下四行的代码最好不要调换顺序赋值,否则会导致错误)
data_node->next_p = tmp; //将要加入的数据节点的next_p指向头节点的下一个节点
data_node->prep_p = head; //将要加入的数据节点的prep_p指向头节点的上一个节点
tmp->prep_p = data_node; //将保存的头节点的下一个节点的prep_指向要加入的节点
head->next_p = data_node; //将头节点的next_p指向要加入的数据节点
}尾插法:
c
void CIR_DLINK_LIST_TailInsert(node_p head,node_p data_node)
{
if(head == NULL || data_node == NULL)
{
printf("传入的参数为NULL!\n");
return ;
}
node_p tmp =head;
for(;tmp->next_p != head;tmp = tmp->next_p); //遍历到最后一个数据节点,注意判断条件不再是NULL
tmp->next_p = data_node; //将最后一个数据节点的next_p指向要加入的数据节点
data_node->prep_p = tmp; //将要加入的数据节点的prep_p指向最后一个数据节点
data_node->next_p = head; //将数据节点的next_p指向头节点
head->prep_p = data_node; //将头节点的prep_p指向要加入的数据节点
}删除数据节点
c
void CIR_DLINK_LIST_Delete(node_p head,int data)
{
if(head == NULL)
{
printf("传入的head参数为NULL!\n");
return ;
}
node_p tmp1 = head->next_p;
for(;tmp1 != head; tmp1 = tmp1->next_p)
{
if(tmp1->data == data)
{
node_p tmp2 = tmp1->prep_p; //找到当前节点为要删除的节点,保存当前节点的前驱节点地址
tmp2->next_p = tmp1->next_p; //将前驱节点的next_p指向tmp的下一个节点
tmp1->next_p->prep_p =tmp2; //将tmp1的下一个节点的prep_p指向tmp2
tmp1->next_p = NULL;
tmp1->prep_p = NULL;
free(tmp1);
return ;
}
}
printf(在该链表中未找到该数据!\n");
}掌握了顺序表,链表。栈,和队列写起来就非常轻松了,因为他们只是在链表和顺序表的基础上输入输出上有特定的规则,比如栈先进后出,后进先出。
五、栈
顺序栈(SEQUENTIAL_STACK)
顾名思义,顺序结构的栈。牢记一点即可,顺序结构都是利用"数组",这个数组是需要我们自己在堆空间开辟的。
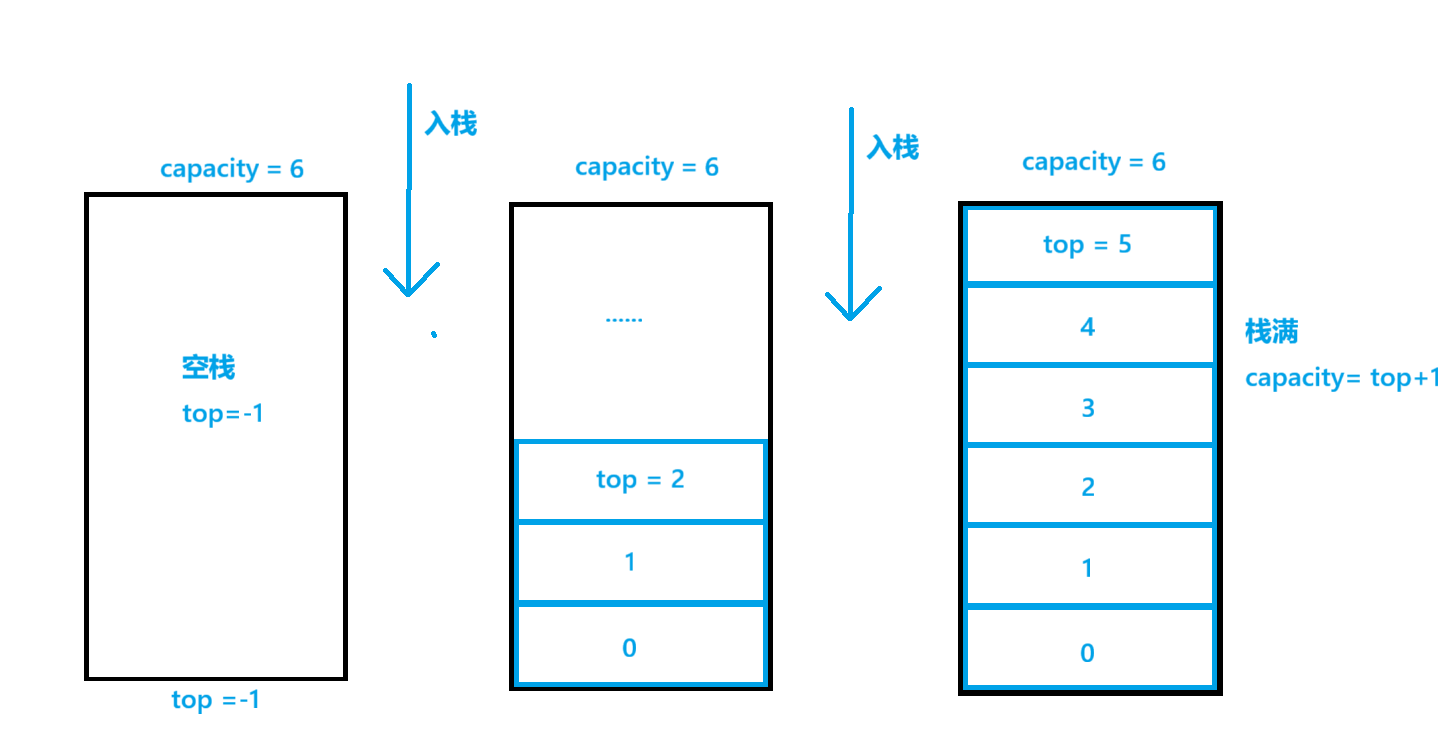
栈管理结构体
c
typedef struct seq_stack
{
int capacity; //存储顺序栈容量便于开辟空间
int top; //栈顶位置,用于增删元素
int * data_p; //数据地址,作用范围为一个数据
}seq_stack_t,*seq_stack_p;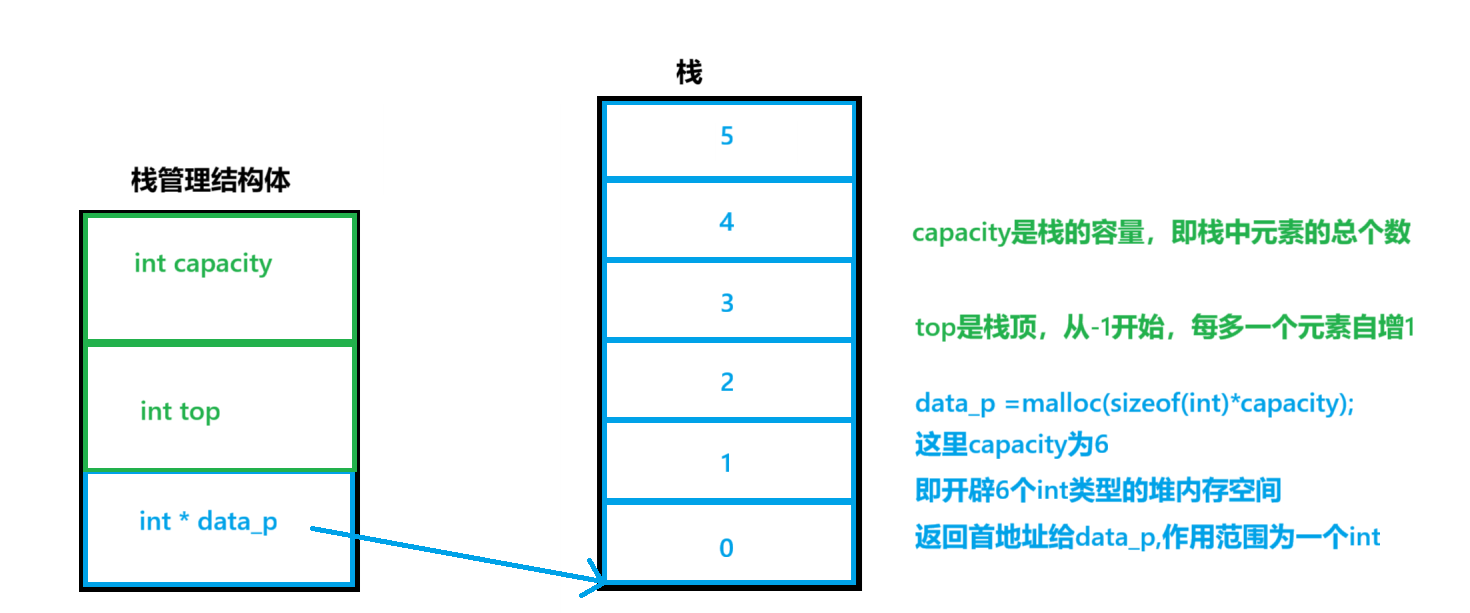
初始化栈
c
seq_stack_p SEQUENTIAL_STACK_Init(int capacity)
{
seq_stack_p stack_p = malloc(sizeof(seq_stack_t)); //为管理结构体开辟堆内存空间
if(stack_p == NULL)
{
printf("管理结构体开辟堆内存空间失败!\n");
return ;
}
stack_p->capacity = capacity;
stack_p->top = -1;
stack_p->data_p = malloc(sizeof(int) * capacity);
if(stack_p->data->p == NULL)
{
printf("管理结构体开辟堆内存空间失败!\n");
free(stack_p);
return NULL;
}
return stack_p;
}判断栈满
c
bool SEQUENTIAL_STACK_IfFull(seq_stack_p stack_p)
{
return stack_p->top == stack_p->capacity-1;
}判断栈空
c
bool SEQUENTTIAL_STACK_IfEmpty(seq_stack_p stack_p)
{
return stack_p->top == -1;
}入栈
c
int SEQUENTIAL_STACK_Push(seq_stack_p stack_p,int data)
{
if(stack_p == NULL || stack_p->data_p == NULL)
{
printf("stack_p为NULL!或者栈管理结构体里的data_p为NULL\n");
return -1;
}
if(!SEQUENTIAL_STACK_IfFull(stack_p)) //栈不满
{
stack_p->top +=1; //栈顶+1
stack_p->data_p[stack_p->top] = data; //数据入栈
return 0;
}
else
{
printf("栈满,无法入栈!\n");
return -1;
}
}出栈
c
int SEQUENTIAL_STACK_Pop(seq_stack_p stack_p)
{
if(stack_p == NULL)
{
printf("传入的stack_p参数为NULL!\n");
return -1;
}
if(!SEQUENTTIAL_STACK_IfEmpty(stack_p))
{
stack_p->top-=1; //栈顶-1,不用理会里面的数据,入栈时会覆盖
return 0;
}
else
{
printf("空栈!\n");
return -1;
}
}链式栈(LINK_STACK)
栈节点结构体
c
typedef struct stack_node
{
int data; // 数据域
struct stack_node * next_p; //指针域
}stack_node_t,*stack_node_p;栈管理结构体
c
typedef struct link_stack
{
int num; //用于计数,链表中有多少个数据
stack_node_p top_p; //top指针,指向栈链表数据节点
}link_stack_t,*link_stack_p;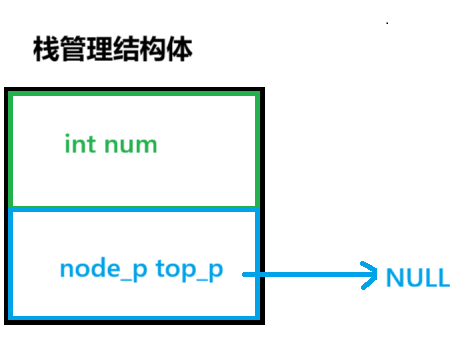
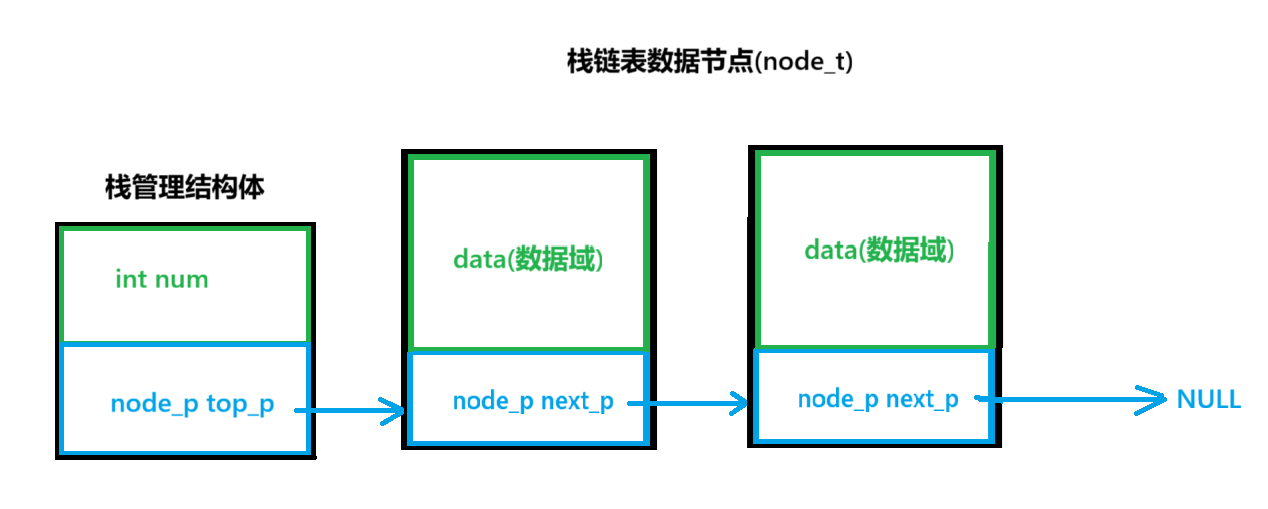
初始化栈链表
c
link_stack_p LINK_STACK_StackInit()
{
link_stack_p stack_p = malloc(sizeof(link_stack_t));
if(stack_p == NULL)
{
printf("链式栈管理结构体开辟内存失败!");
return NULL;
}
stack_p->num = 0;
stack_p->top_p = NULL;
return stack_p;
}初始化栈链表数据节点
c
node_p LINK_STACK_NodeInit(int data)
{
stack_node_p node_p = malloc(sizeof(node_t));
if(node_p == NULL)
{
printf("链式栈节点开辟堆内存空间失败!");
return NULL;
}
node_p->next_p = NULL;
node_p->data = data;
}入栈
c
void LINK_STACK_Push(link_stack_p stack_p,stack_node_p node_p)
{
stack_node_p tmp = stack_p->top_p;
stack_p->num = stack_p->num + 1;
node_p->next_p = tmp;
stack_p->top_p = node_p;
}出栈
c
void LINK_STACK_Pop(link_stack_p stack_p)
{
stack_node_p tmp=stack_p->top_p;
stack_p->num--;
stack_p->top_p = tmp->next_p;
tmp->next_p = NULL;
}六、队列(queue)
队列的特征是先进先出。队尾入队,队头出队。
顺序循环队列
顺序结构的队列,顺序结构的队列管理结构体应包含队头,队尾,容量,指向存储队列数据内存的地址。
顺序队列的满队列和实际意义上内存的满队列不同。
顺序队列的满队列需要预留一个元素位置用以区分判断空队列的情况。
(详情见下图满队列和空队列的区别)
如果不这么做,就会出现满队列的判断条件为rear = front , 空队列的判断条件也为rear = front.
(当然也有不用预留的方法需要多添加一个num的变量用以记录存取了多少个数据,如果和capacity相同则为满栈,为0则为空栈)
队列管理结构体
c
typedef struct queue{
int capacity; //容量
int front; //队头
int rear; //队尾
int * data_p; //数据内存指针
}queue_t,*queue_p;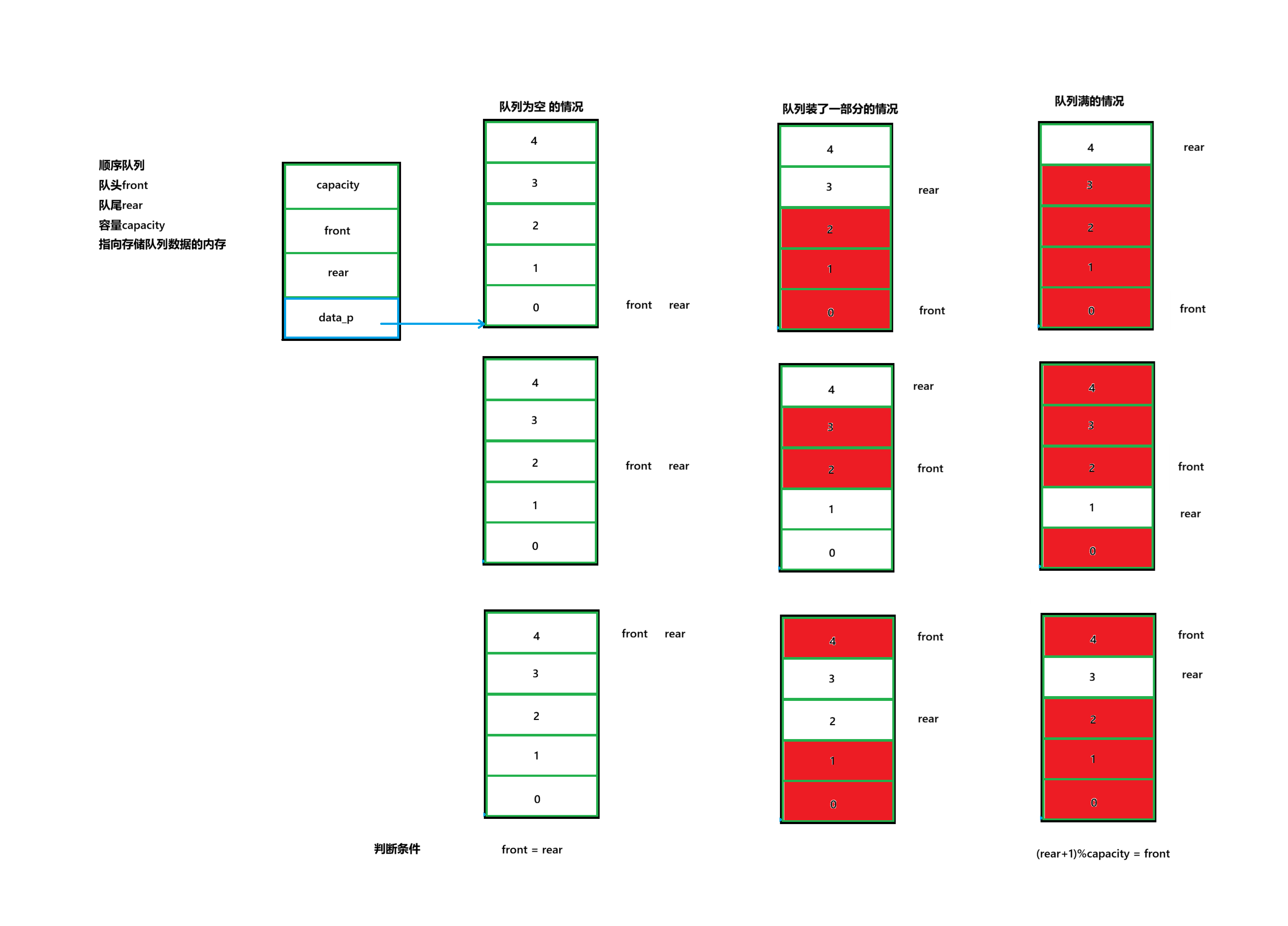
初始化队列
c
queue_p SEQUENTIAL_QUEUE_Init(int capacity)
{
queue_p p = malloc(sizeof(queue_t));
if(p == NULL)
{
printf("队列开辟堆内存失败!\n");
return NULL;
}
p->data_p = malloc(sizeof(int)*capacity);
if(p->data_p == NULL)
{
printf("队列开辟堆内存失败!\n");
free(p);
return NULL;
}
p->front = 0; //队头初始为0
p->rear = 0; //队尾初始为0
p->capacity = capacity;
return p;
}判断队满
c
bool SEQUENTIAL_QUEUE_IfFull(queue_p queue)
{
if((queue->rear+1)%capacity == front)
return true;
else
return false;
}判断队空
c
bool SEQUENTIAL_QUEUE_IfEmpty(queue_p queue)
{
if(queue->rear == queue->front)
return true;
else
return false;
}入队
c
void SEQUENTIAL_QUEUE_En(queue_p queue,int data)
{
if(!SEQUENTIAL_QUEUE_IfFull(queue))
{
queue->data_p[queue->rear] = data;
queue->rear = (queue->rear + 1) % queue->capacity;//队尾+1余容量 队尾入队
}
else
{
printf("队列已满!\n");
}
}出队
c
void SEQUENTIAL_QUEUE_Out(queue_p queue)
{
if(!SEQUENTIAL_QUEUE_IfEmpty(queue))
{
queue->front = queue->(front+1) % capacity; //队头+1余容量 队头出队
}
else
{
printf("队列为空!\n");
}
}链式队列
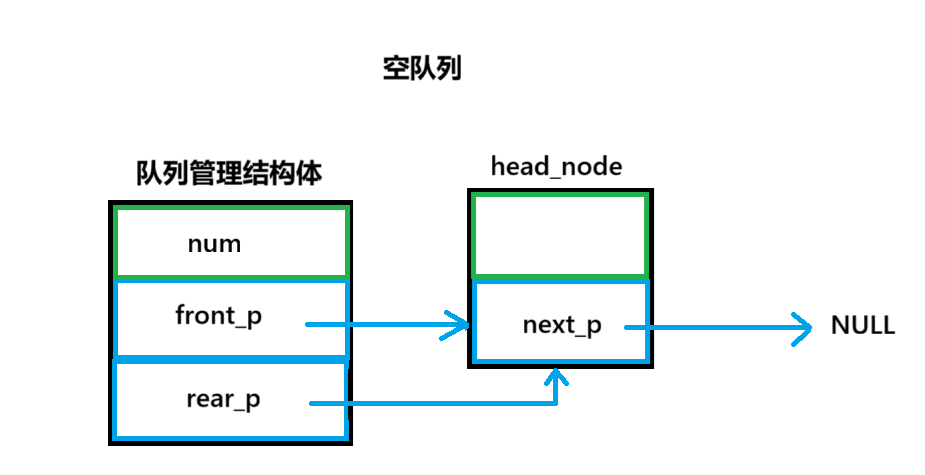
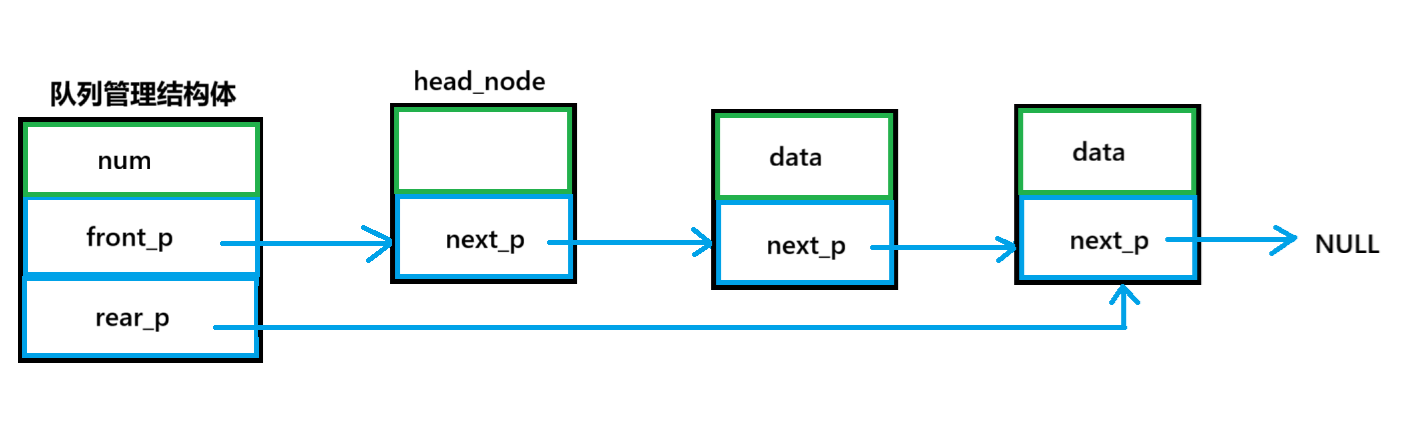
数据节点结构体
c
typedef struct node
{
int data; //数据域
struct node * next_p;
}node_t, *node_p;队列管理结构体
c
typedef struct queue
{
int num;
node_p front_p; //队头指针
node_p rear_p; //队尾指针
}queue_t, *queue_p;初始化头节点
c
node_p LINK_QUEUE_InitHeadNode()
{
node_p head = malloc(sizeof(node_t));
if(head == NULL)
{
printf("头节点开辟失败!\n");
return NULL:
}
head->next_p = NULL;
rertun head;
}初始化队列
c
queue_p LINK_SQUEUE_Init(node_p head)
{
queue_p p = malloc(sizeof(queue_t));
if(p == NULL)
{
printf("队列开辟堆内存失败!\n");
return NULL;
}
node_p head = malloc(sizeof(node_t));
if(head == NULL)
{
printf("头节点开辟堆内存失败!\n");
free(p);
return NULL;
}
head->next_p = NULL; //初始化next_p指针
p->num = 0;
p->front_p = head; //初始化front_p指针
p->rear_p = head; //初始化rear_p指针
return p;
}初始化数据节点
c
node_p LINK_QUEUE_InitNode(int data)
{
node_p node = malloc(sizeof(node_t));
if(node == NULL)
{
printf("数据节点开辟失败!\n");
return NULL:
}
node->data = data;
node->next_p = NULL;
rertun node;
}入队
c
void LINK_QUEUE_En(queue_p p,node_p node)
{
if(p == NULL || node == NULL)
{
printf("传入的参数为NULL!\n");
retrun ;
}
p->rear_p ->next_p = node; //直接将队尾的next_p指针指向新节点
p->rear_p = node; //并将队尾指针指向新节点,作为新的队尾
}出队
c
void LINK_QUEUE_Out(queue_p p,node_p node)
{
if(p == NULL || node == NULL)
{
printf("传入的参数为NULL!\n");
retrun ;
}
node_p delnode = p->front_p->next_p; //定义一个临时的delnode存储要删除的节点
p->front_p->next_p = delnode->next_p; //将头节点节点中的next_p指向要删除节点后的一个数据节点
delnode->next_p = NULL; //将数据节点的next_p置为NULL
free(delnode); //释放掉delnode的内存
}七、二叉树(Binary Tree)与BST(Binary Search Tree)二叉搜索树
数据结构:
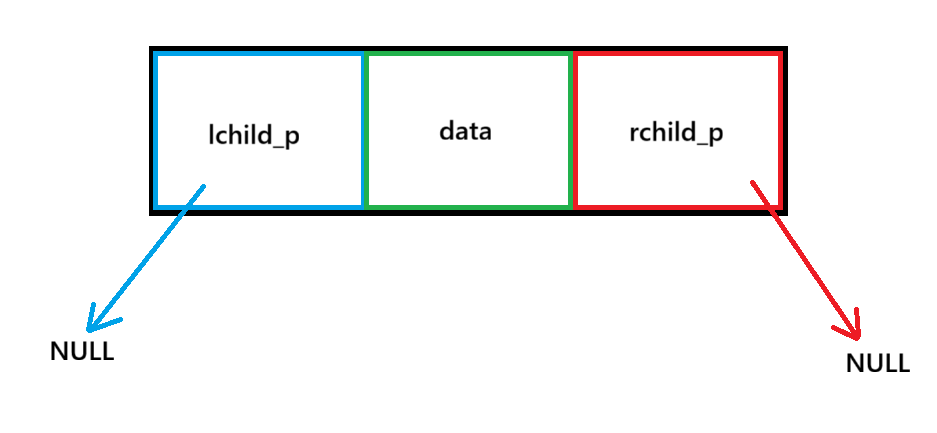
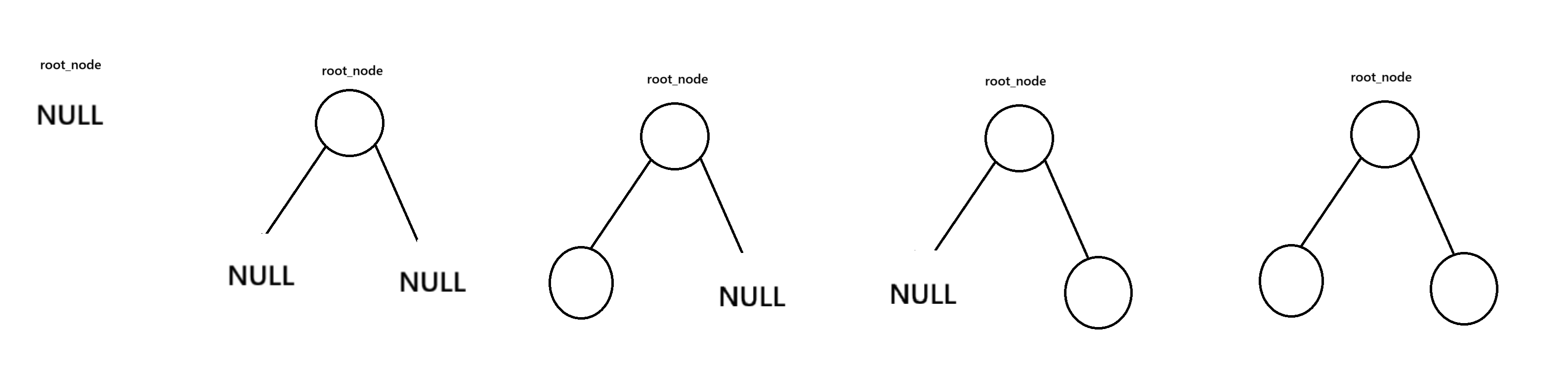
c
typedef struct node
{
int data;
struct node * lchild_p; //指向左子树的指针
struct node * rchild_p; //指向右子树的指针
}node_t,*node_p;
c
node_p BST_InitDataNode(int data)
{
node_p new_node = malloc(sizeof(node_t));
if(new_node == NULL)
{
printf("开辟节点失败!\n");
return NULL;
}
new_node->lchild_p = NULL;
new_node->rchild_p = NULL;
new_node->data = data;
return new_node;
}BST逻辑:
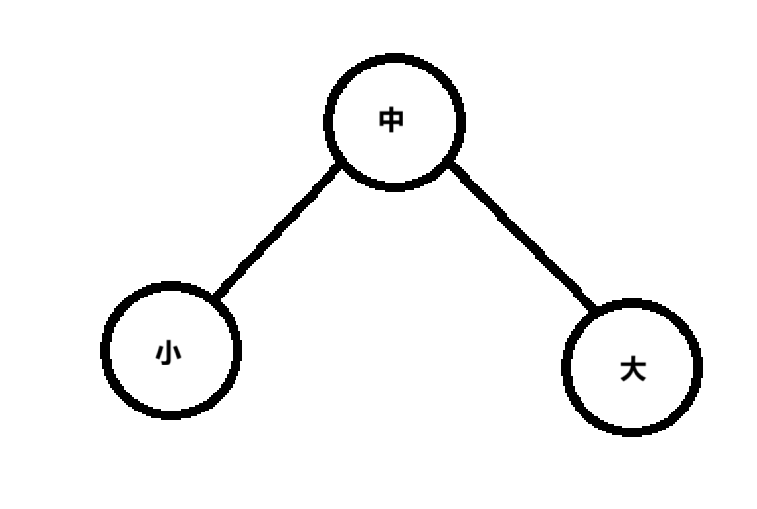
例子:
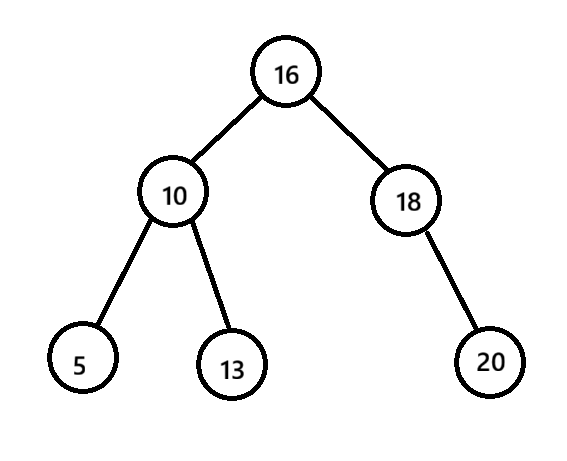
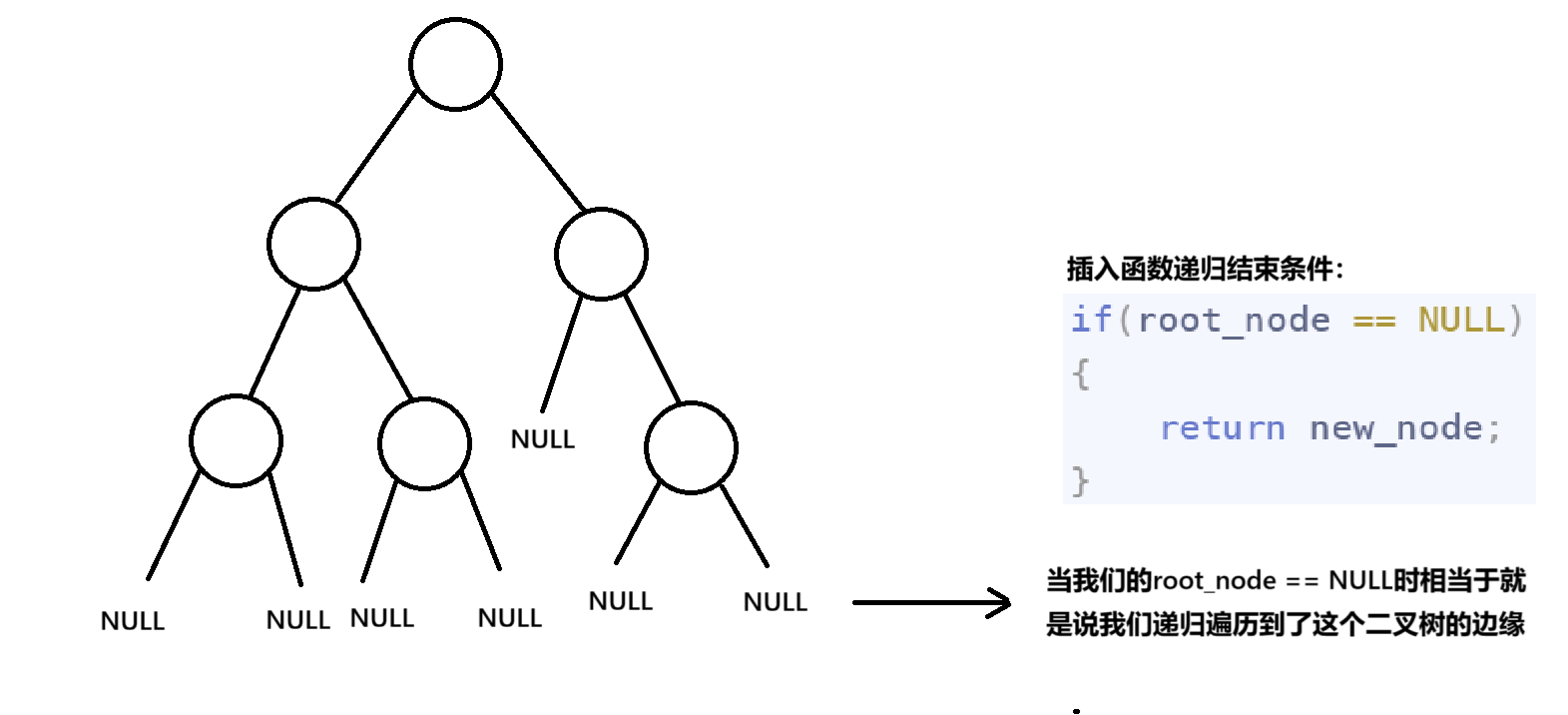
插入节点

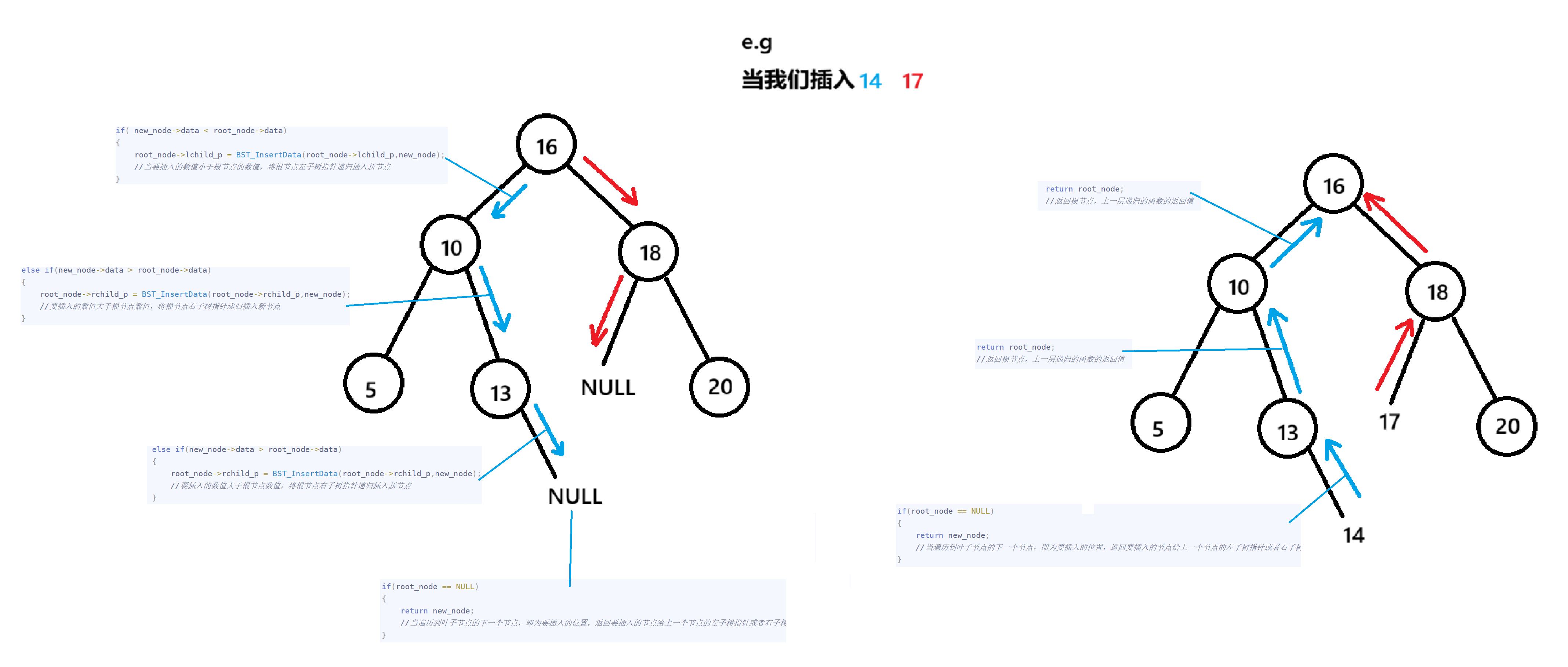
c
node_p BST_InsertData(node_p root_node,node_p new_node)
{
if(root_node == NULL)
{
return new_node;
//当遍历到叶子节点的下一个节点,即为要插入的位置,返回要插入的节点给上一个节点的左子树指针或者右子树指针
}
if( new_node->data < root_node->data)
{
root_node->lchild_p = BST_InsertData(root_node->lchild_p,new_node);
//当要插入的数值小于根节点的数值,将根节点左子树指针递归插入新节点
}
else if(new_node->data > root_node->data)s
{
root_node->rchild_p = BST_InsertData(root_node->rchild_p,new_node);
//要插入的数值大于根节点数值,将根节点右子树指针递归插入新节点
}
else
{
printf("该二叉树中已有重复数据!请重新输入\n");
free(new_node);
}
return root_node;
//返回根节点,上一层递归的函数的返回值
}遍历节点
遍历节点常用的方式有前序遍历,中序遍历,后序遍历等
c
//前序遍历 根左右
void BST_PreorderTraverse(node_p root_node)
{
if(root_node == NULL)
return ;
printf("%d\t",root_node->data);
BST_PreorderTraverse(root_node->lchild_p);
BST_PreorderTraverse(root_node->rchild_p);
}
//中序遍历 左根右
void BST_InorderTraverse(node_p root_node)
{
if(root_node == NULL)
return ;
BST_InorderTraverse(root_node->lchild_p);
printf("%d\t",root_node->data);
BST_InorderTraverse(root_node->rchild_p);
}
//后序遍历 左右根
void BST_PosorderTraverse(node_p root_node)
{
if(root_node == NULL)
return ;
BST_PosorderTraverse(root_node->lchild_p);
BST_PosorderTraverse(root_node->rchild_p);
printf("%d\t",root_node->data);
}删除节点
找到要删除的节点,按一定规则删除节点并按BST的规则排列二叉树。
要删除的数据比根节点数据小,左子树递归
要删除的数据比根节点数据大,右子树递归
要删除的数据等于根节点数据,删除节点
若删除的节点有左子树,将左子树的最大值复制到删除节点,并删除左子树最大值。
若删除的节点有右子树,将右子树的最小值复制到删除节点,并删除右子树最小值
栗子:删除12
1.找到要删除的节点数值,(如果有左子树节点)并在其左子树中遍历找出最大值(最大值一定在该左子树中的右节点中)
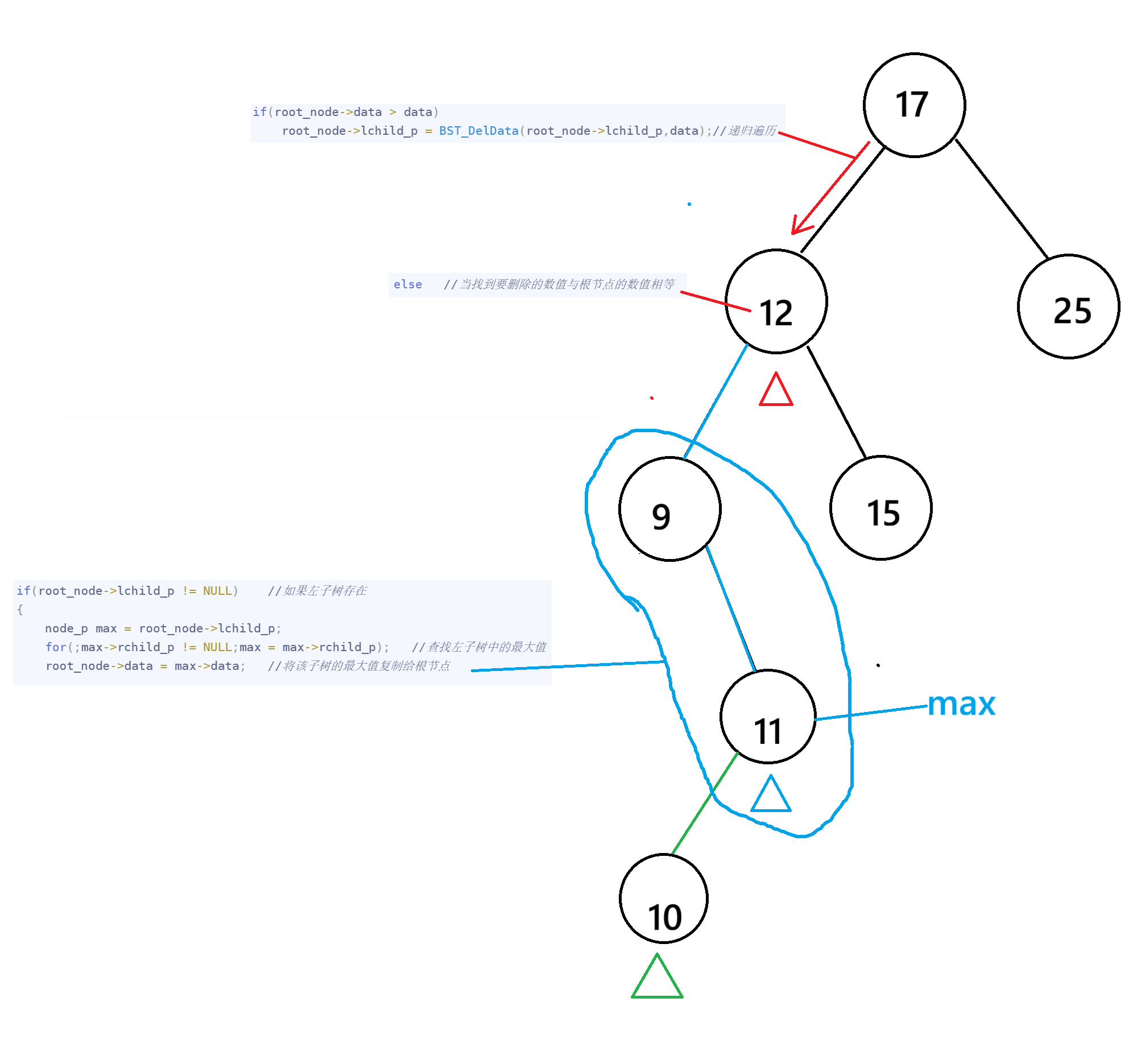
2.将该左子树的最大值复制给根节点,并递归删除该最大值max
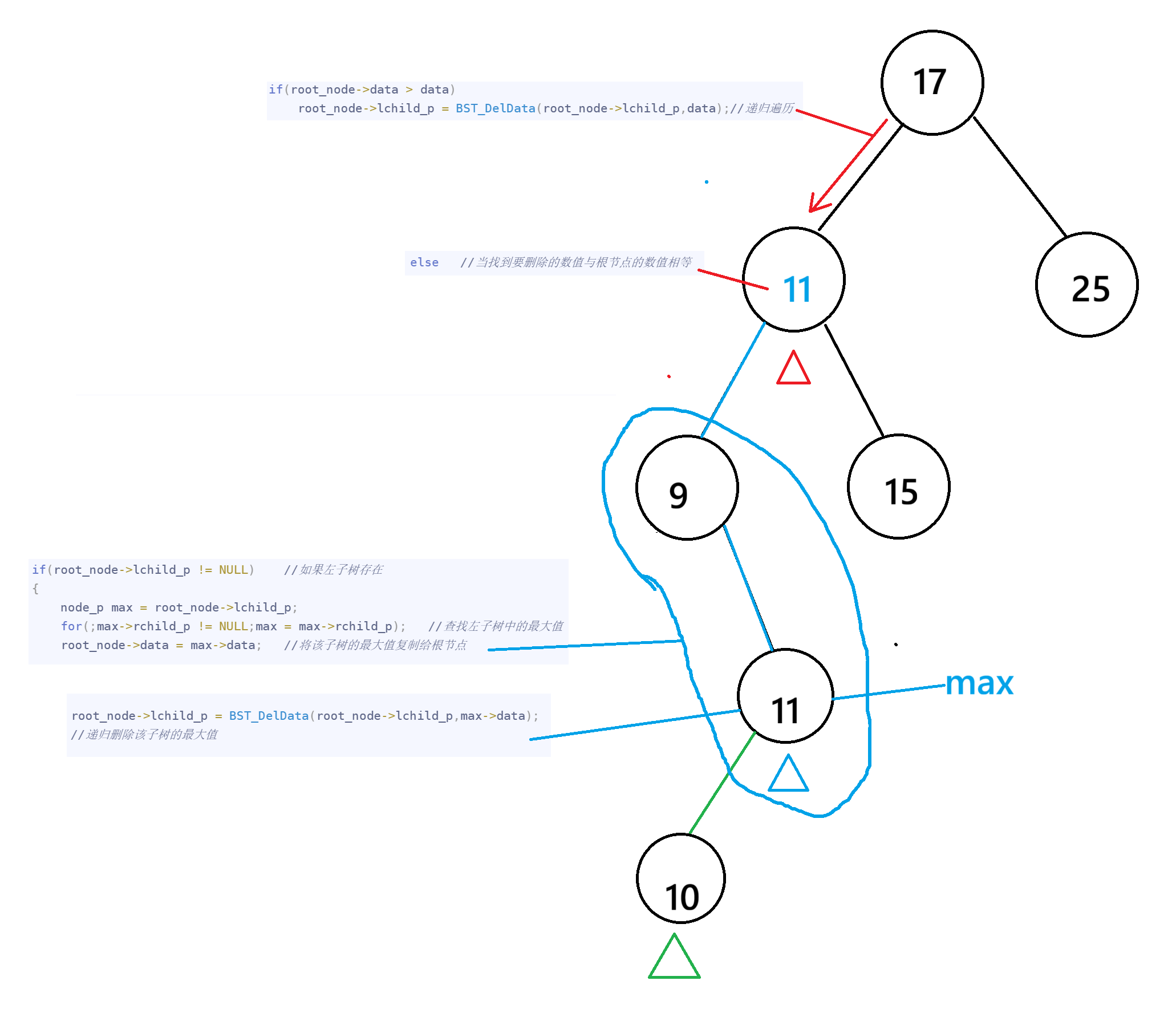
3.将该最大值11的左子树节点的最大值10赋值给根节点11,同时递归删除10,叶子节点10无左子树也无右子树,因此释放内存并返回NULL给根节点10的左子树指针。
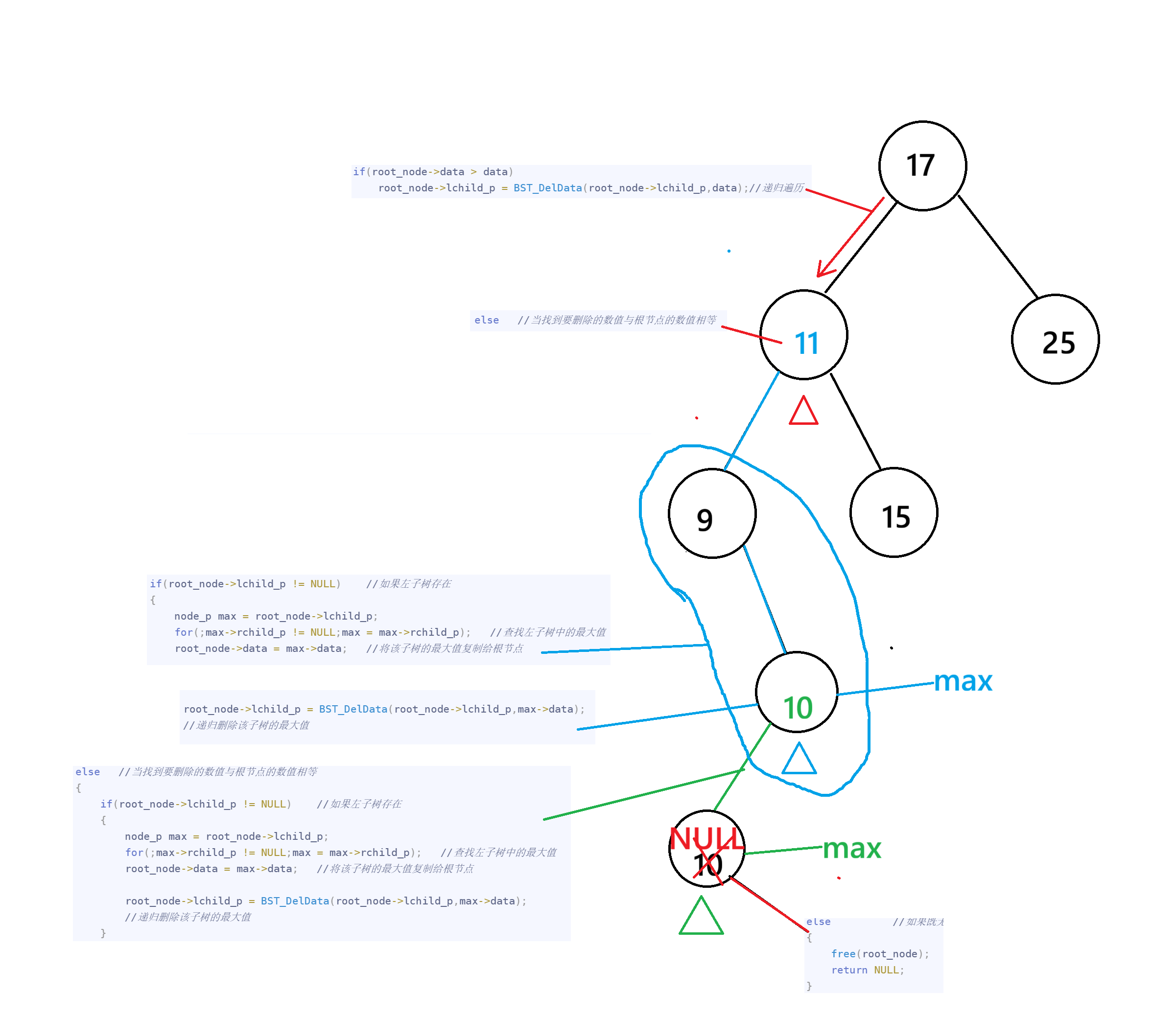
注意:
1.当跟节点为NULL时说明递归遍历到了二叉树的边缘,此时会开始返回值
2.替换左子树最大值和右子树最小值都可以实现删除,具体优先替换谁,依个人喜好。
3.当找到要删除的节点后,根节点无左子树时,会查找右子树最小值,而当两者都没时会删除节点,这里不能 连用3个if判断,只能用if...else if ...else
c
node_p BST_DelData(node_p root_node,int data)
{
if(root_node == NULL)
return NULL; //遍历到二叉树的边缘
if(root_node->data > data)
root_node->lchild_p = BST_DelData(root_node->lchild_p,data);//递归遍历
else if(root_node->data < data)
root_node->rchild_p = BST_DelData(root_node->rchild_p,data);//递归遍历
else //当找到要删除的数值与根节点的数值相等
{
if(root_node->lchild_p != NULL)
//如果左子树存在(如果将此处和下面的'右子树存在'的判断条件替换顺寻则会优先将右子树最小值替换为根节点)
{
node_p max = root_node->lchild_p;
for(;max->rchild_p != NULL;max = max->rchild_p); //查找左子树中的最大值
root_node->data = max->data; //将该子树的最大值复制给根节点
root_node->lchild_p = BST_DelData(root_node->lchild_p,max->data);
//递归删除该子树的最大值
}
else if(root_node->rchild_p != NULL) //如果左子树不存在,而右子树存在
{
node_p min = root_node->rchild_p;
for(;min->lchild_p != NULL;min = min->lchild_p); //查找左子树中的最小值
root_node->data = min->data; //将该子树的最小值复制给根节点
root_node->rchild_p = BST_DelData(root_node->rchild_p,min->data);
//递归删除该子树的最小值
}
else //如果既无左子树也无右子树,即叶子节点,删除该节点
{
free(root_node);
return NULL;
}
}
return root_node;
}更改节点
先删除节点再插入节点即可
不能直接查找到节点后改变节点数值,因为要插入数据不一定就在该二叉树的这个位置,如果强行查找到节点后更改数值,二叉树的结构可能发生改变。
c
node_p BST_ChangeData(node_p root_node,int deldata,int insertdata)
{
if(root_node == NULL)
return NULL;
root_node = BST_DelData(root_node,deldata);
root_node = BST_InsertData(root_node,insertdata);
return root_node;
}销毁二叉树
c
node_p BST_Destroy(node_p root_node)
{
if(root_node == NULL)
return NULL;
if(root_node->lchild_p != NULL)
{
root_node->lchild_p = BST_Destroy(root_node->lchild_p);
}
if(root_node->rchild_p != NULL)
{
root_node->rchild_p = BST_Destroy(root_node->rchild_p);
}
free(root_node);
return NULL;
}八、通用型容器
通用性容器"通常指的是一种可以存储多种不同类型数据的数据结构,但其核心特性是"类型安全"和"代码复用。
在c语言中我们使用结构体和宏函数对数据进行特定操作可以增加代码的复用性。
c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 一、结构体类型(通用型数据通常以结构体存在)
// 日期结构体
typedef struct
{
int year;
int month;
int day;
int hour;
int minute;
} DateTime;
// 1、学生结构体
typedef struct student
{
int id; // 学号
char name[20]; // 姓名
char gender; // 性别(M:男, F:女)
int age; // 年龄
float score; // 分数
char phone[20]; // 电话
float height; // 身高
float weight; // 体重
char class[20]; // 班级
}stu_t, *stu_p;
// 2、航班结构体
typedef struct flight
{
char id[10]; // 航班号(如 "CA123")
char from[50]; // 出发地
char to[50]; // 目的地
int depTime; // 起飞时间(格式 1430 = 14:30)
int arrTime; // 到达时间
int seats; // 总座位数
int booked; // 已预订数
}fly_t, *fly_p;
// 3、医疗挂号结构体
typedef struct medReg
{
int id; // 挂号单号
char name[50]; // 患者姓名
int age; // 年龄
char gender; // 性别(M/F/O)
char dept[30]; // 科室(如 "内科")
char doctor[30]; // 医生姓名
DateTime time; // 挂号时间
float fee; // 费用
int isPaid; // 是否支付(0/1)
} med_t, *med_p;
// 二、为了方便我们进行选择哪个数据类型,而且要通用操作
#define STU_DATA 0
#define FLY_DATA 1
#define MED_DATA 0
#if STU_DATA
#define DATATYPE stu_t
#define DATATYPE_P stu_p
#elif FLY_DATA
#define DATATYPE fly_t
#define DATATYPE_P fly_p
#elif MED_DATA
#define DATATYPE med_t
#define DATATYPE_P med_p
#endif
// 三、为了规范数据类型的作用域,所以需要使用到typedef
typedef DATATYPE datatype;
typedef DATATYPE_P datatype_p;
// 主函数
int main(int argc, char const *argv[])
{
// 进行通用型的设置
datatype_p d_p = malloc(sizeof(datatype));
datatype d = {0};
// 输入数据时是不一样的(用户自己操作)
#if STU_DATA
d.id = 110;
d.score = 100;
#elif FLY_DATA
d.arrTime = 1430;
d.depTime = 1030;
#elif MED_DATA
d.age = 30;
strcpy(d.doctor, "dr.fang");
#endif
*d_p = d; // 相当于你将数据输入后,赋值到一个数据节点中
// 输出数据时是不一样的(用户自己操作)
#if STU_DATA
printf("d.id == %d\n", d.id);
printf("d.score == %f\n", d.score);
#elif FLY_DATA
printf("d.arrTime == %d\n", d.arrTime);
printf("d.depTime == %d\n", d.depTime);
#elif MED_DATA
printf("d.age == %d\n", d.age);
printf("d.doctor == %s\n", d.doctor);
#endif
return 0;
}总结
本篇大致介绍了基础的数据结构。
对顺序表,链式表,以及栈,队列,二叉树等进行了简单介绍。
尽管我已尽力确保内容的准确性,但疏漏仍在所难免。如果您在阅读过程中发现任何错误------无论是错别字、数据错误还是逻辑漏洞------都恳请您在评论区毫不客气地指出。您的每一次指正,都是在帮助我和其他读者获得更准确的知识。先行致谢!