机器学习之逻辑回归

逻辑回归虽然名字中有"回归"，但实际上是一种用于二分类 的经典算法。其核心思想是：对输入特征 x ，建模其属于正类（）的条件概率。该概率通过 Sigmoid 函数将线性组合映射到区间，并假设标签服从伯努利分布。在具体了解其之前，我们先了解几个定义。

名词解释

伯努利分布

伯努利分布又叫0--1分布，假设标签y只可能有以下两种情况：

成功（），概率为
失败（），概率为

其中，就是逻辑回归的概率生成假设。

在对于二分类问题建模时，对于输入的特征，标签y ∈ {0, 1}。伯努利分布的概率质量函数为：, 只要能建模出,那么我们也就完成了概率预测。

sigmoid函数

之前我们学习过线性回归函数，其形式为：，这时候想用线性回归来表示,即希望。这时候我们发现，二者的值域不匹配。因此我们需要想办法把二者的范围处理成一致。

这时候我们引入Sigmoid函数，其形式为：

它可以把任意的实数z映射到(0, 1)之间，且，刚好可以解决概率问题。这时候定义

加入伯努利分布：

这就是逻辑回归的概率模型。

几率

假设一件事件发生的概率为，那么不发生的概率就是，二者的比值就叫一个事件的几率，记为, 该事件的对数几率为。我们发现：

对数几率是输入特征的线性函数。这也是为什么明明是分类却叫"回归"，是因为我们其实就是在对事件的对数几率做线性回归。

逻辑回归

从以上可以得到，逻辑回归其实就是用线性模型去预测某事件的对数几率，通过sigmoid函数转为概率，最后用伯努利分布描述其标签的生成过程，其本质就是对条件概率建模。

在给定输入的特征下，类别为1的条件概率为：;

类别为0的条件概率为：。我们统一写为：

为了推出合理的和，我们使用似然函数求解。

似然

假设你在便利店看到一个人买了一瓶水并马上打开喝了起来，你应该想：他是不是很渴？

概率：他很渴，那么他买水的概率就很高。渴相当于参数，买水就是一个数据结果。概率就是已知参数去预测数据结果出现的可能性。
似然：你看到他买水，反过来推测这个人渴的可能性有多大。跟概率相反，其实就是已经知道了数据结果，去推测参数的合理性。

在上面的式子中，似然函数其实就是关于和的函数，假设我们数据集一共有个样本其中。那么整个数据集的似然函数就是：

我们发现里面是连乘，因此为了计算简便，将上述式子取对数，得到对数似然：

由于我们是要选择使观测数据最可能出现的参数值，也就是做极大似然估计，最大化这个对数似然。但是在机器学习中，我们都是习惯性的最小化损失函数，这时候对其加负号转化为：

上述式子也叫 二分类交叉熵损失函数。

参数更新

有了上述的损失函数，接下来我们只要最小化这个损失函数就好。在这里使用梯度下降法，寻找最优的和。

在求导时，我们先了解sigmoid函数的导数公式：

目标函数

其中

链式求导

对

参数更新

假设学习率为，则参数更新为：

Python代码

使用sklearn中的逻辑回归，首先导入必要的库。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification

使用make_classification创建二分类数据集，含100个样本，每个样本有两个特征（利于画图），并使用LR进行训练。

python 复制代码

# 创建模拟数据集
x_data, y_data = make_classification(
        n_samples=100, 
        n_features=2, 
        n_redundant=0, 
        n_informative=2, 
        n_clusters_per_class=1
        )


# 训练逻辑回归模型
lr = LogisticRegression()
lr.fit(x_data, y_data)

画图

python 复制代码

plt.figure(figsize=(8, 6))
# 绘制数据点：不同类别用不同颜色表示
plt.scatter(
      x_data[:, 0], x_data[:, 1], 
      c=y_data, cmap='RdYlBu', edgecolor='k'
      )
 # x轴范围
x_min, x_max = x_data[:, 0].min() - .5, x_data[:, 0].max() + .5
# y轴范围
y_min, y_max = x_data[:, 1].min() - .5, x_data[:, 1].max() + .5
xx, yy = np.meshgrid(
  np.arange(x_min, x_max, 0.02),  
  np.arange(y_min, y_max, 0.02)
  )
# 预测每个网格点的分类
z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
plt.contour(xx, yy, z, alpha=1, levels=[0.5], colors='black')
plt.xlabel('特征 1')  # x轴标签
plt.ylabel('特征 2')  # y轴标签
# 显示图形
plt.title('含决策边界的逻辑回归')
plt.show()

结果如下

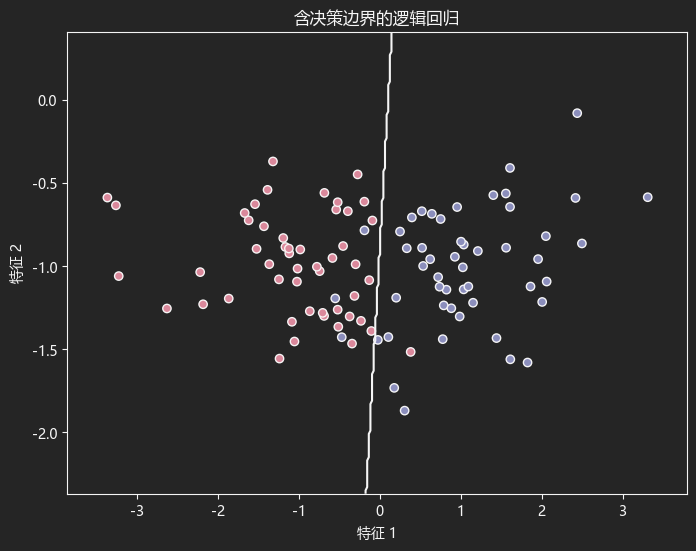
LogisticRegression()

常用参数

penalty: 默认'l2', 表示正则化类型；
fit_intercept: 默认True，是否包含偏置项；
solver: 优化算法，默认'lbfgs'，还有'liblinear', 'sag'等；
max_iter: 最大迭代次数，默认100；
class_weight: 类别的权重，当类别不平衡时可以调整此参数。

主要属性

coef_: 每个特征的系数；
intercept_: 截距；
classes_: 类别标签

常用方法

.fit(train_x, train_y): 模型训练；
.predict(x): 对数据x进行预测；
.predict_proba(x): 每个类别的预测概率；
.score(x, y): 准确率

说明：文中画图代码参考AI。