文章目录
- [1. 模型](#1. 模型)
-
- [1.1 似然函数(Likelihood Function)](#1.1 似然函数(Likelihood Function))
-
- [1.1.1 最大似然估计(maximum likelihood estimation, MLE)](#1.1.1 最大似然估计(maximum likelihood estimation, MLE))
- [2. 分类方法](#2. 分类方法)
-
- [2.1 生成式模型------贝叶斯分类器(Bayes Classifier)](#2.1 生成式模型——贝叶斯分类器(Bayes Classifier))
- [2.2 朴素贝叶斯(Naive Bayes)](#2.2 朴素贝叶斯(Naive Bayes))
- [2.3 贝叶斯网络(Bayesian Networks)](#2.3 贝叶斯网络(Bayesian Networks))
- [2.4 朴素贝叶斯:学习](#2.4 朴素贝叶斯:学习)
- [2.5 MLE问题:数据稀疏性](#2.5 MLE问题:数据稀疏性)
- [2.6 贝叶斯参数估计](#2.6 贝叶斯参数估计)
-
- [2.6.1 贝塔分布(Beta distribution)](#2.6.1 贝塔分布(Beta distribution))
- [2.6.2 最大后验概率估计(Maximum A-Posteriori,MAP)](#2.6.2 最大后验概率估计(Maximum A-Posteriori,MAP))
1. 模型
我们知道机器学习由模型(model)、损失函数(loss function)、优化器(optimizer)和正则化器(regularizer)组成,我们这章将专注于模型和损失函数。
假设我们抛一枚硬币 N = 100 N=100 N=100次,得到的结果是 { x 1 , . . . , x N } \{x_1,...,x_N\} {x1,...,xN},其中 x i ∈ { 0 , 1 } x_i∈\{0,1\} xi∈{0,1},并且 x i = 1 x_i=1 xi=1表示正面(heads,记为 H)。
在这100次抛硬币中,我们得到了 N H = 55 N_H=55 NH=55次正面和 N T = 45 N_T=45 NT=45次反面(tails)。
如果我们再抛一次硬币,它出现正面的概率是多少?让我们为此场景设计一个模型,并拟合这个模型。然后,我们可以使用这个拟合好的模型来预测下一次抛硬币的结果。
假设硬币可能是有偏的(即不是完全公平的)。因此,我们可以假设单次抛硬币的结果 x x x是一个伯努利(Bernoulli)随机变量,其中 x x x可以取两个值:0(反面)或1(正面)。
参数 θ θ θ是未知的,表示硬币正面朝上的概率,其取值范围在 [ 0 , 1 ] [0, 1] [0,1]之间。
p ( x = 1 ∣ θ ) = θ p(x=1∣θ)=θ p(x=1∣θ)=θ表示在给定参数 θ θ θ的条件下,硬币正面朝上的概率。
p ( x = 0 ∣ θ ) = 1 − θ p(x=0∣θ)=1−θ p(x=0∣θ)=1−θ表示在给定参数 θ θ θ的条件下,硬币反面朝上的概率。
这两个概率可以更简洁地表示为 p ( x ∣ θ ) = θ x ( 1 − θ ) 1 − x p(x∣θ)=θ^x(1−θ)^{1−x} p(x∣θ)=θx(1−θ)1−x ,其中 x x x可以是0或1。
假设 { x 1 , . . . , x N } \{x_1,...,x_N\} {x1,...,xN}是独立同分布的(i.i.d.)伯努利随机变量。这意味着每次抛硬币的结果都是独立的,且每次抛掷的硬币都有相同的分布。
给定参数 θ θ θ,所有 N N N次抛硬币结果的联合概率可以表示为:
p ( x 1 , ... , x N ∣ θ ) = ∏ i = 1 N θ x i ( 1 − θ ) 1 − x i p(x_1, \dots, x_N|\theta) = \prod_{i=1}^{N} \theta^{x_i} (1 - \theta)^{1-x_i} p(x1,...,xN∣θ)=∏i=1Nθxi(1−θ)1−xi
这里, ∏ ∏ ∏表示乘积, x i x_i xi是第 i i i次抛掷的结果(0 或 1), θ θ θ是硬币正面朝上的概率。
这个公式表示所有 N N N次抛硬币结果的联合概率是每次抛掷结果概率的乘积。
1.1 似然函数(Likelihood Function)
似然函数是观察到的数据的概率质量(对于离散数据)或概率密度(对于连续数据)作为参数 θ θ θ的函数。
对于硬币抛掷的例子,似然函数 L ( θ ) L(θ) L(θ)表示在给定参数 θ θ θ的情况下,观察到特定数据序列 { x 1 , . . . , x N } \{x_1,...,x_N\} {x1,...,xN}的概率。
公式表示为: L ( θ ) = ∏ i = 1 N θ x i ( 1 − θ ) 1 − x i L(θ) = \prod_{i=1}^{N} \theta^{x_i} (1 - \theta)^{1-x_i} L(θ)=∏i=1Nθxi(1−θ)1−xi
由于直接计算似然函数的乘积可能会遇到数值下溢的问题(特别是当 N 很大时),我们通常使用对数似然函数(Log-likelihood Function),它将乘积转换为求和,从而避免这个问题。
对数似然函数 ℓ ( θ ) ℓ(θ) ℓ(θ)表示为: ℓ ( θ ) = ∑ i = 1 N x i log θ + ( 1 − x i ) log ( 1 − θ ) \ell(\theta) = \sum_{i=1}^{N} x_i \log \theta + (1 - x_i) \log (1 - \theta) ℓ(θ)=∑i=1Nxilogθ+(1−xi)log(1−θ)。
为了选择一个好的 θ θ θ值,我们需要选择一个能够给观察到的数据分配高概率的 θ 值。这被称为最大似然准则。
我们选择使对数似然函数 ℓ ( θ ) ℓ(θ) ℓ(θ)最大化的 θ θ θ值: θ ^ M L = max θ ∈ [ 0 , 1 ] ℓ ( θ ) \hat{\theta}{ML} = \max{\theta \in [0,1]} \ell(\theta) θ^ML=maxθ∈[0,1]ℓ(θ)
这里 θ ^ M L \hat{\theta}_{ML} θ^ML是最大似然估计的 θ θ θ值。
前面我们得到了对数似然函数,我们现在想要到最大值。所以我们现在对对数似然函数 ℓ ( θ ) ℓ(θ) ℓ(θ)求导数。
d ℓ d θ = d d θ ( ∑ i = 1 N x i log θ + ( 1 − x i ) log ( 1 − θ ) ) \frac{d\ell}{d\theta} = \frac{d}{d\theta} \left( \sum_{i=1}^{N} x_i \log \theta + (1 - x_i) \log (1 - \theta) \right) dθdℓ=dθd(∑i=1Nxilogθ+(1−xi)log(1−θ))
= d d θ ( N H log θ + N T log ( 1 − θ ) ) = \frac{d}{d\theta} (N_H \log \theta + N_T \log (1 - \theta)) =dθd(NHlogθ+NTlog(1−θ))
其中 N H = ∑ i x i N_H = \sum_i x_i NH=∑ixi是正面朝上的总次数, N T = N − ∑ i x i N_T = N - \sum_i x_i NT=N−∑ixi反面朝上的总次数。
可以进一步简化为:
= N H θ − N T 1 − θ = \frac{N_H}{\theta} - \frac{N_T}{1 - \theta} =θNH−1−θNT
为了找到使对数似然函数最大化的 θ θ θ值,我们将导数设置为零(这一步其实不严谨,我们应该这里的函数到底是凸函数还是凹函数从而判断这里是最大值还是最小值。我们可以进行二阶导数,发现这个函数在定义域内总是福德,所以对数似然函数是凹的,因此导数为零的点是全局最大值。): N H θ − N T 1 − θ = 0 \frac{N_H}{\theta} - \frac{N_T}{1 - \theta}=0 θNH−1−θNT=0
解这个方程可以得到 θ θ θ的最大似然估计值: θ ^ M L = N H N H + N T \hat{\theta}_{ML} = \frac{N_H}{N_H + N_T} θ^ML=NH+NTNH
1.1.1 最大似然估计(maximum likelihood estimation, MLE)
最大似然估计是一种统计方法,用于根据观测数据估计模型参数,使得观测数据出现的概率最大。
在硬币抛掷的例子中,我们希望找到参数 θ θ θ的值,使得观察到的数据(正面和反面的数量)的概率最大。
这里在进行最大化似然估计的时候其实是在最小化交叉熵。这是因为对数似然函数 ℓ ( θ ) ℓ(θ) ℓ(θ)可以表示为: ℓ ( θ ) = ∑ i = 1 N x i log θ + ( 1 − x i ) log ( 1 − θ ) \ell(\theta) = \sum_{i=1}^{N} x_i \log \theta + (1 - x_i) \log (1 - \theta) ℓ(θ)=∑i=1Nxilogθ+(1−xi)log(1−θ)
为了找到使 ℓ ( θ ) \ell(\theta) ℓ(θ)最大化的 θ \theta θ值,我们可以等价地最小化其负值 − ℓ ( θ ) -\ell(\theta) −ℓ(θ):
θ ^ M L = min θ ∈ [ 0 , 1 ] − ℓ ( θ ) \hat{\theta}{ML} = \min{\theta \in [0,1]} -\ell(\theta) θ^ML=minθ∈[0,1]−ℓ(θ)
这等价于最小化交叉熵,因为交叉熵可以表示为:
H ( p , q ) = − ∑ i p i log q i H(p, q) = - \sum_i p_i \log q_i H(p,q)=−∑ipilogqi
在我们的例子中, p p p是真实分布(正面和反面的实际概率),而 q q q是模型分布(由参数 θ \theta θ定义的分布)。
2. 分类方法
机器学习中有两种主要的分类方法:
- 判别式方法(Discriminative approach):
判别式方法直接从标记样本中估计决策边界或类别分隔器的参数。
模型:直接建模 p ( t ∣ x ) p(t∣x) p(t∣x),即给定输入 x x x属于类别 t t t的概率(例如逻辑回归模型)。
学习:学习从输入到类别的映射(例如线性/逻辑回归、决策树等)。
目标:解决"如何分离类别"的问题,即如何找到最佳的方式来区分不同的类别。 - 生成式方法(Generative approach):
生成式方法建模输入数据属于某个类别的特征分布(例如贝叶斯分类器)。
模型:建模 p ( x ∣ t ) p(x∣t) p(x∣t),即给定类别 t t t时输入 x x x的概率分布。
应用:应用贝叶斯规则来推导 p ( t ∣ x ) p(t∣x) p(t∣x),即给定输入 x x x属于类别 t t t的概率。
目标:解决"每个类别看起来像什么"的问题,即尝试理解每个类别的输入数据的分布特征。
判别式方法和生成式方法的关键区别在于是否对输入数据有分布假设。生成式方法需要对输入数据的分布做出假设,而判别式方法则不需要。
假设我们有一个简单的二分类问题,比如预测电子邮件是否为垃圾邮件。我们有一组特征,比如邮件中某些关键词的出现频率。
判别式方法(逻辑回归)会直接学习一个模型来预测给定邮件是垃圾邮件的概率。这个模型不考虑邮件内容是如何生成的,它只关心如何根据邮件内容(特征)来区分垃圾邮件和非垃圾邮件。
逻辑回归模型可能会学习到这样的规则:如果邮件中"免费"这个词的出现频率高,那么这封邮件更有可能是垃圾邮件。逻辑回归模型的目标是找到一个决策边界,将邮件分为垃圾邮件和非垃圾邮件两类。'生成式方法(朴素贝叶斯分类器)会尝试理解垃圾邮件和非垃圾邮件的生成过程。它假设邮件中的每个词是独立生成的,并尝试学习每个词在垃圾邮件和非垃圾邮件中出现的概率。
例如,朴素贝叶斯分类器可能会学习到以下概率:
"免费"这个词在垃圾邮件中出现的概率是0.4,在非垃圾邮件中出现的概率是0.01。
"会议"这个词在垃圾邮件中出现的概率是0.02,在非垃圾邮件中出现的概率是0.3。
然后,当收到一封新邮件时,朴素贝叶斯分类器会计算这封邮件是垃圾邮件的概率和非垃圾邮件的概率,然后选择概率更大的那个类别作为预测结果。
判别式方法关注的是"给定输入,哪个类别更可能?"它直接学习输入特征和类别之间的映射关系。
生成式方法关注的是"每个类别的输入特征分布是什么样的?"它试图学习输入特征的生成过程,然后通过贝叶斯定理来预测类别。
如果还不理解可以回头再来看这个例子,下面我们仔细贝叶斯分类器(Bayes Classifier)。
2.1 生成式模型------贝叶斯分类器(Bayes Classifier)
我们现在尝试对文本进行分类从而将电子邮件分为垃圾邮件(spam)和非垃圾邮件(not-spam)。在这个例子中,垃圾邮件用 c = 1 c=1 c=1表示,非垃圾邮件用 c = 0 c=0 c=0表示。
现在我们收到了一句话"You are one of the very few who have been selected as a winners for the free $1000 Gift Card."我们需要判断其是否是垃圾邮件。
在文本处理中,词汇表是指在所有文档中出现的不同单词的集合。
我们可以使用词袋模型从而将文本转换为一个长向量,其中每个维度对应词汇表中的一个单词。
在这个向量中,如果某个单词在文本中出现,则对应的维度值为1;如果没有出现,则为0。
因此对于每封电子邮件,我们创建一个二进制向量 x x x,其中每个元素对应词汇表中的一个单词。
这里"a": 1(表示"a"在邮件中出现)
"car": 0(表示"car"在邮件中没有出现)
"card": 1(表示"card"在邮件中出现)
"win": 0(表示"win"在邮件中没有出现)
"winner": 1(表示"winner"在邮件中出现)
"winter": 0(表示"winter"在邮件中没有出现)
"you": 1(表示"you"在邮件中出现)
现在我们使用贝叶斯定理来计算给定特征向量 x x x的类别概率。
给定特征向量 x = [ x 1 , x 2 , . . . , x D ] T \mathbf{x}=[x_1,x_2,...,x_D]^T x=[x1,x2,...,xD]T,我们想要计算类别概率 p ( c ∣ x ) p(c∣x) p(c∣x),即给定特征向量 x x x属于类别 c c c的概率。
p ( c ∣ x ) = p ( x , c ) p ( x ) = p ( x ∣ c ) p ( c ) p ( x ) p(c|\mathbf{x}) = \frac{p(\mathbf{x}, c)}{p(\mathbf{x})} = \frac{p(\mathbf{x}|c) p(c)}{p(\mathbf{x})} p(c∣x)=p(x)p(x,c)=p(x)p(x∣c)p(c)
p ( x ∣ c ) p(\mathbf{x}|c) p(x∣c):给定类别 c c c时特征向量 x \mathbf{x} x的概率(类条件概率)。
p ( c ) p(c) p(c):类别 c c c的先验概率。
p ( x ) p(\mathbf{x}) p(x):特征向量 x \mathbf{x} x的边缘概率。
更正式的表达为:
后验概率可以表示为: posterior = Class likelihood × prior Evidence \text{posterior} = \frac{\text{Class likelihood} \times \text{prior}}{\text{Evidence}} posterior=EvidenceClass likelihood×prior
其中:
Class likelihood \text{Class likelihood} Class likelihood是类条件概率 p ( x ∣ c ) p(x∣c) p(x∣c)。
prior \text{prior} prior是类别的先验概率 p ( c ) p(c) p(c)。
Evidence \text{Evidence} Evidence是特征向量的边缘概率 p ( x ) p(x) p(x)。
对于二分类问题,我们可以通过以下公式计算 p ( x ) p(x) p(x):
p ( x ) = p ( x ∣ c = 0 ) p ( c = 0 ) + p ( x ∣ c = 1 ) p ( c = 1 ) p(\mathbf{x}) = p(\mathbf{x}|c=0)p(c=0) + p(\mathbf{x}|c=1)p(c=1) p(x)=p(x∣c=0)p(c=0)+p(x∣c=1)p(c=1)
这个公式表示特征向量 x x x的边缘概率是两个类别的类条件概率和先验概率的加权和。
为了计算 p ( c ∣ x ) p(c∣x) p(c∣x),我们需要知道 p ( x ∣ c ) p(x∣c) p(x∣c)和 p ( c ) p(c) p(c)。
2.2 朴素贝叶斯(Naive Bayes)
朴素贝叶斯是一种生成式模型,用于分类问题,特别是文本分类。
假设我们有两个类别:垃圾邮件(spam)和非垃圾邮件(non-spam)。
我们有一个包含 D D D个单词的词典,以及一个二进制特征向量 x = [ x 1 , x 2 , . . . , x D ] \mathbf{x}=[x_1,x_2,...,x_D] x=[x1,x2,...,xD],其中每个 x i x_i xi表示词典中的第 i i i个单词是否出现在邮件中(1 表示出现,0 表示未出现)。
如果我们定义一个联合分布 p ( c , x 1 , ⋯ , x D ) p(c,x_1 ,⋯,x_D) p(c,x1,⋯,xD),这将提供足够的信息来确定 p ( c ) p(c) p(c)和 p ( x ∣ c ) p(x∣c) p(x∣c)。
p ( c ) p(c) p(c)是类别 c c c的先验概率。
p ( x ∣ c ) p(x∣c) p(x∣c)是给定类别 c c c时特征向量 x 的概率。
问题在于,指定一个包含 D + 1 D+1 D+1个二进制变量的联合分布需要 2 D + 1 − 1 2^{D+1}-1 2D+1−1个条目。这在计算上是不可行的,并且需要大量的数据来拟合。
我们希望对分布施加某种结构,使其可以紧凑地表示,并且学习和推理都是可行的。
而朴素贝叶斯分类器通过假设特征之间相互独立来解决这个问题。朴素贝叶斯假设给定类别 c c c后,特征 x i x_i xi是条件独立的。这意味着在已知邮件类别(垃圾邮件或非垃圾邮件)的情况下,邮件中各个单词的出现是相互独立的。
这意味着 x i x_i xi和 x j x_j xj在条件分布 p ( x ∣ c ) p(x∣c) p(x∣c)下是独立的。但请注意,这并不意味着它们在绝对意义上是独立的。
因此我们可以将联合分布分解为条件分布的乘积:
p ( c , x 1 , x 2 , ... , x D ) = p ( c ) p ( x 1 ∣ c ) p ( x 2 ∣ c ) ⋯ p ( x D ∣ c ) p(c, x_1, x_2, \ldots, x_D) = p(c) p(x_1|c) p(x_2|c) \cdots p(x_D|c) p(c,x1,x2,...,xD)=p(c)p(x1∣c)p(x2∣c)⋯p(xD∣c)
这样,我们只需要估计每个特征的条件概率 p ( x i ∣ c ) p(x_i|c) p(xi∣c),而不是整个联合分布。
类别的先验概率: p ( c = 1 ) = π p(c = 1) = \pi p(c=1)=π(例如,垃圾邮件的概率)
给定类别下特征的条件概率: p ( x j = 1 ∣ c ) = θ j c p(x_j = 1 | c) = \theta_{jc} p(xj=1∣c)=θjc(例如,单词"price"在垃圾邮件中出现的概率)
总共需要 2 D + 1 2D + 1 2D+1个参数(在 2 D + 1 − 1 2^{D+1} - 1 2D+1−1之前):
- D D D个特征的条件概率 p ( x j = 1 ∣ c ) p(x_j = 1 | c) p(xj=1∣c)对于每个类别。
- 1 1 1个类别的先验概率 p ( c ) p(c) p(c)。
2.3 贝叶斯网络(Bayesian Networks)
贝叶斯网络是一种概率图模型,用于表示一组随机变量及其条件依赖关系。
贝叶斯网络使用有向图模型来表示模型。在图中,节点表示随机变量,有向边表示变量之间的条件依赖关系。

这种图结构意味着联合分布可以分解为每个变量给定其父节点的条件分布的乘积。这是概率图模型的一个关键特性,它允许我们以更紧凑的形式表示复杂的概率分布。
直观上,你可以将图中的边视为反映因果结构。然而,从数学上讲,这种解释并不总是成立,除非有额外的假设。贝叶斯网络中的边主要表示条件依赖关系,而不是直接的因果关系。
2.4 朴素贝叶斯:学习
这里参数可以高效地学习,因为对数似然函数可以分解为每个特征的独立项。
对数似然函数的初始表达式:
ℓ ( θ ) = ∑ i = 1 N log p ( c ( i ) , x ( i ) ) = ∑ i = 1 N log { p ( x ( i ) ∣ c ( i ) ) p ( c ( i ) ) } \ell(\theta) = \sum_{i=1}^{N} \log p(c^{(i)}, \mathbf{x}^{(i)}) = \sum_{i=1}^{N} \log \left\{ p(\mathbf{x}^{(i)}|c^{(i)}) p(c^{(i)}) \right\} ℓ(θ)=∑i=1Nlogp(c(i),x(i))=∑i=1Nlog{p(x(i)∣c(i))p(c(i))}
进一步分解为条件概率的乘积:
= ∑ i = 1 N log { p ( c ( i ) ) ∏ j = 1 D p ( x j ( i ) ∣ c ( i ) ) } = \sum_{i=1}^{N} \log \left\{ p(c^{(i)}) \prod_{j=1}^{D} p(x_j^{(i)} | c^{(i)}) \right\} =∑i=1Nlog{p(c(i))∏j=1Dp(xj(i)∣c(i))}
分解为类别的先验概率和特征的条件概率的和:
= ∑ i = 1 N [ log p ( c ( i ) ) + ∑ j = 1 D log p ( x j ( i ) ∣ c ( i ) ) ] = \sum_{i=1}^{N} \left[ \log p(c^{(i)}) + \sum_{j=1}^{D} \log p(x_j^{(i)} | c^{(i)}) \right] =∑i=1N[logp(c(i))+∑j=1Dlogp(xj(i)∣c(i))]
最终分解为类别的伯努利对数似然和每个特征的伯努利对数似然的和:
= ∑ i = 1 N log p ( c ( i ) ) ⏟ Bernoulli log-likelihood of labels + ∑ j = 1 D ∑ i = 1 N log p ( x j ( i ) ∣ c ( i ) ) ⏟ Bernoulli log-likelihood for feature x j = \underbrace{\sum_{i=1}^{N} \log p(c^{(i)})}{\text{Bernoulli log-likelihood of labels}} + \sum{j=1}^{D} \underbrace{\sum_{i=1}^{N} \log p(x_j^{(i)} | c^{(i)})}_{\text{Bernoulli log-likelihood for feature } x_j} =Bernoulli log-likelihood of labels i=1∑Nlogp(c(i))+∑j=1DBernoulli log-likelihood for feature xj i=1∑Nlogp(xj(i)∣c(i))
由于对数似然函数可以分解为独立的项,我们可以分别优化每个特征的条件概率参数 p ( x j = 1 ∣ c ) p(x_j =1∣c) p(xj=1∣c)和类别的先验概率 p ( c ) p(c) p(c)。
我们现在先最大化先验概率的对数似然函数:
∑ i = 1 N log p ( c ( i ) ) \sum_{i=1}^{N} \log p(c^{(i)}) ∑i=1Nlogp(c(i))
这是我们之前硬币投掷示例的一个变体。设 p ( c ( i ) = 1 ) = π p(c^{(i)}=1)=\pi p(c(i)=1)=π。注意 p ( c ( i ) ) = π c ( i ) ( 1 − π ) 1 − c ( i ) p(c^{(i)}) = \pi^{c^{(i)}} (1 - \pi)^{1-c^{(i)}} p(c(i))=πc(i)(1−π)1−c(i)
对数似然函数的展开:
∑ i = 1 N log p ( c ( i ) ) = ∑ i = 1 N c ( i ) log π + ∑ i = 1 N ( 1 − c ( i ) ) log ( 1 − π ) \sum_{i=1}^{N} \log p(c^{(i)}) = \sum_{i=1}^{N} c^{(i)} \log \pi + \sum_{i=1}^{N} (1 - c^{(i)}) \log (1 - \pi) ∑i=1Nlogp(c(i))=∑i=1Nc(i)logπ+∑i=1N(1−c(i))log(1−π)
通过将导数设为零来获得最大似然估计(MLEs):
π ^ = ∑ i I [ c ( i ) = 1 ] N = # spams in dataset total # samples \hat{\pi} = \frac{\sum_{i} \mathbb{I}[c^{(i)} = 1]}{N} = \frac{\# \text{ spams in dataset}}{\text{total \# samples}} π^=N∑iI[c(i)=1]=total # samples# spams in dataset
其中 I [ c ( i ) = 1 ] \mathbb{I}[c^{(i)} = 1] I[c(i)=1]是指示函数,当 c ( i ) = 1 c^{(i)} = 1 c(i)=1时为 1,否则为 0。
我们现在最大化每个特征的条件概率: ∑ i = 1 N log p ( x j ( i ) ∣ c ( i ) ) \sum_{i=1}^{N} \log p(x_j^{(i)} | c^{(i)}) ∑i=1Nlogp(xj(i)∣c(i))
再次提醒一下,这是我们之前硬币投掷示例的一个变体。 θ j c = p ( x j ( i ) = 1 ∣ c ) \theta_{jc} = p(x_j^{(i)} = 1 | c) θjc=p(xj(i)=1∣c), p ( x j ( i ) ∣ c ) = θ j c x j ( i ) ( 1 − θ j c ) 1 − x j ( i ) p(x_j^{(i)} | c) = \theta_{jc}^{x_j^{(i)}} (1 - \theta_{jc})^{1 - x_j^{(i)}} p(xj(i)∣c)=θjcxj(i)(1−θjc)1−xj(i)
对数似然函数可以表示为: ∑ i = 1 N log p ( x j ( i ) ∣ c ( i ) ) = ∑ i = 1 N c ( i ) { x j ( i ) log θ j 1 + ( 1 − x j ( i ) ) log ( 1 − θ j 1 ) } + ∑ i = 1 N ( 1 − c ( i ) ) { x j ( i ) log θ j 0 + ( 1 − x j ( i ) ) log ( 1 − θ j 0 ) } \sum_{i=1}^{N} \log p(x_j^{(i)} | c^{(i)}) = \sum_{i=1}^{N} c^{(i)} \left\{ x_j^{(i)} \log \theta_{j1} + (1 - x_j^{(i)}) \log (1 - \theta_{j1}) \right\} + \sum_{i=1}^{N} (1 - c^{(i)}) \left\{ x_j^{(i)} \log \theta_{j0} + (1 - x_j^{(i)}) \log (1 - \theta_{j0}) \right\} ∑i=1Nlogp(xj(i)∣c(i))=∑i=1Nc(i){xj(i)logθj1+(1−xj(i))log(1−θj1)}+∑i=1N(1−c(i)){xj(i)logθj0+(1−xj(i))log(1−θj0)}
为了找到 θ j c θ_{jc} θjc的最大似然估计,我们将导数设为零: θ ^ j c = ∑ i I [ x j ( i ) = 1 and c ( i ) = c ] ∑ i I [ c ( i ) = c ] \hat{\theta}{jc} = \frac{\sum{i} \mathbb{I}[x_j^{(i)} = 1 \text{ and } c^{(i)} = c]}{\sum_{i} \mathbb{I}[c^{(i)} = c]} θ^jc=∑iI[c(i)=c]∑iI[xj(i)=1 and c(i)=c]
对于 c = 1 c = 1 c=1(垃圾邮件),这可以简化为:
θ ^ j 1 = # word j appears in spams # spams in dataset \hat{\theta}_{j1} = \frac{\text{\# word } j \text{ appears in spams}}{\text{\# spams in dataset}} θ^j1=# spams in dataset# word j appears in spams
我们现在讲解如何使用贝叶斯规则来预测新数据点的类别。
我们使用贝叶斯规则计算后验概率:
p ( c ∣ x ) = p ( c ) p ( x ∣ c ) ∑ c ′ p ( c ′ ) p ( x ∣ c ′ ) p(c|\mathbf{x}) = \frac{p(c)p(\mathbf{x}|c)}{\sum_{c'} p(c')p(\mathbf{x}|c')} p(c∣x)=∑c′p(c′)p(x∣c′)p(c)p(x∣c)
其中, p ( c ) p(c) p(c)是类别 c c c的先验概率, p ( x ∣ c ) p(\mathbf{x}|c) p(x∣c)是给定类别 c c c时特征向量 x \mathbf{x} x的概率。
由于朴素贝叶斯假设特征之间条件独立,我们可以将 p ( x ∣ c ) p(\mathbf{x}|c) p(x∣c)表示为:
p ( x ∣ c ) = ∏ j = 1 D p ( x j ∣ c ) p(\mathbf{x} | c) = \prod_{j=1}^{D} p(x_j | c) p(x∣c)=∏j=1Dp(xj∣c)
因此,后验概率可以写为:
p ( c ∣ x ) = p ( c ) ∏ j = 1 D p ( x j ∣ c ) ∑ c ′ p ( c ′ ) ∏ j = 1 D p ( x j ∣ c ′ ) p(c|\mathbf{x}) = \frac{p(c) \prod_{j=1}^{D} p(x_j|c)}{\sum_{c'} p(c') \prod_{j=1}^{D} p(x_j|c')} p(c∣x)=∑c′p(c′)∏j=1Dp(xj∣c′)p(c)∏j=1Dp(xj∣c)
如果我们只是想确定最可能的类别 c,我们不需要计算分母。这是因为分母对于所有类别 c 是相同的,因此在比较不同类别的后验概率时可以忽略。
使用简写符号表示后验概率:
p ( c ∣ x ) ∝ p ( c ) ∏ j = 1 D p ( x j ∣ c ) p(c|\mathbf{x}) \propto p(c) \prod_{j=1}^{D} p(x_j|c) p(c∣x)∝p(c)∏j=1Dp(xj∣c)
对于输入 x \mathbf{x} x,通过比较不同类别 c c c的 c = arg max c p ( c ) ∏ j = 1 D p ( x j ∣ c ) c = \arg\max_c p(c) \prod_{j=1}^{D} p(x_j|c) c=argmaxcp(c)∏j=1Dp(xj∣c)的值来进行预测(例如,选择最大的值)。
小结一下:
朴素贝叶斯是一种非常经济的学习算法。
在训练阶段,朴素贝叶斯通过最大似然估计来估计模型参数。
具体来说,它计算每个特征与标签的共同出现次数。这个过程只需要对数据集进行一次遍历(单次扫描)。
在测试阶段,朴素贝叶斯应用贝叶斯规则来进行分类。
由于模型结构简单,测试阶段的计算成本也很低。然而,对于更复杂的模型,贝叶斯推理可能会非常昂贵和/或复杂。
虽然这里讨论的是伯努利(二元特征)情况以简化说明,但朴素贝叶斯的分析可以很容易地扩展到其他类型的概率分布。
由于朴素贝叶斯假设特征之间相互独立(即"朴素"的独立性假设),这在实际应用中通常不如判别式模型准确。
这里推荐观看下列视频,这个视频博主介绍的比较清楚,能让你对朴素贝叶斯有个基础的认识。朴素贝叶斯讲解
2.5 MLE问题:数据稀疏性
最大似然估计(MLE)的一个主要缺点是,如果数据量太少,模型可能会过拟合(overfit)。
例如抛硬币两次,每次都得到正面(H)。在这种情况下,最大似然估计会计算正面的概率:
θ M L = N H N H + N T = 2 2 + 0 = 1 \theta_{ML} = \frac{N_H}{N_H + N_T} = \frac{2}{2 + 0} = 1 θML=NH+NTNH=2+02=1
由于在示例中从未观察到反面(T),MLE将反面的概率分配为0。这种情况被称为数据稀疏性问题,因为它导致模型对未观察到的事件的概率估计为0,这在实际应用中通常是不合理的。
解决方法:
- 平滑技术:为了解决数据稀疏性问题,常用的方法是应用平滑技术,如拉普拉斯平滑(Laplace smoothing)或加法平滑(additive smoothing),这些技术通过在计数中添加一个小的常数来避免概率为0的情况。
- 正则化:另一种方法是使用正则化技术,如L1或L2正则化,这些技术可以帮助控制模型的复杂度,减少过拟合的风险。
2.6 贝叶斯参数估计
在最大似然估计中,观测数据被视为随机变量,而参数(如 θ)被视为固定的未知常数,目标是找到使观测数据概率最大的参数值。
贝叶斯方法则将参数也视为随机变量。这意味着在贝叶斯框架下,参数本身具有概率分布,其不确定性可以通过先验分布来表达。
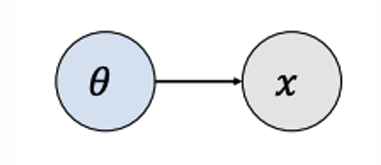
在MLE中,参数 θ θ θ直接影响观测数据 x x x。
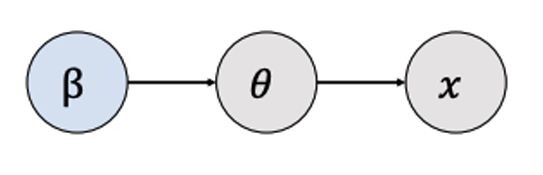
在贝叶斯方法中,参数 θ θ θ不仅影响观测数据 x x x,而且其自身也受到另一个参数集 β β β的影响, β β β定义了 θ θ θ的先验分布。
要定义一个贝叶斯模型,需要指定两个分布:
先验分布 p ( θ ) p(θ) p(θ):这表示在观察数据之前,我们对参数 θ θ θ的信念或先验知识。先验分布反映了参数的不确定性和我们对参数可能取值的预期。
似然函数 p ( D ∣ θ ) p(D∣θ) p(D∣θ):这与最大似然估计中的似然函数相同,表示给定参数 θ θ θ时观测数据 D D D的概率。
当我们根据观测数据更新我们的观点时,我们使用贝叶斯规则来计算后验分布 p ( θ ∣ D ) p(θ∣D) p(θ∣D)。
p ( θ ∣ D ) = p ( θ ) p ( D ∣ θ ) ∫ p ( θ ′ ) p ( D ∣ θ ′ ) d θ ′ p(\theta | \mathcal{D}) = \frac{p(\theta) p(\mathcal{D} | \theta)}{\int p(\theta') p(\mathcal{D} | \theta') \, \mathrm{d}\theta'} p(θ∣D)=∫p(θ′)p(D∣θ′)dθ′p(θ)p(D∣θ)
其中:
p ( θ ) p(θ) p(θ)是参数 θ θ θ的先验分布,表示在观察数据之前我们对参数的信念。
p ( D ∣ θ ) p(D∣θ) p(D∣θ)是似然函数,表示给定参数 θ θ θ时观测数据 D D D的概率。
分母是边缘似然或证据,它是一个归一化常数,确保后验分布的总概率为1。
我们很少显式地计算分母(即边缘似然),因为它通常在计算上是不可行的。这个积分可能涉及到高维空间,使得直接计算变得非常复杂或不可能。
我们再回到硬币抛掷问题上。
硬币抛掷问题的似然函数:
L ( θ ) = p ( D ∣ θ ) = θ N H ( 1 − θ ) N T L(\theta) = p(\mathcal{D}|\theta) = \theta^{N_H}(1 - \theta)^{N_T} L(θ)=p(D∣θ)=θNH(1−θ)NT
在贝叶斯方法中,我们需要为参数 θ θ θ指定一个先验分布。先验分布反映了我们在观察数据之前对参数的先验信念。
可以选择一个非信息性先验(uninformative prior),它尽可能少地假设信息。一个合理的选择是均匀先验。
然而,根据经验,我们知道某些值(如0.5)比极端值(如0.99)更有可能。因此,一个特别有用的先验分布是贝塔分布(beta distribution):
p ( θ ; a , b ) = Γ ( a + b ) Γ ( a ) Γ ( b ) θ a − 1 ( 1 − θ ) b − 1 p(\theta; a, b) = \frac{\Gamma(a + b)}{\Gamma(a)\Gamma(b)} \theta^{a-1}(1 - \theta)^{b-1} p(θ;a,b)=Γ(a)Γ(b)Γ(a+b)θa−1(1−θ)b−1
其中 Γ \Gamma Γ是伽马函数, a a a和 b b b是贝塔分布的参数。
为了简化表示,可以使用比例符号来忽略归一化常数:
p ( θ ; a , b ) ∝ θ a − 1 ( 1 − θ ) b − 1 p(\theta; a, b) \propto \theta^{a-1}(1 - \theta)^{b-1} p(θ;a,b)∝θa−1(1−θ)b−1
2.6.1 贝塔分布(Beta distribution)
贝塔分布是一种连续概率分布,常用于表示概率或比例的先验分布。
下图展示了不同参数 a a a和 b b b值下的贝塔分布曲线。

贝塔分布的期望值 E [ θ ] = a a + b \mathbb{E}[\theta] = \frac{a}{a + b} E[θ]=a+ba
当 a a a和 b b b的值较大时,分布会变得更尖锐,即更集中在期望值附近。
当 a = b = 1 a=b=1 a=b=1时,贝塔分布退化为均匀分布,这是贝塔分布的一个特例。
贝塔分布常被用作伯努利分布(Bernoulli distribution)的先验分布,因为伯努利分布描述的是只有两个可能结果(如硬币的正面或反面)的随机变量,而贝塔分布自然适合描述这类二元结果的概率。
这里顺便正式介绍一下伯努利分布(Bernoulli distribution),就像我们前文示例的那样。
伯努利随机变量 X X X取值为1(成功)的概率是 p p p,取值为 0(失败)的概率是 1 − p 1−p 1−p。
伯努利分布的概率质量函数(probability mass function, PMF)是:
P ( X = k ) = p k ( 1 − p ) 1 − k P(X=k)=p^k(1-p)^{1-k} P(X=k)=pk(1−p)1−k其中 k ∈ 0 , 1 k∈{0,1} k∈0,1
伯努利分布的期望值(均值)是 p p p,方差是 p ( 1 − p ) p(1−p) p(1−p)。
后验分布 p ( θ ∣ D ) p(θ∣D) p(θ∣D)与先验分布 p ( θ ) p(θ) p(θ)和似然函数 p ( D ∣ θ ) p(D∣θ) p(D∣θ)成正比:
p ( θ ∣ D ) ∝ p ( θ ) p ( D ∣ θ ) p(\theta | \mathcal{D}) \propto p(\theta) p(\mathcal{D} | \theta) p(θ∣D)∝p(θ)p(D∣θ)
具体来说,如果先验分布是贝塔分布,似然函数是伯努利分布,那么后验分布也是贝塔分布:
∝ [ θ a − 1 ( 1 − θ ) b − 1 ] [ θ N H ( 1 − θ ) N T ] \propto \left[ \theta^{a-1} (1 - \theta)^{b-1} \right] \left[ \theta^{N_H} (1 - \theta)^{N_T} \right] ∝[θa−1(1−θ)b−1][θNH(1−θ)NT]
= θ a − 1 + N H ( 1 − θ ) b − 1 + N T = \theta^{a-1+N_H} (1 - \theta)^{b-1+N_T} =θa−1+NH(1−θ)b−1+NT
后验分布是贝塔分布,其参数为 N H + a N_H + a NH+a和 N T + b N_T + b NT+b。
后验期望的 θ \theta θ是:
E [ θ ∣ D ] = N H + a N H + N T + a + b \mathbb{E}[\theta | \mathcal{D}] = \frac{N_H + a}{N_H + N_T + a + b} E[θ∣D]=NH+NT+a+bNH+a
先验分布的参数 a 和 b 可以被视为"伪计数"(pseudo-counts)。
这是因为先验分布和似然函数具有相同的函数形式,这种现象称为共轭性(conjugacy),共轭先验非常有用。
这里解释一下共轭性:
如果一个分布族是另一个分布族的共轭先验,那么:
先验分布:属于这个特定的分布族,它描述了在观察数据之前我们对参数的先验知识或信念。
似然函数:通常与数据生成过程有关,描述了给定参数值时观测数据的概率。
后验分布:在观测了数据之后,根据贝叶斯定理,后验分布仍然属于先验分布的那个分布族,但参数会根据观测数据进行更新。
共轭性的优点在于:
计算简便:由于后验分布的形式已知,许多计算(如后验均值、方差等)可以直接应用该分布的公式得到,而不需要进行复杂的积分运算。
解析解:在某些情况下,共轭先验可以提供解析解,这在数值方法难以应用或计算量很大时特别有用。
直观性:共轭先验使得参数的更新过程更加直观,因为后验分布的形式与先验分布相似,只是参数发生了变化。
下图展示了先验分布、似然函数和后验分布之间的关系。
下图展示了在小数据设置下( N H = 2 , N T = 0 N_H=2,N_T =0 NH=2,NT=0)的贝叶斯推断。

在这种情况下,先验分布(蓝色曲线)对后验分布(红色曲线)有较大的影响,因为观测数据较少,不足以强烈影响我们对参数的信念。
后验分布的形状更接近先验分布,但略微向似然函数(绿色曲线)的峰值移动。
下图展示了在大数据设置下( N H = 55 , N T = 45 N_H=55,N_T =45 NH=55,NT=45)的贝叶斯推断。
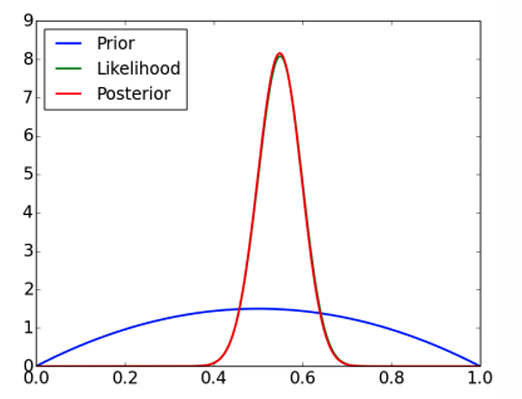
在这种情况下,观测数据量较大,足以压倒先验分布的影响,使得后验分布(红色曲线)主要受似然函数(绿色曲线)的形状影响。
后验分布的形状与似然函数非常接近,表明数据在确定参数估计中起主导作用。
当观测数据量足够大时,数据的影响会超过先验分布的影响,即"数据压倒先验"(data overwhelm the prior)。
这表明在大数据量下,后验分布主要由数据决定,先验分布的影响变得次要。
2.6.2 最大后验概率估计(Maximum A-Posteriori,MAP)
MAP估计是一种在贝叶斯框架下寻找参数最可能值的方法,它考虑了先验分布和似然函数,以确定在给定数据下参数的最可能设置。
MAP估计旨在找到在后验分布下参数的值,该值使得后验概率最大。
下图展示了三种分布。
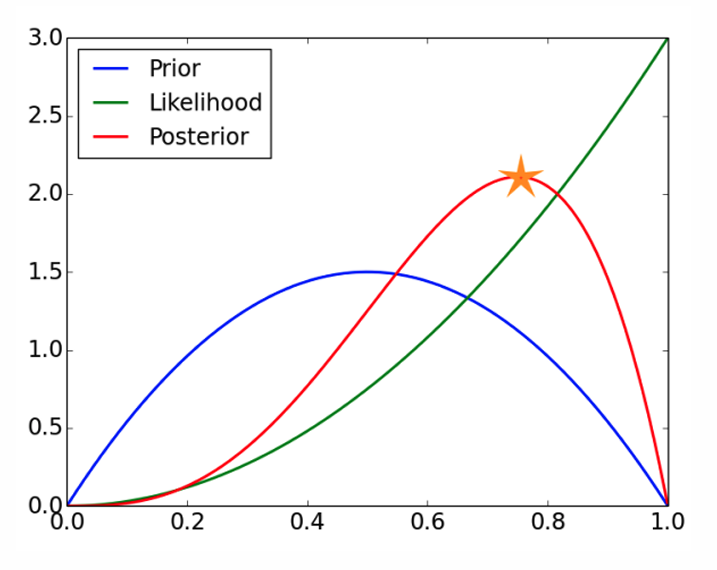
星号标记的位置表示MAP估计的参数值,即后验分布的峰值位置。
下面展示这个优化问题的推导,概括来说:我们不再求整个后验分布,而是只找使后验概率最大的那个参数值 θ ^ MAP \hat{\theta}{\text{MAP}} θ^MAP
θ ^ MAP = arg max θ p ( θ ∣ D ) \hat{\theta}{\text{MAP}} = \arg\max_{\theta} \, p(\theta \mid \mathcal{D}) θ^MAP=argmaxθp(θ∣D)
分母 p ( D ) ) p(\mathcal{D})) p(D))与 θ θ θ无关,可以丢掉。
= arg max θ p ( θ , D ) = \arg\max_{\theta} \, p(\theta, \mathcal{D}) =argmaxθp(θ,D)
联合概率 = 先验 × 似然。
= arg max θ p ( θ ) p ( D ∣ θ ) = \arg\max_{\theta} \, p(\theta)\, p(\mathcal{D} \mid \theta) =argmaxθp(θ)p(D∣θ)
我们取对数,对数不改变极值点,却能把乘积变求和,方便求导、数值稳定。
= arg max θ [ log p ( θ ) + log p ( D ∣ θ ) ] = \arg\max_{\theta} \, \Bigl[ \log p(\theta) + \log p(\mathcal{D} \mid \theta) \Bigr] =argmaxθ[logp(θ)+logp(D∣θ)]
把先验(Beta)与似然(Bernoulli)取对数后相加:
log p ( θ , D ) = log p ( θ ) + log p ( D ∣ θ ) \log p(\theta,\mathcal{D}) =\log p(\theta) + \log p(\mathcal{D} \mid \theta) logp(θ,D)=logp(θ)+logp(D∣θ)
= Const + ( a − 1 ) log θ + ( b − 1 ) log ( 1 − θ ) + N H log θ + N T log ( 1 − θ ) =\text{Const} + (a - 1)\log\theta + (b - 1)\log(1-\theta)+N_H\log\theta+N_T\log(1-\theta) =Const+(a−1)logθ+(b−1)log(1−θ)+NHlogθ+NTlog(1−θ)
= Const + ( N H + a − 1 ) log θ + ( N T + b − 1 ) log ( 1 − θ ) = \text{Const} + (N_H + a - 1)\log\theta + (N_T + b - 1)\log(1-\theta) =Const+(NH+a−1)logθ+(NT+b−1)log(1−θ)
求导并令为零:
d d θ log p ( θ , D ) = N H + a − 1 θ − N T + b − 1 1 − θ = 0 \frac{d}{d\theta}\log p(\theta,\mathcal{D}) = \frac{N_H + a - 1}{\theta} - \frac{N_T + b - 1}{1-\theta} = 0 dθdlogp(θ,D)=θNH+a−1−1−θNT+b−1=0
解上面方程得: θ ^ MAP = N H + a − 1 N H + N T + a + b − 2 \hat{\theta}_{\text{MAP}} = \frac{N_H + a - 1}{N_H + N_T + a + b - 2} θ^MAP=NH+NT+a+b−2NH+a−1
所以由这个式子我们也可发现当数据量很大时, N H , N T N_H,N_T NH,NT占主导 θ ^ MAP \hat{\theta}_{\text{MAP}} θ^MAP趋近于MLE。数据很少时,先验拉回中心位置,避免 0 或 1 的极端估计。
下面的表格从实际案例反映了这一点。
| 估计量 | 公式 | NH=2, NT=0 | NH=55, NT=45 |
|---|---|---|---|
| MLE | NH/(NH+NT) | 2/2 = 1.00 | 55/100 = 0.550 |
| 后验期望 | (NH+α)/(NH+NT+α+β) | 4/6 ≈ 0.548 | 57/104 ≈ 0.548 |
| MAP | (NH+α-1)/(NH+NT+α+β-2) | 3/5 = 0.600 | 56/102 ≈ 0.549 |
先验在小数据时起作用,大数据时三者都趋向真实比例。