一、费马小定理
如果 p 是一个素数,并且 a 是一个整数,满足 1<a<p,(即 a 与 p 互质)那么以下同余式成立:
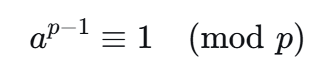
二、费马素数检验
如果存在一个整数 a,使得
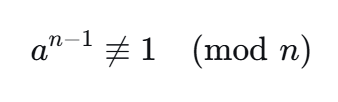
那么 n 一定不是素数
三、Carmichael
费马素数检验最大的缺陷在于存在一种特殊的合数

最小的卡迈克尔数是 561=3×11×17
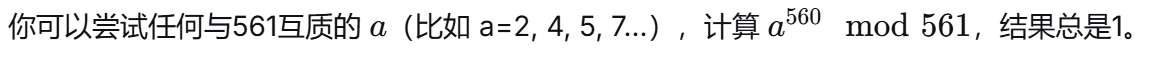
因此,费马检验无法将561识别为合数。
四、欧拉准则
这里要用到先前文章(二次同余式和平方剩余)的勒让德符号
如果 p 是一个奇素数,并且 a 是一个与 p 互质的整数(即 gcd(a,p)=1),那么
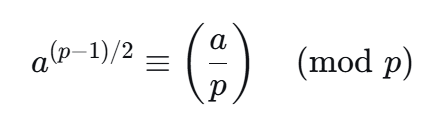
结果为1, a 是模 p 的二次剩余 ;结果为-1,a 是模 p 的二次非剩余
五、欧拉拟素数检验

这个方法能够检测Carmichael!!!

六、Miller-Rabin强拟素数检验
这是目前最强大、最广泛使用的概率性素数检验算法

具体操作步骤可以参考: https://www.bilibili.com/video/BV1T44y1Z7Gx