我们开发了一种独特的模型,用于预测在当前时间起一定分钟数内,某个站点的电动汽车充电端口可用的概率,这有助于电动汽车驾驶员高效地规划行程,同时最大限度地减少在充电站的等待时间。
全球范围内,电动汽车 (EV) 的普及速度正在加快,这也带来了对可靠、稳健的充电基础设施的迫切需求。建设更多实体充电站固然重要,但同样重要的是最大限度地提高基础设施效率,并尽可能减少"里程焦虑"。"里程焦虑"指的是电动汽车驾驶员担心在到达目的地或最近的充电站之前电量耗尽的担忧。基于这些担忧,我们设计了一种电动汽车路线规划方法, 该方法根据电池电量和目的地,将充电站信息整合到导航路线中,从而有效缓解里程焦虑。
我们开发了一款全新的轻量级、高效预测模型,它可以回答核心问题:"在特定站点,电动汽车充电桩在几分钟后可用的概率是多少? " 我们发现,最复杂的模型并非总是最佳解决方案。通过模型和部署基础设施的协同设计,我们基于简单的线性回归方法,创建了一个高效的预测系统。该模型的优势在于其简洁性,它能够利用易于获取的特征,同时在强大的基准模型基础上实现性能提升。我们的工作表明,将直观的现实世界逻辑与机器学习相结合,可以显著提升运营效率和用户体验。
创建模型
我们的目标是在最大限度提高预测能力的同时,尽可能减少特征集(即模型用于进行预测的具体、可测量的数据点),以确保快速部署和低延迟。在测试了包括决策树和简单神经网络在内的各种架构后,我们发现,对于这项特定任务而言,直接的线性回归模型性能最佳、鲁棒性最强。
我们使用充电网络的实时可用性数据训练模型,根据模型特征和权重标准,计算当前观测时间后一定分钟内可用的充电端口真实数量。我们从两个不同的地区(加拿大和德国)均匀抽取端口样本。规模较大的充电站更有可能被纳入训练集,因为它们比孤立的端口流量更大,更能反映实际使用情况。
特征
该模型将一天中的小时作为关键信息("特征")。它将每个小时(或小时范围)分别处理。例如,"上午 9 点"是一个特征,"下午 5 点"是另一个特征。
重量
"权重"是指线性回归算法在训练过程中学习到的具体数值。这些数值决定了一天中每个特定小时对最终预测结果的影响程度。
- 正权重表示在该小时(例如,上午 7:00)期间,港口往往会被占用(占用率正在增加)。
- 负权重意味着在该小时(例如下午 5:00),港口往往会空出来(占用率正在下降)。
- 重量为零或接近零意味着在该小时内(例如凌晨 3:00),港口状态几乎没有变化。
这些"小时特征权重"是模型学习到的系数,用于量化一天中每个小时电动汽车充电桩占用率的可预测变化率。本质上,该模型学习如何将当前可用充电桩数量与未来可用充电桩数量之间的差异表示为小时特征权重的函数。
针对一天中每个小时学习到的特征权重尤其具有启发意义,因为它们直接反映了港口占用率的变化速率。如下图所示,存在与司机排班相关的清晰且可预测的趋势:
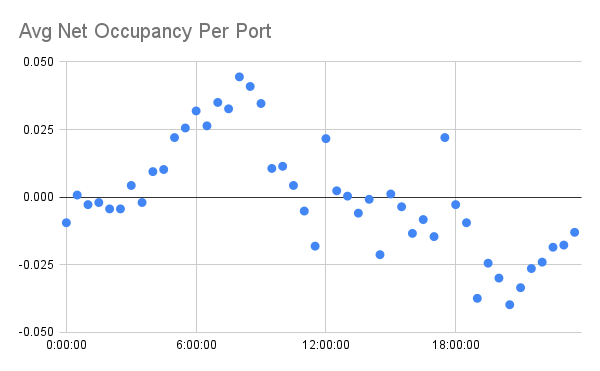
每小时的特征权重(以30分钟为周期)。它们对应于每个30分钟时间段内端口占用率的变化率。
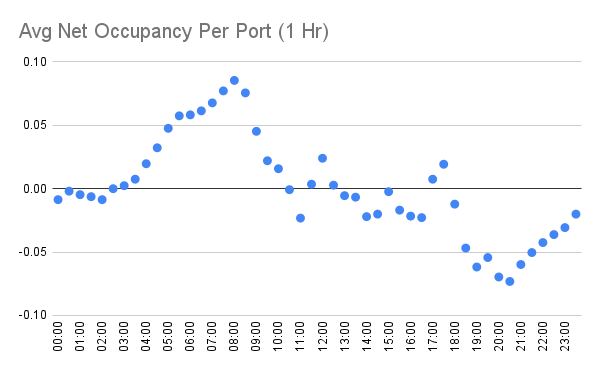
每小时的特征权重(以 60 分钟为时间范围)。它们对应于每个 60 分钟时间段内端口占用率的变化率。
请注意,该模型仅在变化率显著(例如,高峰时段)或站点规模较大(更多端口会放大预测的变化)时才会与当前状态区分开来,而这些正是发布更新预测的正确时机。
实验
我们的评估旨在严谨且能代表实际使用情况。对于 30 分钟和 60 分钟两种时间尺度,我们随机选取 100 个站点,每天(每 30 分钟)对其占用状态进行 48 次采样,持续一周,以评估预测结果。
该模型以一个非常强大的基准模型------"保持当前状态"方法------进行了基准测试。该基准模型简单地假设,在一定分钟数 ( H ) 后,可用端口的数量将与当前数量完全相同。
虽然简单,但这个基准很难被超越,尤其是在短期内。例如,我们的数据显示,在美国东海岸,30分钟内港口可用性状态发生变化的比例从未超过10%。由于大多数情况下状态保持不变,最简单的预测------无变化------在大多数情况下都是正确的,这使得增加预测价值变得极其困难。
我们重点关注两个关键指标来衡量模型预测空闲端口确切数量的准确性:均方误差 (MSE) 和平均绝对误差 (MAE)。MSE/MAE ≥ 1 个空闲端口的比率衡量了用户最关键的二元任务的准确性:"我能否找到至少一个空闲端口(是/否)?"
结果
评估证实,线性回归模型比强大的"保持当前状态"基线模型提供了关键优势,主要体现在能够正确识别入住率高周转率的不常见但至关重要的时刻。
我们从至少拥有 6 个充电端口的充电站中抽取了测试样本,时间跨度为 30 至 60 分钟,这组样本涵盖了城市环境中实际的充电场景。我们评估了该模型预测充电站至少一个充电端口可用性的能力。评估重点关注充电站的类型和时间段,即模型与基准模型出现差异的时段,具体而言,我们关注的是充电站流量变化显著的时段。
下表显示了在变化最大的时间段(上午 8 点和晚上 8 点)中,我们给出错误预测的时间比例(相当于此问题的平均绝对误差)。

比较至少有一个空闲端口的可用性错误率(30 至 60 分钟范围)。
总而言之,部署回归模型使我们能够在早高峰时段减少约 20% 的错误预测,在晚高峰时段减少约 40% 的错误预测。
区域差异
进一步分析表明,虽然各地区港口收放量变化率曲线的形状相似,但变化幅度却存在显著差异,因此需要建立不同的模型。例如,分别针对加利福尼亚州和德国等地区训练模型,其性能优于将所有数据合并在一起,这表明必须考虑各地区独特的电动汽车使用模式。
结论
我们成功开发并部署了一个轻量级的线性回归模型,能够有效预测电动汽车充电端口的可用性。通过专注于模型的简洁性和速度,并与现有基础设施协同设计,我们避免了更复杂、更耗时且通常难以扩展的方法所带来的问题。
由此产生的模型相比强大的"保持当前状态"基线模型,在预测方面具有显著优势,尤其是在交通高峰期。这种优势直接转化为更佳的用户体验:降低焦虑感,优化路线规划,以及提升整体体验,从而支持电动出行的持续发展。未来的工作将着重于扩展预测范围,为长途旅行规划提供更大的价值。