本节目标:
1)了解全局路径规划算法RRT*的基本原理;
2)使用C#实现RRT*算法;
3)使用Winform对RRT*算法进行仿真,更直观理解RRT*算法;
下面是RRT*算法的Winform实现结果,运行程序后,任意点击一个位置,该位置作为开始点,再点击一个位置作为结束点,然后程序会自动从开始点向外搜索,直到搜索到结束点后停止,然后取其中距离最短的路径作为最优路径;
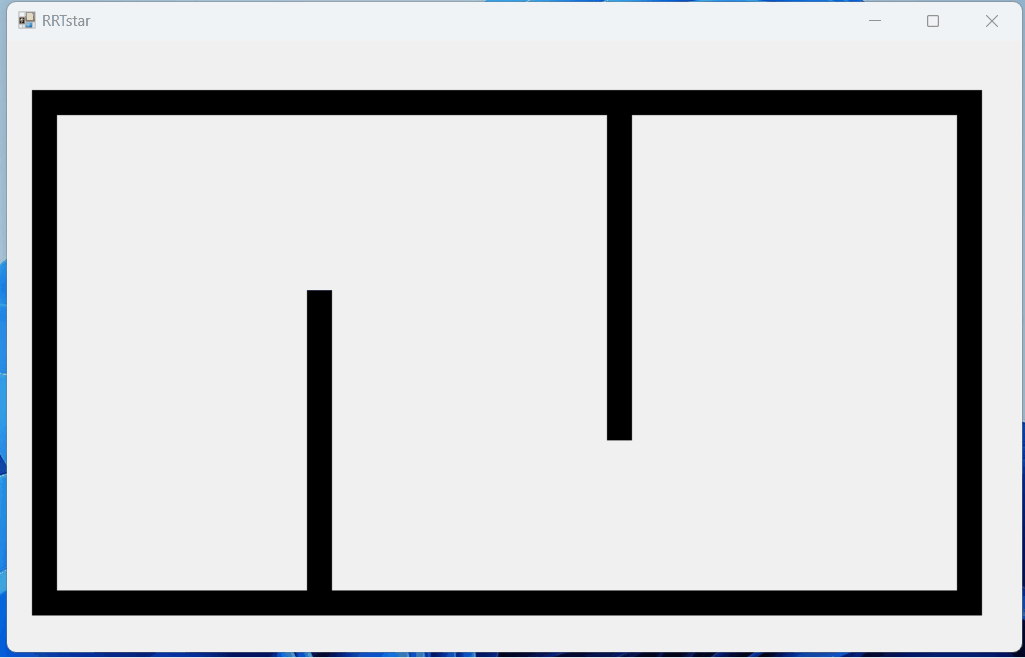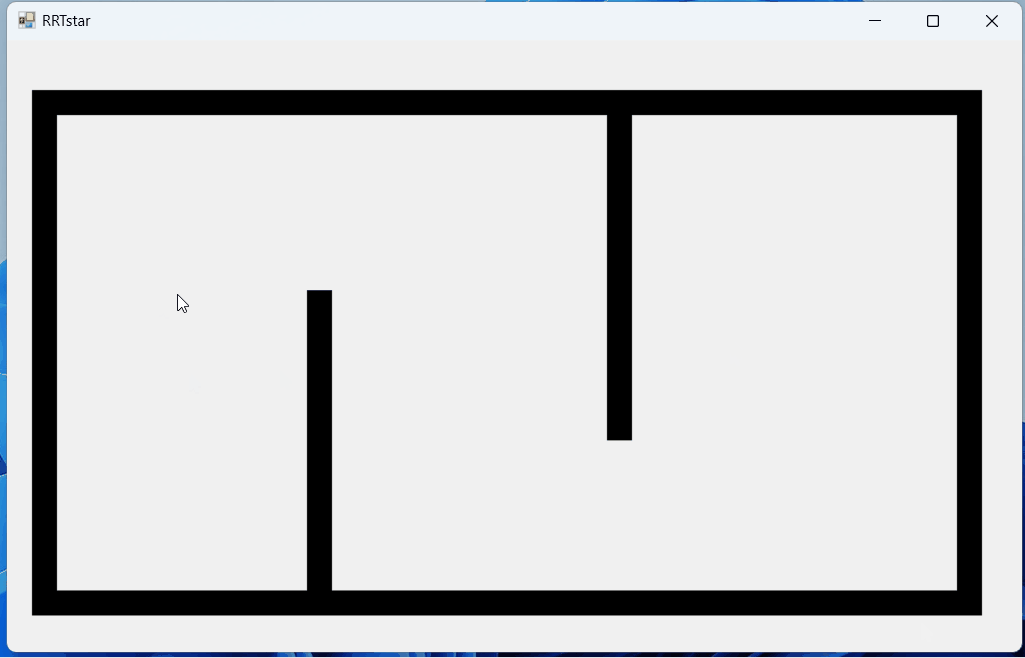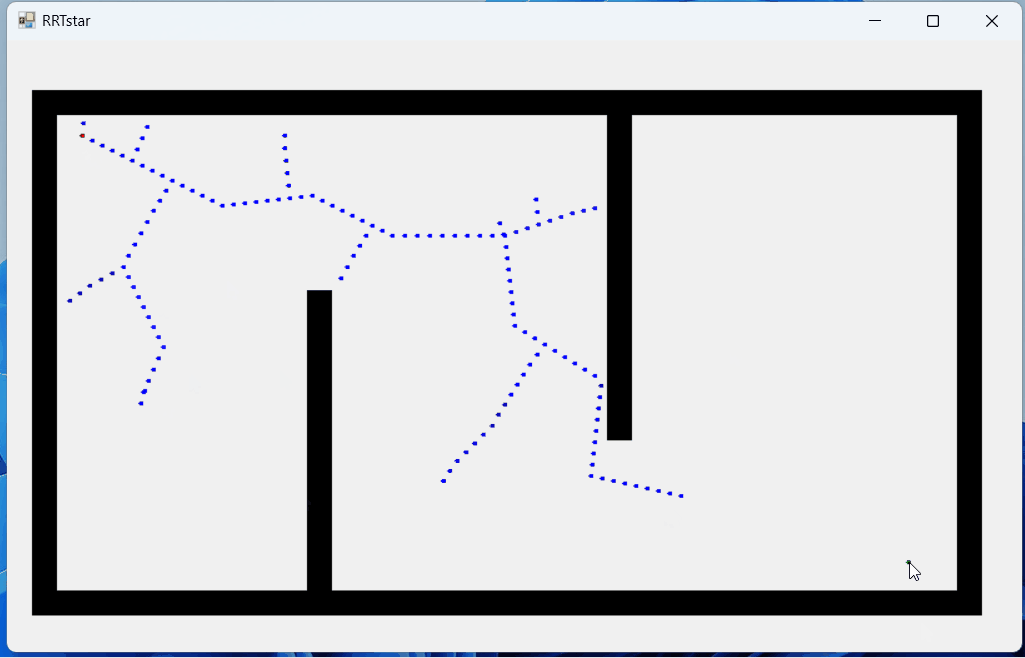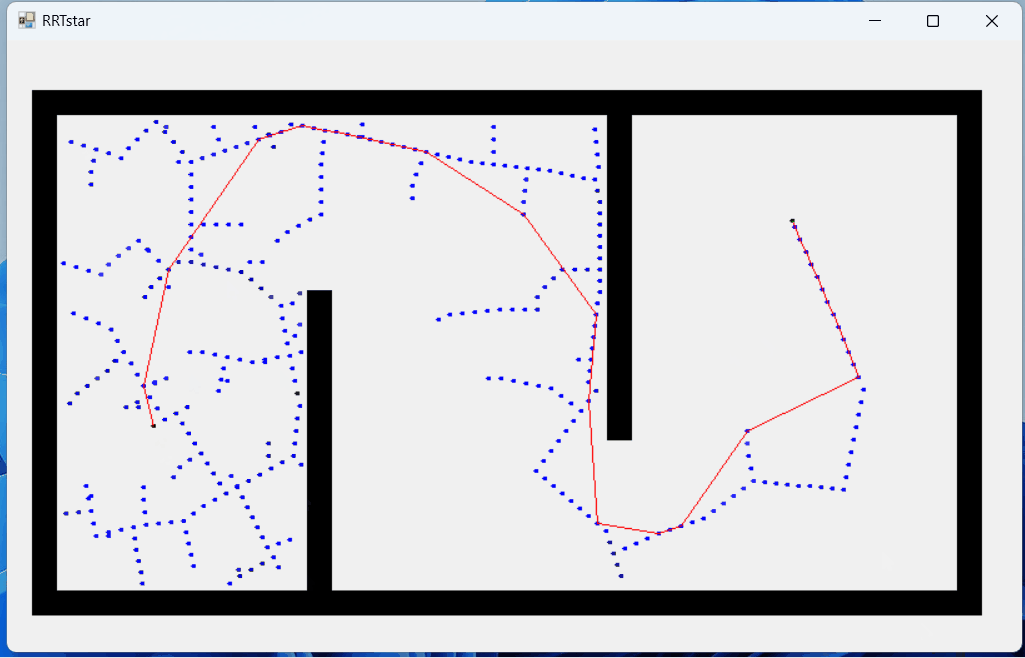
运行环境:
VS2013(.net framework 4.5)
1.1 算法原理
RRT*算法是在高维空间里快速找到一条渐近最优路径的采样型全局路径规划算法。它的核心思想:随机采样 + 树形扩展 + 局部重布线, 一边"长树"一边"剪枝",使路径成本 随采样数增加而单调下降,最终收敛到最优。
RRT*算法实现流程:
1)初始化,把起点加入空树,设好最大采样次数与扩展步长。
2)随机采样,在地图自由空间内随机生成一个采样点。
3)找最近节点,从树中选出离采样点最近的节点。
4)扩展新节点,沿最近节点→采样点方向移动固定步长,得到新节点;若路径碰撞则放弃本轮。
5)选最优父节点,以新节点为中心、给定半径画邻域球,在球内树节点中选出"到达新节点总成本最小"的点作为父节点,把新节点接入树。
6)重布线邻域,检查邻域球内其他节点:若经新节点再到达它们的成本更低,则把它们的父节点改挂到新节点,实现局部成本下降。
7)尝试连接目标,若新节点进入目标区域,将目标直接接入树,得到一条可行路径。
8)迭代与返回,重复 2-7 直到最大采样次数;返回当前最短路径(可随采样继续优化)。
RRT*算法流程图:
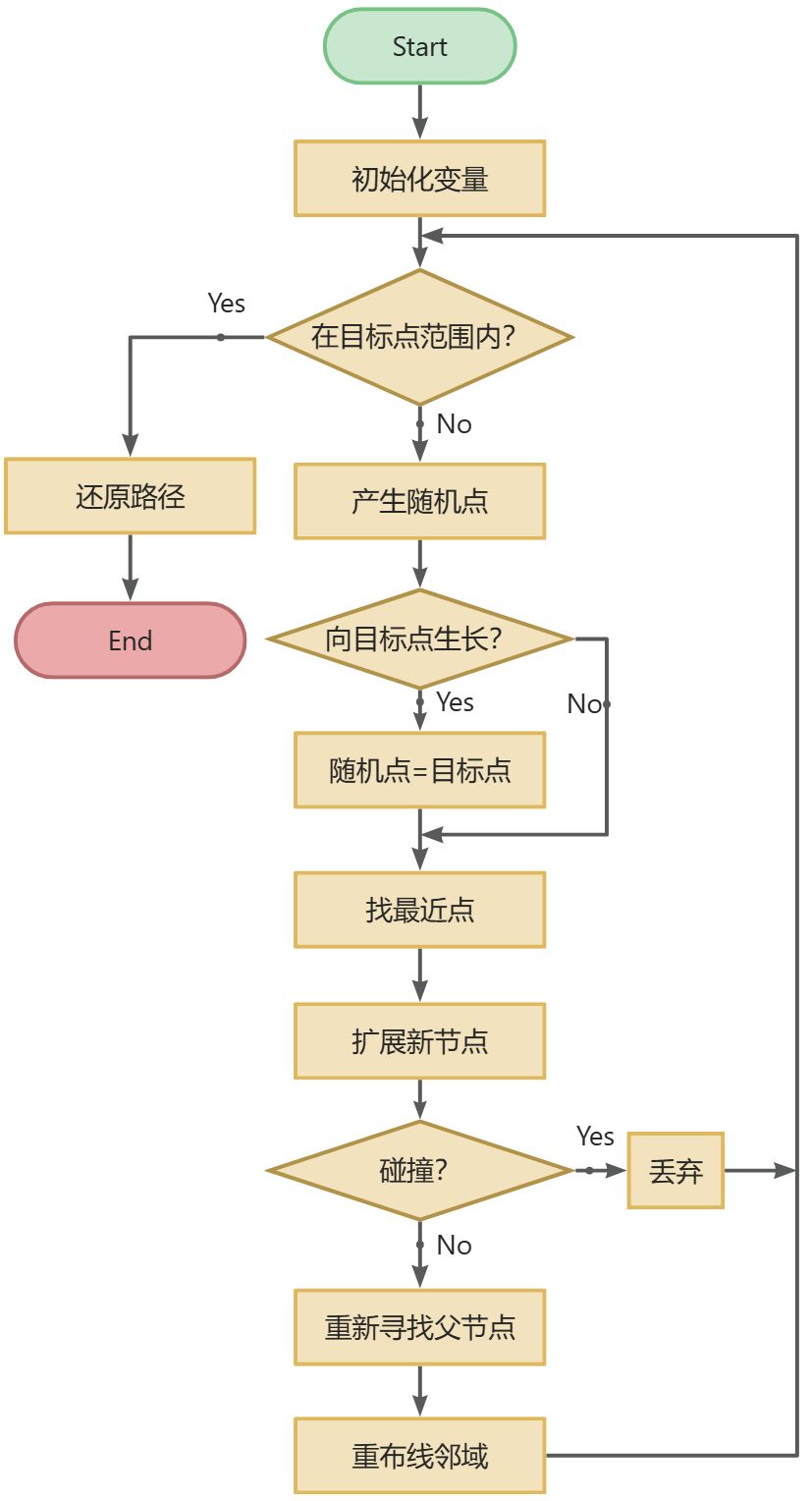
1.2 实现
根据上面对RRT*算法的分析,进行C#程序设计,程序流程图如下;
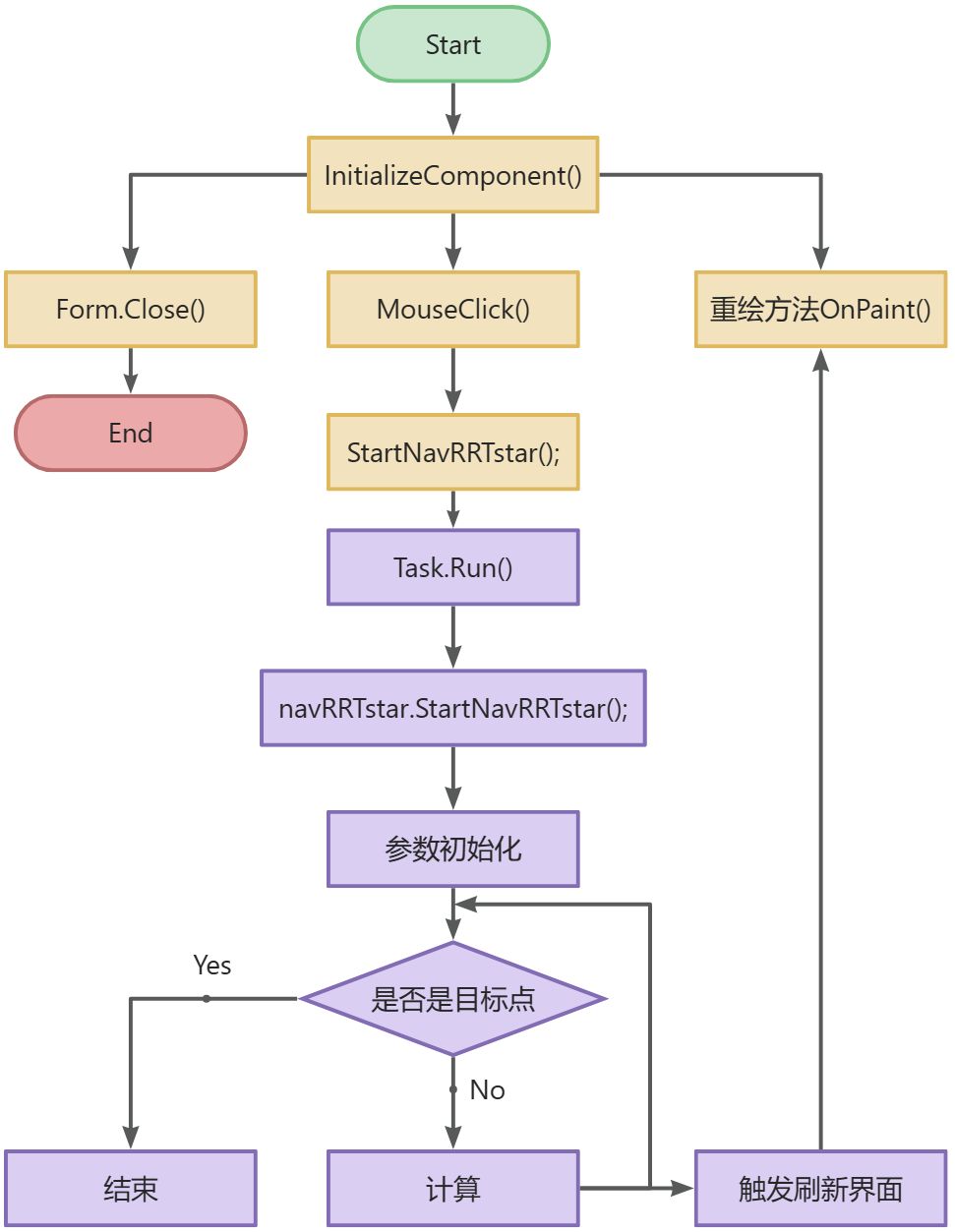
1.2.1 变量
cs
Point[] obstacleStart = new Point[100], obstacleEnd = new Point[100];
NavRRTstar navRRTstar = new NavRRTstar();
bool bStartPointFlg;
bool bGoalPointFlg;
Point Startpoint;
Point Goalpoint;
int paintpix;
int upvalue;1.2.2 障碍物初始化
cs
public Form1()
{
InitializeComponent();
//解决绘图时画面闪烁
SetStyle(ControlStyles.UserPaint, true);
SetStyle(ControlStyles.AllPaintingInWmPaint, true); // 禁止擦除背景.
SetStyle(ControlStyles.DoubleBuffer, true); // 双缓冲
Init();
}
void Init()
{
paintpix = 20;
obstacleStart[0].X = (1 * paintpix);
obstacleStart[0].Y = (2 * paintpix);
obstacleEnd[0].X = (2 * paintpix);
obstacleEnd[0].Y = (23 * paintpix);
obstacleStart[1].X = (38 * paintpix);
obstacleStart[1].Y = (2 * paintpix);
obstacleEnd[1].X = (39 * paintpix);
obstacleEnd[1].Y = (23 * paintpix);
obstacleStart[2].X = (2 * paintpix);
obstacleStart[2].Y = (2 * paintpix);
obstacleEnd[2].X = (38 * paintpix);
obstacleEnd[2].Y = (3 * paintpix);
obstacleStart[3].X = (2 * paintpix);
obstacleStart[3].Y = (22 * paintpix);
obstacleEnd[3].X = (38 * paintpix);
obstacleEnd[3].Y = (23 * paintpix);
obstacleStart[4].X = (24 * paintpix);
obstacleStart[4].Y = (2 * paintpix);
obstacleEnd[4].X = (25 * paintpix);
obstacleEnd[4].Y = (16 * paintpix);
obstacleStart[5].X = (12 * paintpix);
obstacleStart[5].Y = (10 * paintpix);
obstacleEnd[5].X = (13 * paintpix);
obstacleEnd[5].Y = (23 * paintpix);
navRRTstar.OnSignal += this.reponsefunc;
upvalue = 0;
}1.2.3 重绘
cs
protected override void OnPaint(PaintEventArgs e)
{
base.OnPaint(e);
Graphics g= e.Graphics;
//障碍物
for (int m = 0; m <= 5; m++)
rect(obstacleStart[m], obstacleEnd[m], Color.Black,g);
//点
Point openlist=new Point();
if (navRRTstar.bPassPointShowFlg)
{
for (int i = 0; i<navRRTstar.iListNum; i++)
{
openlist.X = (navRRTstar.openlist[i].current.X);
openlist.Y = (navRRTstar.openlist[i].current.Y);
ellipse(openlist, 2, Color.Blue,g);
}
}
//绘制路径
Point qStartPath = new Point(), qEndPath = new Point();
if (navRRTstar.bShowPathFlg)
{
for (int i = 0; i<navRRTstar.iPathNum; i++)
{
qStartPath.X = (navRRTstar.pathlist[i].current.X);
qStartPath.Y = (navRRTstar.pathlist[i].current.Y);
qEndPath.X = (navRRTstar.pathlist[i].parrent.X);
qEndPath.Y = (navRRTstar.pathlist[i].parrent.Y);
line(qStartPath, qEndPath, Color.Red,g);
}
}
//开始点
if (bStartPointFlg)
ellipse(Startpoint, 2, Color.Red,g);
//结束点
if (bGoalPointFlg)
ellipse(Goalpoint, 2, Color.Green,g);
}
void rect(Point startp, Point endp, Color color, Graphics g)
{
SolidBrush brush = new SolidBrush(color);
g.FillRectangle(brush, startp.X, startp.Y, Math.Abs(endp.X - startp.X), Math.Abs(endp.Y - startp.Y));
}
//画椭圆
void ellipse(Point pt, int radius, Color color, Graphics g)
{
SolidBrush brush = new SolidBrush(color);
g.FillEllipse(brush,pt.X - radius, pt.Y - radius, 2 * radius, 2 * radius);
}
//画直线
void line(Point Beg, Point End, Color color,Graphics g)
{
SolidBrush brush = new SolidBrush(color);
Pen pen = new Pen(brush, 1);
g.DrawLine(pen, Beg.X, Beg.Y, End.X, End.Y);
}
void reponsefunc() //槽函数
{
this.Invalidate();
//update();
}1.2.4 鼠标事件
cs
private void Form1_MouseClick(object sender, MouseEventArgs e)
{
if (e.Button == MouseButtons.Left && upvalue == 0)
{
Startpoint.X = (e.X);
Startpoint.Y = (e.Y);
bStartPointFlg = true;
upvalue = 1;
this.Invalidate();
}
else if (e.Button == MouseButtons.Left && upvalue == 1)
{
Goalpoint.X = (e.X);
Goalpoint.Y = (e.Y);
bGoalPointFlg = true;
upvalue = 2;
navRRTstar.startpoint.X = Startpoint.X;
navRRTstar.startpoint.Y = Startpoint.Y;
navRRTstar.goalpoint.X = Goalpoint.X;
navRRTstar.goalpoint.Y = Goalpoint.Y;
for (int m = 0; m <= 5; m++)
{
navRRTstar.obstacleStart[m].X = obstacleStart[m].X;
navRRTstar.obstacleStart[m].Y = obstacleStart[m].Y;
navRRTstar.obstacleEnd[m].X = obstacleEnd[m].X;
navRRTstar.obstacleEnd[m].Y = obstacleEnd[m].Y;
}
StartNavRRTstar();
}
else if (e.Button == MouseButtons.Left && upvalue == 2)
{
bStartPointFlg = false;
bGoalPointFlg = false;
navRRTstar.bPassPointShowFlg = false;
navRRTstar.bShowPathFlg = false;
upvalue = 0;
this.Invalidate();
}
}
void StartNavRRTstar()
{
Task.Run(() =>
{
navRRTstar.StartNavRRTstar();
});
}1.2.5 算法
NavRRTstar.cs
cs
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace Winform_RRTstar
{
class NavRRTstar
{
public bool bPassPointShowFlg;
public int iPathNum;
public bool bShowPathFlg;
public int iListNum;
public listpoint[] openlist = new listpoint[5000];
public listpoint[] pathlist = new listpoint[1000];
public Point startpoint;//开始位置
public Point goalpoint;//结束位置
public Point[] obstacleStart = new Point[10],obstacleEnd = new Point[10]; //障碍物
public event Action OnSignal;//触发更新
int iEndOffset = 12;//到终点的精度
int iStepLength = 10;//步长
int prob = 30;//0-100, 当0<p<Prob的时候,随机树朝目标点生长;当Prob<p<100时,随机树朝一个随机方向生长。
int iStarRadius = 100;//重新找父节点的半径
int iSaftyLength = 4;
int iDelayTime = 1;
public struct listpoint
{
public Point parrent;
public Point current;
public double distance;
/*
public listpoint()
{
parrent = new Point();
current = new Point();
distance = new double();
}*/
}
public void StartNavRRTstar()
{
Point pCurrentPoint = new Point();
bPassPointShowFlg = true;
pCurrentPoint = startpoint;
Point pRandPoint = new Point();//随机点
Point pNearPoint = new Point();//最近点
Point pNewPoint = new Point();//
openlist[0].current = startpoint;
openlist[0].parrent = startpoint;
openlist[0].distance = 0;
iListNum = 1;
int iListMinNum = 0;
double dMinValue = 999999;
double dNearLength=10;
while(Euclid(pCurrentPoint,goalpoint)>=iEndOffset)
{
//随机产生点
Random random = new Random();
pRandPoint.X = random.Next(0, 801);
pRandPoint.Y = random.Next(0, 451);
if(random.Next(0, 101)<prob)
{
pRandPoint = goalpoint;
}
dMinValue = 999999;
for(int i=0;i<iListNum;i++)
{
double xx = Euclid(openlist[i].current,pRandPoint);
if (xx == 0)
xx = 1;
if(xx<dMinValue)
{
iListMinNum = i;
dMinValue = xx;
dNearLength = xx;
}
}
pNearPoint = openlist[iListMinNum].current;
pNewPoint.X = (int)(pNearPoint.X + ((double)iStepLength/dNearLength)*(pRandPoint.X-pNearPoint.X));
pNewPoint.Y = (int)(pNearPoint.Y + ((double)iStepLength/dNearLength)*(pRandPoint.Y-pNearPoint.Y));
//判断是否碰撞
if(!obstacleTest(pNearPoint,pNewPoint))
{
openlist[iListNum].current = pNewPoint;
int distanceMin = (int)(openlist[iListMinNum].distance + Euclid(pNearPoint,pNewPoint));
//RRTstar,重新寻找父节点
bool bRewriteFlg = false;
for(int i=0;i<iListNum;i++)
{
double distanceCurrent = Euclid(openlist[i].current,pNewPoint);
if(distanceCurrent<=iStarRadius)
{
if(openlist[i].distance+distanceCurrent<distanceMin)
{
if(!obstacleTest(openlist[i].current,pNewPoint))
{
distanceMin = (int)(openlist[i].distance+distanceCurrent);
openlist[iListNum].parrent = openlist[i].current;
openlist[iListNum].distance = distanceMin;
bRewriteFlg = true;
}
}
}
}
if(!bRewriteFlg)
{
openlist[iListNum].parrent = pNearPoint;
openlist[iListNum].distance = distanceMin;
}
pCurrentPoint = pNewPoint;
iListNum++;
OnSignal.Invoke();
//emit ASignal();
}
if(Euclid(pCurrentPoint,goalpoint)<=iEndOffset)
{
//搜索结束,还原路线
listpoint listcurrent;
bShowPathFlg = false;
pathlist[0].current = goalpoint;
pathlist[0].parrent = pCurrentPoint;
listcurrent = openlist[iListNum-1];
pathlist[1] = listcurrent;
iPathNum = 2;
while((listcurrent.parrent.X!=startpoint.X)||(listcurrent.parrent.Y!=startpoint.Y))
{
for(int k=0;k<iListNum;k++)
{
if(listcurrent.parrent.X==openlist[k].current.X&&listcurrent.parrent.Y==openlist[k].current.Y)
{
listcurrent = openlist[k];
pathlist[iPathNum] = openlist[k];
iPathNum ++;
break;
}
}
}
bShowPathFlg = true;
OnSignal.Invoke();
//emit ASignal();
break;
}
System.Threading.Thread.Sleep(iDelayTime);
//Delay(iDelayTime);
}
}
double Euclid(Point p1,Point p2)
{
double m;
m = Math.Sqrt(Math.Pow((p1.X - p2.X), 2) + Math.Pow((p1.Y - p2.Y), 2));
return m;
}
bool obstacleTest(Point targetpoint) //碰撞检测
{
bool ishit = false;
for (int m = 0; m <= 5; m++)
{
if (targetpoint.X >= obstacleStart[m].X && targetpoint.X < obstacleEnd[m].X
&& targetpoint.Y >= obstacleStart[m].Y && targetpoint.Y < obstacleEnd[m].Y)
ishit = true;
}
return ishit;
}
bool obstacleTest(Point NearPoint,Point NewPoint)
{
bool isHit = false;
Point CrossPoints = new Point(),CrossPointe = new Point();
bool[] isHit1 = new bool[4];
for(int i=0;i<=5;i++)
{
//两个线段是否相交1.快速排斥计算2.跨立计算
CrossPoints.X = obstacleStart[i].X-iSaftyLength;
CrossPoints.Y = obstacleStart[i].Y-iSaftyLength;
CrossPointe.X = obstacleEnd[i].X+iSaftyLength;
CrossPointe.Y = obstacleStart[i].Y-iSaftyLength;
isHit1[0] =CrossTest(NearPoint,NewPoint,CrossPoints,CrossPointe);
CrossPoints.X = obstacleStart[i].X-iSaftyLength;
CrossPoints.Y = obstacleStart[i].Y-iSaftyLength;
CrossPointe.X = obstacleStart[i].X-iSaftyLength;
CrossPointe.Y = obstacleEnd[i].Y+iSaftyLength;
isHit1[1] =CrossTest(NearPoint,NewPoint,CrossPoints,CrossPointe);
CrossPoints.X = obstacleEnd[i].X+iSaftyLength;
CrossPoints.Y = obstacleStart[i].Y-iSaftyLength;
CrossPointe.X = obstacleEnd[i].X+iSaftyLength;
CrossPointe.Y = obstacleEnd[i].Y+iSaftyLength;
isHit1[2] =CrossTest(NearPoint,NewPoint,CrossPoints,CrossPointe);
CrossPoints.X = obstacleStart[i].X-iSaftyLength;
CrossPoints.Y = obstacleEnd[i].Y+iSaftyLength;
CrossPointe.X = obstacleEnd[i].X+iSaftyLength;
CrossPointe.Y = obstacleEnd[i].Y+iSaftyLength;
isHit1[3] =CrossTest(NearPoint,NewPoint,CrossPoints,CrossPointe);
if(isHit1[0]||isHit1[1]||isHit1[2]||isHit1[3])
isHit = true;
}
return isHit;
}
bool CrossTest(Point p1s,Point p1e,Point p2s,Point p2e)
{
//两个线段相交判断
//1.快速排斥计算
int p1xMax;
int p1xMin;
int p1yMax;
int p1yMin;
int p2xMax;
int p2xMin;
int p2yMax;
int p2yMin;
if(p1s.X>p1e.X){
p1xMax = p1s.X;
p1xMin = p1e.X;
}
else{
p1xMax = p1e.X;
p1xMin = p1s.X;
}
if(p1s.Y>p1e.Y){
p1yMax = p1s.Y;
p1yMin = p1e.Y;
}
else{
p1yMax = p1e.Y;
p1yMin = p1s.Y;
}
if(p2s.X>p2e.X){
p2xMax = p2s.X;
p2xMin = p2e.X;
}
else{
p2xMax = p2e.X;
p2xMin = p2s.X;
}
if(p2s.Y>p2e.Y){
p2yMax = p2s.Y;
p2yMin = p2e.Y;
}
else{
p2yMax = p2e.Y;
p2yMin = p2s.Y;
}
if((p1xMax<p2xMin)||(p1xMin>p2xMax)||(p1yMax<p2yMin)||(p1yMin>p2yMax))
return false;
//2.跨立计算
/*根据上面的公式和右手螺旋法则,如果相交,AB X AC的z坐标值z1与AB X AD的z坐标值z2必然异号;同样的,DC X DA的z坐标值z3与DC X DB的z坐标值z4也必然异号。
特别的,如果B在CD上时,求得的z坐标值是0。所以只要同时满足z1 X z2 ≤ 0,z3 X z4 ≤ 0,就能保证必然相交
AB = (a,b,0),CD = (c,d,0), AB X CD = (0,0,ad-bc)*/
Point pointA = new Point(), pointB = new Point(), pointC = new Point(), pointD = new Point();
pointA = p1s;
pointB = p1e;
pointC = p2s;
pointD = p2e;
int z1,z2,z3,z4;
//AB X AC, AB=(pointB.x - pointA.x,pointB.y - pointA.y) , AC = (pointC.x - pointA.x,pointC.y - pointA.y)
z1 = (pointB.X - pointA.X)*(pointC.Y - pointA.Y)-(pointB.Y - pointA.Y)*(pointC.X - pointA.X);
//AB X AD, AB=(pointB.x - pointA.x,pointB.y - pointA.y) , AD = (pointD.x - pointA.x,pointD.y - pointA.y)
z2 = (pointB.X - pointA.X)*(pointD.Y - pointA.Y)-(pointB.Y - pointA.Y)*(pointD.X - pointA.X);
//CD X CA, CD=(pointD.x - pointC.x,pointD.y - pointC.y) , CA = (pointA.x - pointC.x,pointA.y - pointC.y)
z3 = (pointD.X - pointC.X)*(pointA.Y - pointC.Y)-(pointD.Y - pointC.Y)*(pointA.X - pointC.X);
//CD X CB, CD=(pointD.x - pointC.x,pointD.y - pointC.y) , CB = (pointB.x - pointC.x,pointB.y - pointC.y)
z4 = (pointD.X - pointC.X)*(pointB.Y - pointC.Y)-(pointD.Y - pointC.Y)*(pointB.X - pointC.X);
if((z1*z2<=0)&&(z3*z4<=0))
return true;
else
return false;
}
}
}1.3 运行
运行程序后,任意点击一个位置,该位置作为开始点,再点击一个位置作为结束点,然后程序会自动从开始点向外搜索,直到搜索到结束点后停止,然后取其中距离最短的路径作为最优路径。

RRT*算法是在RRT的基础上引入了路径优化的机制,目标是通过不断优化逼近最优路径。RRT*的关键改进是在扩展树的同时,它会对树中的节点进行重新计算连接来降低路径成本。这种优化特性使得RRT*在理论上具有渐进最优性,即随着采样点数的增加,路径会逐渐趋向于全局最优解。