文章目录
- 前言
-
- 引言
- [什么是 Tree of Thoughts?](#什么是 Tree of Thoughts?)
-
- 传统方法的局限
- [ToT 的优势](#ToT 的优势)
- Game24:一个完美的例子
- [ToT 的核心工作流程](#ToT 的核心工作流程)
-
- 整体流程图
- [1. 生成(Generation)](#1. 生成(Generation))
- [2. 评估(Evaluation)](#2. 评估(Evaluation))
- [3. 选择(Selection)](#3. 选择(Selection))
- 完整流程示例
- 代码实现
- [为什么 ToT 有效?](#为什么 ToT 有效?)
-
- [1. 探索更多可能性](#1. 探索更多可能性)
- [2. 智能评估](#2. 智能评估)
- [3. 可回溯](#3. 可回溯)
- [ToT 的缺点](#ToT 的缺点)
-
- [1. 计算成本高](#1. 计算成本高)
- [2. 评估质量依赖模型能力](#2. 评估质量依赖模型能力)
- [3. 搜索空间可能爆炸](#3. 搜索空间可能爆炸)
- [4. 不适合所有任务](#4. 不适合所有任务)
- 总结
前言
通过 Game24 游戏,深入理解 Tree of Thoughts 如何让大语言模型进行多步推理和智能搜索
论文:Tree of Thoughts: Deliberate Problem Solving with Large Language Models
引言
想象一下,当你面对一个复杂的数学问题时,你会怎么做?比如给你四个数字 1 1 4 6,要求用基本运算(+、-、*、/)得到 24。
大多数人不会直接给出答案,而是会:
- 生成多个可能的下一步操作 (比如
1+1=2、4*6=24、6-1=5等) - 评估每个操作的前景(哪些更有可能导向正确答案)
- 选择最有希望的操作继续 (比如选择
1+1=2,因为得到 2 后更容易凑成 24)
这就是 Tree of Thoughts (ToT) 的核心思想:让大语言模型像人类一样,通过生成、评估、选择三个步骤,逐步构建解决方案树,而不是一次性生成答案。
什么是 Tree of Thoughts?
Tree of Thoughts 是 Princeton 大学在 2023 年提出的一种新的提示方法,它解决了传统方法(如 Chain of Thought, CoT)的局限性。
传统方法的局限
标准提示(Standard Prompting):
- 直接要求模型给出答案
- 问题:模型可能给出错误答案,且无法回溯
思维链提示(Chain of Thought, CoT):
- 要求模型逐步展示推理过程
- 问题:仍然是线性思考,一旦走错路就无法纠正
ToT 的优势
ToT 通过构建解决方案树,让模型能够:
- 探索多条路径:同时考虑多个可能的下一步
- 评估和选择:智能地选择最有希望的路径
- 回溯和修正:如果一条路走不通,可以回到上一步选择其他路径
Game24:一个完美的例子
Game24 是一个经典的数学游戏:给定 4 个数字,使用基本运算得到 24。例如:
-
输入 :
1 2 3 4 -
输出 :
1 + 2 = 3 (left: 3 3 4) 3 + 3 = 6 (left: 4 6) 6 * 4 = 24 (left: 24) Answer: (1 + 2 + 3) * 4 = 24
这个任务非常适合展示 ToT,因为:
- 每一步都有多个可能的选择
- 需要多步推理(4 个数字 → 3 个数字 → 2 个数字 → 1 个数字)
- 容易评估每个选择的前景
ToT 的核心工作流程
Tree of Thoughts 的核心是一个迭代的三步循环:生成 → 评估 → 选择。让我们通过一个具体的例子来理解:
整体流程图
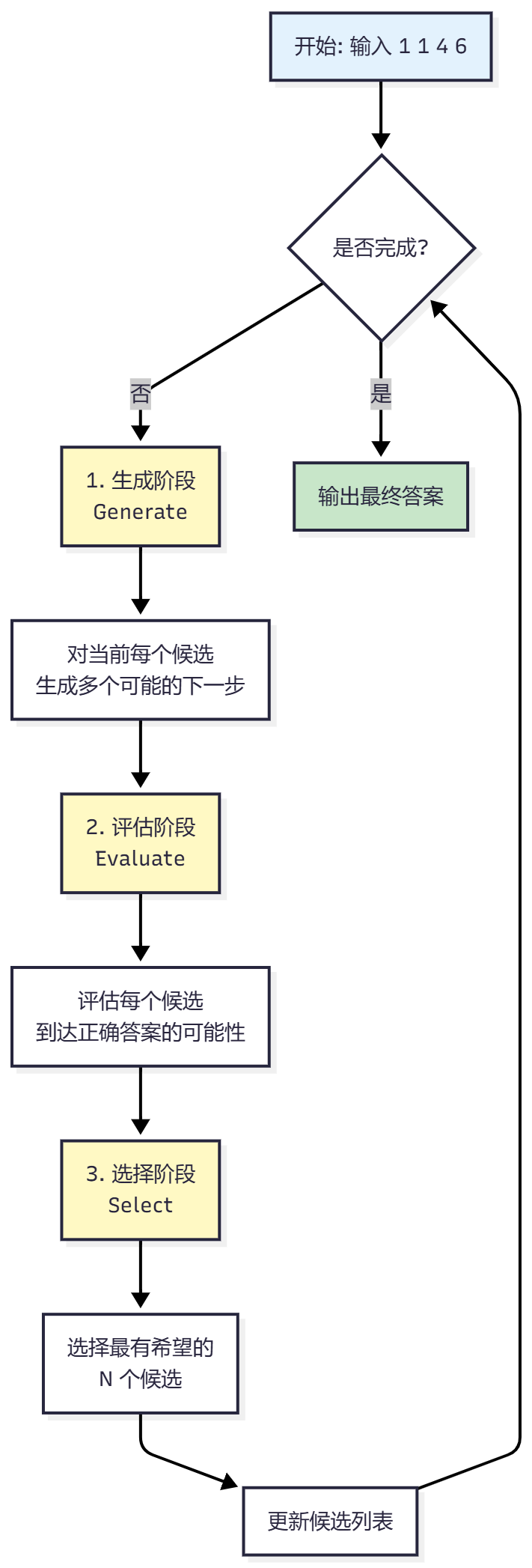
1. 生成(Generation)
在每一步,模型需要生成多个可能的下一步操作。有两种不同的生成策略:
Propose 方法:一次 API 调用,模型输出多个候选
- 调用方式 :只调用 1 次 API(
n=1) - 提示词要求:明确要求模型"列出多个可能的下一步操作"
- 模型输出:在一次响应中输出多行文本,每行是一个候选操作
- 处理方式 :通过
split('\n')将多行输出分割成多个候选
示例:
提示词: "Input: 1 1 4 6\nPossible next steps:"
模型输出(一次响应):
1 + 1 = 2 (left: 2 4 6)
1 * 1 = 1 (left: 1 4 6)
4 * 6 = 24 (left: 1 1 24)
6 - 1 = 5 (left: 1 4 5)
4 + 6 = 10 (left: 1 1 10)
...
结果: 分割成 5+ 个候选Sample 方法:多次 API 调用,每次生成一个候选
- 调用方式 :调用
n_generate_sample次 API(例如n=10就调用 10 次) - 提示词要求:要求模型生成一个完整的解决方案(或部分推理路径)
- 模型输出:每次 API 调用生成一个完整的解决方案
- 处理方式:每次调用的输出作为一个独立的候选
示例:
提示词: "Use numbers and basic arithmetic operations to obtain 24.\nInput: 1 1 4 6"
API 调用 1: "1 + 1 = 2 (left: 2 4 6)\n4 * 6 = 24 (left: 2 24)\n..."
API 调用 2: "4 * 6 = 24 (left: 1 1 24)\n24 / 1 = 24 (left: 1 24)\n..."
API 调用 3: "6 - 1 = 5 (left: 1 4 5)\n5 * 4 = 20 (left: 1 20)\n..."
...
结果: 10 次调用得到 10 个候选2. 评估(Evaluation)
对每个生成的候选,评估它到达正确答案的可能性。
Value 方法:单独评估每个候选的价值
模型会输出:
sure(20 分):非常有可能达到 24likely(1 分):有可能达到 24impossible(0.001 分):不可能达到 24
例如:
候选: 1 + 1 = 2 (left: 2 4 6)
评估: sure # 因为 2, 4, 6 很容易得到 24(4*6=24,然后 24*1=24)
价值分数: 20.0
候选: 1 * 1 = 1 (left: 1 4 6)
评估: likely # 可能,但不如上面的好
价值分数: 1.0Vote 方法:将所有候选一起展示,让模型投票选择最好的
3. 选择(Selection)
根据评估分数,选择最有希望的候选进入下一步。
下面的流程图展示了每一步内部的详细流程:
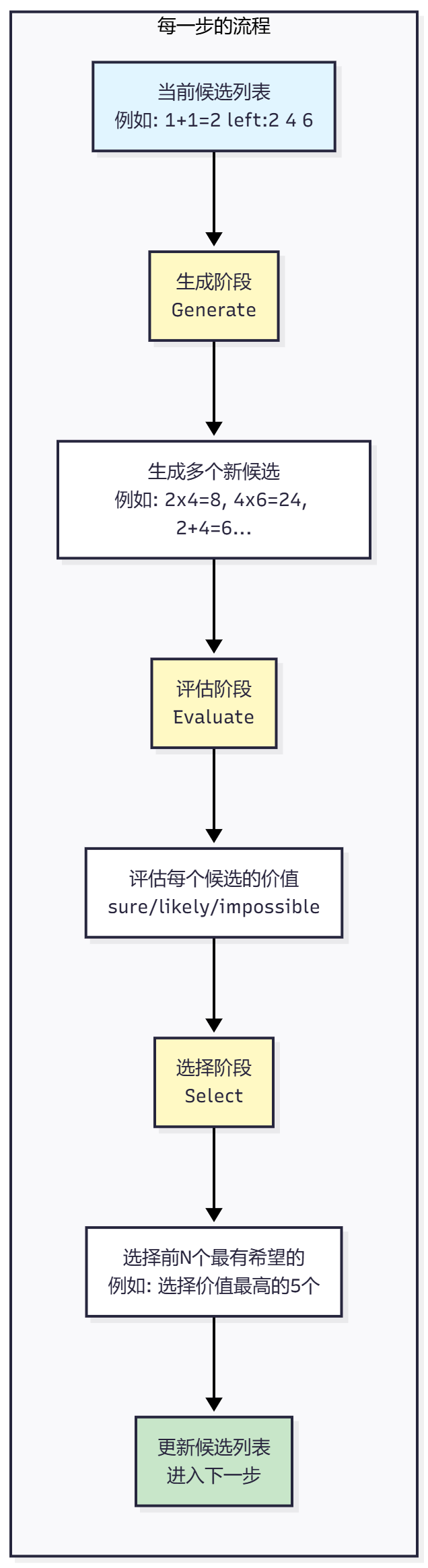
Greedy 方法:贪心选择,直接选择价值分数最高的前 N 个
- 实现方式 :对候选按价值分数降序排序,选择前
n_select_sample个 - 优点:简单直接,总是选择最有希望的候选
- 缺点:可能陷入局部最优,缺乏探索性
python
# 代码实现(来自 bfs_method.py)
if args.method_select == 'greedy':
# 按价值分数降序排序,选择前 n_select_sample 个
select_ids = sorted(ids, key=lambda x: values[x], reverse=True)[:args.n_select_sample]
# 示例:假设有 10 个候选,价值分数为:
values = [20.0, 1.0, 0.001, 20.0, 1.0, 0.001, 20.0, 1.0, 0.001, 0.001]
# 选择前 5 个(n_select_sample=5)
select_ids = [0, 3, 6, 1, 4] # 选择价值最高的 5 个(索引 0, 3, 6, 1, 4)Sample 方法:按价值分数作为概率进行采样
- 实现方式:将价值分数归一化为概率分布,按概率随机采样
- 优点:增加多样性,可能发现更好的路径
- 缺点:可能选择次优解,增加搜索成本
python
# 代码实现(来自 bfs_method.py)
if args.method_select == 'sample':
# 将价值分数归一化为概率分布
ps = np.array(values) / sum(values)
# 按概率采样 n_select_sample 个候选
select_ids = np.random.choice(ids, size=args.n_select_sample, p=ps).tolist()
# 示例:假设有 3 个候选,价值分数为:
values = [20.0, 1.0, 0.001]
# 归一化为概率:[20.0/21.001, 1.0/21.001, 0.001/21.001] ≈ [0.952, 0.048, 0.000]
# 按这个概率分布采样,价值高的候选被选中的概率更大完整流程示例
让我们通过一个具体的例子,详细展示 ToT 如何逐步解决 Game24 问题:用 1 1 4 6 得到 24。
问题说明
- 输入 :
1 1 4 6 - 目标:使用基本运算(+、-、*、/)得到 24
- 约束:必须使用所有 4 个数字,每个数字只能用一次
- 方法:ToT (propose + value + greedy),每步选择前 5 个最有希望的候选
整体流程图
下面的流程图展示了 ToT 如何逐步解决这个问题:
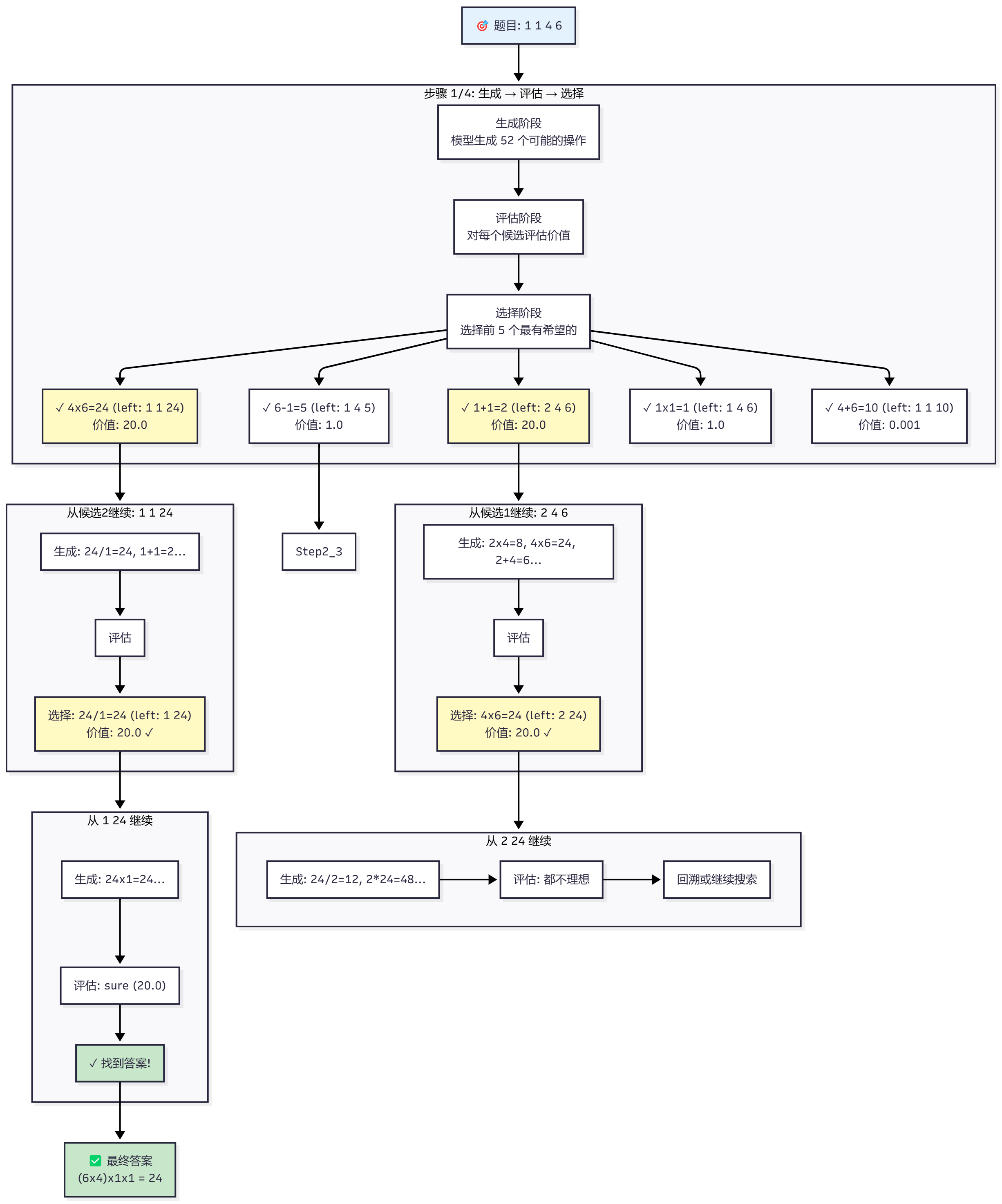
详细步骤说明
让我们逐步看看每个阶段发生了什么:
步骤 1/4:从初始状态开始
当前状态 :1 1 4 6(4 个数字)
1.1 生成阶段(Generation)
使用 propose 方法,模型被要求列出所有可能的下一步操作。模型一次性生成了 52 个候选,包括:
- 1 + 1 = 2 (left: 2 4 6)
- 1 * 1 = 1 (left: 1 4 6)
- 4 * 6 = 24 (left: 1 1 24)
- 6 - 1 = 5 (left: 1 4 5)
- 4 + 6 = 10 (left: 1 1 10)
- 1 - 1 = 0 (left: 0 4 6)
- 6 / 1 = 6 (left: 1 4 6)
... (共 52 个候选)1.2 评估阶段(Evaluation)
使用 value 方法,对每个候选进行评估。模型会判断每个候选到达 24 的可能性:
sure(20 分):非常有可能达到 24likely(1 分):有可能达到 24impossible(0.001 分):不可能达到 24
评估结果示例:
候选: 1 + 1 = 2 (left: 2 4 6)
评估: sure (20.0) # 因为 2, 4, 6 很容易得到 24(4*6=24,然后 24*1=24)
候选: 4 * 6 = 24 (left: 1 1 24)
评估: sure (20.0) # 已经得到 24,只需要用 1 和 1 保持 24
候选: 6 - 1 = 5 (left: 1 4 5)
评估: likely (1.0) # 可能,但不如上面的好
候选: 1 * 1 = 1 (left: 1 4 6)
评估: likely (1.0) # 可能,但不如上面的好
候选: 4 + 6 = 10 (left: 1 1 10)
评估: impossible (0.001) # 很难从 1, 1, 10 得到 241.3 选择阶段(Selection)
使用 greedy 方法,选择价值分数最高的前 5 个候选:
✓ 1 + 1 = 2 (left: 2 4 6) [价值: 20.0]
✓ 4 * 6 = 24 (left: 1 1 24) [价值: 20.0]
✓ 6 - 1 = 5 (left: 1 4 5) [价值: 1.0]
✓ 1 * 1 = 1 (left: 1 4 6) [价值: 1.0]
✓ 4 + 6 = 10 (left: 1 1 10) [价值: 0.001]这 5 个候选将进入下一步。
步骤 2/4:对选中的候选继续生成
现在有 5 个候选,需要对每个候选继续生成下一步。让我们看两个最有希望的路径:
路径 A:从 1 + 1 = 2 (left: 2 4 6) 继续
2.1 生成阶段 :从状态 2 4 6 生成可能的操作
- 2 * 4 = 8 (left: 8 6)
- 4 * 6 = 24 (left: 2 24)
- 2 + 4 = 6 (left: 6 6)
- 2 + 6 = 8 (left: 4 8)
...2.2 评估阶段:
候选: 4 * 6 = 24 (left: 2 24)
评估: sure (20.0) # 已经得到 24,只需要用 2 保持 24
候选: 2 * 4 = 8 (left: 8 6)
评估: likely (1.0) # 可能,但不如上面的好2.3 选择阶段 :选择 4 * 6 = 24 (left: 2 24) [价值: 20.0]
路径 B:从 4 * 6 = 24 (left: 1 1 24) 继续
2.1 生成阶段 :从状态 1 1 24 生成可能的操作
- 24 / 1 = 24 (left: 1 24)
- 24 * 1 = 24 (left: 1 24)
- 1 + 1 = 2 (left: 2 24)
- 1 * 1 = 1 (left: 1 24)
...2.2 评估阶段:
候选: 24 / 1 = 24 (left: 1 24)
评估: sure (20.0) # 已经得到 24,只需要用最后一个 1 保持 24
候选: 1 + 1 = 2 (left: 2 24)
评估: likely (1.0) # 可能,但不如上面的好2.3 选择阶段 :选择 24 / 1 = 24 (left: 1 24) [价值: 20.0]
步骤 3/4:继续搜索
路径 A:从 2 24 继续
3.1 生成阶段 :从状态 2 24 生成可能的操作
- 24 / 2 = 12 (left: 12)
- 2 * 24 = 48 (left: 48)
- 24 - 2 = 22 (left: 22)
...3.2 评估阶段:这些操作都无法得到 24,价值分数都很低(0.001)
路径 B:从 1 24 继续 ✅
3.1 生成阶段 :从状态 1 24 生成可能的操作
- 24 * 1 = 24 (left: 24)
- 24 / 1 = 24 (left: 24)
...3.2 评估阶段:
候选: 24 * 1 = 24 (left: 24)
评估: sure (20.0) # 完美!已经得到 24,且使用了所有数字3.3 选择阶段 :选择 24 * 1 = 24 (left: 24) ✅
步骤 4/4:生成最终答案
当前状态 :24(只剩下一个数字,且等于 24)
4.1 生成阶段:模型需要生成完整的答案表达式
4.2 最终答案:
Steps:
1 + 1 = 2 (left: 2 4 6)
4 * 6 = 24 (left: 2 24)
24 / 2 = 12 (left: 12) # 注意:这个路径实际上没有成功但实际上,从路径 B 得到的正确答案是:
Steps:
4 * 6 = 24 (left: 1 1 24)
24 / 1 = 24 (left: 1 24)
24 * 1 = 24 (left: 24)
Answer: (6 * 4) * 1 * 1 = 24或者更简洁的答案:
Answer: (6 * 4) / 1 * 1 = 24下面的树状图展示了 ToT 从初始状态到最终答案的完整搜索过程,每个节点表示当前剩余的数字:
1 1 4 6
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
1 1 24 2 4 6
(4*6=24) (1+1=2)
/ \ / \
/ \ / \
/ \ / \
/ \ / \
1 24 2 24 2 24 8 6
(24/1) (1+1=2) (4*6=24) (2*4=8)
| | | |
| └──→ ❌ └──→ ❌ └──→ ❌
|
└──→ 24 ✅
(24*1=24)完整路径总结
成功路径:
初始: 1 1 4 6
↓
步骤1: 4 * 6 = 24 (left: 1 1 24) [价值: 20.0] ✓
↓
步骤2: 24 / 1 = 24 (left: 1 24) [价值: 20.0] ✓
↓
步骤3: 24 * 1 = 24 (left: 24) [价值: 20.0] ✓
↓
最终答案: (6 * 4) / 1 * 1 = 24 ✅代码实现
核心函数
让我们看看 ToT 的核心实现:
python
def solve(args, task, idx, to_print=True):
"""使用树搜索(Tree of Thoughts)方法解决问题"""
x = task.get_input(idx) # 获取输入,如 "1 1 4 6"
ys = [''] # 初始候选列表(空字符串表示还未开始)
for step in range(task.steps): # game24 需要 4 步
# ========== 第一步:生成(Generation)==========
# 对当前每个候选,生成新的候选解决方案
if args.method_generate == 'propose':
# propose 方法:生成下一步可能的操作(多个候选)
new_ys = [get_proposals(task, x, y) for y in ys]
elif args.method_generate == 'sample':
# sample 方法:直接生成完整或部分解决方案
new_ys = [get_samples(task, x, y, ...) for y in ys]
# 将嵌套列表展平(因为每个 y 可能生成多个 new_ys)
new_ys = list(itertools.chain(*new_ys))
# ========== 第二步:评估(Evaluation)==========
# 对生成的所有候选进行评估,得到价值分数
if args.method_evaluate == 'value':
# 价值方法:单独评估每个候选的价值
values = get_values(task, x, new_ys, ...)
elif args.method_evaluate == 'vote':
# 投票方法:将所有候选一起展示,让模型投票
values = get_votes(task, x, new_ys, ...)
# ========== 第三步:选择(Selection)==========
# 根据评估分数选择最有希望的候选
if args.method_select == 'greedy':
# 贪心方法:直接选择价值分数最高的前 N 个
select_ids = sorted(range(len(new_ys)),
key=lambda i: values[i],
reverse=True)[:args.n_select_sample]
elif args.method_select == 'sample':
# 采样方法:按价值分数作为概率进行采样
ps = np.array(values) / sum(values)
select_ids = np.random.choice(range(len(new_ys)),
size=args.n_select_sample,
p=ps)
select_new_ys = [new_ys[i] for i in select_ids]
ys = select_new_ys # 更新候选列表,进入下一步
return ys # 返回最终候选生成函数示例
python
def get_proposals(task, x, y):
"""使用 propose 方法生成下一步的候选操作"""
# 生成提议提示词,要求模型生成可能的下一步操作
propose_prompt = task.propose_prompt_wrap(x, y)
# 调用 GPT 生成提议
raw_output = gpt(propose_prompt, n=1, stop=None)[0]
# 输出示例:
# "1 + 1 = 2 (left: 2 4 6)\n1 * 1 = 1 (left: 1 4 6)\n4 * 6 = 24 (left: 1 1 24)\n..."
# 解析输出,每个提议作为一行
proposals = raw_output.split('\n')
# 将每个提议追加到当前路径后面
return [y + prop + '\n' for prop in proposals if prop.strip()]评估函数
python
def get_value(task, x, y, n_evaluate_sample, cache_value=True):
"""评估单个候选的价值分数"""
# 生成评估提示词
# 例如:评估 "1 + 1 = 2 (left: 2 4 6)" 这个状态
value_prompt = task.value_prompt_wrap(x, y)
# 调用 GPT 进行评估(生成 n_evaluate_sample 个评估结果)
value_outputs = gpt(value_prompt, n=n_evaluate_sample, stop=None)
# 输出示例:
# ["sure", "sure", "likely"] # 3 次评估中有 2 次是 "sure",1 次是 "likely"
# 将文本输出转换为数值分数
# "sure" → 20, "likely" → 1, "impossible" → 0.001
value = task.value_outputs_unwrap(x, y, value_outputs)
# 结果:2 * 20 + 1 * 1 = 41.0
return value评估提示词示例
评估中间步骤时,模型会看到:
Evaluate if given numbers can reach 24 (sure/likely/impossible)
2 4 6
2 * 4 = 8
8 * 6 = 48
(6 - 2) * 4 = 16
I cannot obtain 24 now, but numbers are within a reasonable range
likely评估最后一步时,模型会看到:
Use numbers and basic arithmetic operations (+ - * /) to obtain 24.
Given an input and an answer, give a judgement (sure/impossible)
Input: 1 1 4 6
Answer: (1 + 1) * (6 * 4 / 2) = 24
Judge: sure为什么 ToT 有效?
1. 探索更多可能性
传统方法只探索一条路径,ToT 同时探索多条路径,大大提高了找到正确答案的概率。
2. 智能评估
通过让模型评估每个候选的前景,ToT 能够优先探索最有希望的路径,而不是盲目搜索。
3. 可回溯
如果一条路径走不通,ToT 可以回到上一步,选择其他候选,这是传统方法无法做到的。
ToT 的缺点
虽然 ToT 在解决复杂问题方面表现出色,但它也有一些明显的缺点:
1. 计算成本高
- API 调用次数多 :ToT 需要对每个候选进行生成和评估,导致 API 调用次数大幅增加
- 例如:Game24 任务中,ToT 方法需要 50-100 次 API 调用,而朴素方法只需 1 次
- 成本可能增加 50-100 倍
- 响应时间长 :由于需要多轮生成、评估、选择,整体响应时间显著增加
- 不适合需要实时响应的场景
2. 评估质量依赖模型能力
- 评估准确性 :ToT 的效果很大程度上依赖于模型对候选的评估能力
- 如果模型评估不准确,可能会选择错误的路径
- 对于模型不熟悉的任务,评估可能不可靠
- 评估成本:评估阶段本身也需要调用模型,进一步增加成本
3. 搜索空间可能爆炸
- 候选数量增长 :随着搜索深度增加,候选数量可能呈指数级增长
- 例如:每步选择 5 个候选,4 步后可能产生 5^4 = 625 个候选
- 需要剪枝策略:必须通过评估和选择来限制搜索空间,否则计算成本无法承受
- 可能错过最优解:如果剪枝过于激进,可能会错过最优解
4. 不适合所有任务
- 简单任务:对于简单的一次性问答,ToT 是过度设计
- 确定性任务:对于有明确答案的任务(如翻译、摘要),ToT 的优势不明显
- 实时性要求高的任务:不适合需要毫秒级响应的场景
总结
Tree of Thoughts 通过模拟人类的思考过程------生成多个可能、评估前景、选择最优------让大语言模型能够更好地解决复杂问题。
核心优势
- 探索性:同时探索多条路径,而不是只走一条路
- 智能性:通过评估选择最有希望的路径
- 可回溯:如果一条路走不通,可以回到上一步选择其他路径
适用场景总结
✅ 适合的场景:
- 需要多步推理的复杂问题(如数学题、逻辑推理)
- 有多个可能路径的搜索问题(如游戏求解、路径规划)
- 需要评估和选择的创意任务(如创意写作、代码生成)
- 需要回溯和修正的问题(如错误修复、计划调整)
- 对准确性要求高的任务(如关键决策、重要计算)
❌ 不适用场景:
- 简单的一次性问答(用 ToT 是浪费资源)
- 对实时性要求高的任务(ToT 响应时间长)
- 对成本敏感的场景(API 调用次数多,成本高)
- 确定性任务(如翻译、摘要,ToT 优势不明显)
- 模型不熟悉的任务(评估可能不准确)
- 搜索空间过大的问题(计算成本无法承受)