PCA主成分分析法(PCA降维算法)
如何从成绩单中,快速识别出哪些理科强哪些文科强
例子1:首先,在三维坐标系中寻找一条过原点的直线,空间上的所有数据点向这跟直线上投影,投影后的数据点必须方差最大(数据点在这跟直线的间隔必须最大)
然后,再找一根直线,这跟直线必须与它垂直,且满足同样的要求
然后,用两个直线作为一个二维平面的横轴和纵轴,成功把三维降到二维数据,可以把坐标轴一个当作理科综合成绩和文科综合成绩
例子2:随机挑出你的4个同学,不告诉他们是谁,只给你他们的信息让你分辨
如果给你身高信息可能相差不大无法分辨,但如果给你姓氏首字母,则四个数据点之间的间隔会更大------ 信息量大、方差最大
PCA算法的详细算法步骤和过程:
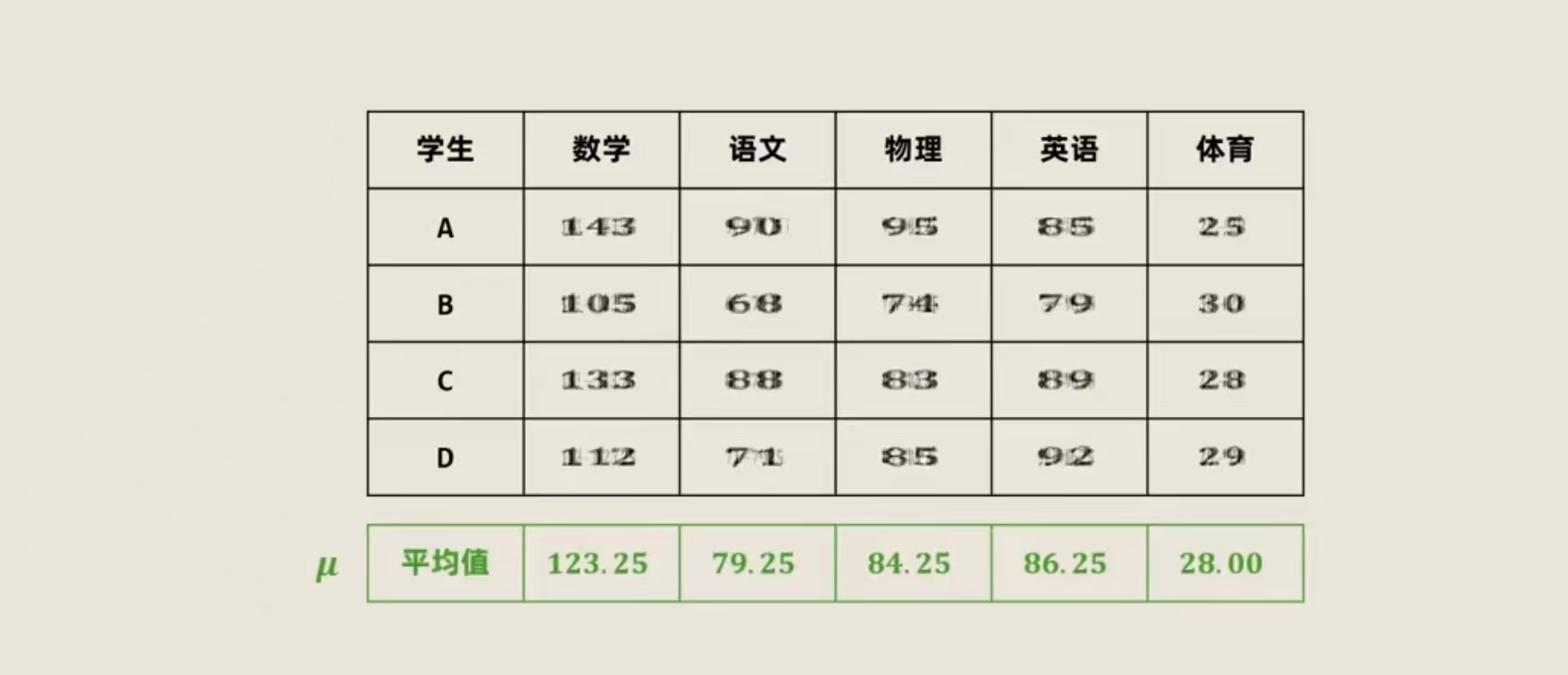
原始数据中不同科目的成绩范围不同
**去中心化:**首先计算每个科目的平均成绩,然后用每个同学的成绩去减去对应科目的平均成绩
(找到原始数据的中心点,整体移动数据的分布,将中心点对准坐标轴原点)
然后把减去平均值的数据分别进行平方运算,在彼此相加除以4-1,这组新数据叫做方差,开方为标准差
标准化的数据:(原始成绩-平均值)/ 标准差
计算每个科目与每个科目的相关性:例如语文和数学的相关性,将数学和语文的标准化数据相乘,再将A B C D相乘的结果分别相加之后除以4-1
数据是正的两个科目的成绩是正相关的,数学成绩好的同学语文成绩也不错;数据是负的两个科目是负相关的;数值是0,说明两个成绩毫不相关
计算特征值和特征向量

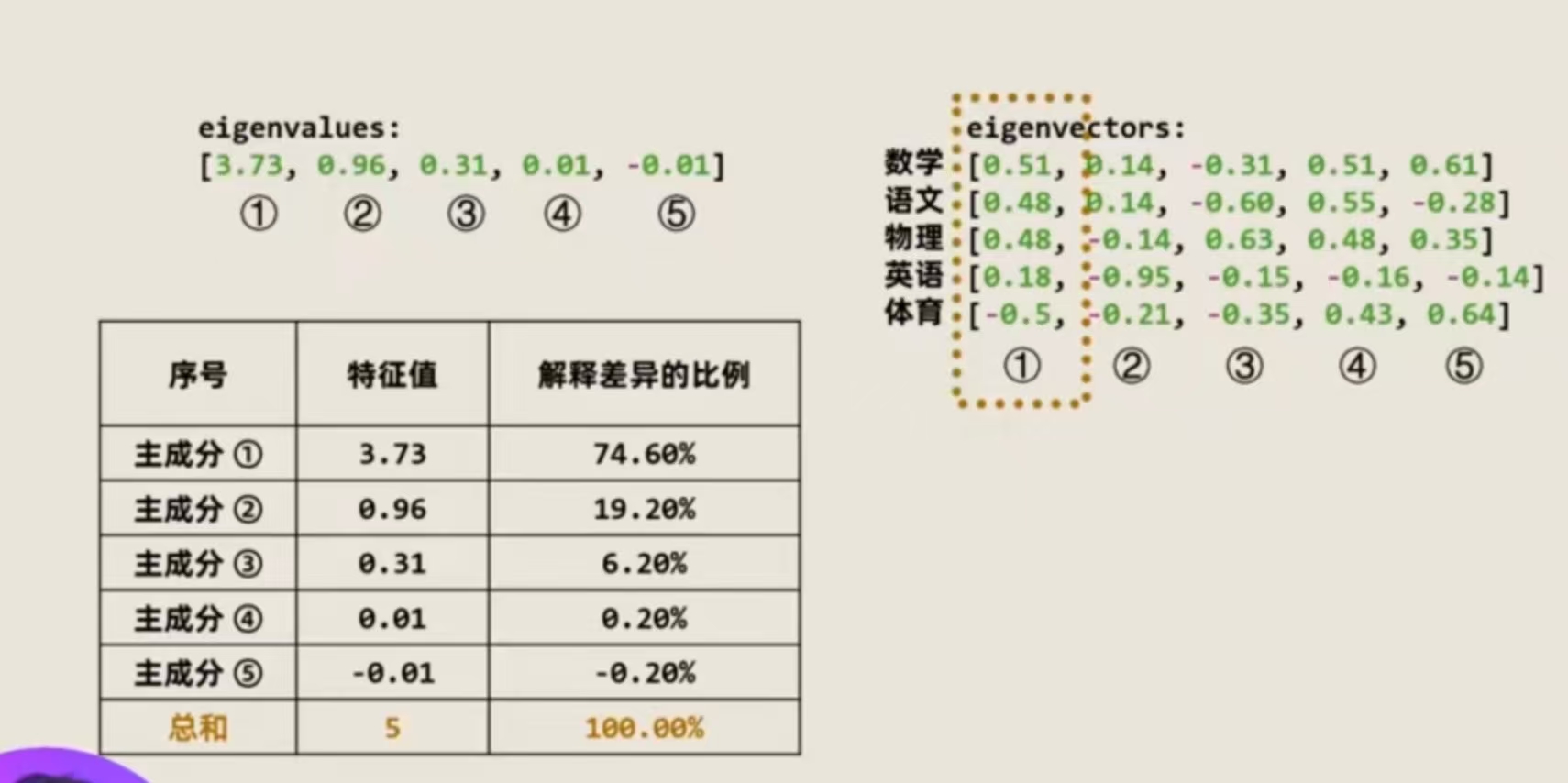
每个特征值对应一组特征向量,特征值代表着他对应的特征向量,可以解释数据之间的差异性程度。比如特征值最大的3.73,如果用他对应的特征向量去降维成绩数据,那么降维后的数据能保留原始成绩数据的74.60%的信息量,由于它保留的数据量最多,我们拿它当作主成分 1;然后是主成分 2,0.96。这就是我们要在三维坐标空间中的那两根直线,用这两根直线作为二维坐标系当中的横轴和纵轴。
主成分 1:它提取了数学、语文、物理的成分很多,所以可以看作是理科+文科综合成绩
主成分 2:英语成绩为负,但绝对值最大,这代表主成分 2利用英语的成绩抽取了更多的成分,所以英语成绩差的同学可以在坐标系中得到很好的体现
降维:
用主成分 1的特征向量分别与一个同学的每个科目相乘,然后彼此相加
同理主成分 2
主成分1为横轴,主成分2为纵轴,最后在二维坐标中可以得到,4个同学的成绩的综合分布了