目录
- [1. 二分分类](#1. 二分分类)
- [2. logistic回归](#2. logistic回归)
- [3. logistic回归损失函数](#3. logistic回归损失函数)
- [4. 梯度下降法](#4. 梯度下降法)
- [5. 导数](#5. 导数)
- [6. 计算图](#6. 计算图)
- [7. 计算图的导数计算](#7. 计算图的导数计算)
- [8. logistic回归中的梯度下降法](#8. logistic回归中的梯度下降法)
- [9. m个样本的梯度下降](#9. m个样本的梯度下降)
- [10. 向量化](#10. 向量化)
- [11. 向量化的更多例子](#11. 向量化的更多例子)
- [12. 向量化logistic回归](#12. 向量化logistic回归)
- [13. 向量化logistic回归的梯度输出](#13. 向量化logistic回归的梯度输出)
- [14. Python中的广播](#14. Python中的广播)
- [15. 关于python_numpy向量的说明](#15. 关于python_numpy向量的说明)
- [16. Jupyter Ipython笔记本的快速指南](#16. Jupyter Ipython笔记本的快速指南)
- [17. logistic损失函数的解释(选修)](#17. logistic损失函数的解释(选修))
1. 二分分类
在神经网络的计算中,通常有一个正向过程,或者叫正向传播步骤,接着会有一个反向步骤,也叫做反向传播步骤。接下来我们将会用logistic回归来阐述这个过程。
下面有一个问题,当我们给神经网络输入一张图片,神经网络需要输出一个结果,1表示图中有猫猫,0表示图中没有猫猫,那么这个过程我们如何实现呢?
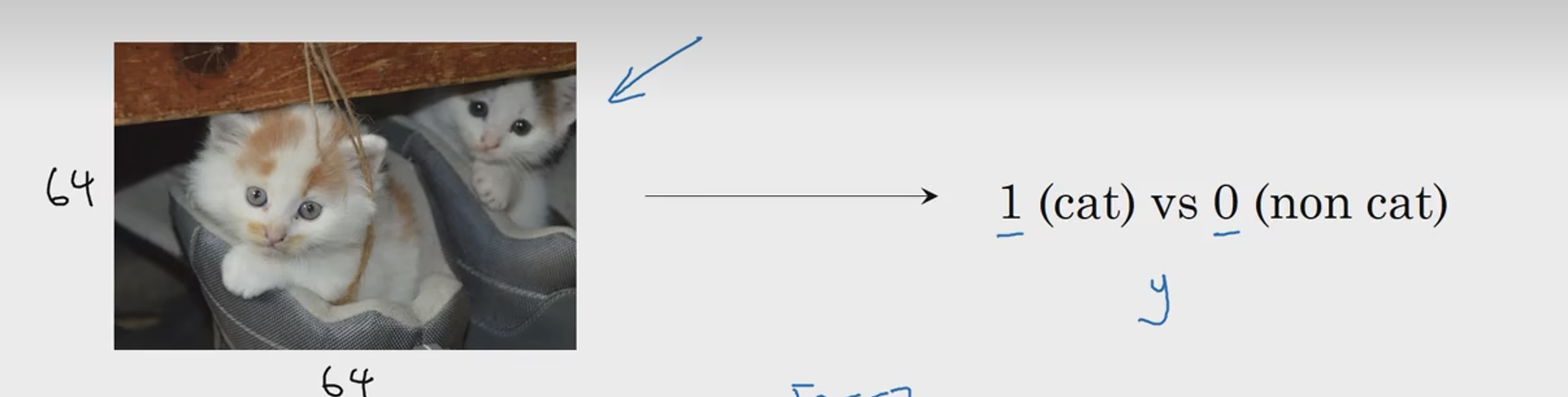
这样的问题我们也可以叫做二分分类问题,下面我们看看如何解决?

首先,对于一张彩色图像,我们可以将其分为三个通道(R、G、B),每个通道由很多个像素点构成,像素点数值的大小表示对应颜色的深浅,最终通过三个通道颜色值的各种组合就可以显示出很多很多种颜色。然后我们将这三个通道中的像素点的值一行一行地收集起来,放入一个列向量X中,那么这个列向量可以看作这个图片的特征向量,其中元素的个数为64x64x3(假设为64x64图像),所以nx = 64x64x3 = 12288,在二分分类问题中,我们的目标是训练出一个分类器,它以图片的特征向量x作为输入,预测输出的结果y是1还是0。

接下来我们符号化一下表示,首先将x和y放在一起,x表示某张图片的特征向量,y表示分类结果,将所有的样本图片和与其对应的分类结果放在一块,即可组成数量为m的训练集,然后将所有x特征向量按列依次放入一个矩阵中即可组成一个X,表示待分类的图片特征数据矩阵,在Python语言中X.shape = (nx,m),分类完成后,结果矩阵Y,表示所有分类结果数据,在Python语言中Y.shape = (1,m)。
2. logistic回归
logistic回归是一个学习算法,用在监督学习问题中,输出y标签是0或1时,这是一个二元分类问题。

在这里,简单来说,就是给了输入的特征向量x,想要得到预测值y帽(在这里类比识别猫的例子我们可将其看成图片中是猫的概率),我们就需要去实现一个线性回归函数y帽 = wTx + b,但是由于概率处于0到1之间,所以我们需要使用一个函数去约束y帽的范围,是的,sigmoid函数就很适合用来约束,因为sigmoid函数当x趋向于正无穷的时候,图像无限贴近于1,当x趋向于负无穷的时候,图像无限趋向于0。所以这个时候回归函数就成了y帽 = σ(wTx + b)。
3. logistic回归损失函数
损失函数 又叫做误差函数 ,可以用来衡量算法的运行情况。我们可以定义损失函数为L(y帽,y) = 1/2(y帽 - y)²,我们通过定义这个损失函数L来衡量你的预测输出值y帽和y的实际值有多接近。这个函数看似合理,但是用这个函数的话,梯度下降法就不太好用 ,在logistic回归中,我们会定义一个不同的损失函数,它起着与误差平方相似的作用。

在这里我们选用这个损失函数L(y帽, y) = - (ylogy帽 + (1-y)log(1-y帽)),为了能更好地理解,为什么它能够起作用,让我们来看两个例子。
当y = 1的时候,L(y帽, y) = - logy帽,这时候如果想要让L尽可能地小,只能让logy帽足够大,所以y帽就要足够大,但是因为y帽是通过sigmoid函数得出的,所以它地范围就在0到1之间,所以y帽子最大只能是1,所以只能让y帽尽可能地接近1。
当y = 0的时候,L(y帽, y) = - log(1 - y帽),这时候如果想要让L尽可能地小,只能让log(1 - y帽)足够大,所以y帽就应该足够小,但是因为y帽是通过sigmoid函数得出的,所以它地范围就在0到1之间,所以y帽子最小只能是0,所以只能让y帽尽可能地接近0。
以上就稍微解释了为什么要用这个作为损失函数。损失函数实在单个训练样本中定义的,它衡量了在单个训练样本上的表现。
下面定义一个成本函数 ,它衡量的是在全体训练样本 上的表现,这个成本函数为J(w, b) = 1/mΣ(求和从1到m)L(y帽, y) = -1/mΣ(求和从1到m)((ylogy帽 + (1-y)log(1-y帽))),所以在训练logistic回归模型的时候,我们要找到合适的参数w和b。
4. 梯度下降法
损失函数是衡量单一训练样例的效果,成本函数用于衡量参数w和b的效果。 我们要得到使得成本函数J(w, b)尽可能小的w和b。
为了找到更好的参数值,我们要做的就是用某初始值初始化w和b,通常用0来进行初始化。
梯度下降法所做的就是从初始点开始,朝最陡的下坡方向走一步。

这张图片阐述了梯度下降法,下面我们从细节方面讨论一下梯度下降法。
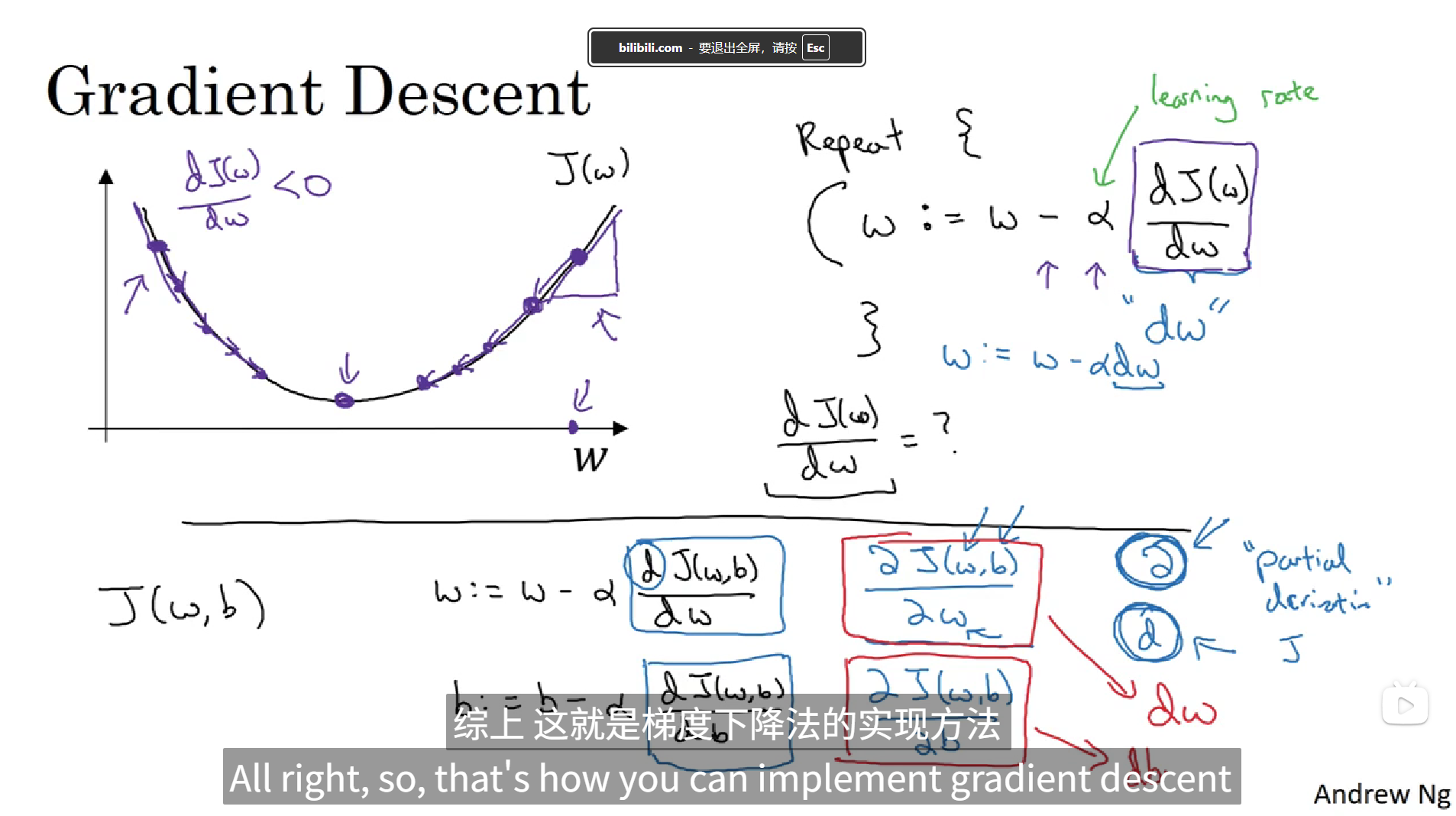
在上面的图中,我们截取了三维坐标的w-J平面来讨论梯度下降法,这里给了一个w的更新公式w := w - α dJ(w)/dw,α被叫做学习率,这个公式的意思就是w就等于w减去α乘以J对w的倒数,然后不断重复迭代这个过程去获取使得J达到最小,也就是使J到达图像最低点的w,以同样的方法也可以用到J对b的过程中,于是导数就变成了偏导数,在这两个自变量w和b的迭代更新计算过程中使用的是J对w的偏导和J对b的偏导,在代码中可以表示为dw和db。
综上,这就是实现梯度下降法的实现方法。
5. 导数


6. 计算图
一个神经网络的计算都是按照前向或反向传播过程来实现的,首先计算出神经网络的输出,紧接着进行一个反向传输操作。
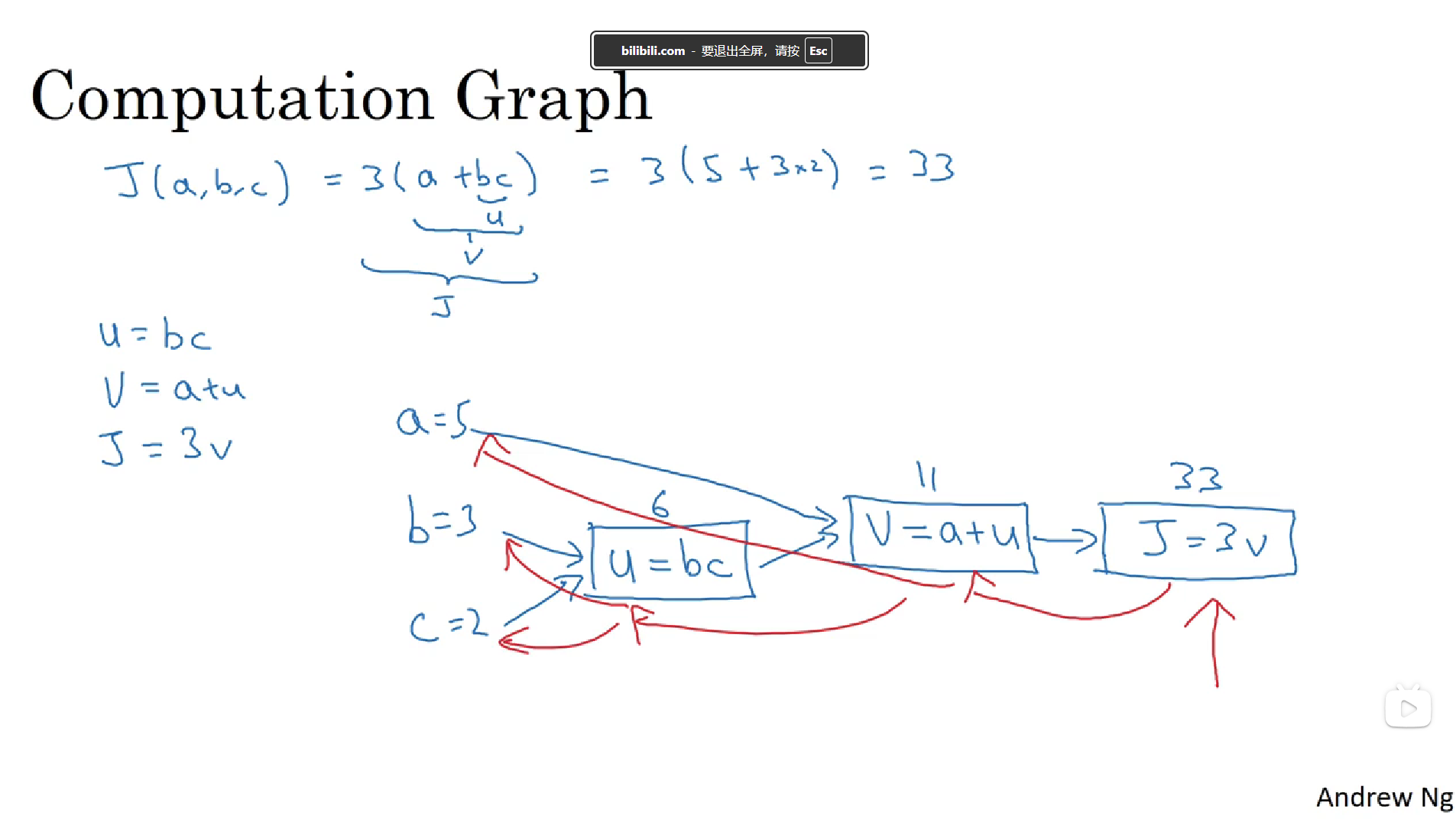
7. 计算图的导数计算


在反向传播算法中的术语 我们看到如果你想计算最后输出的变量的导数,使用你最关心的变量对v的导数,那么我们就做完了一步反向传播。
8. logistic回归中的梯度下降法
下面,我们分析logistic回归中的梯度下降法,我们要通过计算偏导数的方法实现梯度更新。


上面是损失函数L的组成,要想计算损失函数L的导数,我们要先计算dL/da,根据求导公式我们可以算出"da" = dL/da = -y/a + (1-y)/(1-a),这是从后向前传导的第一步过程,第二部过程就是计算dz = dL/dz = dL/dz = dL/da * da/dz = ( -y/a + (1-y)/(1-a)) * (a(1-a)) = a - y,这一步用的是链式求导法则,同理偏L/偏w1 = "dw1" = x1 * dz,还有"dw2" = x2 * dz、"db = dz",最后再进行参数的更新,即w1 := w1 - αdw1,w2 := w2 - αdw2,b := b - αdb。以上就是单个样本的logstic回归的梯度下降法。
9. m个样本的梯度下降
上面我们计算完一个样本的梯度下降,那么m个样本的梯度下降也是换汤不换药的,首先我们回忆成本函数的写法,把他们写成求和的形式为J(w,b) = 1/mΣ(从1到m)L(a(i),y(i)) ,a(i) = y帽(i) = σ(z(i)) = σ(wTx + b) ,然后我们要分别对每个参数dw1(i),dw2(i),db(i)求偏导,在这里只不过把求偏导的过程放到了求和公式里面,除了这个其他求解过程是不变的。

接下来我们用一张图来说明m个样本进行logistic回归梯度下降的全过程,这里分析用的是伪代码。

这里用的是双重for循环 进行梯度下降的,可以简单理解成外层for循环用来循环m个样本,内层for循环用来更新每个需要更新的参数。但是这种算法比较传统且低效,计算成本高,后面我们会介绍另一种计算思路---向量化,用这种方法计算会大幅度降低计算成本且不会显式使用这么多for循环,让代码看起来更加简洁美观。
10. 向量化
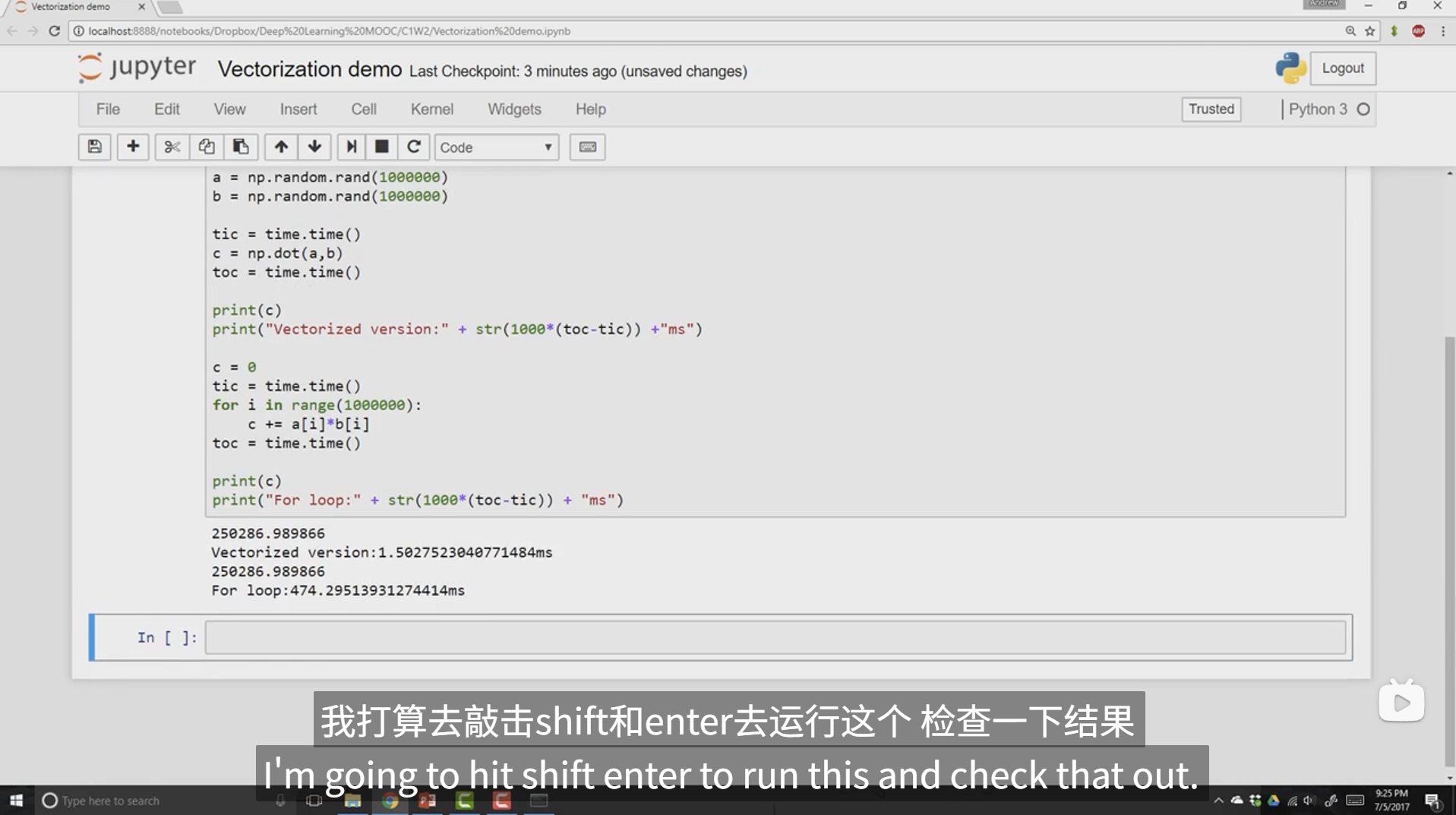
其实这里的向量化用我的理解来讲就是把每个需要被循环处理的数据合并为一个大的列向量,然后将大向量进行相应的矩阵运算,这样就省去了循环的步骤,直接一步到位算出结果。

以下通过代码对比了进行1000000次矩阵运算,利用for循环和利用向量化计算在速度上的差异,根据结果可以发现,利用循环所消耗的时间是利用向量化消耗时间的300倍左右,由此可见向量化的优势所在。
11. 向量化的更多例子
以下是计算指数,对数,绝对值和最大值的向量化的例子。

以下对m个样本的梯度下降过程通过向量化进行了简化,主要是把内层特征参数的计算过程进行了向量化,这样就能省去内层循环,简化代码并且提高计算速度。

12. 向量化logistic回归

13. 向量化logistic回归的梯度输出


14. Python中的广播


15. 关于python_numpy向量的说明
这里主要是给一个建议,如果进行dot矩阵运算前,最好对待计算向量进行reshape,指定好他是多少维度的矩阵以后再进行运算,这样可以避免因为形式错误而出现一些问题。

16. Jupyter Ipython笔记本的快速指南
略。
17. logistic损失函数的解释(选修)

