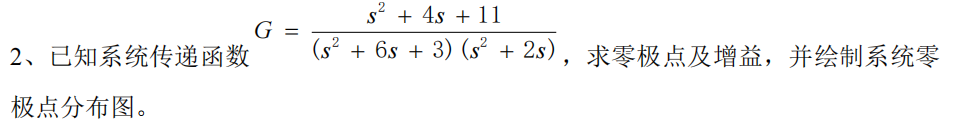Matlab求传递函数的零极点及增益并绘制零极点图 2

题目：

代码：

Matlab 复制代码

clc;clear all;close all;

num=[1 4 11];%定义传递函数的分子的系数s^2+4s+11
den=conv([1 6 3],[1 2 0]);%conv()函数是两个多项式的乘积，
                          % 即(s^2+6s+3)*(s^2+2s)
sys=tf(num,den);%tf()函数创建传递函数
[z,p,k]=tf2zp(num,den);%tf2zp()函数用于求系统的零极点和增益
disp('Zero:');%零点
disp(z);
disp('Poles:');%极点
disp(p);
disp('Gain:');%增益
disp(k);

figure%创建一张新的图
pzmap(sys);%pzmap()用于绘制图
title('Pole_Zero Map');

%找到零极点
[z,p,~]=tf2zp(num,den);
%标注极点
for i=1:length(z)
    text(real(z(i)),imag(z(i)),['' num2str(z(i),'%.2f')],'Color','blue');
end
%标注极点
for i=1:length(p)
    text(real(p(i)),imag(p(i)),['' num2str(p(i),'%.2f')],'Color','red');
end

实验结果：

1. 清空环境与命令窗口

Matlab 复制代码

clc;
clear all;
close all;

功能：

clc：清空命令窗口，让屏幕更整洁。
clear all：清除工作区所有变量，避免之前的变量对当前代码产生干扰。
close all：关闭所有打开的图形窗口，防止残留的图影响后续结果显示。

2. 定义传递函数的分子和分母系数

Matlab 复制代码

num=[1 4 11];%定义传递函数的分子的系数s^2+4s+11
den=conv([1 6 3],[1 2 0]);%conv()函数是两个多项式的乘积，即(s^2+6s+3)*(s^2+2s)

功能：

num ：分子系数向量，对应多项式 \(s^2 + 4s + 11\)。
- 向量中的元素按降幂排列，即 [s²的系数, s的系数, 常数项]。
den ：分母系数向量，通过 conv 函数计算两个多项式的乘积。

conv 函数：

用于计算两个向量的卷积，在多项式运算中相当于多项式乘法。
语法：conv(a, b)，其中 a 和 b 是两个多项式的系数向量（降幂排列）。

3. 创建传递函数模型

Matlab 复制代码

sys=tf(num,den);%tf()函数创建传递函数

功能：

tf(num, den) 是 MATLAB 控制工具箱（Control System Toolbox）中的核心函数，用于创建传递函数模型。
sys 是一个 tf 类型的对象，包含了传递函数的所有信息（分子、分母、采样时间等），后续可用于分析（如求零极点、绘制响应曲线等）。

用法示例：

Matlab 复制代码

num = [1 2];    % 分子：s + 2
den = [1 3 2];  % 分母：s² + 3s + 2
sys = tf(num, den);  % 传递函数：(s+2)/(s²+3s+2)

4. 求系统的零极点和增益

Matlab 复制代码

[z,p,k]=tf2zp(num,den);%tf2zp()函数用于求系统的零极点和增益

功能：

tf2zp(num, den) 用于将传递函数从多项式形式 转换为零极点形式。

参数说明：

输入：num（分子系数向量）、den（分母系数向量）。
输出：
- z：零点向量（每个元素是一个零点）。
- p：极点向量（每个元素是一个极点）。
- k：增益（标量）。

5. 显示零极点和增益

Matlab 复制代码

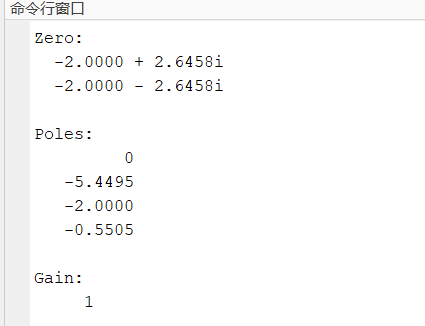
disp('Zero:');%零点
disp(z);
disp('Poles:');%极点
disp(p);
disp('Gain:');%增益
disp(k);

功能：

disp('字符串')：在命令窗口显示提示信息。
disp(z)、disp(p)、disp(k)：分别显示零点、极点和增益的具体数值。

示例输出：

Matlab 复制代码

Zero:
   -2.0000 + 2.6458i
   -2.0000 - 2.6458i

Poles:
    0.0000
   -2.0000
   -3.0000 + 2.4495i
   -3.0000 - 2.4495i

Gain:
     1

6. 绘制零极点图

Matlab 复制代码

figure%创建一张新的图
pzmap(sys);%pzmap()用于绘制图
title('Pole_Zero Map');

功能：

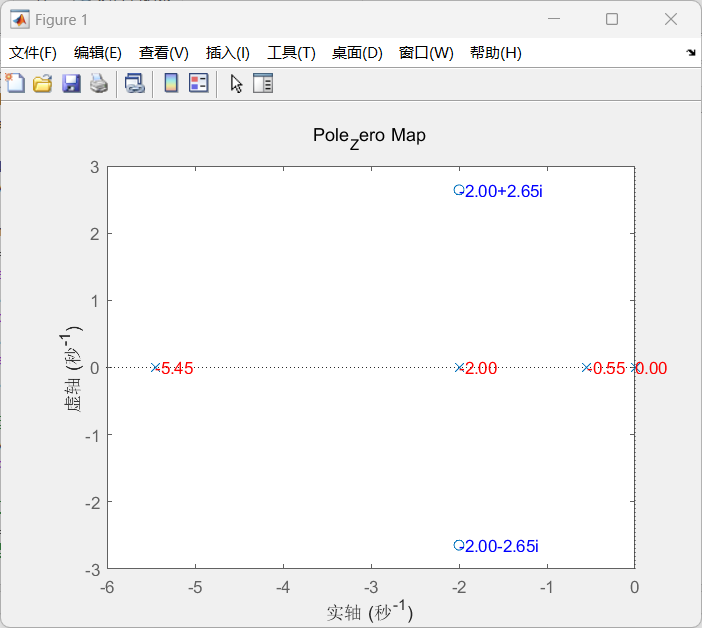
figure：创建一个新的图形窗口，用于绘制后续图形。
pzmap(sys)：绘制系统的零极点图 （Pole-Zero Map）。
- 零极点图是在复平面 （实轴为横坐标，虚轴为纵坐标）上绘制的：
  - 零点用 空心圆（○）表示。
  - 极点用叉号（×）表示。
- 该图用于直观分析系统的稳定性（极点是否全部在左半平面）、动态性能（零极点的位置分布）等。
title('Pole_Zero Map')：为图形添加标题。

7. 标注零极点的数值

Matlab 复制代码

%找到零极点
[z,p,~]=tf2zp(num,den);
%标注极点
for i=1:length(z)
    text(real(z(i)),imag(z(i)),['' num2str(z(i),'%.2f')],'Color','blue');
end
%标注极点
for i=1:length(p)
    text(real(p(i)),imag(p(i)),['' num2str(p(i),'%.2f')],'Color','red');
end

功能：

再次调用 tf2zp(num, den) 获取零极点（~ 表示忽略增益 k，因为之前已获取）。
通过 for 循环遍历每个零点和极点，并用 text 函数在零极点图上标注其数值。

关键函数说明：

length(z)：获取零点向量 z 的长度（即零点的个数）。
real(z(i))：获取第 i 个零点的实部（作为标注的横坐标）。
imag(z(i))：获取第 i 个零点的虚部（作为标注的纵坐标）。
num2str(z(i),'%.2f')：将复数零点 z(i) 转换为字符串，保留 2 位小数。
text(x, y, '字符串', 'Color', '颜色')：在图形的 (x, y) 位置添加文本标注，颜色设为蓝色（零点）或红色（极点）。

效果：

零极点图上每个零点和极点的旁边会显示其具体数值（如 -2.00 + 2.65i），方便精确读取。

总结

这段代码的核心功能是：

定义传递函数的分子和分母（通过系数向量和多项式乘法）。
创建传递函数模型并转换为零极点形式。
显示零极点和增益的数值。
绘制零极点图并标注具体数值，用于系统分析。