MATLAB基于麻雀搜索算法的栅格地图路径规划

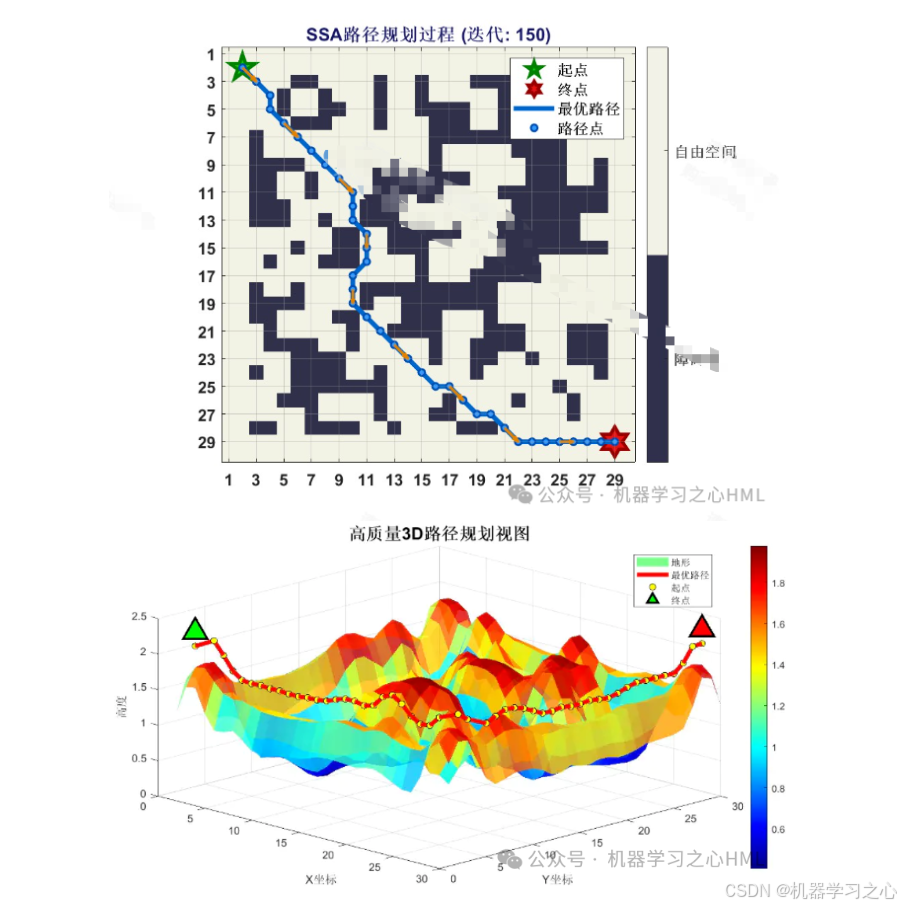
1. 算法原理

麻雀搜索算法是一种新型的群智能优化算法，模拟麻雀的觅食和反捕食行为：

发现者：引领群体寻找食物源
加入者：跟随发现者寻找食物
警戒者：侦查危险并发出警报

2. MATLAB实现代码

主程序 `SSA_PathPlanning.m`

matlab 复制代码

% 基于麻雀搜索算法的栅格地图路径规划
clear; clc; close all;

%% 参数设置
numSparrows = 30;      % 麻雀数量
maxIter = 100;         % 最大迭代次数
dim = 2;               % 每个路径点的维度(x,y)
numPoints = 10;        % 路径点数量（不含起点终点）
PD = 0.7;              % 发现者比例
SD = 0.2;              % 警戒者比例
ST = 0.8;              % 安全阈值

%% 创建栅格地图
mapSize = 20;          % 地图大小
map = createMap(mapSize);  % 创建随机栅格地图
% 或者使用固定地图
% map = [0 0 0 0 0 0 0 0 0 0;
%        0 1 1 0 0 0 1 1 0 0;
%        0 0 0 0 1 0 0 0 0 0;
%        0 1 0 0 1 0 1 1 0 0;
%        0 1 0 0 1 0 0 1 0 0;
%        0 0 0 0 0 0 0 0 0 0];

%% 设置起点和终点
startPos = [1, 1];     % 起点坐标
goalPos = [mapSize, mapSize];  % 终点坐标

%% 显示地图
figure(1);
hold on;
imagesc(1:mapSize, 1:mapSize, map);
colormap([1 1 1; 0 0 0]);  % 0=白色(可行), 1=黑色(障碍)
plot(startPos(1), startPos(2), 'go', 'MarkerSize', 10, 'LineWidth', 3);
plot(goalPos(1), goalPos(2), 'ro', 'MarkerSize', 10, 'LineWidth', 3);
xlabel('X'); ylabel('Y');
title('栅格地图路径规划');
grid on;
axis equal;

%% 初始化麻雀种群
sparrows = zeros(numSparrows, numPoints*dim);
fitness = zeros(numSparrows, 1);

% 随机初始化路径点
for i = 1:numSparrows
    path = initializePath(startPos, goalPos, numPoints, mapSize, map);
    sparrows(i, :) = path(:)';
    fitness(i) = calculateFitness(path, startPos, goalPos, map);
end

%% SSA主循环
bestFitness = inf;
bestPath = [];
convergenceCurve = zeros(maxIter, 1);

for iter = 1:maxIter
    % 排序，找到最佳和最差适应度
    [sortedFitness, sortedIdx] = sort(fitness);
    bestIdx = sortedIdx(1);
    worstIdx = sortedIdx(end);
    
    % 更新全局最优
    if sortedFitness(1) < bestFitness
        bestFitness = sortedFitness(1);
        bestPath = reshape(sparrows(bestIdx, :), numPoints, dim);
    end
    
    % 计算发现者、加入者、警戒者的数量
    numDiscoverers = round(numSparrows * PD);
    numWatchers = round(numSparrows * SD);
    numFollowers = numSparrows - numDiscoverers - numWatchers;
    
    %% 更新发现者位置
    for i = 1:numDiscoverers
        R2 = rand();  % 预警值
        if R2 < ST
            % 安全，正常搜索
            sparrows(sortedIdx(i), :) = sparrows(sortedIdx(i), :) .* ...
                exp(-i / (rand() * maxIter));
        else
            % 危险，飞向安全区域
            sparrows(sortedIdx(i), :) = sparrows(sortedIdx(i), :) + ...
                randn(1, numPoints*dim) .* ones(1, numPoints*dim);
        end
    end
    
    %% 更新加入者位置
    for i = numDiscoverers+1:numDiscoverers+numFollowers
        if i > numSparrows/2
            % 饥饿的加入者
            sparrows(sortedIdx(i), :) = randn(1, numPoints*dim) .* ...
                exp((sparrows(worstIdx, :) - sparrows(sortedIdx(i), :)) / i^2);
        else
            % 跟随发现者
            A = floor(rand(1, numPoints*dim) * 2) * 2 - 1;
            sparrows(sortedIdx(i), :) = sparrows(bestIdx, :) + ...
                abs(sparrows(sortedIdx(i), :) - sparrows(bestIdx, :)) * ...
                A' * (A * A')^(-1);
        end
    end
    
    %% 更新警戒者位置
    for i = numSparrows-numWatchers+1:numSparrows
        f_i = fitness(sortedIdx(i));
        f_g = bestFitness;
        f_w = fitness(worstIdx);
        
        if f_i > f_g
            % 靠近最佳位置
            sparrows(sortedIdx(i), :) = sparrows(bestIdx, :) + ...
                randn(1, numPoints*dim) .* abs(sparrows(sortedIdx(i), :) - ...
                sparrows(bestIdx, :));
        elseif f_i == f_g
            % 保持当前位置
            c = randn(1, numPoints*dim);
            sparrows(sortedIdx(i), :) = sparrows(sortedIdx(i), :) + ...
                c .* (abs(sparrows(sortedIdx(i), :) - sparrows(worstIdx, :)) / ...
                (f_i - f_w + eps));
        end
    end
    
    %% 边界处理
    for i = 1:numSparrows
        % 确保路径点在范围内
        path = reshape(sparrows(i, :), numPoints, dim);
        for j = 1:numPoints
            path(j, 1) = max(min(path(j, 1), mapSize), 1);
            path(j, 2) = max(min(path(j, 2), mapSize), 1);
        end
        sparrows(i, :) = path(:)';
        
        % 重新计算适应度
        fitness(i) = calculateFitness(path, startPos, goalPos, map);
    end
    
    convergenceCurve(iter) = bestFitness;
    
    %% 显示当前最优路径
    if mod(iter, 10) == 0
        fprintf('迭代 %d, 最佳适应度: %.4f\n', iter, bestFitness);
        
        figure(1);
        hold on;
        plotPath(bestPath, startPos, goalPos, 'b-');
        title(sprintf('迭代 %d, 适应度: %.4f', iter, bestFitness));
        drawnow;
    end
end

%% 显示最终结果
figure(1);
hold on;
finalPath = [startPos; bestPath; goalPos];
plot(finalPath(:,1), finalPath(:,2), 'r-', 'LineWidth', 2);
plot(bestPath(:,1), bestPath(:,2), 'b*');
title(sprintf('最终路径 (适应度: %.4f)', bestFitness));

figure(2);
plot(convergenceCurve, 'b-', 'LineWidth', 2);
xlabel('迭代次数');
ylabel('最佳适应度');
title('收敛曲线');
grid on;

%% 平滑路径
smoothedPath = smoothPath(finalPath, map);
figure(3);
imagesc(1:mapSize, 1:mapSize, map);
colormap([1 1 1; 0 0 0]);
hold on;
plot(startPos(1), startPos(2), 'go', 'MarkerSize', 10, 'LineWidth', 3);
plot(goalPos(1), goalPos(2), 'ro', 'MarkerSize', 10, 'LineWidth', 3);
plot(smoothedPath(:,1), smoothedPath(:,2), 'm-', 'LineWidth', 2);
title('平滑后路径');
grid on; axis equal;

辅助函数 `createMap.m`

matlab 复制代码

function map = createMap(mapSize)
% 创建随机栅格地图
% mapSize: 地图尺寸
% 返回值: 二值地图 (0=可行, 1=障碍)

map = zeros(mapSize);
% 随机生成障碍物
obstacleRatio = 0.2;  % 障碍物比例
numObstacles = round(mapSize * mapSize * obstacleRatio);

for i = 1:numObstacles
    x = randi([1, mapSize]);
    y = randi([1, mapSize]);
    % 避免起点和终点被设为障碍
    if ~((x == 1 && y == 1) || (x == mapSize && y == mapSize))
        map(y, x) = 1;
    end
end

% 添加一些连续的障碍物
for i = 1:mapSize
    if rand() < 0.3
        startX = randi([1, mapSize-5]);
        length = randi([3, 6]);
        for j = 0:length
            if startX + j <= mapSize
                map(i, startX+j) = 1;
            end
        end
    end
end
end

路径初始化函数 `initializePath.m`

matlab 复制代码

function path = initializePath(startPos, goalPos, numPoints, mapSize, map)
% 初始化路径
% numPoints: 中间路径点数量

path = zeros(numPoints, 2);

for i = 1:numPoints
    % 在起点和终点之间均匀分布路径点
    ratio = i / (numPoints + 1);
    x = startPos(1) + ratio * (goalPos(1) - startPos(1));
    y = startPos(2) + ratio * (goalPos(2) - startPos(2));
    
    % 添加随机扰动
    x = x + randn() * 2;
    y = y + randn() * 2;
    
    % 确保在边界内
    x = max(min(x, mapSize), 1);
    y = max(min(y, mapSize), 1);
    
    % 避开障碍物
    while map(round(y), round(x)) == 1
        x = x + randn();
        y = y + randn();
        x = max(min(x, mapSize), 1);
        y = max(min(y, mapSize), 1);
    end
    
    path(i, :) = [x, y];
end
end

适应度计算函数 `calculateFitness.m`

matlab 复制代码

function fitness = calculateFitness(path, startPos, goalPos, map)
% 计算路径适应度
% 适应度 = 路径长度 + 障碍物惩罚

% 完整路径
fullPath = [startPos; path; goalPos];

% 计算路径长度
pathLength = 0;
for i = 1:size(fullPath, 1)-1
    dist = norm(fullPath(i, :) - fullPath(i+1, :));
    pathLength = pathLength + dist;
end

% 检查碰撞惩罚
collisionPenalty = 0;
collisionWeight = 100;  % 碰撞惩罚权重

for i = 1:size(fullPath, 1)
    x = round(fullPath(i, 1));
    y = round(fullPath(i, 2));
    
    % 边界检查
    if x < 1 || x > size(map, 2) || y < 1 || y > size(map, 1)
        collisionPenalty = collisionPenalty + collisionWeight;
        continue;
    end
    
    % 障碍物检查
    if map(y, x) == 1
        collisionPenalty = collisionPenalty + collisionWeight;
    end
end

% 检查路径段是否穿过障碍物
segmentPenalty = 0;
for i = 1:size(fullPath, 1)-1
    p1 = fullPath(i, :);
    p2 = fullPath(i+1, :);
    
    % 采样路径段上的点
    numSamples = 10;
    for t = 0:1/numSamples:1
        p = p1 + t * (p2 - p1);
        x = round(p(1));
        y = round(p(2));
        
        if x >= 1 && x <= size(map, 2) && y >= 1 && y <= size(map, 1)
            if map(y, x) == 1
                segmentPenalty = segmentPenalty + collisionWeight/numSamples;
            end
        end
    end
end

% 总适应度
fitness = pathLength + collisionPenalty + segmentPenalty;
end

路径平滑函数 `smoothPath.m`

matlab 复制代码

function smoothedPath = smoothPath(path, map)
% 平滑路径
% 使用简单的B样条平滑

n = size(path, 1);
if n < 3
    smoothedPath = path;
    return;
end

% B样条平滑
t = linspace(0, 1, n);
tt = linspace(0, 1, n*3);

% 使用三次样条插值
smoothedPath(:,1) = spline(t, path(:,1), tt);
smoothedPath(:,2) = spline(t, path(:,2), tt);

% 确保路径避开障碍物
for i = 1:size(smoothedPath, 1)
    x = round(smoothedPath(i, 1));
    y = round(smoothedPath(i, 2));
    
    if x >= 1 && x <= size(map, 2) && y >= 1 && y <= size(map, 1)
        if map(y, x) == 1
            % 如果碰到障碍物，调整点
            % 寻找最近的可行点
            found = false;
            for r = 1:5
                for angle = 0:pi/8:2*pi
                    newX = round(x + r * cos(angle));
                    newY = round(y + r * sin(angle));
                    if newX >= 1 && newX <= size(map, 2) && ...
                       newY >= 1 && newY <= size(map, 1) && ...
                       map(newY, newX) == 0
                        smoothedPath(i, :) = [newX, newY];
                        found = true;
                        break;
                    end
                end
                if found, break; end
            end
        end
    end
end
end

路径绘制函数 `plotPath.m`

matlab 复制代码

function plotPath(path, startPos, goalPos, style)
% 绘制路径
fullPath = [startPos; path; goalPos];
plot(fullPath(:,1), fullPath(:,2), style, 'LineWidth', 1.5);
plot(path(:,1), path(:,2), 'b*');
plot(startPos(1), startPos(2), 'go', 'MarkerSize', 10, 'LineWidth', 3);
plot(goalPos(1), goalPos(2), 'ro', 'MarkerSize', 10, 'LineWidth', 3);
end

3. 算法特点

快速收敛：SSA算法具有较快的收敛速度
全局搜索：通过发现者机制进行全局探索
局部优化：加入者和警戒者机制进行局部优化
避障能力：适应度函数包含障碍物惩罚项

4. 参数调优建议

matlab 复制代码

% 关键参数调优建议
% 1. 麻雀数量：20-50，复杂环境可以适当增加
% 2. PD（发现者比例）：0.6-0.8
% 3. ST（安全阈值）：0.6-0.9
% 4. 迭代次数：50-200，根据地图复杂度调整

MATLAB基于麻雀搜索算法的栅格地图路径规划

1. 算法原理

2. MATLAB实现代码

主程序 SSA_PathPlanning.m

辅助函数 createMap.m

路径初始化函数 initializePath.m

适应度计算函数 calculateFitness.m

路径平滑函数 smoothPath.m

路径绘制函数 plotPath.m

3. 算法特点

4. 参数调优建议

主程序 `SSA_PathPlanning.m`

辅助函数 `createMap.m`

路径初始化函数 `initializePath.m`

适应度计算函数 `calculateFitness.m`

路径平滑函数 `smoothPath.m`

路径绘制函数 `plotPath.m`