Opencv(十六) : 图像边缘检测

文章目录

- 思维导图
- 一、前言
- 二、最优边缘检测准则
- - [1. 最优检测准则](#1. 最优检测准则)
  - [2. 最优定位准则](#2. 最优定位准则)
  - [3. 检测点与边缘点](#3. 检测点与边缘点)
- 三、核心算法步骤详解
- - [1. 高斯滤波](#1. 高斯滤波)
  - - [1.1 原理与必要性](#1.1 原理与必要性)
    - [1.2 高斯核的定义与计算](#1.2 高斯核的定义与计算)
    - [1.3 卷积运算过程](#1.3 卷积运算过程)
    - [1.4 难点标注](#1.4 难点标注)
  - [2. 计算图像梯度与方向](#2. 计算图像梯度与方向)
  - - [2.1 梯度的物理意义](#2.1 梯度的物理意义)
    - [2.2 Sobel算子：梯度计算的工具](#2.2 Sobel算子：梯度计算的工具)
    - [2.3 梯度幅值与方向计算](#2.3 梯度幅值与方向计算)
    - [2.4 边缘方向分类](#2.4 边缘方向分类)
    - [2.5 难点标注](#2.5 难点标注)
  - [3. 非极大值抑制](#3. 非极大值抑制)
  - - [3.1 原理与目标](#3.1 原理与目标)
    - [3.2 实现步骤](#3.2 实现步骤)
    - [3.3 插值处理](#3.3 插值处理)
    - [3.4 难点标注](#3.4 难点标注)
  - [4. 双阈值筛选](#4. 双阈值筛选)
  - - [4.1 原理与必要性](#4.1 原理与必要性)
    - [4.2 阈值设定原则](#4.2 阈值设定原则)
    - [4.3 筛选规则](#4.3 筛选规则)
    - [4.4 滞后边界跟踪](#4.4 滞后边界跟踪)
    - [4.5 难点标注](#4.5 难点标注)
  - [5. 边缘输出](#5. 边缘输出)
- [四、 Sobel算子](#四、 Sobel算子)
- - [1. Sobel算子的定义与优势](#1. Sobel算子的定义与优势)
  - [2. Sobel算子的扩展](#2. Sobel算子的扩展)
  - [3. Sobel算子的局限性](#3. Sobel算子的局限性)
- 五、算法参数选择与优化建议
- - [1. 高斯核参数（ σ \sigma σ 与核大小）](#1. 高斯核参数（ σ \sigma σ 与核大小）)
  - [2. 双阈值（ T h i g h T_{high} Thigh 与 T l o w T_{low} Tlow）](#2. 双阈值（ T h i g h T_{high} Thigh 与 T l o w T_{low} Tlow）)
  - [3. 边缘连通性判断](#3. 边缘连通性判断)
  - [4. 预处理与后处理优化](#4. 预处理与后处理优化)
- 六、代码示例
- 七、常见问题与解决方案
- 八、算法应用场景与局限性
- - [1. 典型应用场景](#1. 典型应用场景)
  - - [1.1 工业质检](#1.1 工业质检)
    - [1.2 医学影像](#1.2 医学影像)
    - [1.3 自动驾驶](#1.3 自动驾驶)
    - [1.4 图像配准](#1.4 图像配准)
  - [2. 局限性](#2. 局限性)
- 九、总结与展望

思维导图

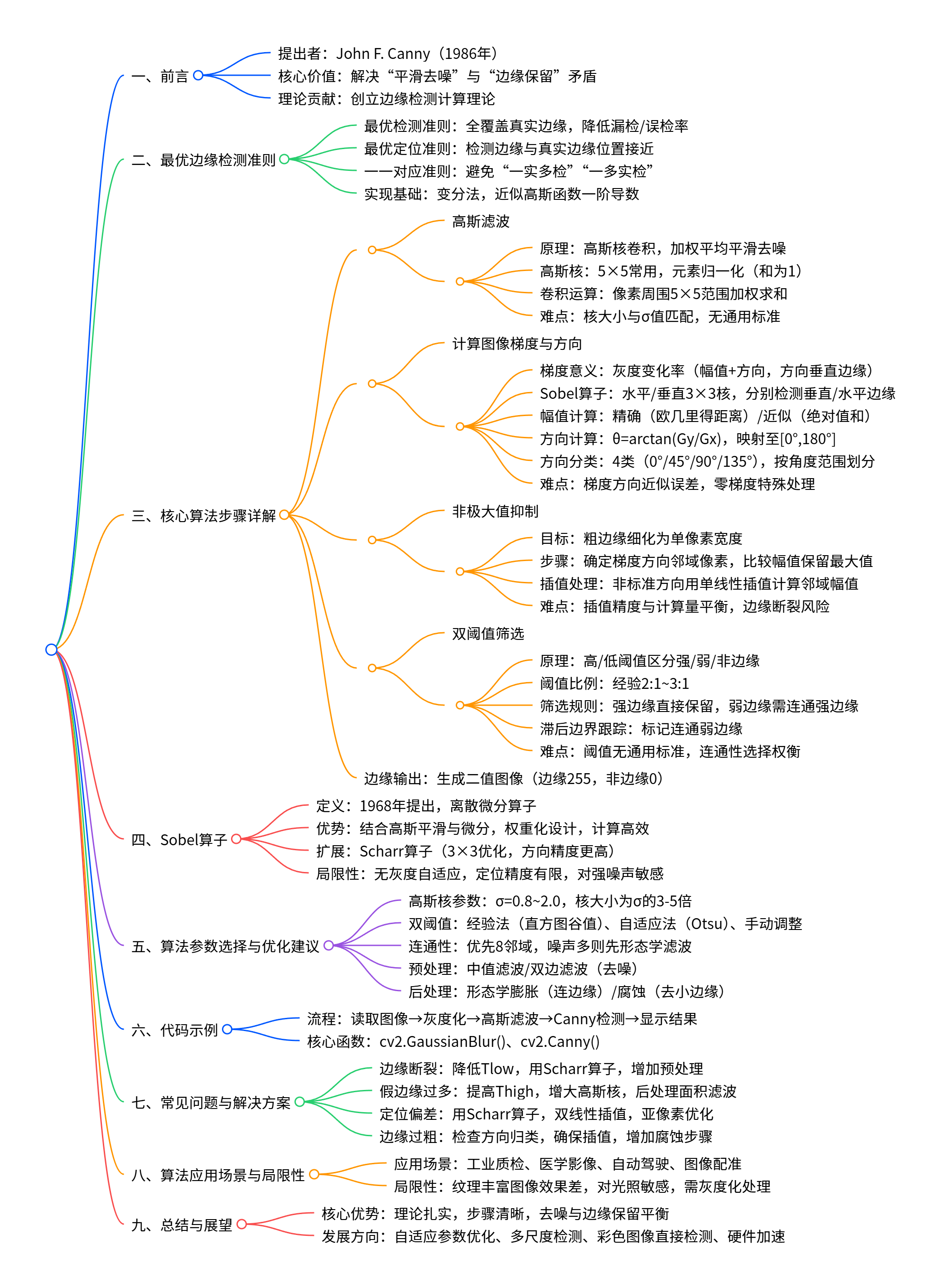
一、前言

Canny边缘检测算法是由John F. Canny于1986年提出的一种基于图像梯度计算的多级边缘检测算法，至今仍是计算机视觉领域应用最广泛的边缘检测方法之一。其核心价值在于解决了"平滑去噪"与"边缘保留"这对矛盾------通过引入高斯函数的一阶导数，在抑制噪声的同时，最大程度保留图像边缘的细节信息，还创立了边缘检测计算理论，为后续边缘检测技术的发展奠定了理论基础。

二、最优边缘检测准则

Canny算法的核心优势源于其对"最优边缘检测"的定义与实现，具体包含三大准则，这也是理解算法设计逻辑的关键：

1. 最优检测准则

算法需尽可能多地标识出图像中的实际边缘，同时将漏检真实边缘的概率和误检非边缘（如噪声点）的概率降至最低。这一准则直接决定了算法的"完整性"------既要覆盖所有真实边缘，又要避免将噪声误判为边缘。例如，在工业质检场景中，若漏检零件表面的裂纹边缘，可能导致产品质量问题；若将表面污渍误判为裂纹，则会造成误检成本增加。

2. 最优定位准则

检测到的边缘点位置需与实际边缘点位置尽可能接近，即由噪声引起的边缘偏离真实位置的程度最小。该准则保障了边缘检测的"精度"。以医学影像中的肿瘤边缘检测为例，若检测到的边缘与肿瘤实际边缘偏差较大，会直接影响医生对肿瘤大小、形状的判断，进而影响诊疗方案制定。

3. 检测点与边缘点

算法检测到的边缘点与图像中的实际边缘点需形成一一对应关系，避免出现"一实多检"（一个真实边缘对应多个检测点）或"一多实检"（多个真实边缘对应一个检测点）的情况。这一准则确保了边缘的"连续性"与"唯一性"，例如在交通场景中的车道线检测，若车道线边缘被检测为多条离散线段，会导致车道跟踪算法失效。

为满足上述准则，Canny采用变分法（一种寻找优化特定功能函数的数学方法），通过四个指数函数项近似实现最优检测，最终发现该最优检测过程与高斯函数的一阶导数高度吻合，这也成为后续算法步骤设计的理论依据。

三、核心算法步骤详解

Canny边缘检测算法通过5个紧密衔接的步骤实现，每个步骤均针对上述最优准则设计，环环相扣，共同完成从原始图像到边缘图像的转换。

1. 高斯滤波

1.1 原理与必要性

边缘检测本质是对图像灰度变化的捕捉，属于"锐化操作"，但噪声会导致图像灰度出现无规律波动，干扰边缘判断。高斯滤波通过对原始图像与高斯核进行卷积运算，实现"平滑去噪"------将像素点周围的灰度值按高斯分布加权平均，距离越近的像素权重越大，从而在保留边缘趋势的同时，抑制孤立噪声点。

1.2 高斯核的定义与计算

高斯核（Gaussian Kernel）是一个对称的矩阵，其元素值由高斯函数计算得出，公式如下：
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} G(x,y)=2πσ21e−2σ2x2+y2

其中， σ \sigma σ 为高斯函数的标准差，决定了滤波的平滑程度：

σ \sigma σ 越小：高斯核的权重集中在中心像素，平滑效果弱，能保留更多细节，但去噪能力差；
σ \sigma σ 越大：权重分布越分散，平滑效果强，去噪能力好，但会模糊边缘细节。

在实际应用中，常用的是5×5高斯核（兼顾去噪效果与边缘保留），其元素值已归一化（所有元素和为1，避免滤波后图像整体亮度变化），具体形式如下：
k e r n e l = 1 256 [ 1 4 6 4 1 4 16 24 16 4 6 24 36 24 6 4 16 24 16 4 1 4 6 4 1 ] kernel =\frac{1}{256}\left[\begin{array}{ccccc}1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & 36 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1\end{array}\right] kernel=2561 1464141624164624362464162416414641

分母256是所有元素的和（1+4+6+4+1+4+16+...+1=256），确保卷积后像素值仍在0-255范围内。

1.3 卷积运算过程

假设原始图像为 I I I，高斯核为 K K K，滤波后的图像为 I ′ I' I′，则卷积运算公式为：
I ′ ( x , y ) = ∑ i = − 2 2 ∑ j = − 2 2 K ( i + 2 , j + 2 ) × I ( x + i , y + j ) I'(x,y)=\sum_{i=-2}^{2}\sum_{j=-2}^{2} K(i+2,j+2) \times I(x+i,y+j) I′(x,y)=i=−2∑2j=−2∑2K(i+2,j+2)×I(x+i,y+j)

即对于图像中每个像素 ( x , y ) (x,y) (x,y)，取其周围5×5范围内的像素与高斯核对应元素相乘，再求和，结果作为滤波后该像素的灰度值。

1.4 难点标注

高斯核大小选择：核尺寸过小（如3×3）去噪不充分，过大（如7×7）会过度模糊边缘；需根据图像噪声强度调整，无通用标准，需通过实验验证。
σ \sigma σ 值设定： σ \sigma σ 需与核大小匹配，例如5×5核对应的 σ \sigma σ 通常为1.4，若 σ \sigma σ 过大，核边缘元素权重过小，相当于"有效核大小"减小，浪费计算资源。

2. 计算图像梯度与方向

2.1 梯度的物理意义

图像梯度反映了灰度值的变化率，变化率越大，说明该位置越可能是边缘。梯度是一个矢量，包含梯度幅值 （变化率大小）和梯度方向（变化率最大的方向）------梯度方向始终垂直于边缘方向，这是后续步骤的核心依据。

2.2 Sobel算子：梯度计算的工具

Canny算法采用Sobel算子 计算梯度，该算子是一种离散微分算子，结合了高斯平滑与微分求导，抗噪声能力强，且能提供较精确的边缘方向信息。Sobel算子包含两个3×3核，分别用于计算水平方向（ G x G_x Gx）和垂直方向（ G y G_y Gy）的梯度：

水平方向Sobel核（检测垂直边缘）：
s o b e l ( 水平方向 ) = [ − 1 0 1 − 2 0 2 − 1 0 1 ] sobel(水平方向 )=\left[\begin{array}{ccc}-1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1\end{array}\right] sobel(水平方向)= −1−2−1000121
原理：通过左右像素的灰度差捕捉垂直方向的灰度变化（垂直边缘是水平方向的灰度突变）。
垂直方向Sobel核（检测水平边缘）：
s o b e l ( 垂直方向 ) = [ − 1 − 2 − 1 0 0 0 1 2 1 ] sobel(垂直方向 )=\left[\begin{array}{ccc}-1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1\end{array}\right] sobel(垂直方向)= −101−202−101
原理：通过上下像素的灰度差捕捉水平方向的灰度变化（水平边缘是垂直方向的灰度突变）。

2.3 梯度幅值与方向计算

梯度幅值（ G G G） ：综合 G x G_x Gx 和 G y G_y Gy 的结果，反映灰度变化的强度，有两种计算方式：
- 精确计算（欧几里得距离）： G = G x 2 + G y 2 G=\sqrt{G_x^2+G_y^2} G=Gx2+Gy2
  优点：精度高；缺点：涉及开方运算，计算量大。
- 近似计算（绝对值和）： G = ∣ G x ∣ + ∣ G y ∣ G=|G_x|+|G_y| G=∣Gx∣+∣Gy∣
  优点：计算速度快，避免浮点运算；缺点：精度略低。
  在OpenCV中，默认采用近似计算，平衡精度与效率。
梯度方向（ θ \theta θ） ：通过反正切函数计算，公式为：
θ = arctan ⁡ ( G y G x ) \theta=\arctan\left(\frac{G_y}{G_x}\right) θ=arctan(GxGy)

计算结果的范围是 [ − 9 0 ∘ , 9 0 ∘ ] [-90^\circ,90^\circ] [−90∘,90∘]，需映射到 [ 0 ∘ , 18 0 ∘ ] [0^\circ,180^\circ] [0∘,180∘]（边缘方向具有对称性， 0 ∘ 0^\circ 0∘ 与 18 0 ∘ 180^\circ 180∘ 方向一致）。

2.4 边缘方向分类

为后续非极大值抑制步骤做准备，需将梯度方向归为4个主要方向（与图像像素排列对齐），具体分类规则如下：

梯度方向范围	归类方向	对应边缘类型
− 22. 5 ∘ ∼ 22. 5 ∘ -22.5^\circ\sim22.5^\circ −22.5∘∼22.5∘ 或 157. 5 ∘ ∼ 18 0 ∘ 157.5^\circ\sim180^\circ 157.5∘∼180∘	0 ∘ 0^\circ 0∘	水平边缘（梯度垂直于边缘）
22. 5 ∘ ∼ 67. 5 ∘ 22.5^\circ\sim67.5^\circ 22.5∘∼67.5∘ 或 − 157. 5 ∘ ∼ − 112. 5 ∘ -157.5^\circ\sim-112.5^\circ −157.5∘∼−112.5∘	4 5 ∘ 45^\circ 45∘	4 5 ∘ 45^\circ 45∘ 边缘
67. 5 ∘ ∼ 112. 5 ∘ 67.5^\circ\sim112.5^\circ 67.5∘∼112.5∘ 或 − 112. 5 ∘ ∼ − 67. 5 ∘ -112.5^\circ\sim-67.5^\circ −112.5∘∼−67.5∘	9 0 ∘ 90^\circ 90∘	垂直边缘
112. 5 ∘ ∼ 157. 5 ∘ 112.5^\circ\sim157.5^\circ 112.5∘∼157.5∘ 或 − 67. 5 ∘ ∼ − 22. 5 ∘ -67.5^\circ\sim-22.5^\circ −67.5∘∼−22.5∘	13 5 ∘ 135^\circ 135∘	13 5 ∘ 135^\circ 135∘ 边缘

2.5 难点标注

梯度方向的近似误差：由于Sobel算子是离散核，计算出的梯度方向是近似值，尤其是在边缘灰度变化平缓的区域，可能导致方向归类错误，影响后续非极大值抑制效果。
零梯度处理：当 G x = 0 G_x=0 Gx=0 时， arctan ⁡ \arctan arctan 函数会出现无穷大，需特殊处理（直接将梯度方向设为 9 0 ∘ 90^\circ 90∘ 或 − 9 0 ∘ -90^\circ −90∘）。

3. 非极大值抑制

3.1 原理与目标

经过高斯滤波和梯度计算后，得到的边缘通常是"粗边缘"（多个相邻像素均被判定为边缘），不符合"一一对应"准则。非极大值抑制（Non-Maximum Suppression, NMS）的目标是：在梯度方向上，仅保留梯度幅值最大的像素，将其他像素抑制为0，从而将粗边缘细化为单像素宽度的细边缘。

3.2 实现步骤

确定邻域像素 ：根据当前像素 ( x , y ) (x,y) (x,y) 的梯度方向，确定其在梯度方向上的两个相邻像素（即沿边缘垂直方向的前后像素）：
- 若梯度方向为 0 ∘ 0^\circ 0∘（水平边缘）：邻域像素为 ( x − 1 , y ) (x-1,y) (x−1,y) 和 ( x + 1 , y ) (x+1,y) (x+1,y)（左右方向）；
- 若梯度方向为 4 5 ∘ 45^\circ 45∘：邻域像素为 ( x − 1 , y + 1 ) (x-1,y+1) (x−1,y+1) 和 ( x + 1 , y − 1 ) (x+1,y-1) (x+1,y−1)（左上-右下方向）；
- 若梯度方向为 9 0 ∘ 90^\circ 90∘（垂直边缘）：邻域像素为 ( x , y − 1 ) (x,y-1) (x,y−1) 和 ( x , y + 1 ) (x,y+1) (x,y+1)（上下方向）；
- 若梯度方向为 13 5 ∘ 135^\circ 135∘：邻域像素为 ( x − 1 , y − 1 ) (x-1,y-1) (x−1,y−1) 和 ( x + 1 , y + 1 ) (x+1,y+1) (x+1,y+1)（右上-左下方向）。
比较梯度幅值 ：将当前像素的梯度幅值 G ( x , y ) G(x,y) G(x,y) 与两个邻域像素的梯度幅值比较：
- 若 G ( x , y ) G(x,y) G(x,y) 是三者中的最大值：保留该像素，灰度值不变；
- 否则：将该像素抑制为0（非边缘）。

3.3 插值处理

上述步骤仅适用于梯度方向为 0 ∘ 0^\circ 0∘、 4 5 ∘ 45^\circ 45∘、 9 0 ∘ 90^\circ 90∘、 13 5 ∘ 135^\circ 135∘ 的情况，但实际计算出的梯度方向可能是任意角度（如 1 5 ∘ 15^\circ 15∘、 3 0 ∘ 30^\circ 30∘ 等）。此时，邻域像素并非整数坐标，需通过单线性插值计算非整数坐标处的梯度幅值。

以梯度方向为 22. 5 ∘ ∼ 67. 5 ∘ 22.5^\circ\sim67.5^\circ 22.5∘∼67.5∘（非标准 4 5 ∘ 45^\circ 45∘）为例，假设当前像素为 C C C，梯度方向上的非整数坐标点为 d T m p 1 dTmp1 dTmp1 和 d T m p 2 dTmp2 dTmp2，周围整数坐标像素为 A 1 A1 A1、 A 2 A2 A2、 A 3 A3 A3、 A 4 A4 A4，插值计算步骤如下：

根据梯度方向与像素坐标的偏移量，计算 d T m p 1 dTmp1 dTmp1 到 A 1 A1 A1、 A 2 A2 A2 的距离权重；
通过加权平均计算 d T m p 1 dTmp1 dTmp1 的梯度幅值： d T m p 1 = w 1 × A 1 + ( 1 − w 1 ) × A 2 dTmp1 = w1 \times A1 + (1-w1) \times A2 dTmp1=w1×A1+(1−w1)×A2（ w 1 w1 w1 为权重）；
同理计算 d T m p 2 dTmp2 dTmp2 的梯度幅值： d T m p 2 = w 2 × A 3 + ( 1 − w 2 ) × A 4 dTmp2 = w2 \times A3 + (1-w2) \times A4 dTmp2=w2×A3+(1−w2)×A4；
将 C C C 的梯度幅值与 d T m p 1 dTmp1 dTmp1、 d T m p 2 dTmp2 dTmp2 比较，保留最大值。

3.4 难点标注

插值精度与计算量的平衡：插值越复杂（如双线性插值），精度越高，但计算量越大；单线性插值是工程上的折中选择，需理解其误差来源。
边缘断裂风险：若梯度方向归类错误，会导致邻域像素选择错误，进而抑制真实边缘像素，造成边缘断裂。

4. 双阈值筛选

4.1 原理与必要性

非极大值抑制后，图像中仍存在由噪声残留导致的"假边缘"（非真实边缘的像素）。双阈值筛选通过设定两个阈值（高阈值 T h i g h T_{high} Thigh 和低阈值 T l o w T_{low} Tlow），对边缘像素进行分类筛选，区分"确定边缘""候选边缘"和"非边缘"。

4.2 阈值设定原则

经验比例： T h i g h : T l o w = 2 : 1 ∼ 3 : 1 T_{high}:T_{low}=2:1\sim3:1 Thigh:Tlow=2:1∼3:1（如 T h i g h = 70 T_{high}=70 Thigh=70， T l o w = 30 T_{low}=30 Tlow=30）；
影响：
- 阈值过高：会遗漏弱边缘（如模糊物体的边缘），导致边缘不完整；
- 阈值过低：会保留大量假边缘，影响后续处理。

4.3 筛选规则

强边缘（确定边缘）：若像素梯度幅值 G > T h i g h G>T_{high} G>Thigh，则该像素是边缘，直接保留；
非边缘：若像素梯度幅值 G < T l o w G<T_{low} G<Tlow，则该像素不是边缘，直接抑制为0；
弱边缘（候选边缘）：若 T l o w ≤ G ≤ T h i g h T_{low}\leq G\leq T_{high} Tlow≤G≤Thigh，则需进一步判断------若该像素与强边缘直接连通（邻域内有强边缘像素），则判定为边缘；否则，抑制为0。

4.4 滞后边界跟踪

弱边缘的判断需通过"滞后边界跟踪"实现：

遍历图像中所有强边缘像素，标记为"边缘"；
以强边缘像素为起点，遍历其8邻域内的弱边缘像素，将这些弱边缘像素标记为"边缘"；
重复步骤2，直到所有与强边缘连通的弱边缘都被标记；
未被标记的弱边缘像素（孤立弱边缘）抑制为0。

4.5 难点标注

阈值选择无通用标准：需根据图像的灰度分布、噪声强度调整，例如：
- 高对比度图像：可适当提高阈值，减少假边缘；
- 低对比度图像：需降低阈值，避免遗漏弱边缘；
连通性判断：8邻域连通（比4邻域连通）能保留更多连续边缘，但可能将相邻的假边缘误判为连通，需权衡。

5. 边缘输出

经过上述4个步骤后，最终得到的是二值图像------边缘像素灰度值为255（白色），非边缘像素灰度值为0（黑色），完成边缘检测的全部过程。

四、 Sobel算子

在Canny算法的梯度计算步骤中，Sobel算子是核心工具，其性能直接影响梯度计算的精度与抗噪声能力，需深入理解其特性与应用。

1. Sobel算子的定义与优势

Sobel算子是由Irwin Sobel于1968年在博士生课题讨论会上提出的离散微分算子，1973年通过专著脚注公开。其核心优势在于：

结合高斯平滑与微分：先通过加权平均实现平滑（抗噪声），再通过差分实现微分（捕捉梯度），兼顾去噪与边缘检测；
权重化设计：相邻像素对当前像素的影响随距离增大而减小（如水平Sobel核中，中间行的权重为-2、0、2，比上下行的-1、0、1更大），符合人眼对近邻像素更敏感的视觉特性；
计算效率高：采用3×3核，可通过快速卷积实现，适合实时处理。

2. Sobel算子的扩展

当使用3×3核计算梯度时，Sobel算子的方向精度有限。OpenCV提供了Scharr算子（aperture_size=-1时调用），是对3×3 Sobel算子的优化，其核权重更精确，方向检测误差更小，且计算速度与Sobel算子相同。

Scharr算子的核形式如下：

水平方向： [ − 3 0 3 − 10 0 10 − 3 0 3 ] \left[\begin{array}{ccc}-3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3\end{array}\right] −3−10−30003103
垂直方向： [ − 3 − 10 − 3 0 0 0 3 10 3 ] \left[\begin{array}{ccc}-3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3\end{array}\right] −303−10010−303

在需要高精度梯度方向的场景（如医学影像、工业质检），建议优先使用Scharr算子替代3×3 Sobel算子。

3. Sobel算子的局限性

无灰度自适应：未考虑图像灰度分布的差异，对灰度渐变的边缘检测效果较好，但对灰度突变的边缘（如黑白交界）可能出现过检测；
边缘定位精度有限：由于是离散核，梯度方向是近似值，可能导致边缘定位偏差，需结合非极大值抑制中的插值处理改善；
对噪声仍敏感：虽结合了高斯平滑，但对强噪声（如椒盐噪声）的抑制效果有限，需在高斯滤波前增加中值滤波等预处理步骤。

五、算法参数选择与优化建议

Canny算法的性能高度依赖参数设置，合理的参数能显著提升边缘检测效果，以下是关键参数的选择原则与优化建议：

1. 高斯核参数（ σ \sigma σ 与核大小）

σ \sigma σ 选择 ：
- 噪声少的图像（如合成图像）： σ = 0.8 ∼ 1.2 \sigma=0.8\sim1.2 σ=0.8∼1.2，核大小3×3或5×5；
- 噪声多的图像（如实拍图像）： σ = 1.4 ∼ 2.0 \sigma=1.4\sim2.0 σ=1.4∼2.0，核大小5×5或7×7；
核大小选择 ：核大小通常为 σ \sigma σ 的3-5倍（确保高斯函数的主要能量集中在核内），例如 σ = 1.4 \sigma=1.4 σ=1.4 对应5×5核。

2. 双阈值（ T h i g h T_{high} Thigh 与 T l o w T_{low} Tlow）

经验法 ：先计算图像梯度幅值的直方图，选择直方图中"峰值后的第一个谷值"作为 T h i g h T_{high} Thigh，再按2:1~3:1比例确定 T l o w T_{low} Tlow；
自适应法：通过Otsu算法自动计算阈值（适用于灰度分布均匀的图像）；
手动调整：在工程应用中，可提供交互式界面，让用户根据实时预览结果调整阈值（如OpenCV的Canny函数演示工具）。

3. 边缘连通性判断

连通域选择：优先使用8邻域连通（比4邻域连通能保留更多连续边缘），但需注意：若图像中噪声较多，8邻域可能导致假边缘连通，此时可先进行形态学滤波（如膨胀、腐蚀）去除小噪声块。

4. 预处理与后处理优化

预处理 ：若图像噪声严重，可在高斯滤波前增加中值滤波 （抑制椒盐噪声效果好）或双边滤波（保留边缘的同时去噪）；
后处理 ：边缘检测后，可通过形态学膨胀 （连接断裂的细小边缘）或腐蚀（去除孤立的小边缘点）优化边缘形态。

六、代码示例

python 复制代码

#导入opencv库
import cv2

#1.读取图像
image_np = cv2.imread('./picture.png')

#2.灰度化图像
image_gray = cv2.cvtColor(image_np,cv2.COLOR_BGR2GRAY)


#3.高斯滤波
image_blur = cv2.GaussianBlur(image_np,(5,5),1.5)

#4.进行边缘检测
image_canny = cv2.Canny(image_blur,30,70)

#5.显示结果
cv2.imshow('image_np',image_np)
cv2.imshow('image_canny',image_canny)
cv2.waitKey(0)

输出结果为:

七、常见问题与解决方案

在实际应用Canny算法时，常遇到边缘断裂、假边缘过多、边缘定位偏差等问题，以下是针对性的解决方案：

常见问题	原因分析	解决方案
边缘断裂	1. 阈值过高，弱边缘被抑制；2. 梯度方向归类错误；3. 噪声导致梯度幅值波动	1. 降低 T l o w T_{low} Tlow，扩大弱边缘范围；2. 使用Scharr算子提高梯度方向精度；3. 增加预处理（如双边滤波）
假边缘过多	1. 阈值过低，噪声被误判为边缘；2. 高斯滤波不充分	1. 提高 T h i g h T_{high} Thigh，减少假边缘；2. 增大高斯核 σ \sigma σ 或核大小；3. 增加后处理（如面积滤波，去除小边缘块）
边缘定位偏差	1. Sobel算子精度有限；2. 插值处理误差	1. 使用Scharr算子替代Sobel算子；2. 采用双线性插值替代单线性插值；3. 对边缘进行亚像素级优化（如基于二阶导数过零点）
边缘过粗	非极大值抑制不彻底	1. 检查梯度方向归类是否正确；2. 确保插值处理正确实现；3. 增加形态学腐蚀步骤，细化边缘

八、算法应用场景与局限性

1. 典型应用场景

1.1 工业质检

应用：零件表面裂纹检测、尺寸测量（如机械零件的边缘定位）；
优势：Canny算法能精确检测细小边缘，且抗噪声能力强，适合工业环境中的复杂图像。

1.2 医学影像

应用：CT影像中的器官边缘分割、眼底图像中的血管边缘检测；
优势：能保留弱边缘（如早期肿瘤的模糊边缘），且边缘定位精度高，为医学诊断提供准确依据。

1.3 自动驾驶

应用：车道线检测、障碍物边缘识别；
优势：实时性好（算法步骤简单，可硬件加速），且能处理不同光照条件下的图像（通过自适应阈值调整）。

1.4 图像配准

应用：遥感图像配准、全景图像拼接；
优势：边缘是图像的关键特征，Canny检测的边缘可作为配准的特征点，提高配准精度（如摘要5中提到的日冕图像配准，虽传统Canny效果有限，但改进版Canny仍有应用价值）。

2. 局限性

对纹理丰富的图像效果差：如草地、织物图像，纹理的灰度变化会被误判为边缘，导致边缘杂乱；
对光照变化敏感：同一物体在不同光照下的灰度分布不同，可能导致边缘检测结果不一致（需进行光照归一化预处理）；
无法处理彩色图像直接检测：Canny算法仅适用于灰度图像，若处理彩色图像，需先将其转换为灰度图像（如通过RGB转YUV，取Y通道作为灰度值），或对每个颜色通道分别检测后融合结果。

九、总结与展望

Canny边缘检测算法凭借其"最优边缘检测"的理论基础、清晰的步骤设计和优异的实践性能，成为计算机视觉领域的经典算法。其核心价值在于：通过高斯滤波、梯度计算、非极大值抑制、双阈值筛选的有机结合，在去噪与边缘保留之间取得了平衡，为后续高级视觉任务提供了高质量的边缘特征。

Canny算法的发展方向主要包括：

自适应参数优化：结合深度学习（如卷积神经网络），自动学习不同场景下的高斯核参数、双阈值等，减少人工干预；
多尺度边缘检测 ：通过多尺度高斯核（不同 σ \sigma σ）检测不同大小的边缘，再融合多尺度结果，提高边缘的完整性；
彩色图像直接检测：设计适用于彩色图像的Canny变体，利用颜色通道间的相关性，提升边缘检测的准确性；
实时硬件加速：针对嵌入式设备（如自动驾驶中的车载芯片），通过FPGA、GPU加速Canny算法的卷积、插值等计算密集型步骤，满足实时性要求。