算法练习：差分

差分用于快速解决"将某一个区间所有元素统一加上一个数"的操作

差分模板

差分数组定义：f[i] = a[i] - a[i-1];

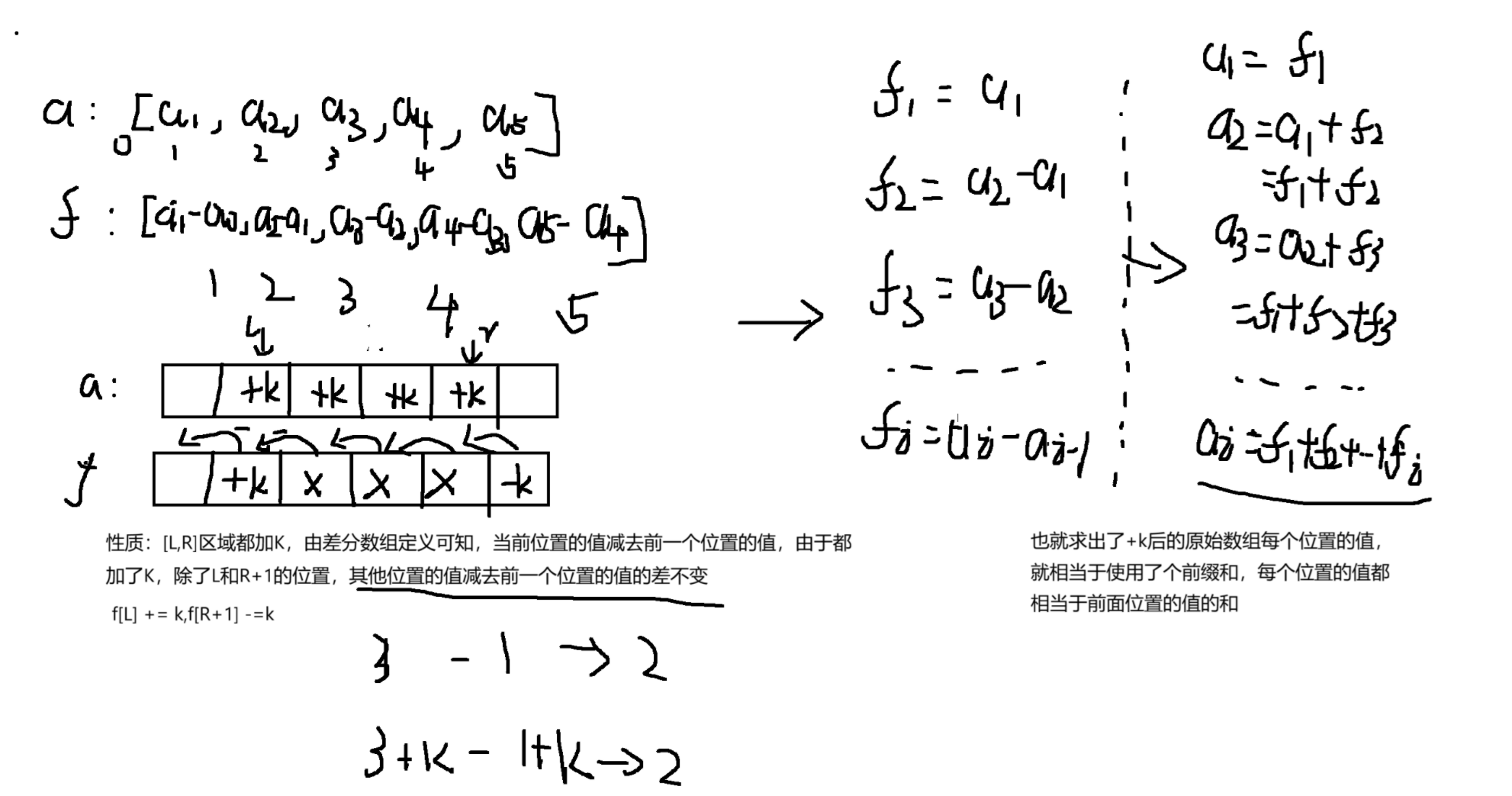
核心算法：

• 利用定义或性质初始化差分数组

//按定义初始化差分数组
    for(int i = 1; i <= n; i++)
    {
        cin>>a[i];
        f[i] = a[i] - a[i-1];
    }
    

//利用差分数组的性质
    for(int i = 1; i <= n; i++)
    {
        LL x;
        cin>>x;
        f[i] += x;
        f[i+1] -= x;
    }

• 根据性质，对差分数组进行m次操作

while(m--)
{
    int l,r,k;
    cin>>l>>r>>k;
    f[l] += k;
    f[r+1] -= k;
}

• 还原被操作后的原始数组

    for(int i = 1; i <= n; i++)
    {
        a[i] = a[i-1] + f[i] ;
        cout<<a[i]<<" ";
    }

 		for(int i = 1; i <= n; i++)
    {
        f[i] = f[i-1] + f[i];
        cout<<f[i]<<" ";
    }

注意：

差分数组使用的时候，所有的操作必须全部进行完毕之后，才能还原出操作之后的数组

如果要边操作边还原的话，差分数组就没用了，就可能要用到我们后面将要学的线段树之类的算法来解决

---

海底高铁

1. 题目背景与分析

题目大意 ：

你需要按顺序访问一系列城市（ P 1 , P 2 , ... , P m P_1, P_2, \dots, P_m P1,P2,...,Pm）。相邻两个城市 i i i 和 i + 1 i+1 i+1 之间有一段铁路。对于每一段铁路，你有两种付费方式：

1. 直接买票 ：单价为 a a a。
2. 办卡买票 ：先付办卡费 c c c，之后每次通过单价降为 b b b（通常 b < a b < a b<a）。

目标是求出按顺序走完所有旅程的最小总花费。

核心难点 ：

如果模拟每一次移动（例如从城市 1 走到城市 100），并对沿途每一段铁路的计数器加 1，时间复杂度会非常高，最坏情况下是 O ( N × M ) O(N \times M) O(N×M)，这会导致超时。

解决方案 ：

使用差分数组 将区间的修改操作（一段路经过次数 +1）的时间复杂度从 O ( N ) O(N) O(N) 降低到 O ( 1 ) O(1) O(1)。

---

2. 核心算法逻辑

• 统计每段铁路的经过次数

  我们用 f [ i ] f[i] f[i] 表示城市 i i i 到城市 i + 1 i+1 i+1 这段铁路被经过的次数。

  当我们从城市 x x x 移动到城市 y y y 时（假设 x < y x < y x<y），不仅是经过 x x x 和 y y y，而是经过区间 [ x , y ) [x, y) [x,y) 内的所有铁路段，即段 x , x + 1 , ... , y − 1 x, x+1, \dots, y-1 x,x+1,...,y−1 的经过次数都要 + 1 +1 +1。

利用差分数组的思想：

• 若 x < y x < y x<y：f[x]++, f[y]--
• 若 x > y x > y x>y：f[y]++, f[x]-- （相当于区间 [ y , x ) [y, x) [y,x) 加 1）

注意 ：这里之所以右端点减 1（即在 y y y 而不是 y + 1 y+1 y+1 处减），是因为 f [ i ] f[i] f[i] 代表的是 i → i + 1 i \to i+1 i→i+1 这段路。从 x x x 走到 y y y，最后一段路是 y − 1 → y y-1 \to y y−1→y，并不包含 y → y + 1 y \to y+1 y→y+1。

• 还原真实次数（前缀和）

  输入处理完所有旅程后，当前的 f f f 数组只是差分值。我们需要对其求前缀和，才能得到每段路实际被经过的总次数。
  f [ i ] = f [ i ] + f [ i − 1 ] f[i] = f[i] + f[i-1] f[i]=f[i]+f[i−1]

• 贪心计算最小花费

  对于每一段铁路 i i i：

  • 方案 A （不办卡）：花费 = 经过次数 × a \times a ×a
  • 方案 B （办卡）：花费 = 经过次数 × b + c \times b + c ×b+c

对于每一段路，我们取 min(方案A, 方案B) 加入总花费即可。

---

代码详解

#include <iostream>
using namespace std;

typedef long long LL; // 结果可能很大，必须使用 long long
const int N = 1e5+10; // 根据题目数据范围设定，通常是 10^5

int n, m;
LL f[N]; // 差分数组，计算后变为计数数组

int main()
{
    cin >> n >> m; // n: 城市数量, m: 计划访问的城市序列长度
    int x;
    cin >> x; // 读取起点的城市编号

    // [L, R-1] 区间更新逻辑
    for(int i = 2; i <= m; i++)
    {
        int y;
        cin >> y; // 读取下一个目的地
        if(x > y)
        {
            // 从 x 走到 y (向左走)，覆盖区间 [y, x-1]
            // 差分操作：左端点+1，右端点+1的位置-1
            f[y]++;
            f[x]--;
        }
        else
        {
            // 从 x 走到 y (向右走)，覆盖区间 [x, y-1]
            f[x]++;
            f[y]--;
        }
        x = y; // 更新当前位置为起点，准备下一段旅程
    }

    // 核心步骤：前缀和还原
    // 此时 f[i] 存储的是城市 i 到 i+1 这段路经过的总次数
    for(int i = 1; i <= n; i++)
    {
        f[i] = f[i-1] + f[i];
    }

    LL ret = 0; // 总费用
    // 遍历每一段铁路（共有 n-1 段，对应下标 1 到 n-1）
    for(int i = 1; i < n; i++)
    {
        LL a, b, c;
        cin >> a >> b >> c; // a:原价, b:折后价, c:办卡费
        
        // 贪心策略：比较"直接买票总价"与"办卡+折后买票总价"
        // 注意：f[i] 是第 i 段路的经过次数
        ret += min(a * f[i], c + b * f[i]);
    }
    cout << ret;
}

---

复杂度分析

• 时间复杂度 ： O ( N + M ) O(N + M) O(N+M)
  • 处理 M M M 个行程点的差分更新是 O ( M ) O(M) O(M)。
  • 求前缀和还原数组是 O ( N ) O(N) O(N)。
  • 最后计算总费用遍历边是 O ( N ) O(N) O(N)。
  • 因为 N , M ≤ 1 0 5 N, M \le 10^5 N,M≤105，程序运行非常快，完全能满足 1秒 的时限。
• 空间复杂度 ： O ( N ) O(N) O(N)
  • 只需要一个数组 f 来存储差分和计数信息。

易错点总结

1. 数据类型 ：总费用 ret 可能会超过 int 的范围（最大约为 1 0 5 × 1 0 5 × cost 10^5 \times 10^5 \times \text{cost} 105×105×cost），所以必须使用 long long。
2. 差分边界 ：
   • 铁路是连接 i i i 和 i + 1 i+1 i+1 的。
   • 如果是从 1 1 1 走到 4 4 4，经过的铁路是 1 − 2 , 2 − 3 , 3 − 4 1-2, 2-3, 3-4 1−2,2−3,3−4。对应数组下标 1 , 2 , 3 1, 2, 3 1,2,3。
   • 差分操作应该是 f[1]++, f[4]--。很多初学者会误写成 f[4]++ 或者 f[5]--。
3. 循环范围 ：计算费用时，循环是 1 到 n-1，因为 n n n 个城市之间只有 n − 1 n-1 n−1 段铁路。

---

二维差分主要用于解决在二维矩阵中对某个子矩阵（矩形区域）进行频繁的加减操作的问题。

---

二维差分模版

1.核心思想

暴力法的局限 ：

如果用双重循环直接修改矩阵，单次操作的时间复杂度是 O ( N × M ) O(N \times M) O(N×M)。如果有 q q q 次操作，总复杂度为 O ( q ⋅ N M ) O(q \cdot NM) O(q⋅NM)，这在数据量稍大时会立刻超时。

二维差分优化 ：

利用二维差分数组，我们可以将对"一个区域"的修改，转化为对"四个点"的修改。
时间复杂度：

• 修改操作 ： O ( 1 ) O(1) O(1)
• 最终还原 ： O ( N × M ) O(N \times M) O(N×M)
• 总复杂度 ： O ( N × M + q ) O(N \times M + q) O(N×M+q)

---

2. 核心逻辑详解

A. 差分矩阵的定义

设原矩阵为 A A A，差分矩阵为 F F F。

它们的关系是： A [ i ] [ j ] A[i][j] A[i][j] 等于 F F F 矩阵中 ( i , j ) (i, j) (i,j) 左上角所有元素的和（即 F F F 的二维前缀和）。

B. 修改操作（Insert 函数）

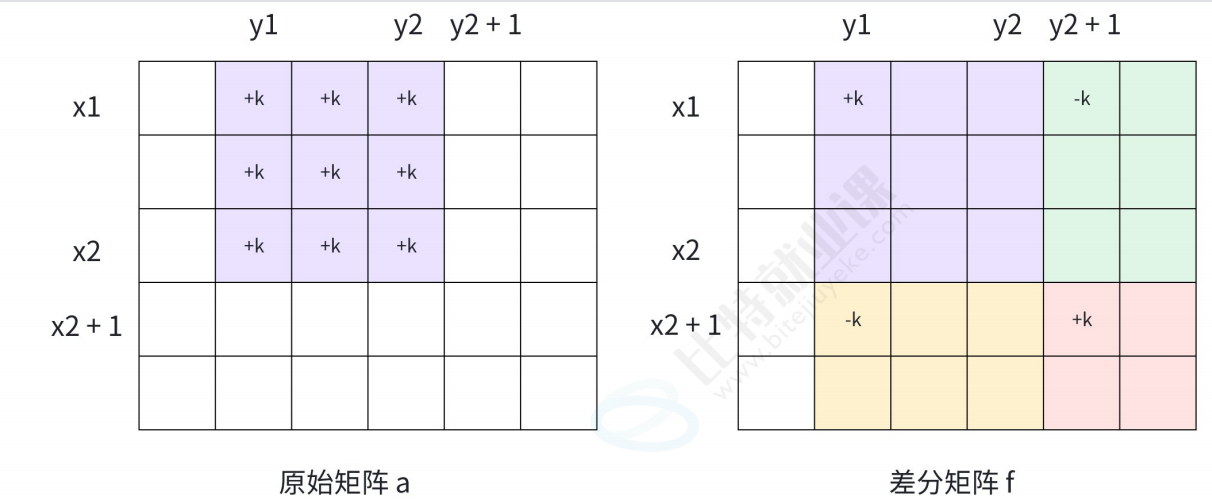
要在原矩阵 A A A 的子矩形 ( x 1 , y 1 ) ∼ ( x 2 , y 2 ) (x_1, y_1) \sim (x_2, y_2) (x1,y1)∼(x2,y2) 上加上 k k k，等价于在差分矩阵 F F F 上修改 4 个点：

void insert(int x1, int y1, int x2, int y2, int k)
{
    f[x1][y1] += k;        // 1. 作用于整个右下角
    f[x1][y2+1] -= k;      // 2. 剔除右侧多余部分
    f[x2+1][y1] -= k;      // 3. 剔除下方多余部分
    f[x2+1][y2+1] += k;    // 4. 补回因重复剔除而缺失的右下角重叠部分
}

原理图解：

1. f[x1][y1] += k：从 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 开始，其右下方的所有点在求前缀和时都会加上 k k k。
2. f[x1][y2+1] -= k：为了限制修改范围不超过右边界 y 2 y_2 y2，我们需要在 y 2 + 1 y_2+1 y2+1 处减去 k k k，抵消掉上面的增加。
3. f[x2+1][y1] -= k：同理，为了限制不超过下边界 x 2 x_2 x2，在 x 2 + 1 x_2+1 x2+1 处减去 k k k。
4. f[x2+1][y2+1] += k：由于步骤 2 和 3 对右下角的重叠区域 ( x 2 + 1 , y 2 + 1 ) (x_2+1, y_2+1) (x2+1,y2+1) 各减了一次（共减了 2 k 2k 2k），而步骤 1 加了 1 k 1k 1k，导致这里实际上减了 k k k。为了保持该区域不变（因为它是操作区域的外部），我们需要再加回 k k k（容斥原理）。
   

C. 初始化的技巧

// 读入初始矩阵时
cin >> x;
insert(i, j, i, j, x);

解释 ：

通常我们需要根据公式 F [ i ] [ j ] = A [ i ] [ j ] − A [ i − 1 ] [ j ] − A [ i ] [ j − 1 ] + A [ i − 1 ] [ j − 1 ] F[i][j] = A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1] F[i][j]=A[i][j]−A[i−1][j]−A[i][j−1]+A[i−1][j−1] 来构造初始的差分矩阵。

但这里我们可以换个思路：把初始矩阵看作是一个全 0 矩阵 ，然后在位置 ( i , j ) (i, j) (i,j) 到 ( i , j ) (i, j) (i,j) 这个 1 × 1 1 \times 1 1×1 的矩形范围内插入了数值 x x x。

这样复用 insert 函数，代码更加简洁统一。

D. 还原矩阵（二维前缀和）

操作全部完成后，我们需要对差分矩阵求二维前缀和 来得到最终结果：
F [ i ] [ j ] = F [ i − 1 ] [ j ] + F [ i ] [ j − 1 ] − F [ i − 1 ] [ j − 1 ] + 当前差分值 F[i][j] = F[i-1][j] + F[i][j-1] - F[i-1][j-1] + \text{当前差分值} F[i][j]=F[i−1][j]+F[i][j−1]−F[i−1][j−1]+当前差分值

代码对应：

f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + f[i][j];

---

代码详解：

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, m, q;
LL f[N][N]; // 差分矩阵

void insert(int x1,int y1,int x2,int y2,int k)
{
    f[x1][y1] += k;
    f[x1][y2+1] -= k;
    f[x2+1][y1] -= k;
    f[x2+1][y2+1] += k;
}

int main()
{
    cin>>n>>m>>q;
    for(int i = 1; i <= n; i++)
    {
        for(int j =1; j <= m; j++)
        {
            LL x;
            cin>>x;
            insert(i,j,i,j,x);
        }
        
    }
    
    while(q--)
    {
        int x1,y1,x2,y2,k;
        cin>>x1>>y1>>x2>>y2>>k;
        insert(x1,y1,x2,y2,k);
    }
    
    for(int i =1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + f[i][j];
            cout<<f[i][j]<<" ";
        }
        cout<<endl;
    }
    
    
    return 0;
}

---

地毯

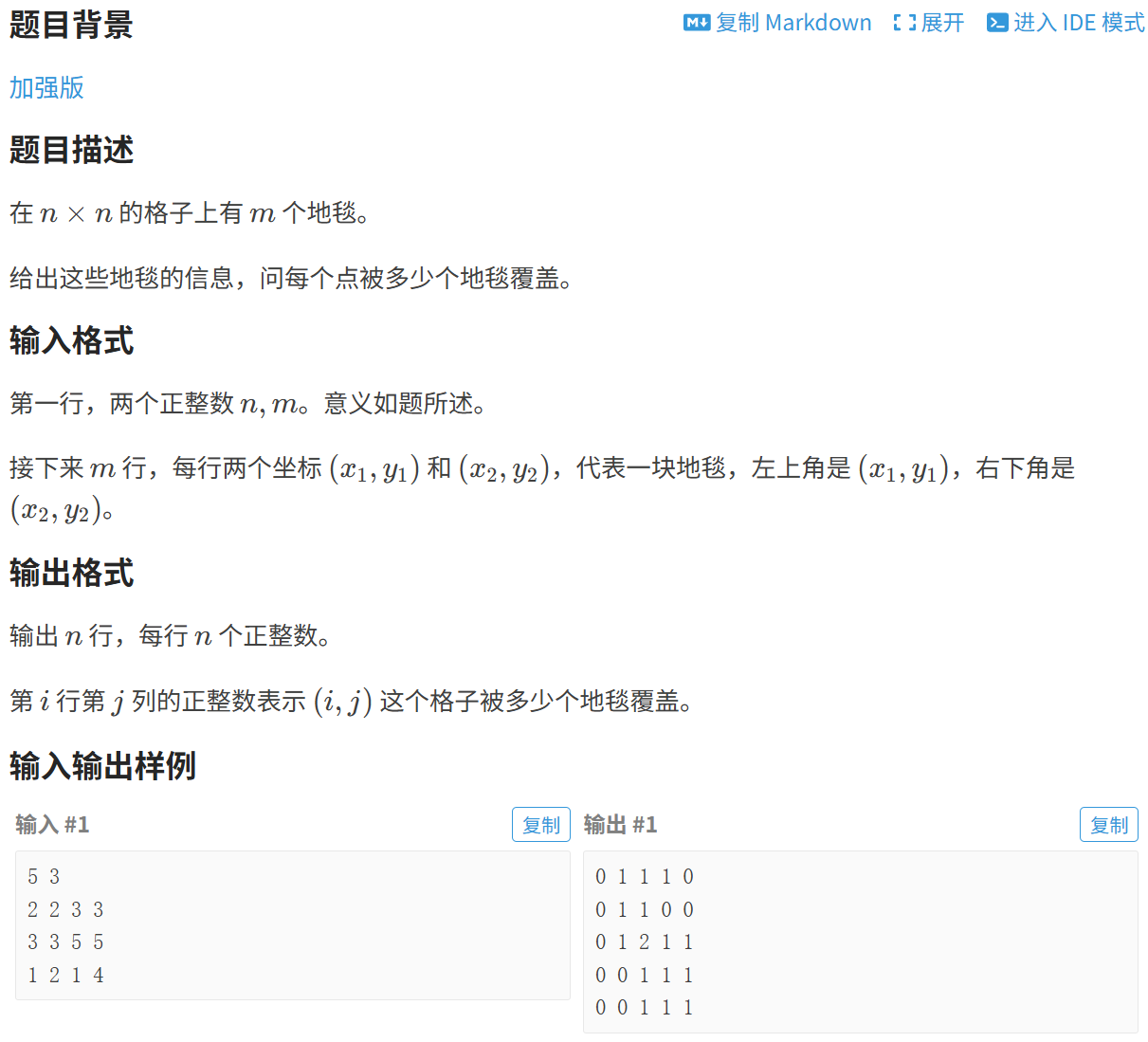
核心思想：

对二维差分模板的直接使用，在此不再过多赘述

---

代码详解：

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, m, q;
LL f[N][N]; // 差分矩阵

void insert(int x1,int y1,int x2,int y2,int k)
{
    f[x1][y1] += k;
    f[x1][y2+1] -= k;
    f[x2+1][y1] -= k;
    f[x2+1][y2+1] += k;
}

int main()
{
    cin>>n>>m;
    while(m--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        insert(x1,y1,x2,y2,1);
    }

    for(int i =1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + f[i][j];
            cout<<f[i][j]<<" ";
        }
        cout<<endl;
    }
}

---