这是一篇基于我们之前的对话内容整合而成的深度技术文章。文章从你提供的关于"显存与带宽限制"的精辟论述出发,深入剖析了 Llama-3-70B 的实际数据,对比了 MHA 与 GQA 的巨大差异,并探讨了 LLM 推理系统的核心瓶颈。
破解 LLM 推理的"显存墙"与"通信墙":从显存分布到部署原则
引言:推理系统的双重束缚
众所周知,一般情况下 LLM 的推理都是在 GPU 上进行。单张 GPU 的显存是有限的,这构成了大模型落地的第一道物理屏障。显存的占用主要分为两大部分:
- 静态显存(Static Memory) :用于存放模型的参数(Weights)和前向计算的临时激活值(Activations)。这部分依赖于模型的体量,一旦选定模型(如 70B 或 405B),它几乎就是一个固定的常数,是我们进入游戏的"门票"。
- 动态显存(Dynamic Memory) :主要用于存放 KV Cache。这部分不仅依赖于模型的体量,更强依赖于模型的输入长度(Context Length)和并发量(Batch Size)。在推理过程中,它是动态线性增长的。当 Context 长度足够长时,它的大小就会反客为主,占据主导地位,甚至轻松超出一张卡、一台机(8张卡)的总显存量。
在 GPU 上部署模型有一个黄金原则:能一张卡部署的,就不要跨多张卡;能一台机部署的,就不要跨多台机。
这是因为数据传输遵循严格的物理层级: "卡内通信带宽(SRAM ↔ HBM) > 卡间通信带宽(NVLink) > 机间通信带宽(Infiniband/Ethernet)" 。由于"木桶效应",模型部署时跨越的物理设备越多,受低速通信带宽的"拖累"就越大。事实上,即便是目前最顶级的 H100,其卡内显存带宽(HBM3)虽然达到了 3TB/s,但对于 Short Context 推理(Memory Bound 场景)来说,这个速度依然是瓶颈,更不用说速度下降数个数量级的卡间和机间通信了。
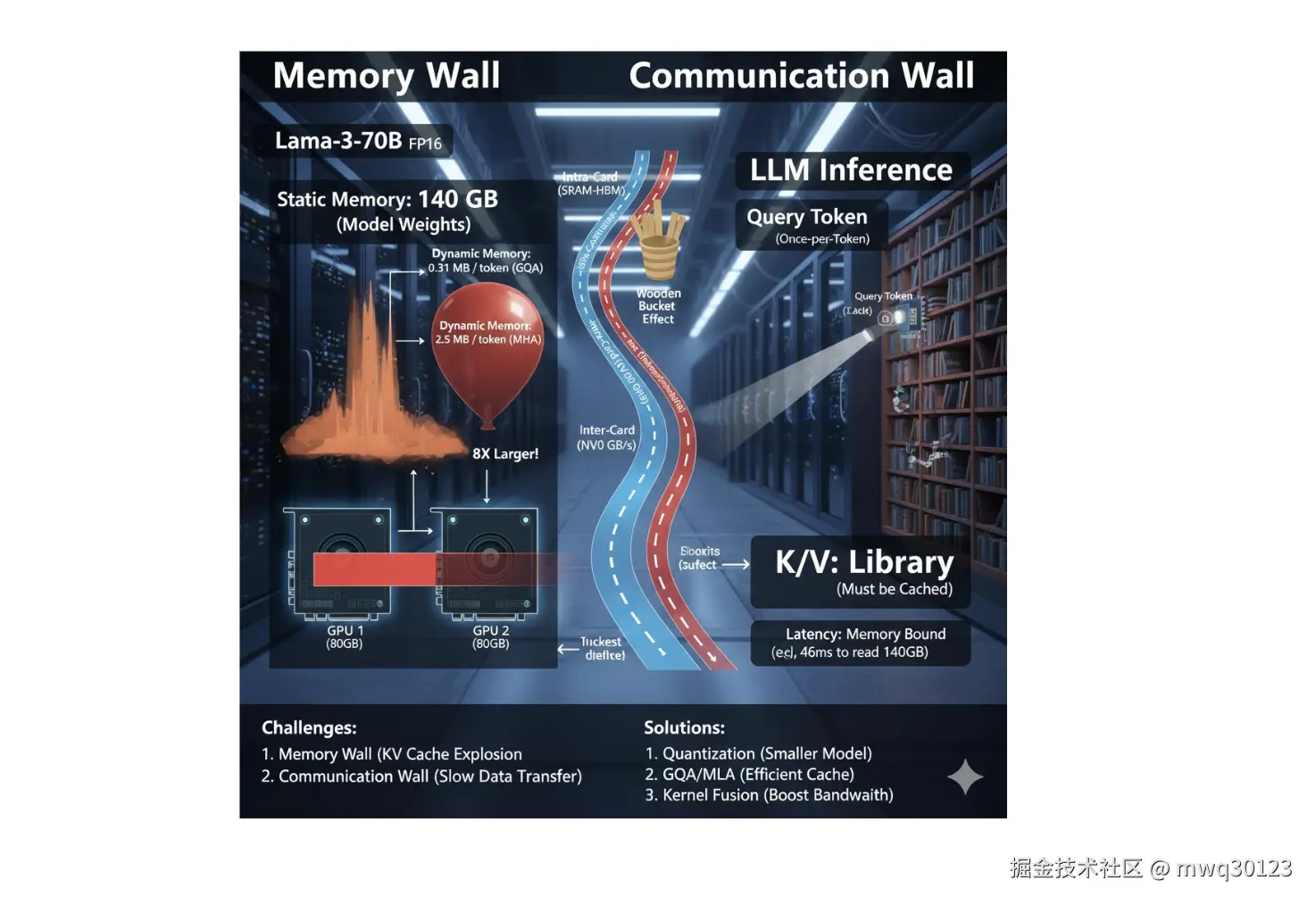
一、 显存账本:Llama-3-70B 的真实开销
为了具象化理解上述原则,我们以 Llama-3-70B 模型在 FP16 精度下的部署为例,算一笔显存的账。
1. 静态显存:昂贵的入场券
Llama-3-70B 拥有 700 亿参数。在 FP16 精度下,每个参数占用 2 Bytes。
<math xmlns="http://www.w3.org/1998/Math/MathML"> Static Usage ≈ 70 × 1 0 9 × 2 Bytes ≈ 140 GB \text{Static Usage} \approx 70 \times 10^9 \times 2 \text{ Bytes} \approx \mathbf{140 \text{ GB}} </math>Static Usage≈70×109×2 Bytes≈140 GB
这意味着,仅仅是为了加载模型,你就至少需要 2张 80GB 的 A100/H100。如果只有一张卡,连模型都无法启动。这 140GB 是雷打不动的"固定成本"。
2. 动态显存:被忽视的隐形杀手
动态显存的核心是 KV Cache。它存储了所有历史 Token 的键(Key)和值(Value),以避免重复计算。Llama-3-70B 采用了 GQA(分组查询注意力) 技术,将 KV Heads 的数量压缩到了 8 个。
在此架构下,每生成或处理 1 个 Token,其 KV Cache 的显存占用约为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Mem token ≈ 0.31 MB \text{Mem}_{\text{token}} \approx \mathbf{0.31 \text{ MB}} </math>Memtoken≈0.31 MB
文章底部有计算过程
看似很小?让我们看看在不同场景下的总账:
-
场景 A(长文档分析) :Batch Size=1,Context=32k。
- KV Cache <math xmlns="http://www.w3.org/1998/Math/MathML"> ≈ 10 GB \approx 10 \text{ GB} </math>≈10 GB。此时 2张卡(共160GB,剩20GB可用)还能勉强应付。
-
场景 B(高并发服务) :Batch Size=64,Context=2k。
- KV Cache <math xmlns="http://www.w3.org/1998/Math/MathML"> ≈ 41 GB \approx 41 \text{ GB} </math>≈41 GB。
- 结果 :此时总显存需求达到 181GB,2张卡直接显存溢出(OOM) ,系统崩溃。
这验证了引言中的判断:在长文本或高并发场景下,动态显存会迅速吞噬剩余空间,迫使我们增加更多昂贵的 GPU。
二、 架构的演进:为何 MHA 正在被抛弃?
为了解决"动态显存爆炸"的问题,现代大模型(如 Llama 3, Mistral)纷纷抛弃了传统的 MHA(多头注意力) ,转而使用 GQA(分组查询注意力) 。
我们可以做一个反事实假设:如果 Llama-3-70B 坚持使用 MHA,会发生什么?
在 MHA 架构下,KV Heads 的数量必须与 Query Heads 一致(64个),这意味着 KV Cache 的大小将直接翻 8 倍。
| 指标 | Llama-3-70B (实际 GQA) | Llama-3-70B (假设 MHA) |
|---|---|---|
| 单 Token 显存占用 | 0.31 MB | 2.5 MB |
| 32k 长文 (BS=1) | 10 GB (轻松) | 80 GB (占满一张 H100) |
| 128k 超长文 (BS=1) | 40 GB (可接受) | 320 GB (灾难级) |
如果使用 MHA,仅为了处理一个 128k 的长文本请求,光是 KV Cache 就需要 4张 H100 ,加上权重则需要 6-8张 。这将导致推理成本高到无法商业化。因此,从 MHA 向 GQA/MLA 的演进,本质上是一场为了在有限显存内塞入更长 Context 的自救运动。
三、 带宽瓶颈:不仅仅是存不下
当我们被迫因为显存不足而增加 GPU 数量时(从单卡 -> 多卡 -> 多机),我们立刻撞上了第二道墙:通信带宽。
LLM 的推理过程(Decoding 阶段)是一个典型的 Memory Bound(内存受限) 任务。
- 计算核心(Tensor Core) 像是一个切菜极快的厨师(算力过剩)。
- 显存(HBM) 像是冰箱。
- 每生成一个 Token,厨师都需要把冰箱里重达 140GB 的食材(权重)全部搬运一遍,切一刀,然后放回去。
即便 H100 的 HBM3 带宽高达 3TB/s,搬运一次 140GB 数据也需要约 46ms 。这意味着,理论上限每秒只能生成约 20 个 Token。
而一旦我们将模型切分到多台机器(Model Parallelism):
- 计算不再是瓶颈,网络成了瓶颈。
- 设备间通信带宽从 3TB/s 骤降至 50-100GB/s(Infiniband)。
- 每一次矩阵乘法(Matrix Multiplication)都需要在机器间同步数据。
- 原本 46ms 的延迟可能会变成 500ms 甚至更高,导致用户体验产生极其明显的卡顿。
结语
理解了显存的静态与动态分布,以及通信带宽的层级差异,我们就能明白当前大模型推理优化的核心逻辑:
- 量化(Quantization) :通过 Int8/Int4 压缩静态权重,试图把 70B 模型塞进单卡或更少的卡中,避免跨设备通信。
- 架构改良(GQA/MLA) :通过减少 KV Cache 的体积,延缓动态显存的溢出,从而支持超长上下文(Long Context)。
- 算子融合(Kernel Fusion) :减少数据在 HBM 和 SRAM 之间的搬运次数,突破带宽瓶颈。
在显存墙与带宽墙被彻底打破之前, "能单卡不跨卡,能单机不跨机" 将始终是 LLM 部署的最高准则。
单个 Token 的 KV Cache 显存占用计算
以下是 Llama-3-70B 单个 Token 的 KV Cache 显存占用计算公式的详细推导过程。
1. 通用计算公式
任何 Transformer 类模型的 KV Cache(每个 Token)显存占用公式如下:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Mem token = 2 × n layers × n kv_heads × d head × P bytes \text{Mem}{\text{token}} = 2 \times n{\text{layers}} \times n_{\text{kv\heads}} \times d{\text{head}} \times P_{\text{bytes}} </math>Memtoken=2×nlayers×nkv_heads×dhead×Pbytes
参数含义拆解:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 2 </math>2 :代表 Key 和 Value 两个矩阵(Query 不需要缓存)。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> n layers n_{\text{layers}} </math>nlayers :模型的总层数(Layers)。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> n kv_heads n_{\text{kv\_heads}} </math>nkv_heads :用于存储 KV 的注意力头数量(GQA/MQA 架构下,这个数值小于 Query 头数)。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> d head d_{\text{head}} </math>dhead :单个注意力头的维度大小。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> P bytes P_{\text{bytes}} </math>Pbytes :数据精度占用的字节数(FP16/BF16 通常为 2 Bytes)。
2. Llama-3-70B 的具体参数代入
根据 Llama-3-70B 的架构配置:
-
精度 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> P bytes P_{\text{bytes}} </math>Pbytes) :通常推理使用 FP16,即 2 Bytes。
-
层数 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> n layers n_{\text{layers}} </math>nlayers) :80 层。
-
KV 头数 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> n kv_heads n_{\text{kv\_heads}} </math>nkv_heads) :
- Llama-3-70B 使用了 GQA (Grouped Query Attention) 。
- 虽然它的 Query Heads 是 64,但 KV Heads 被压缩到了 8。
-
单头维度 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> d head d_{\text{head}} </math>dhead) :
- 计算公式: <math xmlns="http://www.w3.org/1998/Math/MathML"> Hidden Size / Query Heads \text{Hidden Size} / \text{Query Heads} </math>Hidden Size/Query Heads
- <math xmlns="http://www.w3.org/1998/Math/MathML"> 8192 / 64 = 128 8192 / 64 = \mathbf{128} </math>8192/64=128。
3. 计算步骤
将上述数值代入公式:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Mem token = 2 × 80 × 8 × 128 × 2 (Bytes) = 160 × 8 × 256 = 1280 × 256 = 327 , 680 Bytes \begin{aligned} \text{Mem}_{\text{token}} &= 2 \times 80 \times 8 \times 128 \times 2 \text{ (Bytes)} \\ &= 160 \times 8 \times 256 \\ &= 1280 \times 256 \\ &= \mathbf{327,680 \text{ Bytes}} \end{aligned} </math>Memtoken=2×80×8×128×2 (Bytes)=160×8×256=1280×256=327,680 Bytes
4. 单位换算(Bytes <math xmlns="http://www.w3.org/1998/Math/MathML"> → \to </math>→ MB)
将字节转换为兆字节(MB):
<math xmlns="http://www.w3.org/1998/Math/MathML"> Mem token (MB) = 327 , 680 1024 × 1024 ≈ 0.3125 MB \text{Mem}_{\text{token (MB)}} = \frac{327,680}{1024 \times 1024} \approx \mathbf{0.3125 \text{ MB}} </math>Memtoken (MB)=1024×1024327,680≈0.3125 MB
这就是文中提到的 0.31 MB 的由来。
补充:如果是 MHA 会怎样?
如果取消 GQA,改回传统的 MHA,则 <math xmlns="http://www.w3.org/1998/Math/MathML"> n kv_heads n_{\text{kv\_heads}} </math>nkv_heads 会从 8 变成 64。
计算结果直接乘以 8:
<math xmlns="http://www.w3.org/1998/Math/MathML"> 0.3125 MB × 8 = 2.5 MB 0.3125 \text{ MB} \times 8 = \mathbf{2.5 \text{ MB}} </math>0.3125 MB×8=2.5 MB
这就是为什么 GQA 对于显存优化如此重要的数学证明。