斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记

- 前言
- [1. Motivation today](#1. Motivation today)
- [2. Scaling in practice](#2. Scaling in practice)
- [3. Maximum update parametrization -- in depth](#3. Maximum update parametrization – in depth)
- [4. CerebrasGPT](#4. CerebrasGPT)
- [5. MiniCPM](#5. MiniCPM)
- - [5.1 Techique 1: muP to stabilize scaling](#5.1 Techique 1: muP to stabilize scaling)
  - [5.2 Optimal batch size and LR](#5.2 Optimal batch size and LR)
  - [5.3 What remains -- model size vs data tradeoffs](#5.3 What remains – model size vs data tradeoffs)
  - [5.4 (partial) solution in miniCPM -- WSD learning rate](#5.4 (partial) solution in miniCPM – WSD learning rate)
  - [5.5 Side note -- other ways of estimating chinchilla curves](#5.5 Side note – other ways of estimating chinchilla curves)
  - [5.6 Chinchilla-type analysis](#5.6 Chinchilla-type analysis)
- [6. DeepSeek](#6. DeepSeek)
- [7. Recent scaling law recipes](#7. Recent scaling law recipes)
- - [7.1 LLaMA 3 (2024) Scaling laws](#7.1 LLaMA 3 (2024) Scaling laws)
  - [7.2 Hunyuan-1 (2024) large scaling laws](#7.2 Hunyuan-1 (2024) large scaling laws)
  - [7.3 MiniMax-01 (2025)](#7.3 MiniMax-01 (2025))
  - [7.4 Summary](#7.4 Summary)
- [8. Validating and understanding muP](#8. Validating and understanding muP)
- - [8.1 What is muP, anyway?](#8.1 What is muP, anyway?)
  - [8.2 Deriving muP (condition A1)](#8.2 Deriving muP (condition A1))
  - [8.3 Deriving muP (condition A2)](#8.3 Deriving muP (condition A2))
  - [8.4 muP mini recap..](#8.4 muP mini recap..)
  - [8.5 Implementation in Cerebras GPT](#8.5 Implementation in Cerebras GPT)
  - [8.6 Deeper dive into muP](#8.6 Deeper dive into muP)
  - [8.7 What is muP robust to?](#8.7 What is muP robust to?)
  - [8.8 Recap: scaling in the wild](#8.8 Recap: scaling in the wild)
- 结语
- 参考

前言

学习斯坦福的 CS336 课程，本篇文章记录课程第十一讲：推理，记录下个人学习笔记，仅供自己参考😄

website：https://stanford-cs336.github.io/spring2025

video：https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_

materials：https://github.com/stanford-cs336/spring2025-lectures

course material：https://stanford-cs336.github.io/spring2025-lectures/blob/lecture_11-Scaling_details.pdf

1. Motivation today

今天是缩放定律的第二讲，也是最后一讲，今天的课程将更侧重于案例研究和细节分析，我们将讲解两个独立的内容模块。第一部分内容，我们将详细分析几篇论文，这些研究在构建模型时都进行了严谨的缩放定律实验，我们将通过这些案例向大家展示现代语言模型开发者如何将缩放定律融合模型设计流程

上次和今天的课程核心在于探讨：扩展大模型的最佳实践是什么，我们的目标是构建具备优质超参数和合理架构选择的大语言模型，此前我们已经介绍过 Chinchilla 模型以及如何运用缩放定律验证这些设计要素，但大家理应对缩放定律保持合理的质疑态度，它本质上只是对数坐标下的曲线拟合，它真能像我们上次课说的那样可靠吗？

那么 Chinchilla 采用的缩放定律方法真的有效吗？如果仅拟合等计算量曲线，这真能反映最优的 token 取舍策略吗？这些方法真能用来确定最优学习率吗？我们是否应该选择特定的架构或参数化方法来实现更好的扩展性？这些问题大家都可以通过课后的实践作业逐步验证

2. Scaling in practice

我们上次课深入讨论的包含大量研究细节的最新论文，正是 DeepMind 的 Chinchilla 论文，此后，ChatGPT 横空出世，LLMs 研发的竞争格局就此彻底改变，自此，业界对训练数据、模型扩展等关键技术细节的公开讨论戛然而止，整个行业进入了高度保密的阶段，因此我们只能通过其他渠道来了解实际应用中的模型扩展方法

目前已有多个经过专业验证的大规模模型成功实现了扩展，在去年的课程中，我们重点讲解了 Cerebras-GPT、DeepSeek LLM 和 MiniCPM 三大模型，值得一提的是，去年我讲解这些中国模型时，还不得不专门解释选择它们的理由，但今年情况不同了，值得欣慰的是，现在提到 DeepSeek 时，大家已经自发表现出兴趣了，不再需要费力论证这些内容的价值

实际上，在缩放定律新发现和论文产出方面，这个领域反而显得异常冷清，我们将简要介绍去年未发布的 Llama 3 的部分研究成果、中国的混合专家模型 Hunyuan-large，其次是今年推出的 MiniMax 01---这个采用线性时间混合注意力机制的模型，专攻长上下文处理

虽然提到的这三者都进行了扩展性研究，但论研究深度与广度都远不及 DeepSeek 和 MiniCPM，这两个模型已然成为现代缩放定律研究的标杆

3. Maximum update parametrization -- in depth

首先需要深入探讨的是上次课提到的 μ P \mu P μP 参数化方法，简单回顾上节课内容： μ P \mu P μP 方法的核心在于，当我们扩大模型规模时，必须通过调整特定超参数

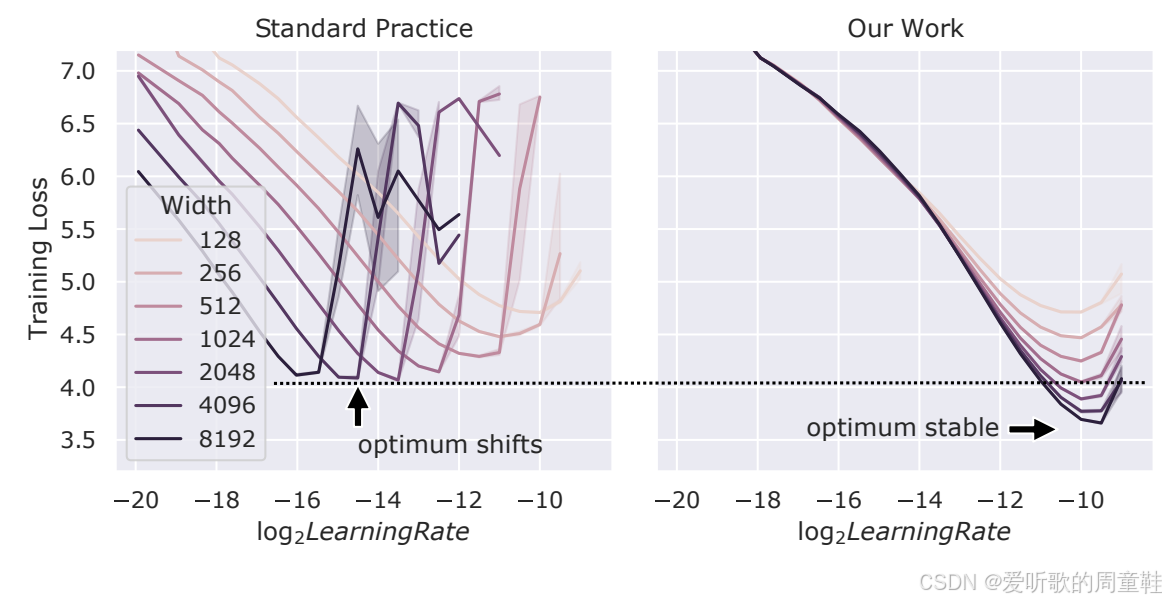
在左侧图可以看到，随着模型（本例中为 MLP 网络）宽度增加，最优学习率会逐渐下降，因此模型规模越大，所需学习率反而越小，这可能导致严重问题，因为在大规模训练时需要进行学习率调参，而这类超参数优化会带来极高的计算成本，这将成为重大瓶颈。反之，若能通过参数化方法使最优学习率在所有规模下保持恒定，那将实现重大突破，这也将极大简化参数搜索流程

我们希望所有超参数乃至整体架构选择都能在不同规模下保持稳定，这才是理想状态。最大更新参数化（ μ P \mu P μP）正是这一类极具突破性的解决方案，这种方法为我们提供了极具启发性的问题解决思路，接下来我们将具体阐述其中的数学原理细节，随后介绍第三方研究者对最大更新参数化（ μ P \mu P μP）类方法进行验证评估的最新研究成果

4. CerebrasGPT

本次讲座案例研究的重点将聚焦于三个代表性模型，分别是 Cerebras-GPT、MiniCPM 以及 DeepSeek：

接下来我们将重点解析 Cerebras-GPT、MiniCPM 和 DeepSeek 三大模型，这三个模型各自采用了差异显著的扩展策略组合，它们也将以不同方式向我们展示高效扩展的关键要素

首先我们要讨论的是 Cerebras-GPT 模型及其扩展方案：

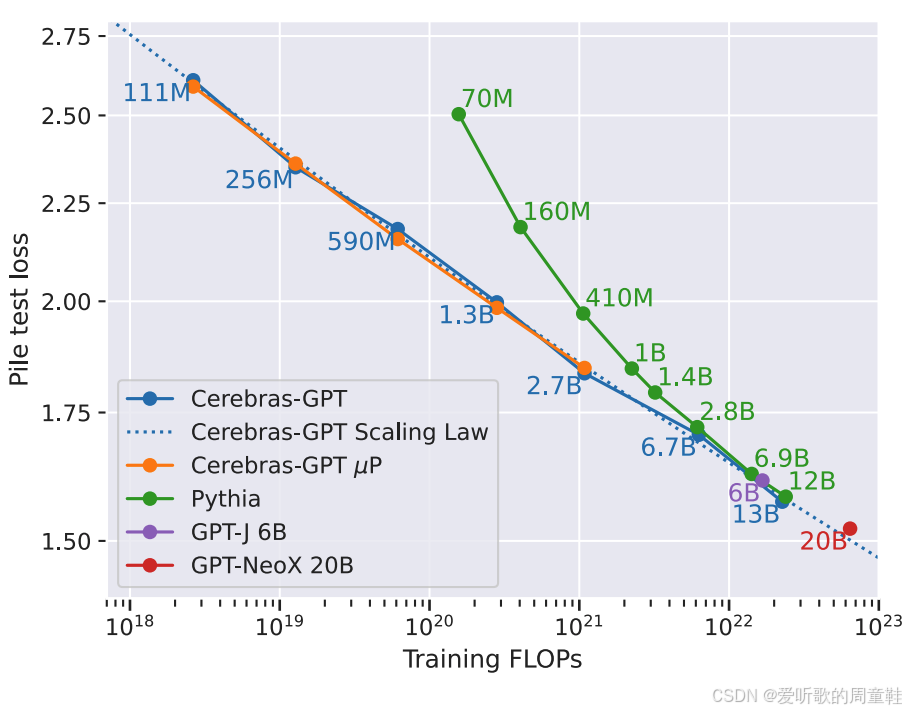
这是一个庞大的模型家族，该系列模型参数覆盖 1 亿至 130 亿区间，严格遵循 Chinchilla 训练方案，使训练 token 数量与参数规模保持最优比例关系，研究人员在其中发现了一个关键洞见，Cerebras 团队对这些缩放定律和参数化研究展现出浓厚兴趣，它们取得了一项极具价值的核心发现：通过扩展我们之前提到的最大更新参数化（ μ P \mu P μP）方法显著提升了模型扩展的稳定性和可控性

直接来看关键结论：上图展示了 Pile 测试集上的损失值，其中蓝色曲线就是 Cerebras-GPT 的扩展规律，橙色曲线标注了该模型在训练过程中采用了最大更新参数化方法，研究表明，该模型的扩展性表现优异---即便不优于 Pythia 和 GPT-J 等模型，至少也毫不逊色，这确实令人欣喜

这里要特别强调的是，这堪称是最大更新参数化（ μ P \mu P μP）的首批公开验证案例之一，众所周知，所有从事大语言模型扩展研究的实验，都会密切关注网络参数化方法和初始化策略，这些都需要根据模型规模进行动态调整。此外，诸如分层学习率等细节也是研究人员重点关注的要素，它们能显著提升模型扩展的稳定性，因此，像最大更新参数化（ μ P \mu P μP）这类方法在该领域具有相当重要的意义

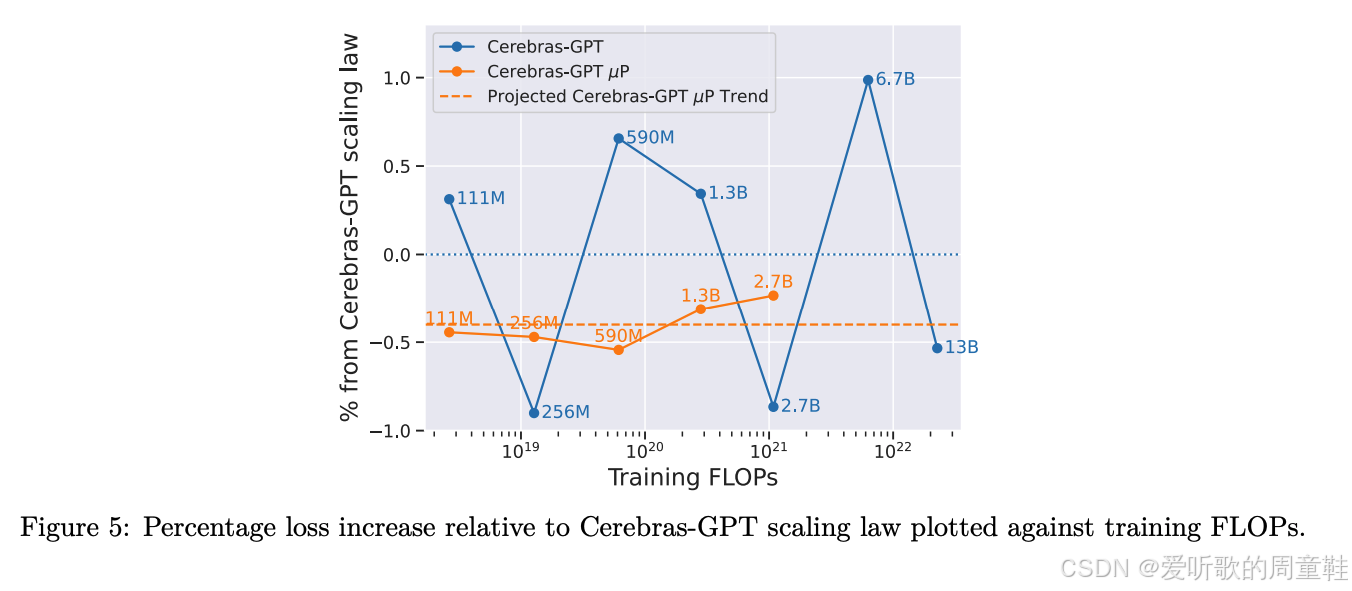
Cerebras 团队的研究表明：当采用标准参数化方法训练模型时，模型性能会在理论扩展点附近出现剧烈震荡，上图虚线所呈现的正是该现象，这种震荡现象源于一个关键因素---学习率必须根据模型规模进行动态调整，因此，他们很难完全精确地实现理论预测的性能表现，这正是图中虚线所代表的、基于现有扩展方案应达到的效果

但研究发现，当采用最大更新参数化（ μ P \mu P μP）方法时，模型性能会如橙色曲线所示，相比虚线方案，其表现与 μ P \mu P μP 版本的缩放定律预测值吻合度显著提升，因此他们的核心结论是：采用这种替代性参数化方法后，模型扩展行为变得高度可预测，超参数调优过程也显著简化，我们稍后将对此展开更深入的分析

Cerebras-GPT 团队及其他前沿研究机构发布的成果对实现最大更新参数化极具参考价值，这些研究在附录中提供了详尽的对照表格，清晰标注了标准初始化参数（SP）与最大更新化参数（ μ P \mu P μP）的具体差异：

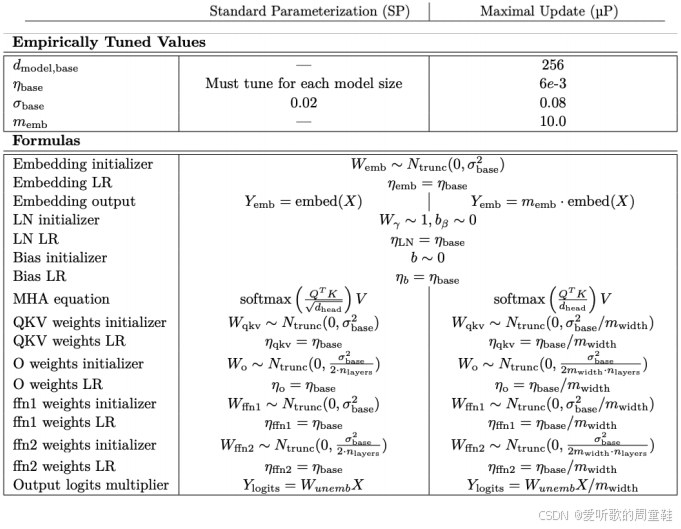
用一句话概况：基本上，所有非嵌入参数都以宽度的倒数作为初始值，而每一层的学习率则按宽度的倒数进行缩放 ，与标准参数化方法的关键差异在于---即便初始化阶段同样采用宽度倒数缩放，但其引入了分层差异化的学习率机制，这一点我们稍后会详细说明，我们将完整推导这个结果的数学过程，不过这里可以先看上面这个简明的速查表，若需具体实现，这套方法为 μ P \mu P μP 的实施提供了极其便捷的路径

另外一个值得注意的现象是，我们在其他缩放策略中也观察到了类似情况，可以将这些策略组合使用，比如将 μ P \mu P μP（它能确保超参数选择稳定性）与极具侵略性的缩放方案相结合。他们的做法是将实验规模逐级减小，直至模型参数降至 4000 万量级，他们在这个代理模型（proxy model）上进行了全面的超参数搜索，随后运用 μ P \mu P μP 方法将模型重新放大，在此过程中尽可能保持超参数的稳定性

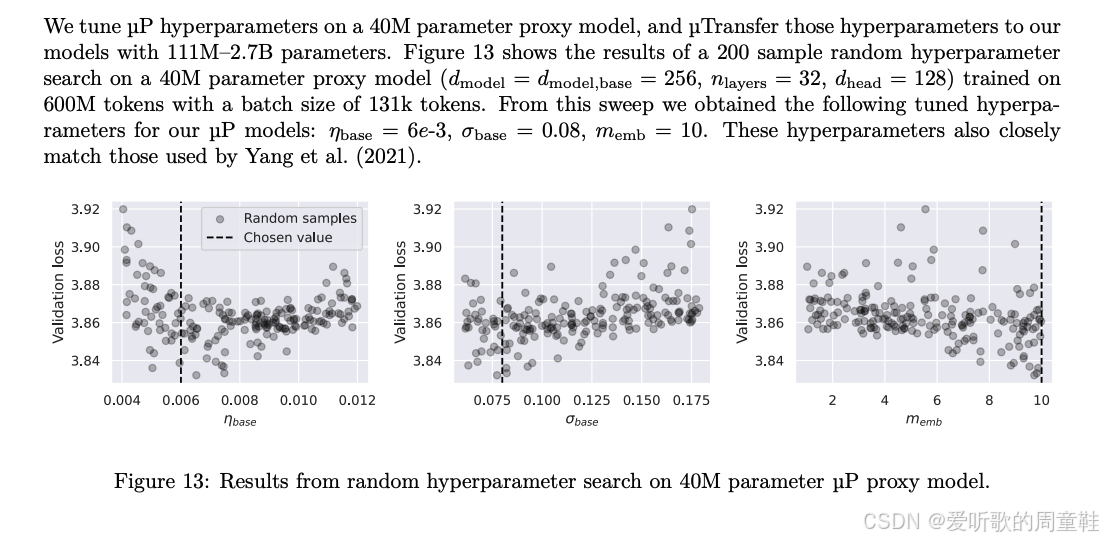
上图展示的是正是他们在小规模超参数搜索中观察到的现象，每个圆点代表一次模型训练过程，每个圆点都对应着一组特定的超参数，随后他们选取这些训练过程中的最优结果从而构建出完整的超参数网格。这种超参数选择方法非常清晰可靠，尚不确定这种激进的参数扩展方式是否真正适用于训练超大规模模型，不过这种策略在 MiniCPM 和 DeepSeek 等模型中也有体现---先训练较小的代理模型，再探索如何稳定地扩展至更大规模，这将成为贯穿始终的核心思路

5. MiniCPM

接下来我们讨论的另一篇论文是 MiniCPM，这是另一个典型案例，他们在模型缩放等领域做出了极具深度的探索

简单来说，他们的研究主要聚焦于通过大量计算资源训练出性能卓越的小型语言模型，为此，他们进行了大量精细的规模计算推演，他们再次采用最大更新参数化来稳定和简化扩展过程，不过这次扩展的不是模型规模，而是训练数据量

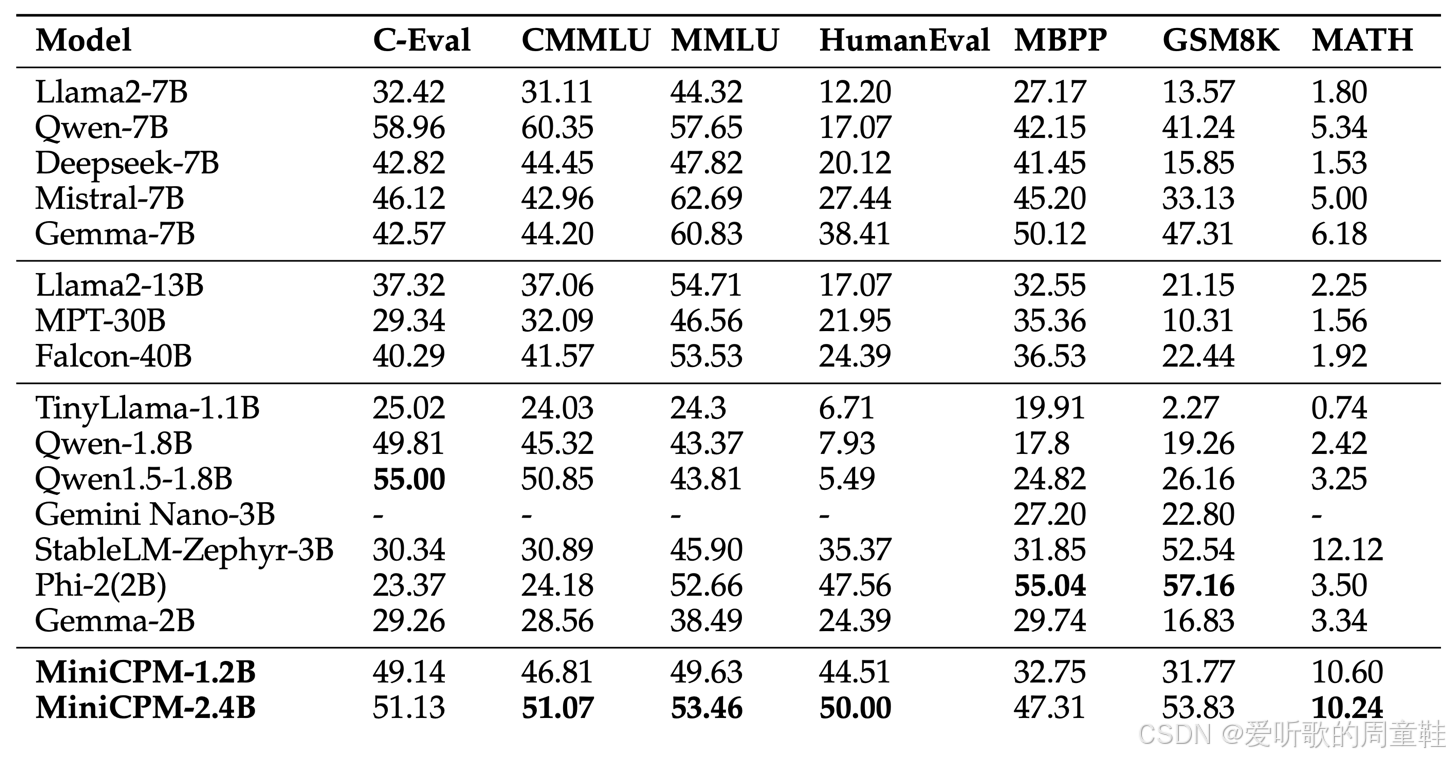
为说明这篇论文的参考价值需要特别指出：在当时训练条件下，他们研发的 12 亿至 24 亿参数模型展现出了突破性的性能表现，该模型性能超越了当时大多数 20 亿参数规模的模型，甚至能与 2024 年标准的 70 亿参数新模型相媲美

当然，如今（2025 年）我们已经能看到性能更优异的 70 亿参数模型，当这至少能让你感受到以 2024 年年中可用的算力与技术条件而言，这个模型确实代表了当前的最前沿水平，他们确实掌握了关键技术，才能打造出如此高质量的模型

正如 Cerebras-GPT 所展示的，关键在于必须制定正确的缩放策略，现在退一步看，当你准备进行大规模模型训练时，关键步骤在于必须精心选择超参数，必须确保这些超参数具备良好的可扩展性才能顺利实现模型规模的升级

5.1 Techique 1: muP to stabilize scaling

我们可以采用与 Cerebras-GPT 团队相同的实现方案，我们可以先在较小规模下选定超参数，确保其稳定性后再逐步扩展整体规模，实现这一目标的有效方法就是采用类似最大更新参数化（ μ P \mu P μP）的方案

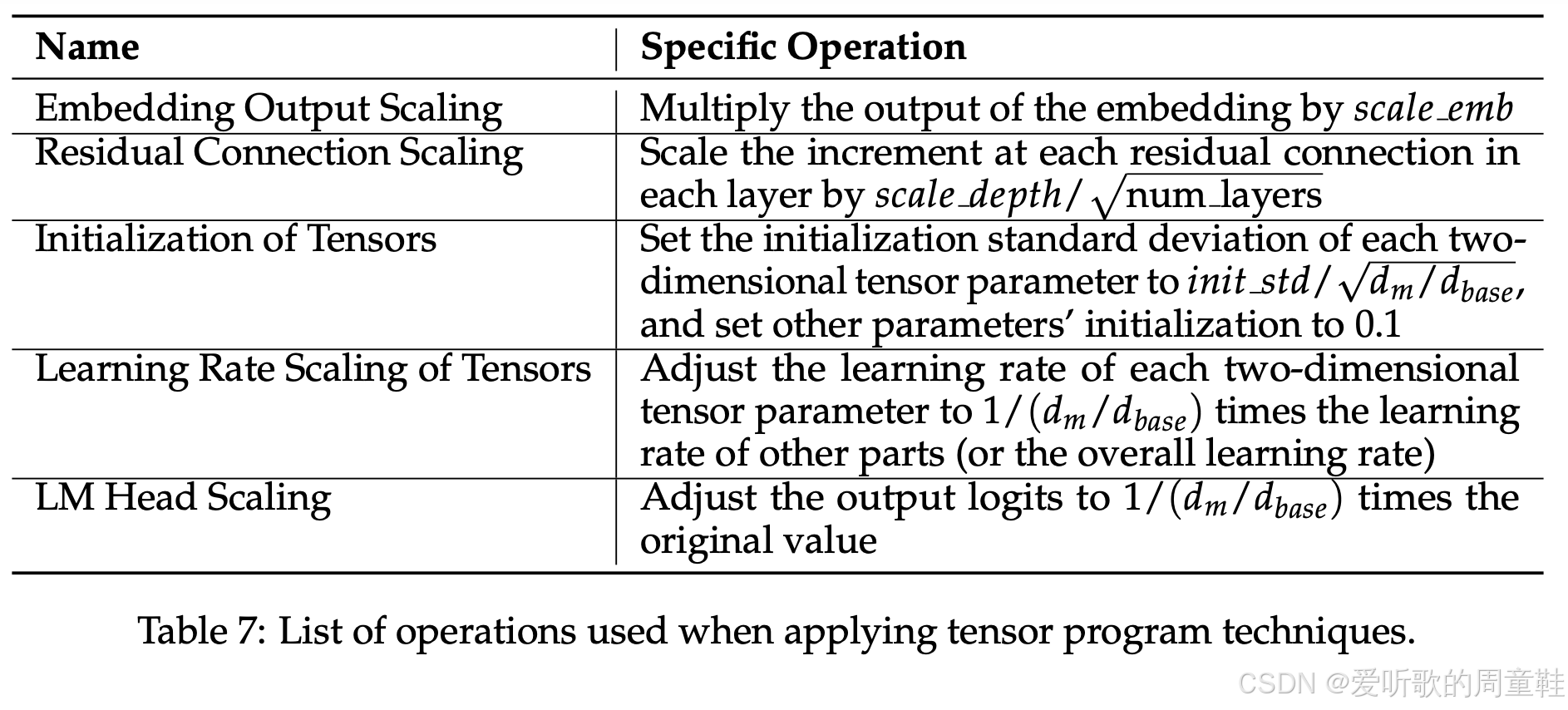
可以看到，这里采用的策略完全如出一辙，对于嵌入层，实际上无需特殊处理，只需按常数比例进行缩放即可，当遇到类似多层感知机（MLP）这样的残差连接结构时，只需将其缩放为层数的平方根倍，即乘以 1 / num_layers 1/\sqrt{\text{num\_layers}} 1/num_layers ，其中 num_layers 为层数，初始化时采用其宽度的倒数作为缩放因子，而模型的学习率则需根据网络宽度进行同步缩放

这与 Cerebras-GPT 案例中采用的策略完全一致，相同的缩放因子规律在此重现，最终获得的超参数与 Cerebras-GPT 高度吻合：词嵌入维度采用相同量级，学习率数值仅存在约两倍左右的细微差异，但总体而言，这些超参数的最终取值区间基本趋同，此时只需确保最优学习率保持稳定即可推进后续流程

我们深知模型宽深比（aspect ratio）至关重要，因此在确定最佳比例后便将其固定下来，随后将模型规模从 900 万或 3000 万参数逐步扩展，直至构建 5 亿至 10 亿参数量级的大型模型，他们实现了约 5 倍甚至更高的计算效率提升，从最小规模模型到最大试验模型

5.2 Optimal batch size and LR

现在，你可以使用这种方法来验证 batch 大小是否随模型规模实现了最优配置，准确来说，关键批量大小（B_crit）本质上对应着收益递减的临界点，随着模型规模扩大，其损失值会相应降低，当损失值降低时，便可逐步采用更大的 batch size，关键批量大小本质上反映了当前模型规模与计算条件下的最优操作区间

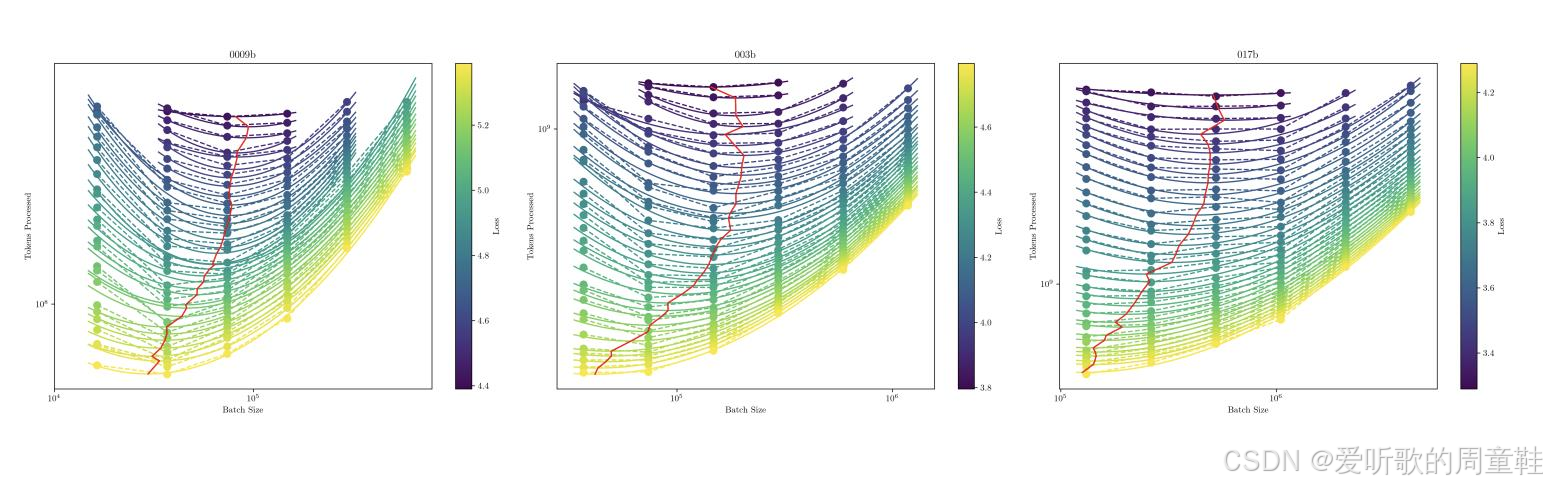
当前模型训练应采用的最优全局 batch size 是多少呢？与 Kaplan 论文所述方法类似，这些研究遵循了相同的技术路线，虽然曲线形态与 Kaplan 论文呈现不同，但底层策略一脉相承，他们试图探究的是不同模型训练时的关键 batch size 或最优 batch size，他们致力于揭示 batch size 与数据量/损失值之间可预测的缩放规律

图中纵列代表单条训练曲线，随后通过拟合二次曲线来定位最小值，图中红线代表随着训练进程推进，所有数据点中的最优值轨迹，这表明在特定模型规模与数据集大小的组合下，最优 batch size 的确定方法可沿用 Kaplan 论文中的逻辑框架来确定

若你还记得 Kaplan 的论文以及之前课程讨论的关键 batch size 的相关内容，你应该记得最具可预测性的其实是训练目标损失值（即最终损失）以及关键 batch size 的临界点

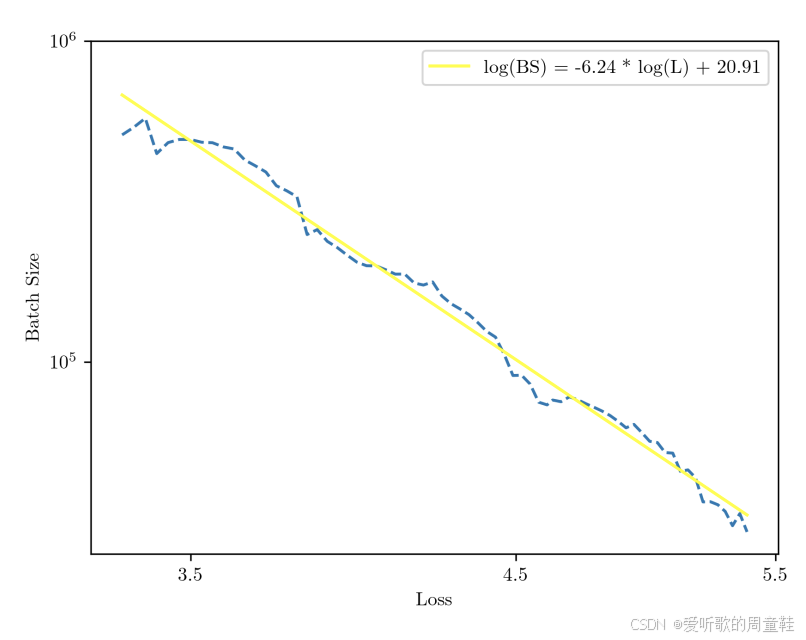
正如 Kaplan 研究中所示，我们再次观察到目标损失与理想 batch size 之间呈现对数线性关系，由此便可推算出应采用的 batch size 。只需确定目标计算量级，就能通过缩放定律预估预期能达到的损失值，一旦确定了预期损失值即可反向推导出可操作的 batch size，这里存在一个清晰的趋势：随着损失值降低，batch size 呈多项式增长

需要注意的是，batch size 会随着目标损失值进而计算量的变化而动态调整，因此我们需要为此拟合一个缩放定律，但我们已完成了最大更新参数化，理论上，若该方法有效，此时我们应能观察到最优学习率趋于稳定

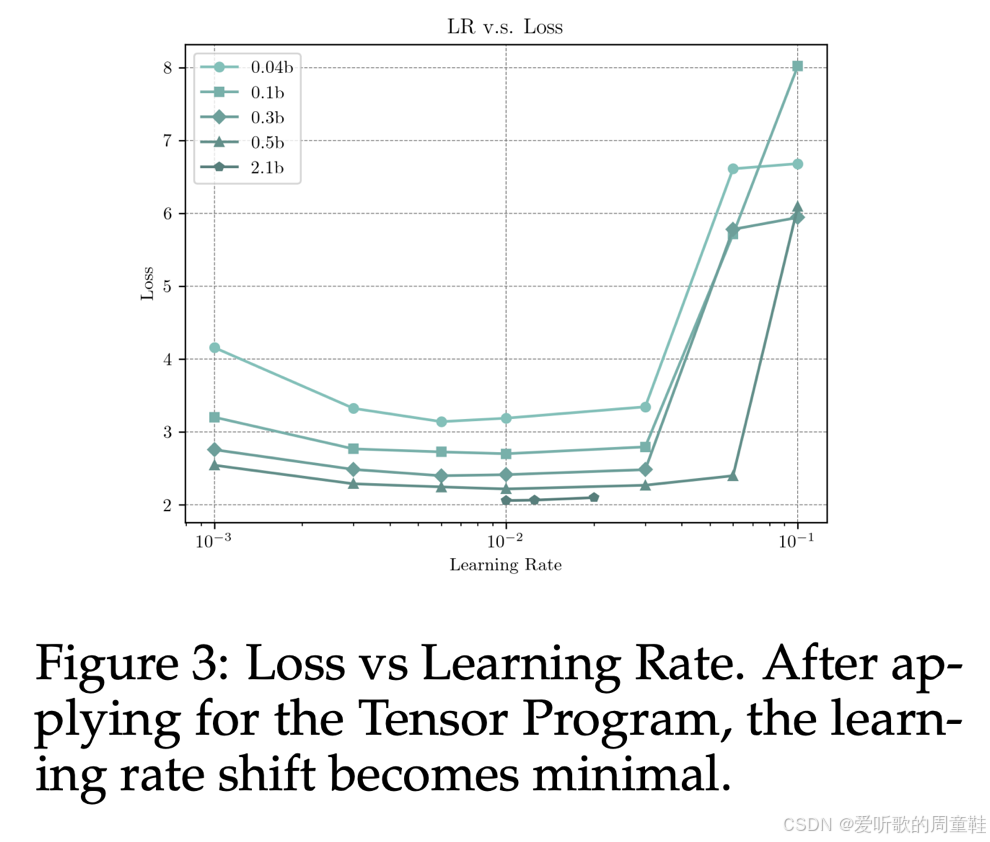
在上面这张图表中，我们实际上看到的是不同规模的模型，从浅色标注的小型模型到深色标注的大型模型，图中展示了不同学习率的变化情况，由于计算资源限制，大新模型仅运行了较短时间，但可以观察到相当明显的趋势，这与 Kaplan 等人早期研究结果高度吻合：模型性能存在一个相对宽阔的稳定区间，而当超出该区间时，模型不稳定性会急剧上升，但关键在于这个最小值在多个数量级范围内保持稳定，从小型模型到大型模型，最优学习率始终稳定在 10^-2 附近

这一发现提供了有力佐证：通过正确缩放模型初始参数和各层学习率，我们无需反复调整学习率，甚至不必依赖学习率缩放定律来预测最优值，系统已自动实现最优配置

5.3 What remains -- model size vs data tradeoffs

最后需要考虑的是模型规模与训练数据量的最佳配比关系，训练小型模型时，很可能会出现训练过度的情况，开发者甚至需要明确使用海量训练数据的合理性，此时可以参考 Chinchilla 论文的分析方法进行验证

MiniCPM 团队实现了一项极具创新性的突破，虽然类似方法早有先例，但他们首次在 LLM 领域（尤其是遵循 Chinchilla 范式时）实现了这一技术的规模化应用推广

缩放的核心原则如下：假设我们需要拟合 Chinchilla 缩放定律，具体实现时需要执行哪些步骤？需要同时调整训练数据量（token 数量）和模型参数量两个变量，具体操作时，先固定模型参数量，然后逐步延长训练周期，理想情况下，可以通过早停机制获取不同训练阶段的检查点，这些检查点实质上就对应了不同规模的数据集训练效果

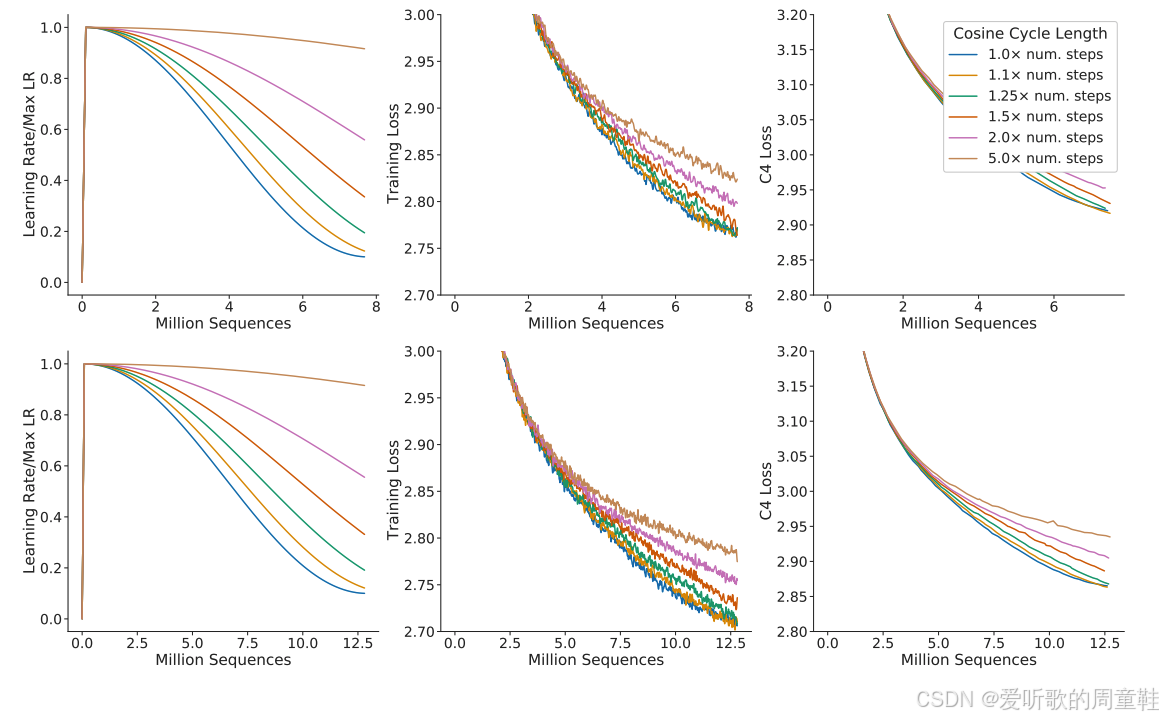
由于早期检查点接触的数据量较少，单次训练运行就采集到完整的数据规模变化规律，将大幅提升实验效率。遗憾的是，如上图所示，针对不同数据量目标所对应的余弦学习率曲线存在显著差异，当训练数据量极小时，余弦学习率曲线会呈现特殊形态，预热阶段保持常规节奏，但冷却阶段的下降速度会显著加快，训练时长大幅缩短后，学习率就会急速下降，而当数据量充足时，学习率会以平缓的节奏逐渐收敛至训练终点

因此，小规模数据训练与大规模数据训练所采用的学习率策略必然存在差异，这一点至关重要。许多人都在这个问题上栽过跟头，绝不能仅凭单次余弦学习率模型的运行结果就试图通过早期检查点来推理数据规模对模型的影响规律。要避免这个问题，通常需要从头开始训练多个模型，每个模型都训练至不同的终止点，必须针对每个目标终点单独进行完整训练，这样一来，所需的训练次数就变成了 n^2 量级

虽然部分训练规模较小，但本质上需要进行大量独立训练，每个终止点都需要单独训练，而不能通过单次训练收集检查点来实现，这种操作方式显然违背常理

5.4 (partial) solution in miniCPM -- WSD learning rate

MiniCPM 团队提出的 预热-稳定-衰减（WSD）学习率调度策略 因此广受关注：

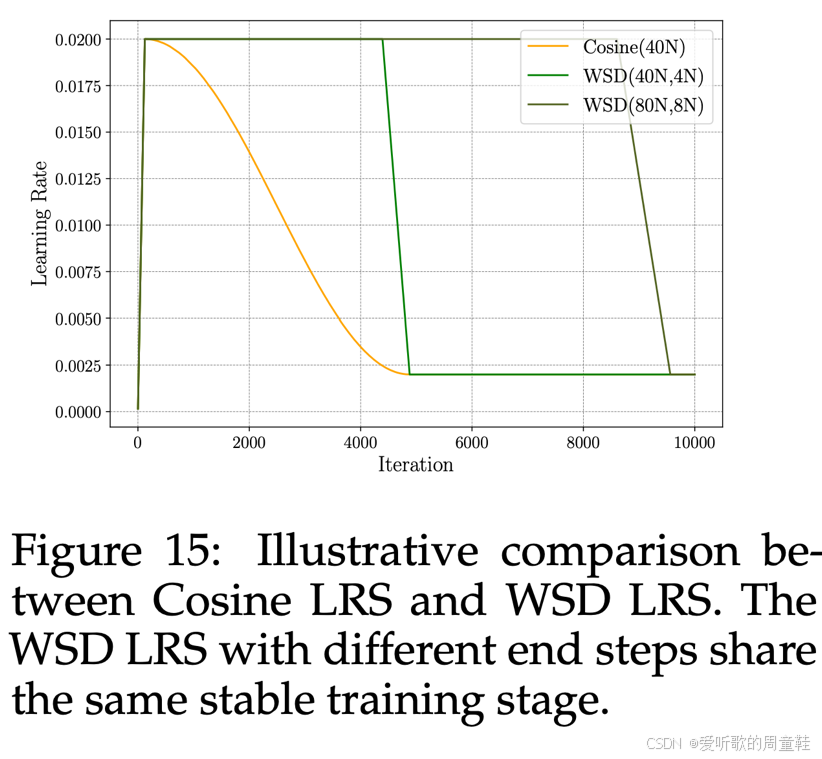
上面这张图表清晰地揭示了其中的运行机制，我们通常采用的训练方法是这张黄色曲线所示的余弦学习率，学习率首先上升，经过一个通常很短暂的预热阶段后，学习率会达到峰值，随后遵循余弦曲线逐渐衰减至终止点，最终可能维持在最低学习率水平

当然，这些设置都是可选的，你可以选择在某个地方终止训练，也可以选择将学习率一直衰减至零，因此，余弦学习率的变化曲线呈现如图的形态。当然，这里的问题在于：如果设定不同的目标值，余弦曲线就会完全改变形态，因此，预热阶段之后的所有训练过程都无法复用

现在来看这种新型的预热-稳定-衰减（WSD）学习率调度策略，本质上是一种梯形学习率曲线，它包含三个典型阶段：其预热阶段与余弦调度完全一致，随后进入平稳阶段（学习率保持恒定），最后通过衰减阶段将学习率降至预设最小值。当然，这种调度方式可以衍生出多种变体，你可以先升后降，最终稳定在最低学习率，这些变体组合都可以自由搭配使用，不过最基本的形式还是预热-稳定-衰减-终止这个经典流程

这种设计有何优势呢？这种设计的优势在于可以复用稳定阶段，具体操作是这样的：如果想在单次训练中近似实现 Chinchilla 的效果，可以采用预热-全程稳定运行-冷却的调度策略，这时如果想评估 "如果减少训练数据模型表现会如何" 只需回滚检查点重新执行冷却阶段即可，这样就能在不从头训练的情况下，精确复现预热-稳定-衰减的学习率曲线

这种设计确实非常巧妙，关键在于稳定阶段的学习率保持恒定，这使得我们能够以单次训练或接近单次训练的成本实现 Chinchilla 风格的数据扩展或模型缩放，如今这种方法已被广泛采用

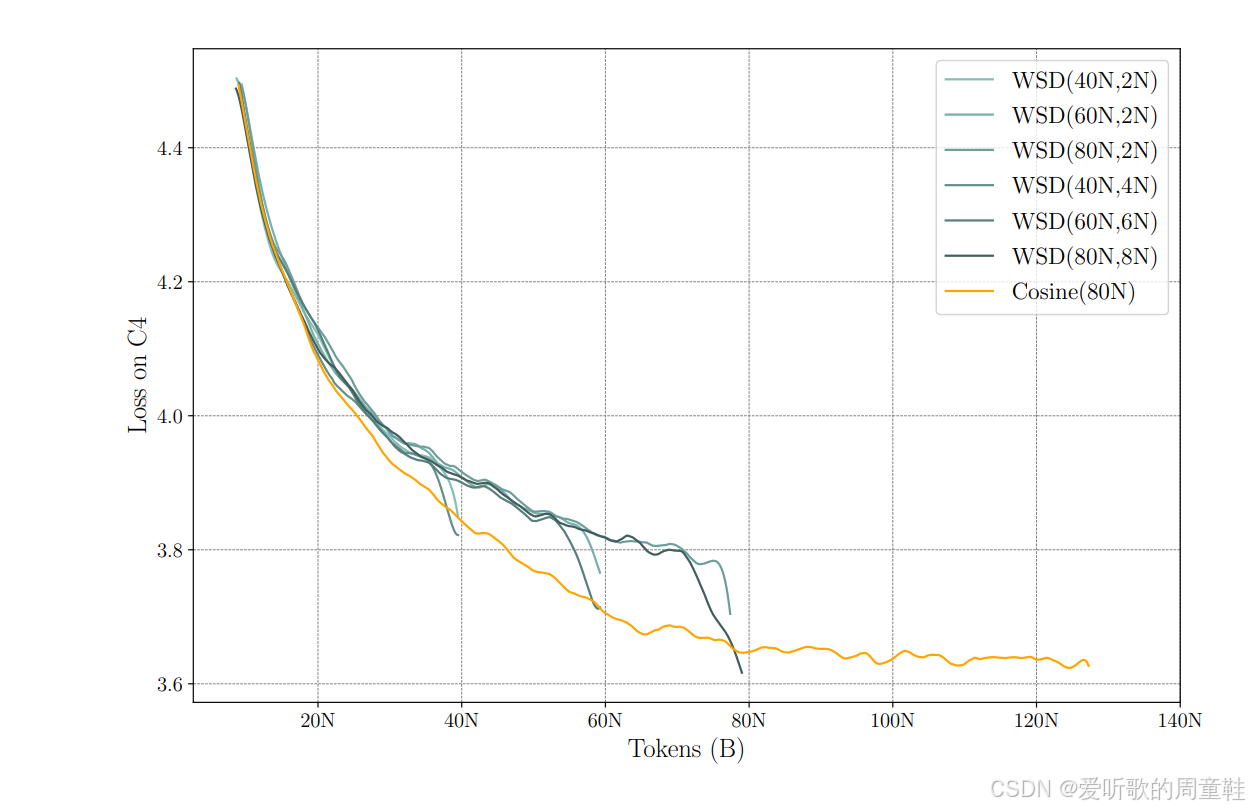
如上图所示，若采用余弦学习率调度，你会观察到损失值沿着图中这条黄色呈现相对可预测的平滑衰减趋势，最终收敛至目标值。若采用预热-稳定-衰减策略训练，你将观察到更为复杂的损失曲线形态，其波动特征明显区别于常规模式

正如图中这些深色线条所示，训练曲线中并未明显体现的预热阶段，随后进入稳定阶段，此时学习率正常下降，而当进入衰减阶段（即冷却期）时，损失值会急剧下降，直至学习率降至零点或最低预设值，此时便达到了最终损失值，这些看似异常波动的损失值曲线，实际上在使用快速冷却学习率策略训练时是完全正常的现象

这里的关键发现是：在每一个 token 数量级上，预热-稳定-衰减学习率曲线的最低点都优于或等同于余弦学习率的表现。但这并非绝对规律，有时余弦学习率效果更佳，有时预热-稳定-衰减（WSD）策略更具优势，但总体而言，业界普遍认为这两种学习策略效果相当。不过 WSD 方案还有个显著优势，那就是无需纠结训练终止时机的选择，你可以通过多次冷却过程，轻松获取不同数量级的检查点

5.5 Side note -- other ways of estimating chinchilla curves

当然，业界还涌现了其他用于估算 Chinchilla 缩放曲线的方法，华盛顿大学与苹果公司的研究团队曾联合发表论文，专门探讨 Chinchilla 惩罚项的估算方法，当你持续增加数据量时，其损失值会比按照 Chinchilla 缩放定律计算的结果恶化多少呢？

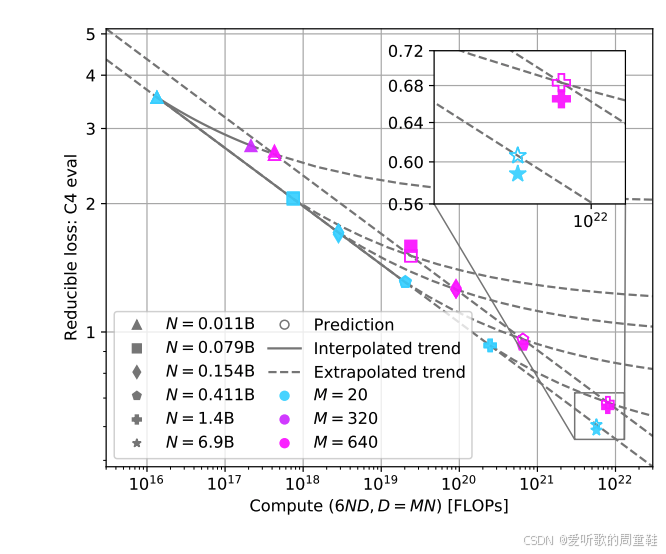
如图所示，图中这条蓝绿色曲线代表模型参数与训练 token 数的比例为 1:20，那么我们可以思考：如果将训练 token 数与参数的比例调整到 320:1 会产生怎样的效果？此时会出现一条与之平行的独立缩放曲线，此外还有另一条曲线（圆形标记），代表 640:1 的训练比例，图中颜色较深的那条就是

他们实际揭示的是：与其采用这种 WSB（权重共享绑定）风格的做法，另一种可行方案是尝试量化模型性能随 token 与参数量比值升高而下降的程度。事实证明，这种变化规律同样呈现出相当可预测的形态，通过观察小规模训练时的性能衰减趋势，我们就能推演出这种规律

目前尚未出现基于这一理念开展的大规模训练实践，但令人振奋的是，通过在小规模训练中推算访问 token 惩罚的规律，理论上几乎只需一次训练就能实现 Chinchilla 级别的效果

5.6 Chinchilla-type analysis

回到 MiniCPM 的话题，现在，我们已掌握所需的关键工具，我们拥有 WSB 学习率这项关键技术，通过单次训练，我们就能在训练过程中动态调整数据配比，通过针对不同模型规模进行多轮训练，我们已具备开展 Chinchilla 分析所需的全部条件，他们采用了 method 1 和 method 3---如果你还记得这两种方法的话

方法 1（method 1）是将所有学习曲线叠加后，取其下包络线，所有训练曲线的下包络线理论上应近似呈现幂律分布，而方法 3（method 3）则是通过联合拟合上图中列出的方程 (2)，即假设这个双变量缩放定律，并以曲线拟合的方式将其适配到所有可用数据上，通过该拟合结果，我们就能求解出最优的 token 与数据比例，因此他们同时采用了这两种方法

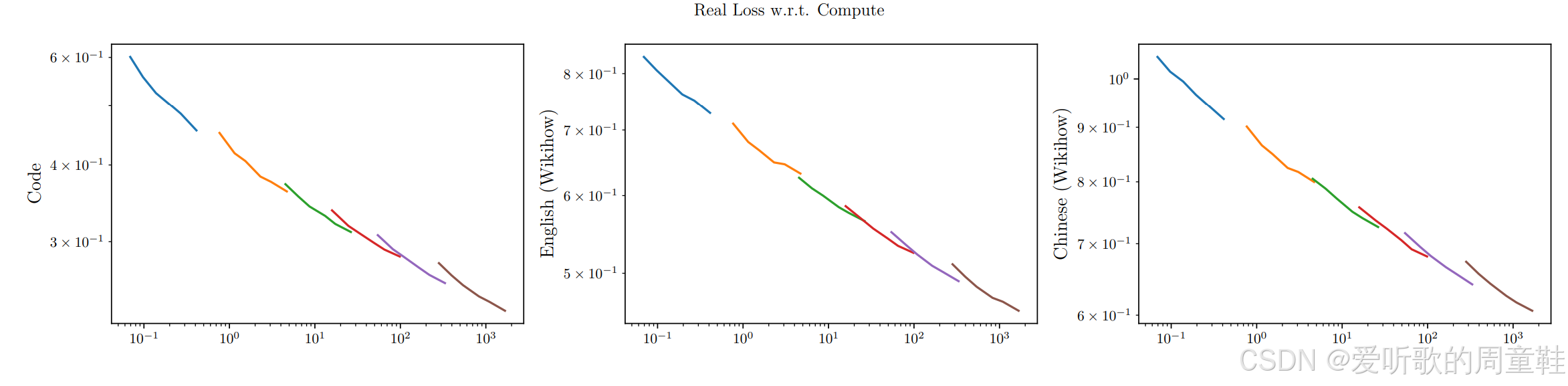
在 Chinchilla 研究中，方法 1 确实呈现出较为明显的趋势，尽管并非完全线性，这使他们能够从计算量推导出 token 比例，

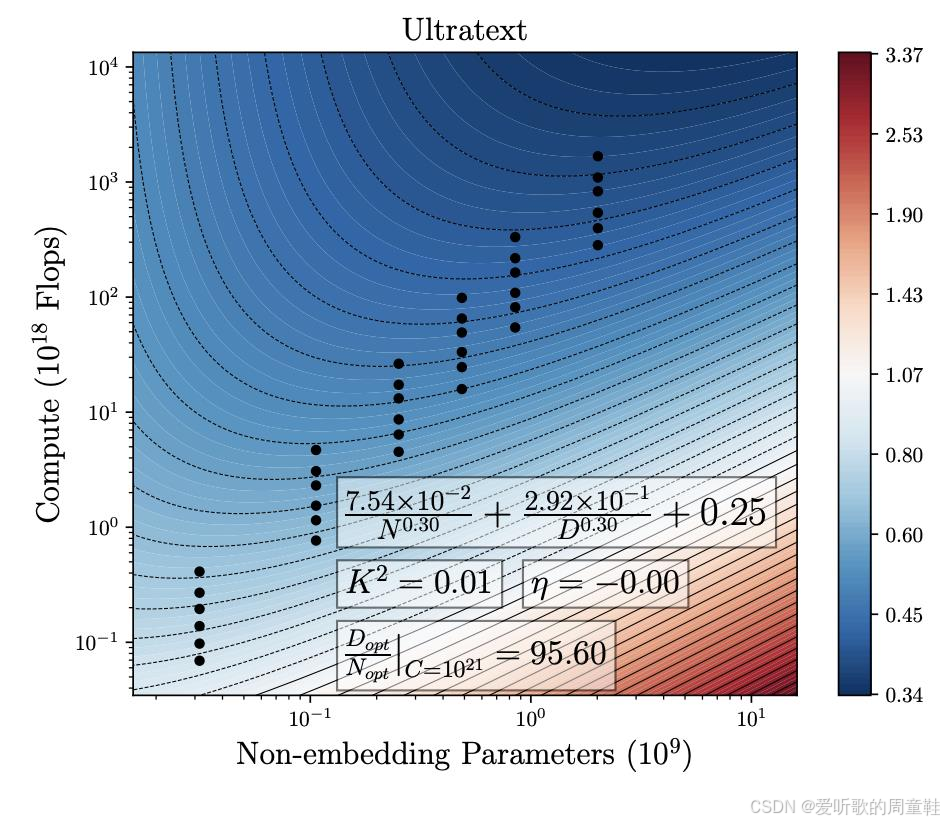
他们用于论证多数设计决策的主要依据正是方法 3，核心在于曲线拟合，你在上图中看到的等高线，正是他们所拟合的曲线，图中这些散点代表他们为拟合 Chinchilla 参数所进行的小规模实验运行，为验证其方法的合理性，他们得出了极高的 token 与参数比例，这个数值（192）看起来完全是个异常值，这个结果与现有的大多数文献数据并不十分吻合

他们认为，由于数据质量的提升和模型效率的改进，Llama 架构的模型都应具有更高的 token 与参数比例，但其估算的这个比例数值确实高得异乎寻常，192 个 token 对应 1 个参数，这个比例推导结果从未在其他研究中见到过，但不可否认的是，我们确实观察到 Llama 3 等最新模型的数据与参数比例显著提升，同时，我们并未观察到明显的收益递减现象，这些模型的性能表现并不逊色于采用 Chinchilla 缩放标准的 Llama 2 同级别模型

这表明，通过精细化的优化与调参，我们完全有可能突破 20 倍模型规模的经验法则限制，最关键的启示或许不在于是否采信 MiniCPM 采用的特定缩放定律，而是认识到 Chinchilla 分析实际上并不构成严格限制，20 倍模型规模仅是个起点，开发者完全可用大幅提升 token 与参数的配比

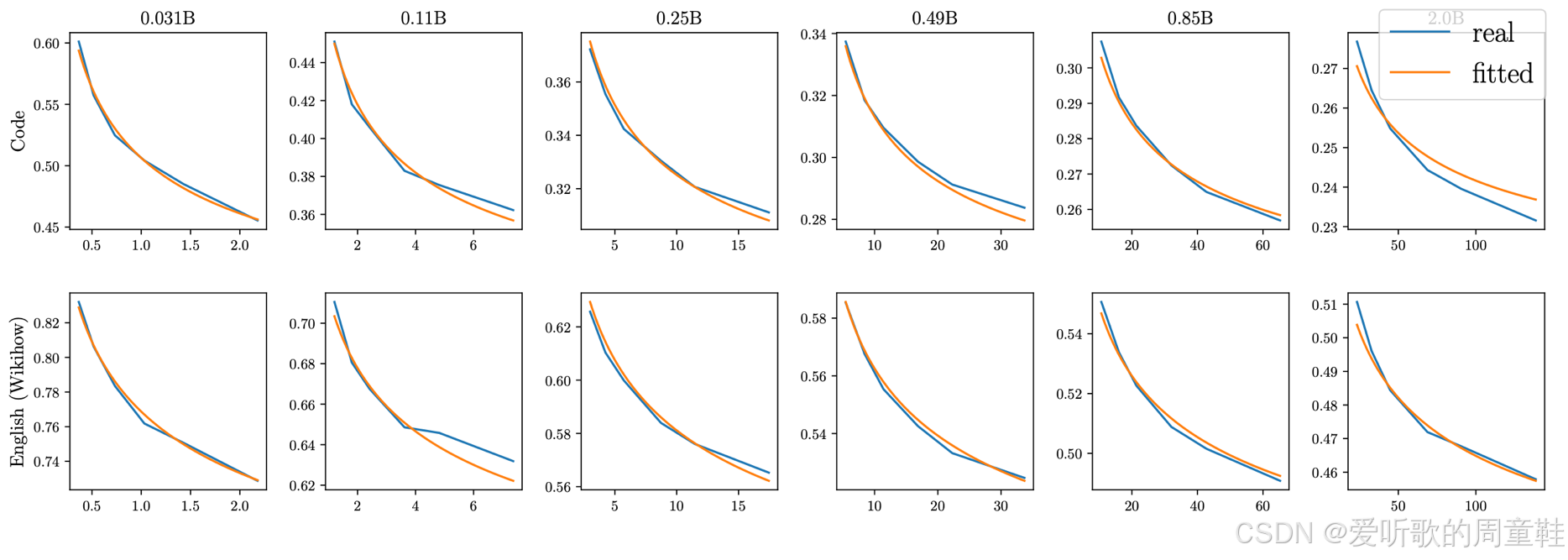
最终，他们获得的拟合曲线整体呈现出相当理想的状态，上面这张曲线图展示了代码与英语文本在数据规模、模型尺寸与困惑度之间的缩放定律关系，虽然拟合效果整体良好，但确实存在一些难以解释的异常数据点，但随着数据量的增加，这些相对小规模模型所拟合出的缩放定律整体表现相当出色

这是大规模训练任务中一个典型的参数缩放方案实例，我们就讲到这里

6. DeepSeek

接下来想讨论的另一篇论文来自 DeepSeek 团队

这是 DeepSeek 团队 2024 年发布的奠基性大语言模型论文，研读 DeepSeek 原始论文时，你会明显感受到团队严谨的科研态度，他们通过大量精细的规模化消融实验，在模型扩展过程中力求每个环节的精确把控，这种精益求精的态度，正是那些成功实现模型扩展的研究团队共同秉持的核心理念

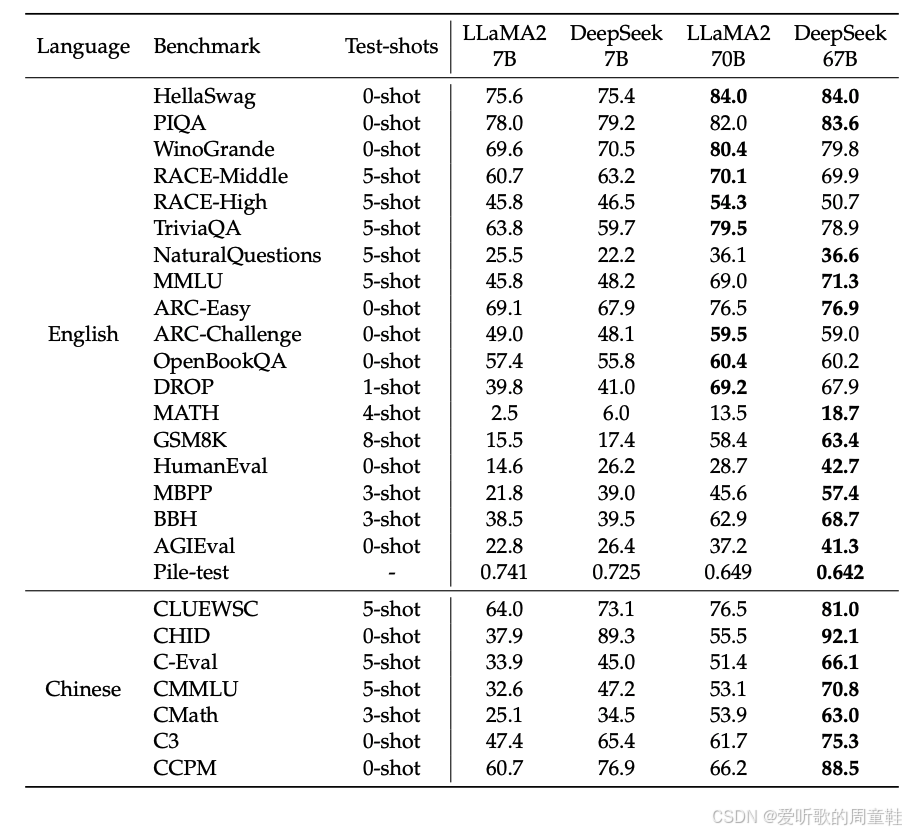
他们构建了 70 亿与 670 亿参数的双模型架构，在当时，这些模型的性能显著超越同期主要竞品 Llama 系列，当时 Llama 2 和 Mistral 占据主导地位，而 DeepSeek 横空出世，实现了与之比肩的性能表现，虽不似 DeepSeek-V3 对决 OpenAI GPT-4.0 时那般惊艳全场，但作为首次尝试，这样的成果已堪称惊艳，那么让我们深入剖析其中的技术原理，DeepSeek 究竟做对了什么，才能从零起步一跃成为当时开源领域的顶尖水平的

在众多研究团队中，DeepSeek（或许唯一可比的是 MiniCPM）对实验细节和超参数选择方法的公开程度堪称典范，他们近乎透明地披露了大量研究过程

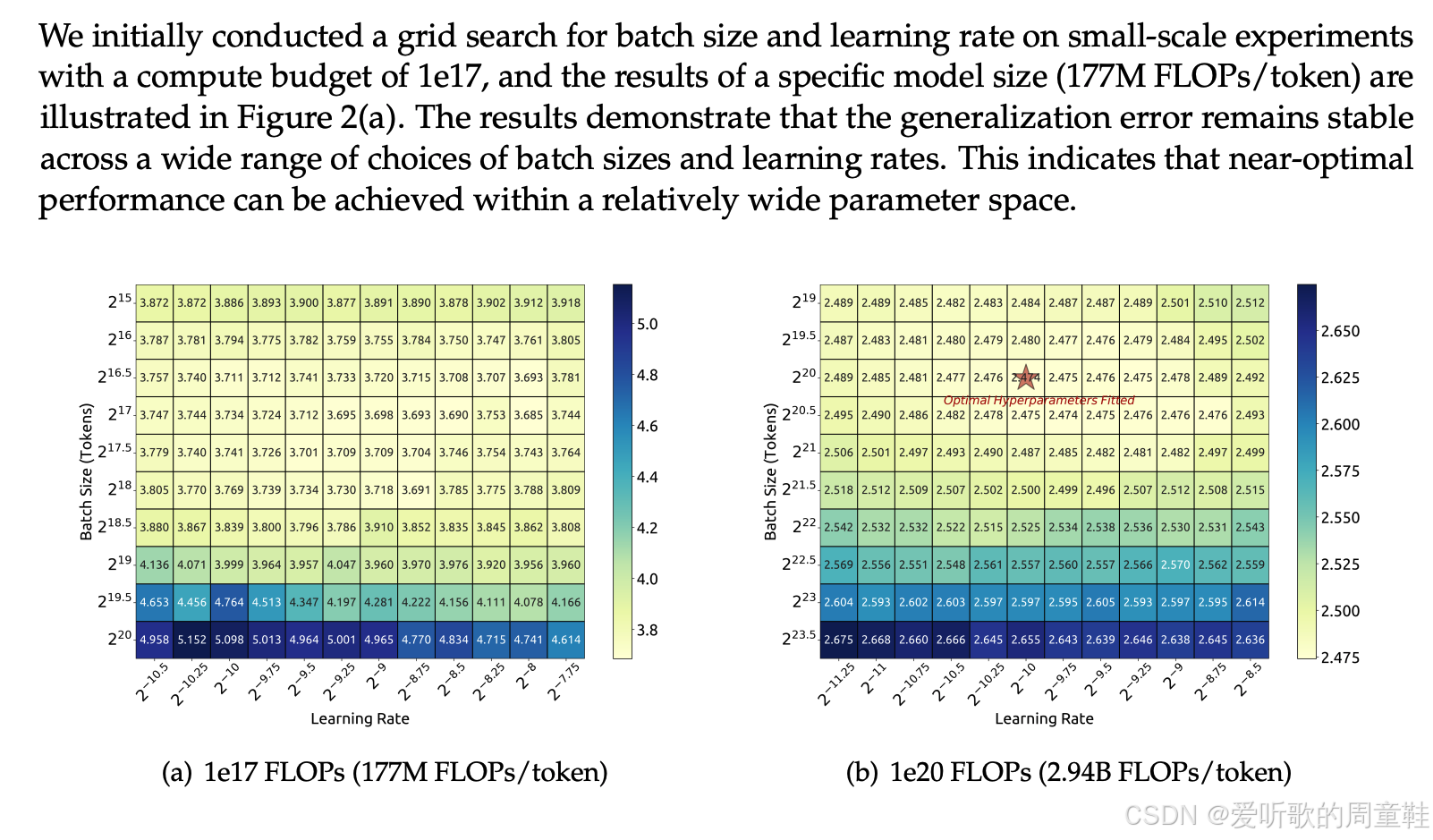
这里我们立刻能看到 DeepSeek-V1 与 MiniCPM 以及 Cerebras-GPT 的关键差异：前者完全未采用 μ P \mu P μP 参数化方法，他们决定直接通过实验同步测算最优 batch size 与最佳学习率，这堪称一种极其直截了当的研究方法，当然，其背后必须对缩放定律怀有坚定不移的信念

他们的具体做法是：选取两个相对较到的模型，分别在多个 batch size 和学习率参数组合上进行网格搜索，最终获得不同参数配置下的损失值分布，随后，他们以更大规模重复了相同的实验流程，通过这种方法，就能确定最优 batch 和学习率，因此他们得出的结论是：这个参数优化空间相当宽广，实际操作中无需过分担心参数配置失误的问题

基于这一认知，他们采取了以下策略：虽然学习率和 batch size 的选择都具有较大容错空间，但仍需确保这两个参数的数值量级准确无误，那么如何确保这些参数的数值量级准确呢？具体操作方法是：我们将训练一系列具有不同非嵌入计算量的模型，通过网格搜索的方式系统调整之前提到的两个关键参数即 batch size 和学习率，通过这种参数组合实验，我们就能确定在不同计算规模下对应的最优 batch size 与最优学习率

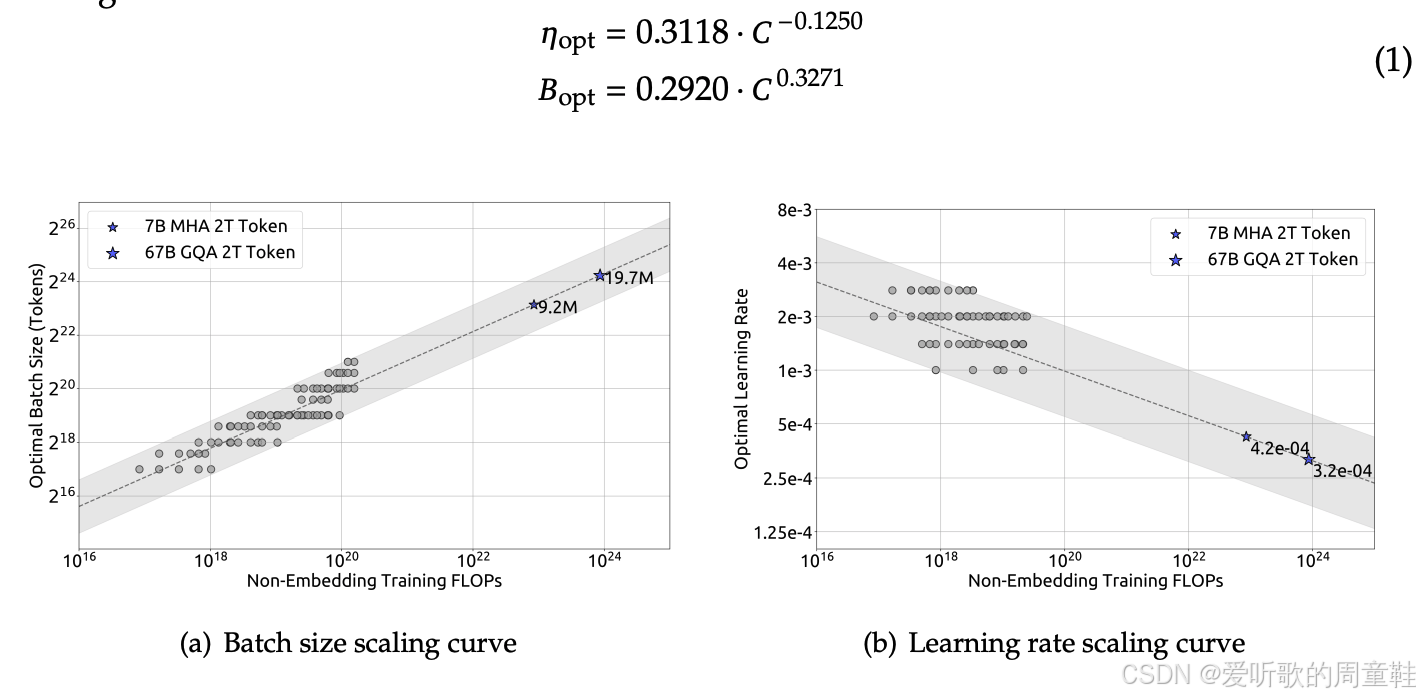
可以想象，我们会在不同计算量（FLOPs）规模下建立前面那样的参数网格，并为每个网格点标注最优配置（用星号标记），正如这个关于缩放定律的讲座所预示的那样，这些参数关系显然遵循着缩放定律的线性规律，至少在 batch size 方面，这种规律性表现尤为明显，通过拟合趋势线，我们就能推算出训练更大模型时所需的最优 batch，同样的方法也适用于学习率的优化，他们拟合出趋势线后，就能确定我们要采用的最优学习率

而当时，他们也确实遵循了行业的最佳实践，他们采用了 Chinchilla 式的参数分析，他们再次采用了 WSD 风格的学习率设定方法，本质上是为了最大限度地减少重复计算的工作量

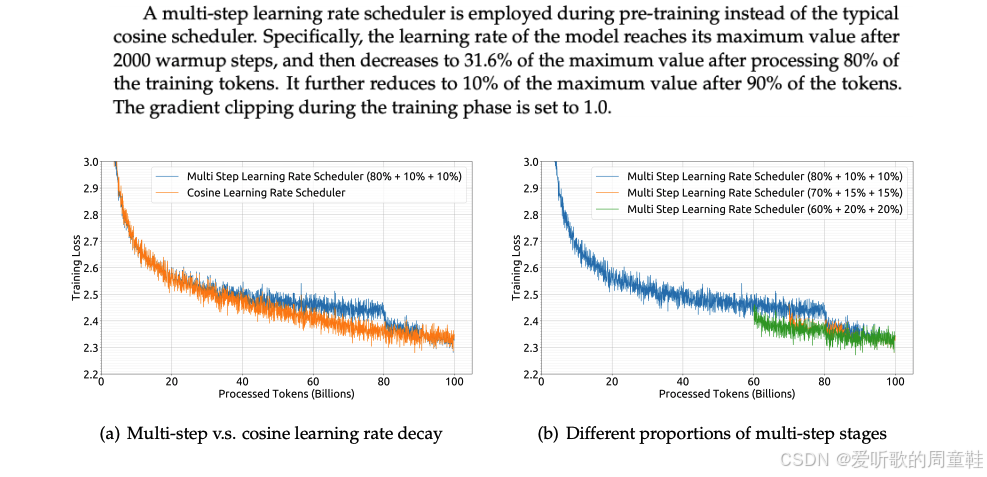
他们的做法有些特别，甚至可以说不太常规：先进行预热进入稳定阶段后，接着执行两组衰减步骤，最终将学习率逐步衰减至 0，整个衰减过程分为两个阶段，每个阶段占 10% 的训练时长，他们对这种衰减阶段的不同设置方案进行了对比分析，但分析结果显示，这种设置差异对最终效果的影响并不显著，但总体而言，约 20% 的总计算资源会被分配到这个冷却阶段

他们的研究再次证实，这种设置与余弦学习率衰减的效果相吻合，但这种方法的最大优势在于，我们能够以极低的成本完成 Chinchilla 风格的分析

相较于学习率拟合，Chinchilla 风格的分析呈现出极其清晰、规整的拟合效果，这是一个具有普适性的重要经验，观察众多研究者提出的缩放定律时，关于超参数的部分往往显得较为杂乱且缺乏说服力，但所有研究团队进行的等计算量分析，其结果始终呈现出高度一致且完美的规律性

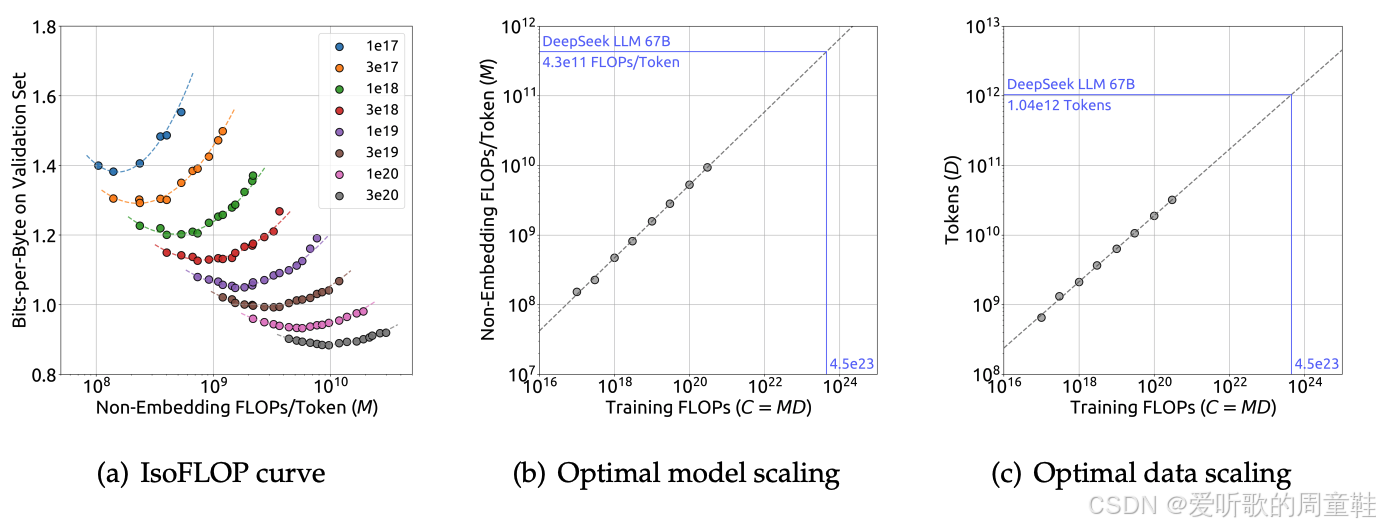
上图展示的正是对 Chinchilla 研究成果的完美复现，可以看到不同的计算规模我们观察到不同的二次函数关系，我们沿着这些二次曲线的底部绘制了一条趋势线，我们精确得出了最优解，准确地说，是作为训练计算量函数的最优每 token 计算量（FLOPs/Token）与最优 token 规模，这为我们提供了一种直观的方法来分析 token 规模与模型规模之间的取舍关系，这使他们能够从头开始完成所有工作

值得一提的是，他们重新开展大量这类研究确实很有价值，他们本可以照搬 Chinchilla 的做法，直接采用 20 个 token 对应 1 个参数的比例，但他们选择另辟蹊径，实际进行缩放定律分析，确保 token 规模与自身需求相匹配

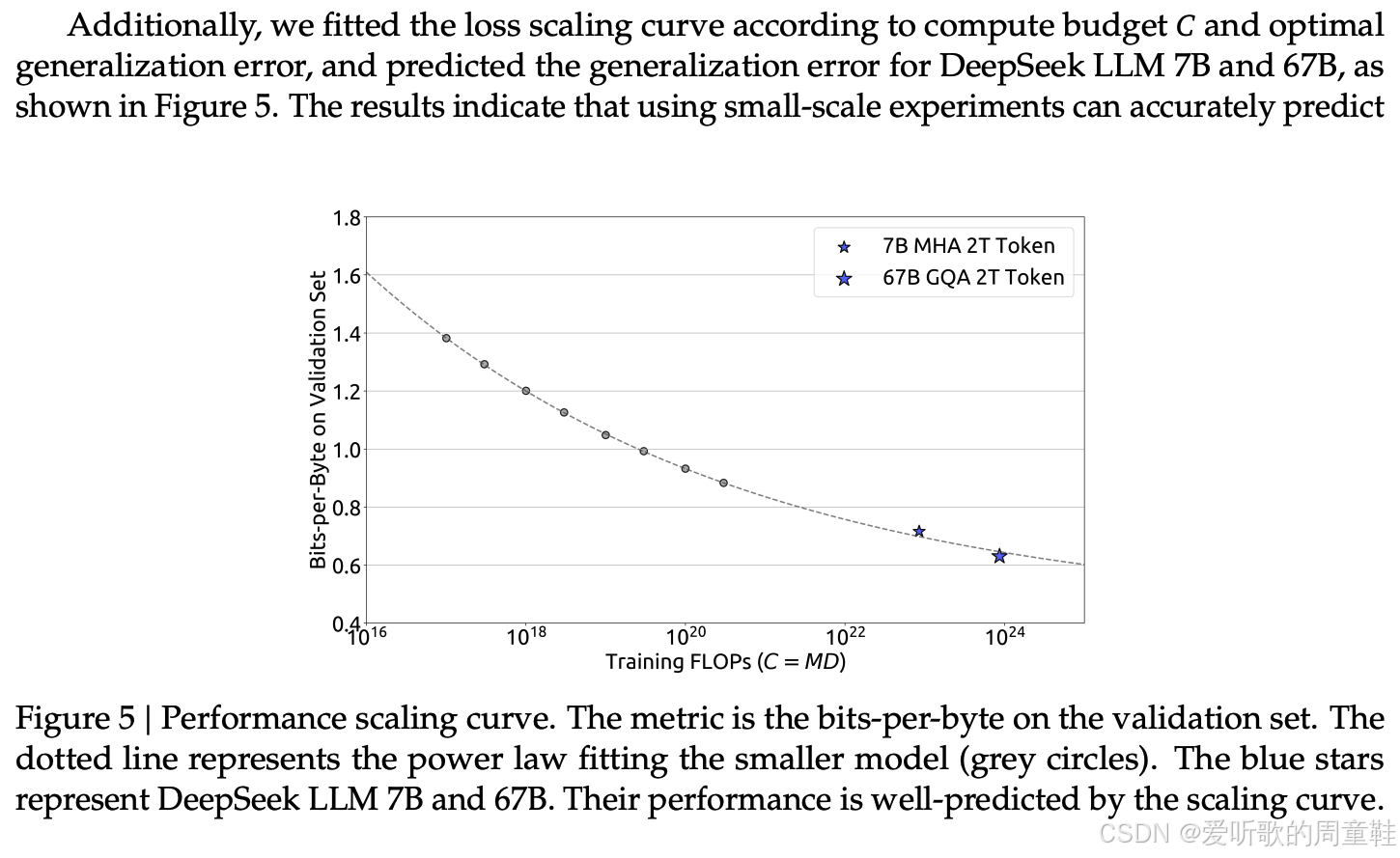
最终他们成功拟合出了缩放定律，从某些方面来说这并不意外，毕竟这是在调整完缩放策略后得到的结果，他们采用了可预测的缩放方法，他们尝试预测 7B 和 67B 模型的表现，这虽在诸多方面不足为奇，但令人惊叹的是，他们能够从约 10^20 到 10^24 的规模进行外推，并基于缩放定律精准命中预测结果，这确实令人振奋---我们能够在实际训练模型之前，就对其能力进行可量化的预测评估

以上就是 DeepSeek 的相关内容

7. Recent scaling law recipes

接下来我们将重点分析近一年来关于缩放定律的研究论文与模型进展，事实上，目前还没有任何研究能达到 MiniCPM 或 DeepSeek 的精细度水平，这些研究至今仍是 2025 年公开领域中关于模型缩放最详尽的实证研究

7.1 LLaMA 3 (2024) Scaling laws

Llama 3 的发布或许是过去一年最重要的大模型发布之一，他们的研究确实包含了一些相当有趣的模型缩放规律，首先值得思考的是：这些分析结论是否真的会在首次得出后被其他研究者复现验证

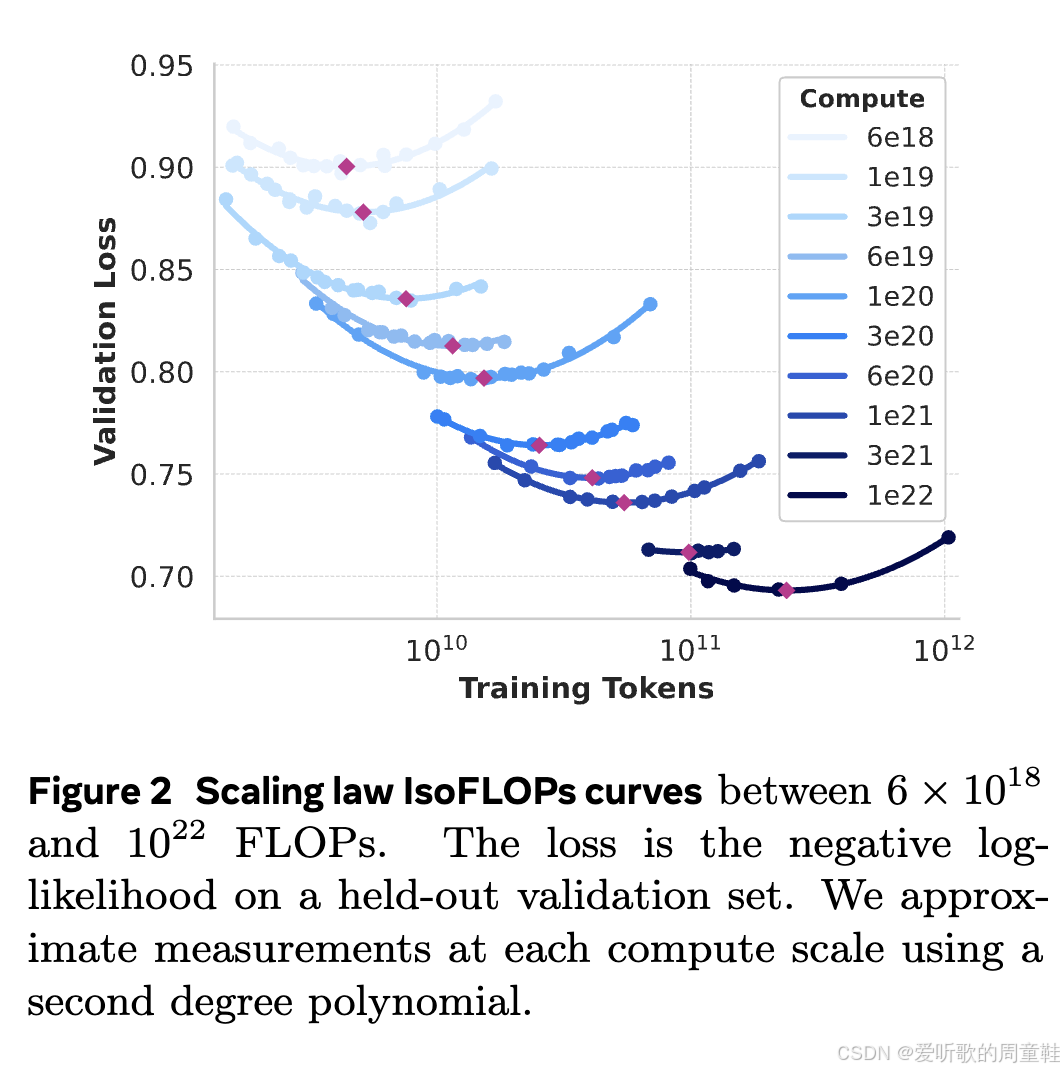
确实，Llama 3 重新验证了等计算量（IsoFLOPs）框架下的 Chinchilla 缩放定律，根据计算验证，他们最终发现的最优参数比例大约为 39.1，这个发现确实很有意思，因为 Chinchilla 原先得出的参数比例是 20:1，事实上很多人在研究过程中都曾按照 Chinchilla 比例训练过模型，很明显，20:1 这个比例实际上并不稳定，其他研究团队在反复验证过程中，普遍的得出了比原先略高的比例数值

这可能意味着架构算法效率的提升使得模型能够高效地从数据中学习，也可能暗示着其他因素，比如数据质量的提升，这些都是动态变化的影响因素，因此很难确定究竟是什么导致了这些细微的比例差异，但实验结果相当明确：拟合效果总体良好，最终确实得出了 40:1 的比例关系

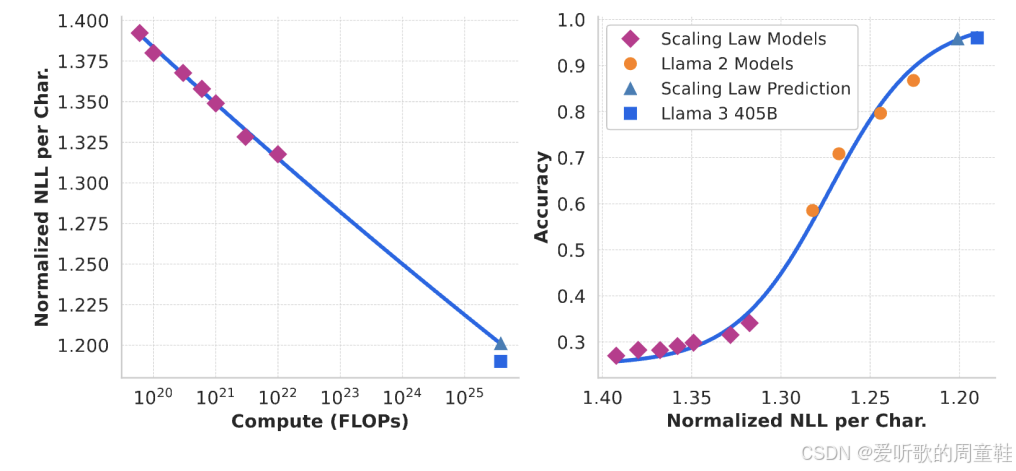
另一个与数据缩放密切相关的内容，正如我们在首次讲解缩放定律时开头部分提到的，Llama 3 团队有个很有意思的做法：他们先将模型输出转换为负对数似然（NLL）形式的损失值，再将这些 NLL 指标与下游任务准确率建立关联分析。因此他们的核心思路是希望构建的缩放关系不直接依赖于对数似然指标，这并非他们真正关注的核心指标，他们真正在意的是提升各类基准测试的表现，不论是 MMLU 还是其他被选作优化目标的评测指标

既然如此，他们就需要建立一个转换系数，将基于字符的负对数似然或类似困惑度的指标，映射到具体任务的准确率上。他们在 Llama 3 中进行了相关研究，通过拟合两组 S 型曲线建立关联：先对小模型和部分 Llama 2 模型进行拟合，再对整个数据集进行 S 型曲线拟合，结果表明，基于这些拟合结果能准确预测 Llama 3 405 B 在基准测试中的表现，这确实很有意思

据称他们将这些研究思路应用在了数据筛选环节，不过具体细节似乎披露得不多，目前尚不确定这究竟是 Llama 3 训练过程中的核心方法，还是作者团队出于兴趣开展的辅助性规模研究

7.2 Hunyuan-1 (2024) large scaling laws

近期另一项引人注目的成果是来自中国的 Hunyuan-1 大语言模型，其实现水准同样可圈可点，他们正在训练混合专家模型（MoE），由于正在训练混合专家模型，他们计划重新进行 Chinchilla 式的参数规模分析

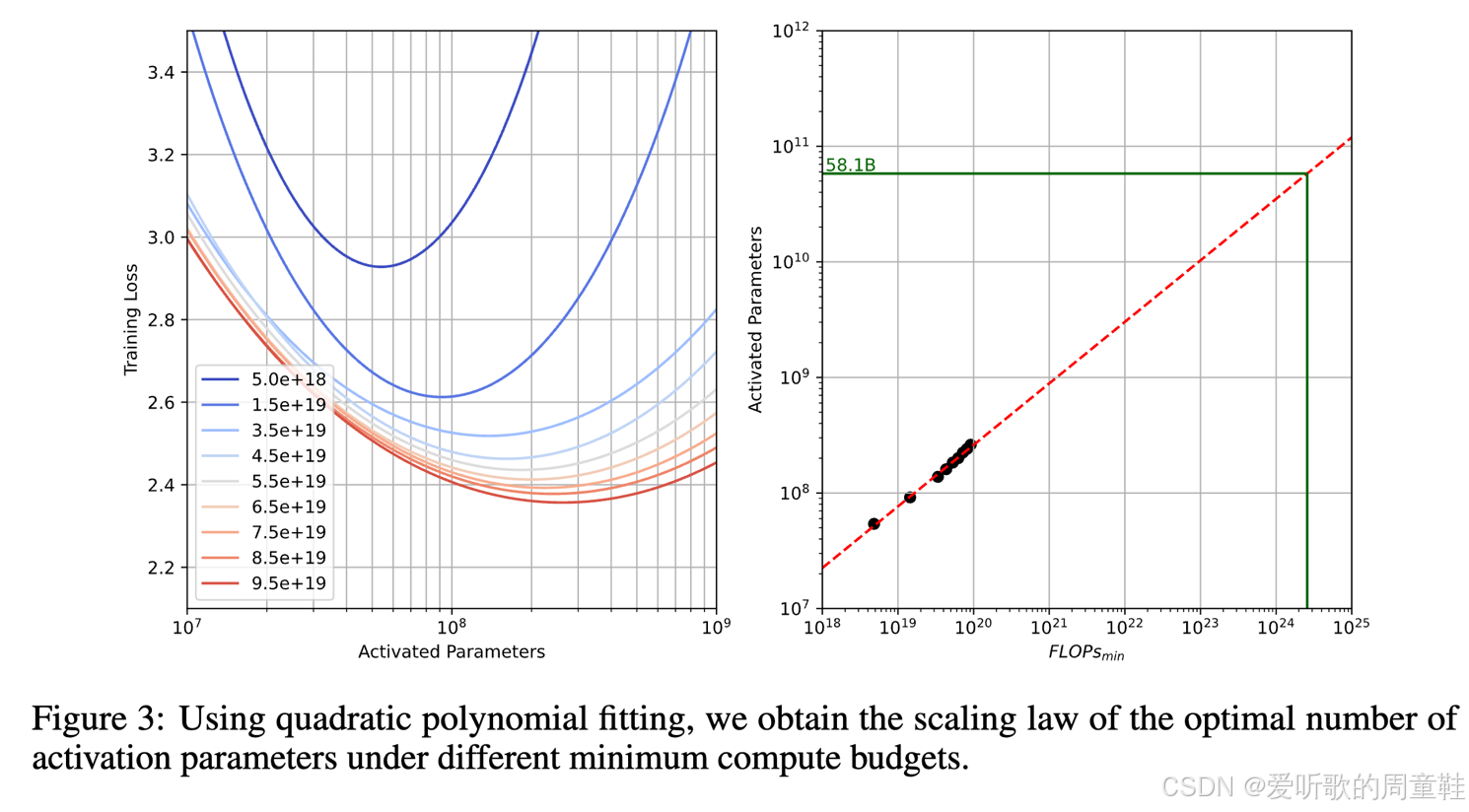
他们再次进行了等参量分析，他们采用了二次函数拟合，通过计算极值点，他们确定了新的 token 与参数配比，最终得出了 96:1 的训练数据与激活参数配比，由于 MoE 架构的特殊性，这些配比显然会存在显著差异，我们并不预期会得到与 Chinchilla 模型相同的结果

事实上，我们在多篇论文中反复观察到对 Chinchilla 模型的复现研究，因为许多研究者都迫切希望探究 token 量与参数规模的配比极限，我们更倾向于保持较高的数据参数比---让训练数据量远超参数量，这样既能确保模型的实际应用价值，又能显著降低推理成本，正因如此，业界才会不断复现 Chinchilla 的研究范式

从多个维度来看，这堪称缩放定律研究中最具可复现性的经典案例，真正难以稳定复现的，其实是 20:1 这个具体参数比例，但一个清晰且一致的规律始终成立：通过等量计算资源（isoflops）配置，总能找到参数量与数据量的最优平衡点，这种计算效率与模型参数间的可预测取舍关系具有高度稳定性，某种程度上可视为缩放定律领域一个更具突破性的新范式

7.3 MiniMax-01 (2025)

最后要提的是 MiniMax-01，这个去年才问世的研究成果，MiniMax-01 是由中国初创企业 MiniMax 推出的线性长下文语言模型，而他们的核心研究方向在于将传统二次复杂度的 softmax 注意力机制革新为线性复杂度---通过他们研发的 Lightning Attention 层实现，这种线性注意力机制能显著降低计算耗时，该团队还开发了混合架构版本模型

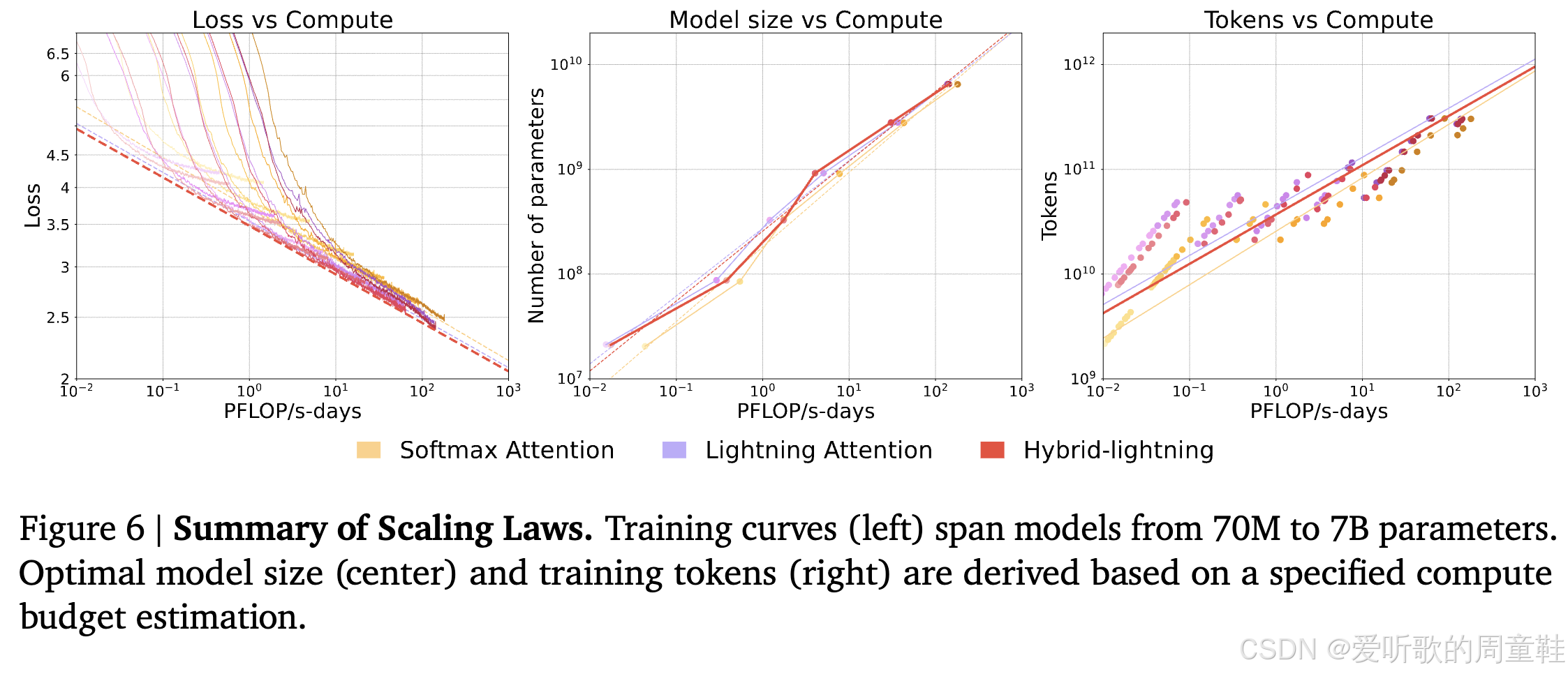
他们正致力于量化模型性能的代价曲线，从传统的 softmax 到线性注意力，再到混合架构的演进过程中，模型表现究竟会承受怎样的折损。为此，他们采用了类似 Chinchilla 研究中的方法 1：通过分析损失曲线的下包络线来评估不同注意力机制的性能边界，在训练过程中，他们会动态追踪两个核心指标：隐含最优模型规模与隐含最优训练 token 量

通过大致估算他们最终得出的结论时：Lightning 与混合架构模型的性能表现与标准 softmax 注意力机制基本持平，因此，基于这些架构训练长上下文模型是完全可行的，我们在研究论文中经常看到上面这类曲线图，如果你查阅 Mamba 论文、DeltaNet 论文或其他任何关于线性时间复杂度 RNN 的研究，都会看到类似的对比曲线图

这些论文通常会宣传：在计算资源消耗的函数关系上，完整注意力机制的扩展性与我们线性注意力机制的扩展性基本一致。但这次的情况实属罕见，我们看到的几乎是首个由主流技术团队在大规模实际部署中复现出相同结论的

7.4 Summary

综上所述，虽然我们刚才快速列举了一系列小型案例分析，但核心结论已然清晰，下面我们稍作总结

我们发现这些扩展方案中存在几个共通的关键要素，Cerebras-GPT 与 MiniCPM 均采用 μ P \mu P μP 方法确保超参数在不同规模下的稳定性，其中 MiniCPM 尤为突出地运用了其推广地 WSD 学习率调度策略，这种创新使其能够实现 Chinchilla 式地模型高效扩展，Cerebras-GPT 并未刻意复现 Chinchilla 的实验设计

DeepSeek 采取了略有差异的技术路线，他们认为大多数超参数本质上不会随模型规模而变化，但他们针对 batch size 和学习率进行了完整的扩展性分析，并运用缩放定律来推导最优的扩展方案，他们采用了等计算量分析法，他们再次复现了 Chinchilla 实验来确定模型规模参数，确保各项指标处于合理的数量级范围

在近期发布的模型中，仅 Llama 3 和 Hunyuan 采用了等计算量分析法，Llama 3 在此基础上略有扩展，但核心方法依然如此。而 MiniMax 则采用了更具创新性的方法，通过缩放定律的视角来验证其架构设计的合理性

但总体而言，我们发现业界主要复现几个关键要素：Chinchilla 参数配置仍是基准范式，而学习率和 batch size 的调优才是最受关注的核心问题。模型扩展时，这些团队通常采用固定宽高比的方式，仅通过等比放大模型总规模来实现扩展，这通常就是人们应对模型扩展过程中诸多变量调整的通用方法

8. Validating and understanding muP

本次讲座的第二部分也是最后部分，我们将重点解析 muP（ μ P \mu P μP）理论，通过前面的案例分析可以看到正确设置学习率和 batch size 确实是研究者们最核心的关注点之一，理想情况下我们应该采用具有尺度不变性的超参数，事实上，我们对参数初始化和各层学习率的选择本质上都具有任意性

参数的初始化方式本质上没有优劣之分，采用这种或那种初始化方案都不存在必然理由，因此，若能通过调整这些自由变量来实现学习率的尺度不变性和稳定性，那将带来突破性的改进，这将极大简化我们的工作流程，也能显著提升小规模实验的可行性

首先我们将从数学推导的角度展开说明具体是如何演算得出的，其理论依据是什么，实现模型可预测性扩展背后的核心概念是什么。接下来我们会分享一篇相当精彩的预印本论文 [Lucas Lingle 2024]，作者是一位独立研究员，主要针对 muP 进行了一系列消融实验研究，什么因素会导致它失效，稳健机制的作用是什么，它能在真实的 Transformer 语言模型上运行吗，这些问题在我们要讲的这篇预印本论文中已有深入探讨，我们会在最后部分详细展开

8.1 What is muP, anyway?

muP 究竟是什么，前两节课可能讲得太急了，因为虽然提到了这个概念，但还没有真正向大家解释它最核心得理论基础，不过话说回来，这么做也情有可原，毕竟大多数文献对 muP 得解释本身也都不够清晰，这些文献通常只会简单地说：把初始参数按宽度倒数（1/width）缩放，每层学习率也按宽度倒数调整就完事了，不过 muP 背后的设计理念其实很有意思，值得深入探讨，因为这些思想触及了深度学习领域反复出现的核心范式

因此，我们将以 A Large-Scale Exploration of μ \mu μ-Transfer 这本预印本论文作为讲解基础，如果你想深入了解 muP，那推荐你阅读这篇论文。这篇论文和另一篇题为 A Spectral Condition for Feature Learning 的文章是目前对这一范式最清晰易读的两份解读材料，我们将以这篇论文作为讲解基础，由于不同文献中的数学表述存在细微差别，在此特别说明：我们将严格采用 A Spectral Condition for Feature Learning 这篇论文中的数学表达形式

muP 的核心思想建议在以下几个相对简单的原理之上：在训练神经网络时，我们认为应该确保两个关键特性：当我们对神经网络进行规模扩展时，我们将保持网络深度不变，同时逐步增加网络的宽度，在逐步增加宽度的过程中，我们需要确保初始化阶段的激活值始终保持 Θ ( 1 ) \Theta(1) Θ(1) 的量级，随着网络宽度的增加，激活值的幅度应当保持相对稳定---即被通用常数上下界约束，维持大致恒定，其数值不应出现爆炸性增长，也不应衰减至消失 ，这看起来是各非常自然的要求，激活值不应过大，这是针对每个坐标分量的约束。第二个关键特性是：在完成模型初始化后，我们在执行单次梯度更新，必须确保激活值的变化量同样保持 Θ ( 1 ) \Theta(1) Θ(1) 量级

这两个条件本质上非常合理，因为一旦违反这些约束，随着模型规模扩大，要么初始激活值会爆炸或消失，要么经过单次梯度更新后激活值会出现失控膨胀或归零，这两种情况都会导致严重的模型失效问题，需要特别说明的是，这里讨论的是单个激活值（即各坐标分量）的变化情况，因此若考虑整个激活向量的范数，其量级应保持在 Θ ( n l ) \Theta (\sqrt{nl}) Θ(nl )，其中 n n n 表示网络宽度， l l l 表示层数。由于各激活分量近似相互独立，其向量范数将呈现 n \sqrt{n} n 量级特征，其中 n n n 代表网络宽度维度的元素数量

8.2 Deriving muP (condition A1)

根据这两个约束条件，可以推导出 muP 的取值，第一个约束条件要求激活值保持稳定，这直接限定了参数初始化的取值范围，下面我们将通过一个极其简明的示例来演示这个过程

现在让我们以深度线性网络 h l = W l h l − 1 h_l = W_lh_{l-1} hl=Wlhl−1 为例展开分析，这里的 h l h_l hl 表示第 l l l 层的激活值，该激活值由第 l l l 层的权重矩阵 W l W_l Wl 与前一层激活输出 h l − 1 h_{l-1} hl−1 共同决定，没有非线性变换，也没有花哨的操作，一切准备就绪

现在说初始化，我们准备采用高斯初始化 W l ∼ N ( 0 , σ l I n l × n l − 1 ) W_{l} \sim N \left( 0, {\sigma}l I{n_{l} \times n_{l-1}} \right) Wl∼N(0,σlInl×nl−1)，所以它的均值会设为 0， I I I 这个矩阵的维度将取决于我们的激活层尺寸，它呈现为矩形形式，然后我们会设置一个超参数 σ \sigma σ，这个超参数用于控制当前层权重矩阵的噪声尺度

那么现在我们可以得出什么结论呢？首先我们需要明确初始化 h l h_l hl 的规模，那么这个问题该如何分析呢？我们可以通过分析这个系统的极限行为来研究。现在假设第 l l l 层和第 l − 1 l-1 l−1 层的神经元数量 n l n_l nl 和 n l − 1 n_{l-1} nl−1 都趋向于无穷大，当神经元数量趋近于无穷大时，权重矩阵 W l W_l Wl 的分布会逐渐收敛。根据随机矩阵理论，这是一个高斯随机矩阵，若了解随机矩阵理论的基础知识，就会知道高斯矩阵的算子范数通常会收敛于噪声尺度 σ \sigma σ 乘以两个维度平方根之和即 ∥ W l ∥ ∗ → σ l ( n l − 1 + n l ) \left \| W_{l} \right \|{*} \to {\sigma}l \left( \sqrt{n{l-1}}+ \sqrt{n{l}} \right) ∥Wl∥∗→σl(nl−1 +nl )

关键在于，我们可以近似认为 ∥ h l ∥ 2 ≈ ∥ W l ∥ ∗ ∥ h l − 1 ∥ 2 \|{h}{{l}}\|{{2}}\approx\|W_{{l}}\|{{*}}\|{h}{{l}-{ 1}}\|{{2}} ∥hl∥2≈∥Wl∥∗∥hl−1∥2 这个等式成立，因此，第 l l l 层激活值的范数约等于权重矩阵 W l W_l Wl 的算子范数乘以第 l − 1 l-1 l−1 层激活 h l − 1 h{l-1} hl−1 的范数，这个近似成立的前提是 W l W_l Wl 与 h l − 1 h_{l-1} hl−1 相互独立，在初始化阶段确实满足该条件，因此，如果你愿意，完全可以将这个近似关系直接改写为等式关系

现在，我们将选择一个特定的 σ \sigma σ 取值方案：

σ = n l n l − 1 ( n l + n l − 1 ) − 1 = Θ ( 1 n l − 1 min ⁡ ( 1 , n l n l − 1 ) ) \sigma= \frac{ \sqrt{n_{l}}}{ \sqrt{n_{l-1}}} \left( \sqrt{n_{l}}+ \sqrt{n_{l-1}} \right)^{-1}= \Theta \left( \frac{1}{ \sqrt{n_{l-1}}} \min \left( 1, \sqrt{ \frac{n_{l}}{n_{l-1}}} \right) \right) σ=nl−1 nl (nl +nl−1 )−1=Θ(nl−1 1min(1,nl−1nl ))

你只需将其理解为右侧这个表达式即可，第一个等式就是精确表达式，而第二个等式更接近渐进形式的表达式，但实际上，它等于层输入连接数平方根的倒数 1 n l − 1 \frac{1}{ \sqrt{n_{l-1}}} nl−1 1 乘以模型长宽比与 1 的较小值 min ⁡ ( 1 , n l n l − 1 ) \min \left( 1, \sqrt{ \frac{n_{l}}{n_{l-1}}} \right) min(1,nl−1nl )，当输入连接数 n n n 远大于输出连接数时，该机制便会生效

假设我们选择这个 σ \sigma σ 作为初始化参数，会产生什么效果呢？将这个值代入矩阵浓度不等式公式，同时结合之前的近似关系，通过数学归纳法可以证明，每一层的激活值大小都将保持在合理范围内，让我们逐层分析这个过程，并假设直到 l − 1 l-1 l−1 层都满足该性质

归纳假设 ： ∥ h l − 1 ∥ 2 = Θ ( n l − 1 ) \left \| h_{l-1} \right \|{2}= \Theta \left( \sqrt{n{l-1}} \right) ∥hl−1∥2=Θ(nl−1 )

若该假设成立，则可直接代入上述条件： ∥ W l ∥ ∗ → σ ( n l − 1 + n l ) = n l n l − 1 \left \| W_{l} \right \|{*} \to \sigma \left( \sqrt{n{l-1}}+ \sqrt{n_{l}} \right)= \frac{ \sqrt{n_{l}}}{ \sqrt{n_{l-1}}} ∥Wl∥∗→σ(nl−1 +nl )=nl−1 nl

最终可得： ∥ h l ∥ 2 = n l + o ( n l ) \left \| h_{l} \right \|{2}= \sqrt{n{l}}+o \left( \sqrt{n_{l}} \right) ∥hl∥2=nl +o(nl )

这正是我们想要的结果，还记得之前说过需要确保激活值保持 Θ ( 1 ) \Theta (1) Θ(1) 量级吗？这意味着其范数必须控制在 n l \sqrt{n_l} nl 的量级，这正是我们在这里得到的结果（外加一些低阶项），因此在初始化时我们会选择 σ = Θ ( 1 n l − 1 min ⁡ ( 1 , n l n l − 1 ) ) \sigma= \Theta \left( \frac{1}{ \sqrt{n_{l-1}}} \min \left( 1, \sqrt{ \frac{n_{l}}{n_{l-1}}} \right) \right) σ=Θ(nl−1 1min(1,nl−1nl ))，这样能确保初始阶段的激活值不会出现爆炸性增长

8.3 Deriving muP (condition A2)

假设大家都认同上面这个初始化方法，现在我们来推导 muP 的第二部分，muP 的第一部分讨论的是初始化方法，muP 的第二部分将聚焦学习率调整策略，那么我们应该如何理解学习率的设定呢？要探讨学习率，我们需要关注第二个约束条件，第二个条件指出：在初始阶段执行单次梯度更新后，更新量必须保持稳定，不能出现数值爆炸，也不能发生梯度消失现象，所以这意味着什么呢？

当我们在第 l l l 层权重上执行更新 Δ W l \Delta W_l ΔWl 时，这个更新量从何而来？这个更新量来源于---假设我们采用随机梯度下降（SGD），那么它将由以下表达式给出：

Δ W l = − η l ∇ h l ℓ h l − 1 ⊤ \Delta W_{{l}}=-\eta_{{l}}\nabla_{{h}{{l}}}{\ell}\ {h}{{l}-{1}}^{\top} ΔWl=−ηl∇hlℓ hl−1⊤

具体表达式为：学习率乘以损失函数 ℓ \ell ℓ 的梯度，再乘以激活值的转置矩阵，当 batch size 为 1 时，该表达式将生成一个秩为 1 的矩阵，此时对 ∇ h l \nabla_{{h}{{l}}} ∇hl 的更新是一个秩为 1 的矩阵运算，由于是秩为 1 的矩阵，因此存在简洁的解析表达式 ∥ Δ W l h l − 1 ∥ 2 = ∥ Δ W l ∥ ∗ ∥ h l − 1 ∥ 2 \|\Delta W{{l}}{h}{{l-1}}\|{{2}}=\|\Delta W_{{l}}\|{{*}} \|{h}{{l-1}}\|_{{2}} ∥ΔWlhl−1∥2=∥ΔWl∥∗∥hl−1∥2，通过推导可以验证该等式成立，通过展开计算层 l l l 更新后的最终激活值，并消去等式左右两侧共有的项，即可得到如下表达式：

Δ h l = W l Δ h l − 1 + Δ W l ( h l − 1 + Δ h l − 1 ) \Delta h_{l}=W_{l} \Delta h_{l-1}+ \Delta W_{l} \left( h_{l-1}+ \Delta h_{l-1} \right) Δhl=WlΔhl−1+ΔWl(hl−1+Δhl−1)

你会得到 h l h_l hl 的更新量是多少？我们希望该对象的范数数值保持约 n l \sqrt{n_l} nl 的水平，让我们逐一分析上面这些项，看看它们的量级如何。第一项是 l Δ h l − 1 {l} \Delta h{l-1} lΔhl−1，根据归纳假设，我们可以认为这一项是可控的，因为它正是我们定义的 Δ h l \Delta h_l Δhl 再加上条件 A1 的论证支撑，条件 A1 将确保 Δ h l \Delta h_l Δhl 的量级保持在 n l \sqrt{n_l} nl 的水平，而权重矩阵 W l W_l Wl 会维持这个范数

真正的难点在于后两项，即第二项 Δ W l h l − 1 \Delta W_{l}h_{l-1} ΔWlhl−1 和第三项 Δ W l Δ h l − 1 \Delta W_{l}\Delta h_{l-1} ΔWlΔhl−1 的论证，它们的数量级其实是相同的，我们真正需要弄清楚的只有 Δ W l h l − 1 = ∥ Δ W l ∥ ∗ n l − 1 \Delta W_{l}h_{l-1}= \left. \left \| \Delta W_{l} \right \|{*} \sqrt{n{l-1}} \right. ΔWlhl−1=∥ΔWl∥∗nl−1 这个表达式，关键在于计算前一层的范数与当前层权重更新 Δ W l \Delta W_l ΔWl 的算子范数之积---因为我们无法预知权重矩阵 W W W 的更新幅度究竟会有多大，若能预知这一点，后续推导便可水到渠成

因此剩下的论证其实相当直接明了，尽管这实际上是一团复杂的纠缠，但背后的直觉却异常清晰，这个直觉告诉我们到底需要解决什么核心问题？关键在于破解 Δ W l h l − 1 = ∥ Δ W l ∥ ∗ n l − 1 \Delta W_{l}h_{l-1}= \left. \left \| \Delta W_{l} \right \|{*} \sqrt{n{l-1}} \right. ΔWlhl−1=∥ΔWl∥∗nl−1 这个表达式，第 l l l 层权重会发生多大变化，只要算出 ∣ ∣ Δ W l ∣ ∣ ∗ \left| \left| \Delta W_{l} \right| \right|_{*} ∣∣ΔWl∣∣∗ 这个变化量，就能推导出所有相关参数，进而求解出最佳学习率，这就是我们的核心策略

那么，我们该如何计算经过一次梯度步后 Δ W l \Delta W_l ΔWl 的变化量呢？这才是问题的核心所在。这里其实暗藏着一个关键假设，这个假设大致如下：如果学习过程表现良好，那么经过单次梯度步后，损失函数的变化量 Δ ℓ \Delta \ell Δℓ 必须保持 O(1) 量级

原因何在？这是因为，当网络宽度趋近于无穷大时，我们既不希望损失值的更新幅度爆炸式增长，也不希望衰减至零，本质上，我们希望无论模型规模如果扩大，损失函数的改进幅度始终保持相近的数量级，这个假设比我们之前的条件更为严格，若该假设成立，我们便可断言：损失函数的变化量实质上等于梯度与权重变化量的乘积，也就是：

Δ ℓ = Θ ⁣ ( ⟨ Δ W ℓ , ∇ W ℓ ℓ ⟩ ) = Θ ⁣ ( ∥ Δ W ℓ ∥ F ∥ ∇ W ℓ ℓ ∥ F ) = Θ ⁣ ( ∥ Δ W ℓ ∥ ∗ ∥ ∇ W ℓ ℓ ∥ ∗ ) \Delta\ell = \Theta\!\bigl(\langle \Delta W_\ell, \nabla_{W_\ell}\ell \rangle \bigr) = \Theta\!\bigl( \|\Delta W_\ell\|{F} \, \|\nabla{W_\ell}\ell\|{F} \bigr) = \Theta\!\bigl( \|\Delta W\ell\|{*} \, \|\nabla{W_\ell}\ell\|_{*} \bigr) Δℓ=Θ(⟨ΔWℓ,∇Wℓℓ⟩)=Θ(∥ΔWℓ∥F∥∇Wℓℓ∥F)=Θ(∥ΔWℓ∥∗∥∇Wℓℓ∥∗)

等式左侧为 Θ ( 1 ) \Theta (1) Θ(1) 量级，我们清楚 Δ ℓ \Delta \ell Δℓ 的变化幅度应当如何控制，准确地说，我们已知 Δ W l \Delta W_l ΔWl 的变化幅度，至此可解出梯度幅值，求得该值后，便可将其代入 Δ W l = − η l ∇ h l ℓ h l − 1 ⊤ \Delta W_{{l}}=-\eta_{{l}}\nabla_{{h}{{l}}}{\ell}\ {h}{{l}-{1}}^{\top} ΔWl=−ηl∇hlℓ hl−1⊤ 求解学习率

通过运算推导，最终可得随机梯度下降（SGD）的学习率等于：

η l = Θ ( n l n l − 1 ) \eta_{l}= \Theta \left( \frac{n_{l}}{n_{l-1}} \right) ηl=Θ(nl−1nl)

整个推导过程涉及多步运算与变量替换，其中还穿插了略显粗略的大 Θ \Theta Θ 符号近似处理，但经过这些步骤后，最终会得出一个极其简洁的公式，请注意，该结论仅适用于随机梯度下降（SGD）

此时那些始终专注盯着这个公式的读者，心里恐怕早已升起质疑，你可能会想：这存在误导性，因为在 Transformer 架构中， n l n l − 1 \frac{n_{l}}{n_{l-1}} nl−1nl 究竟代表什么？在多层感知机 MLP 中，这个比值实际上接近于 4，因为前馈层维度与模型维度之间通常存在 4 倍的缩放关系，因此这个比值基本保持恒定，在大多数模型中，这不过是个恒定常数，除非网络中的宽高比发生剧烈变化

最大更新参数化（muP）与标准参数化（SP）的核心差异在于：当前推导基于随机梯度下降场景，此时两种参数化在形式上高度相似，若针对 Adam 优化器进行完全相同的推导会发现结果存在略微差异，此时得到的将是 ∥ Δ W l ∥ ∗ n l − 1 = Θ ( 1 ) \|\Delta W_{{l}}\|{*} \sqrt{n{{l}-{1}}}=\Theta({1}) ∥ΔWl∥∗nl−1 =Θ(1)

8.4 muP mini recap...

OK，希望这个推导过程对你有所启发，我们刚才共同推导了定义 muP（最大更新参数化）的核心条件，也就是学界所称的 "谱条件"。因此，当我们想要实现类似 muP 的方法时，若直接遵循前述准则，最终将得到如下蓝色方框所示的初始化方案：

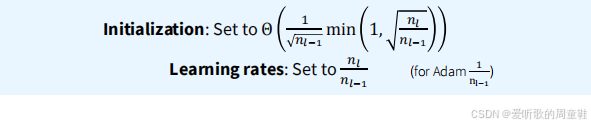
将参数初始化为 Θ ( 1 n l − 1 min ⁡ ( 1 , n l n l − 1 ) ) \Theta \left( \frac{1}{ \sqrt{n_{l-1}}} \min \left( 1, \sqrt{ \frac{n_{l}}{n_{l-1}}} \right) \right) Θ(nl−1 1min(1,nl−1nl ))，当输入维度小于输出维度时修正系数 min ⁡ ( 1 , n l n l − 1 ) \min \left( 1, \sqrt{ \frac{n_{l}}{n_{l-1}}} \right) min(1,nl−1nl ) 等于 1，否则取 n l n l − 1 \sqrt{ \frac{n_{l}}{n_{l-1}}} nl−1nl ，这就是高斯分布尺度参数的一个简易初始化方案。在使用随机梯度下降时，学习率应设置为 n l n l − 1 \frac{n_l}{n_{l-1}} nl−1nl，但若采用 Adam 优化器，设置方式会略有不同，此时学习率应取 1 n l − 1 \frac{1}{n_{l-1}} nl−11

如果你已经熟知标准初始化方法（比如 Kaiming 初始化等），不妨在脑海中将其与校准参数化方案做个对比：

在标准参数化方案中，若操作得当，高斯初始化的标准差通常应设为输入维度平方根的倒数即 1 n l − 1 \frac{1}{\sqrt{n_{l-1}}} nl−1 1，这样的设置已经非常理想，但你的学习率很可能被全局设置为固定值，这种情况对 SGD 尚可接受，但对 Adam 优化器则不尽理想，此时标准参数化（SP）与最大更新参数化（muP）的差异会真正显现出来

8.5 Implementation in Cerebras GPT

这正好把我们带回 Cerebras-GPT 论文的核心议题，至此，我们已经掌握了理解论文中所有操作所需的完整背景知识

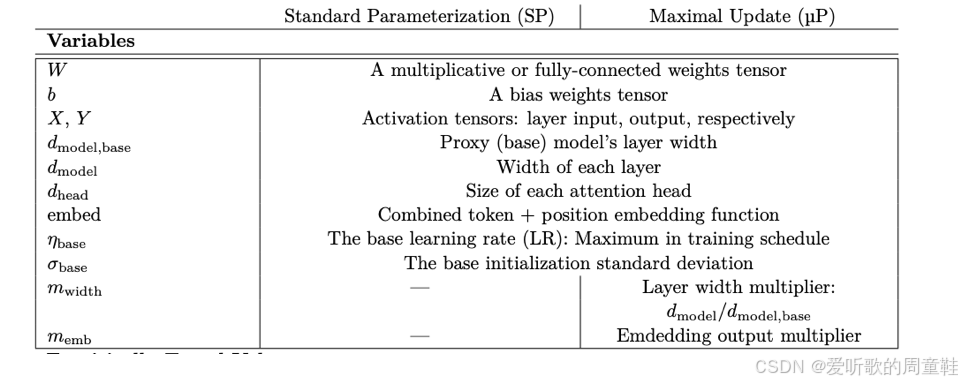
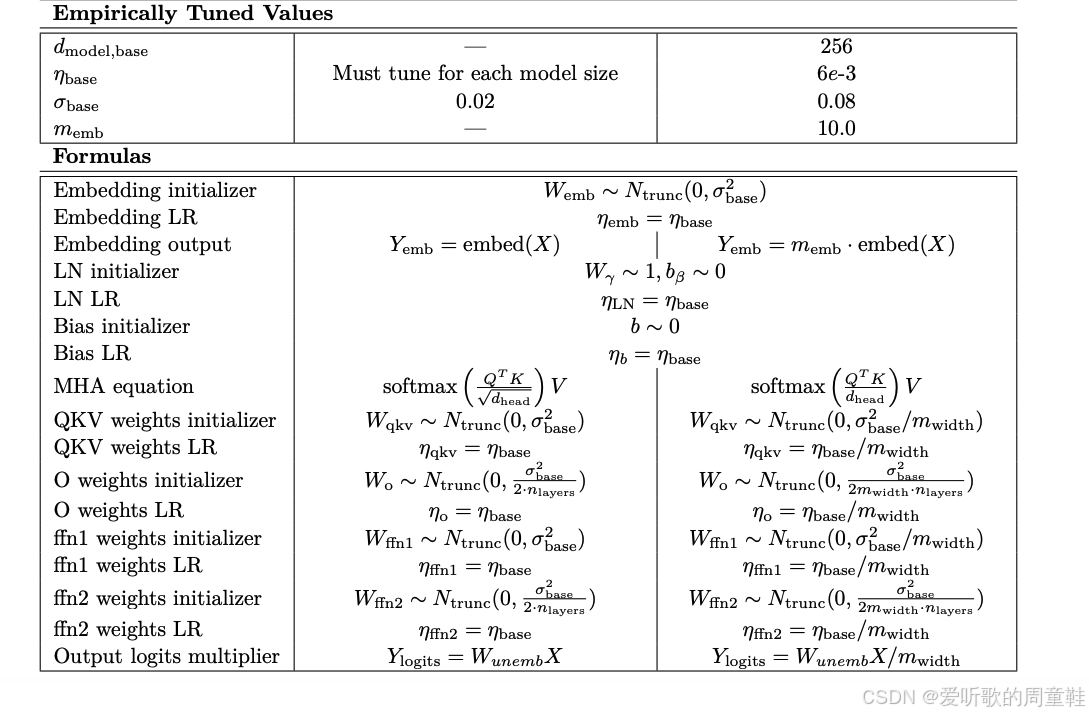
请注意，在 muP 参数化这一栏中，嵌入层需要特殊处理，由于嵌入向量采用独热编码（one-hot），其范数不会随词汇表规模线性增长，因此实际上无需进行缩放处理。不过撇开嵌入层不谈，基本上可看到所有层都会按宽度倒数（1/width）进行缩放，这就是初始化规则的核心，而学习率调整规则同样遵循宽度倒数的缩放原则，这再次印证了 Adam 优化器的学习率调整准则，若采用 Adam 优化器，这正是最恰当的处理方式，Cerebras-GPT 模型也正是采用了这一处理方式

希望以上解释足够清晰明了，这种做法的精妙之处应当已跃然纸上，通过分层调整学习率来实现更可控的模型扩展，同时，我们也能体会到将激活值和参数更新与模型宽度建立函数关联的这一设计理念的深远意义

8.6 Deeper dive into muP

以上就是 muP（最大更新参数化）在概念层面和数学原理上的核心要点，现在我们要讨论 muP 的实证研究维度，接下来我们将通过一篇论文 A Large-Scale Exploration of μ \mu μ-Transfer 来展开讨论，该研究对 μ \mu μ 参数迁移进行了大规模系统性探索，这篇研究特别有价值的地方在于它包含了一系列消融实验

具体操作上，研究者采用我们讨论过的 muP 方法，他们对权重方法进行缩放调整，将学习率按照模型的全局宽度 M M M 进行比例缩放，他们主要采用固定深度的缩放方式，这种设定有些特殊，因为通常我们会同时调整深度和宽度这两个维度，但他们真正想要做的是对照实验，仅观察宽度变化的影响，并验证 muP 方法在这种特定情况下能否完美实现缩放

所有 muP 论文都存在一个微妙但古怪的共同点，如果你还记得 Transformer 架构，就会想起其中注意力机制中的激活值也需要进行特定缩放，在计算内积后，需要将结果乘以 1 / D 1/\sqrt{D} 1/D 进行缩放，这个神奇的常数正是最合适的缩放因子，muP 与其他相关论文研究采用 1 / D 1/D 1/D 替代了传统的 1 / D 1/\sqrt{D} 1/D ，出于激活值与更新量稳定性的多层考量，这一点值得特别指出，因为乍看之下，你可能不会意识到这与 muP 存在关联

架构设计大体遵循标准 Transformer 的范式，正如我们之前提到的，这些研究仅考虑了宽度维度的缩放，他们采用了一个标准的自回归预训练文本 Transformer 模型，他们的核心目标是将模型不断向更宽的方向扩展，针对 MLP 层和模型整体，他们会将残差流维度不断放大，他们的目标是当模型宽度不断扩展时，最优学习率能保持稳定不变

若这一目标得以实现，便是 muP 理论的重大胜利，这样整个研究思路应该就很清晰了，核心目标就是扩展模型宽度，我们希望最优学习率能始终保持不变

那么第一个问题就是：这套方法真的有效吗？

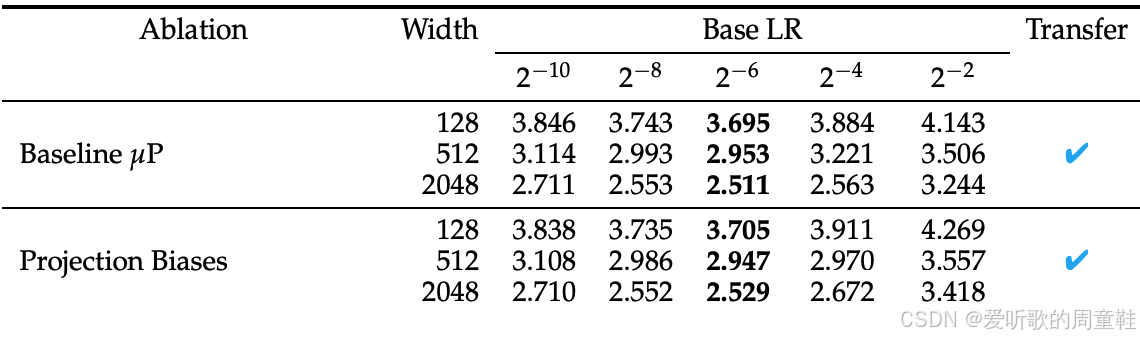
答案是肯定的，研究者设置了不同的网络宽度：128、512、2048，各列采用不同的学习率，这样的理想策略是：我们先在小规模模型上进行学习率扫描，选择最小规模的模型进行测试，然后逐步放大规模，希望这个基准学习率能始终保持最优，事实上，只要我们进行这种相对准确的宽度缩放，学习率在不同模型规模间的迁移表现得非常可靠

8.7 What is muP robust to?

于是你就会开始思考，muP 的极限在哪里？这个问题既可以从理论层面探讨，也可以在实践操作中验证，研究者准备把所有现代架构变体都试一遍，也就是人们常用的那些改进方案，包括：

Activations -- SwiGLU and squared relu
Batch sizes -- Large / small
Initialization variations -- zero attention, etc.
RMS norm gains
Exotic optimizers (Lion)
Regularizers

接着要验证：在这些架构变体中，超参数迁移的特性是否依然成立，A Large-Scale Exploration of μ \mu μ-Transfer 这篇论文很棒，因为它系统性地验证了大量不同的场景，他们尝试了不同的激活函数，他们调整了 batch size、初始化方法以及 RMSNorm 增益系数，他们甚至采用了非常规的优化器，比如正弦梯度这类特殊方法，此外，他们还尝试了不同的正则化方法，那具体哪一个因素会阻碍学习率的迁移呢？

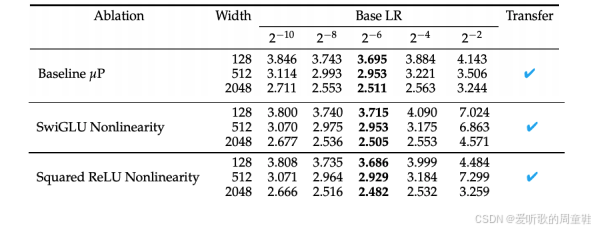
当我们调整非线性函数时，muP 理论依然适用，无论是 SwiGLU、Squared ReLU 还是作为基准的 ReLU，muP 方法他们的学习率都保持一致，完全没有变化，我们发现 SwiGLU 和 Squared ReLU 的表现就明显优于基准，这与我们在课程中学到的内容完全吻合，并不令人意外

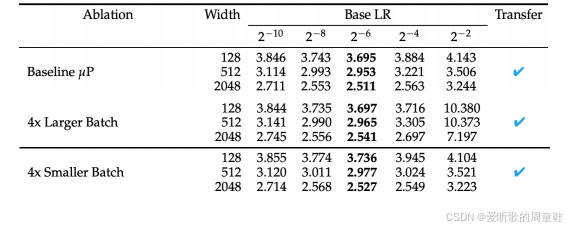
我们可能需要调整 batch size 的设置，考虑到 batch size 对模型尺度非常敏感，许多研究包括我们观察到的 DeepSeek 实验都通过拟合缩放损失与 batch size 的关系试图确定最优 batch size。我们再次观察到：当 batch size 以 4 倍为单位递减时，最优学习率始终保持稳定

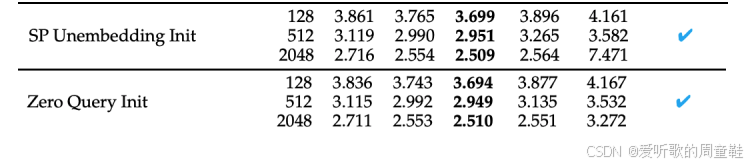
初始化方法呢？研究人员会调整某些初始化参数，例如，部分研究者会将查询矩阵初始化为 0，使所有输入项获得均匀的注意力分布。部分研究者会对顶层的嵌入层采用差异化缩放策略，具体根据标准参数化或 muP 方法而定，这种处理方式可能更具稳定性，最优学习率在这些情况下始终保持最佳效果

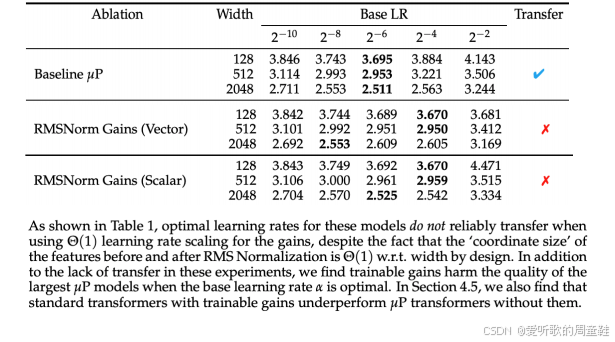
它对什么情况不够稳健呢，显然，这种方法并非适用于所有情况，例如，若引入可学习的增益参数（RMSnorm gain），这会导致 muP 失效，因此必须移除偏置项，移除偏置项后，muP 机制就能正常工作，一旦重新引入偏置项，muP 很可能再次失效

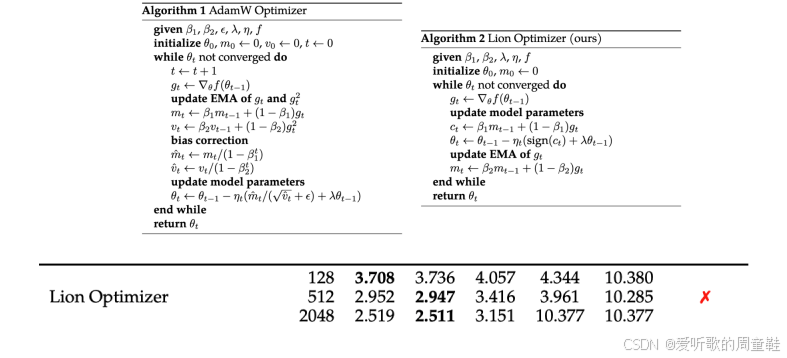
同样地，你也可以更前沿的优化器 Lion optimizer，Lion 优化器的设计确实有些反直觉，它通过对梯度取正弦函数来计算参数更新，这种操作初看颇为激进，但这种设计很可能源自进化算法等自动搜索技术，通过大规模参数空间探索最终筛选出的收敛速度最快的优化器架构

若采用这类非常规优化器，muP 的稳定性会彻底崩溃，这完全符合理论预期，muP 的架构设计专门适配 AdamW 这类特定优化器，通过精确调控参数更新幅度来维持训练稳定性，因此当切换为完全不同的优化器时，学习率参数的迁移性自然会失效，这本质上是优化动力学机制的根本性改变，这种失效确实在预料之中

最后需要指出的是，muP 对权重衰减强度异常敏感，实验表明，当权重衰减系数显著增大时，该方法的稳定性就会崩溃，这属于 muP 框架中为数不多但确实存在的显著失效案例，其余多数情况要么符合理论预期，要么本就属于非标准操作范畴，权重衰减确实是实际训练中常见的正则化手段

OK，由此可见，muP 总体上仍具有实用价值，若回归标准参数化的基准方法，很自然会思考：直接采用传统基准方法会如何呢？

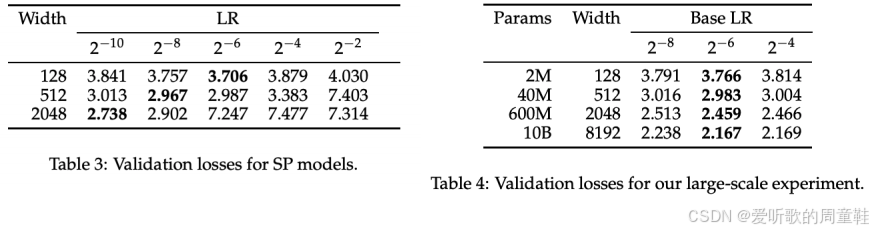
学习率必须差异化设置，采用相同学习率会导致 2048 维度的损失值显著恶化，模型会直接崩溃，产生完全失真的损失值，若坚持使用相同学习率进行扩展，结果将令人极度失望，我们还发现，学习率需要根据网络宽度的增加而按比例降低，这种变化规律是可预测的

另一方面，即便将模型规模扩展到百亿参数级别，基准损失值仍能保持稳定，他们通过大规模实验发现，学习率在 2^-6 水平时仍能保持理想状态，这个验证结果相当漂亮。因此他们在中小规模范围内完成了整个研究，他们进行了一次关键性的大规模实验，结果表明学习率仍能保持最优状态，从实验结果来看，这一发现颇具前景

8.8 Recap: scaling in the wild

综合来看，实际应用中如何进行规模性扩展呢？我们从未在超级 Chinchilla 规模上训练过 700 亿参数的模型，因此我们将高度依赖实际案例研究，我们已观察到多个实际场景中的规模化案例，我们看到研究人员运用缩放定律来设置模型超参数，特别是学习率和 batch size，我们注意到研究者采用 muP 或稳定性假设等方法，试图规避在这些参数空间中的搜索过程，此外，采用 WSD 等替代性学习率调度方案能够显著降低满足这些缩放定律所需的计算资源消耗

OK，以上就是本次讲座的全部内容了

结语

本讲我们主要讲解了大模型如何正确扩展，重点通过 Cerebras-GPT、MiniCPM 与 DeepSeek 三个代表性案例，展示现代 LLM 是如何在实践中应用缩放定律的。扩展模型的核心不是盲目堆算力，而是让 超参数随模型规模保持稳定可迁移。因此最大更新参数化（muP）成为关键，它通过在初始化与各层学习率中引入宽度缩放，使不同规模模型的最优学习率保持一致，从而让小模型上的调参结果可以可靠迁移到大模型上。

Cerebras-GPT 与 MiniCPM 都依赖 muP 稳定扩展，并结合 WSD（预热--稳定--衰减）学习率调度 来在一次训练中近似复现 Chinchilla 曲线，使 "模型规模 vs 数据规模" 的最优点能够高效确定。DeepSeek 则走另一条路线，通过系统扫描 batch size 与学习率，利用 IsoFLOPs（等计算量）曲线 精确拟合最优的计算分配策略，并从小模型外推到 7B / 67B 模型实现准确命中。

接着我们回顾了近一年缩放研究：Llama 3、Hunyuan-1 与 MiniMax-01 均复现或扩展了 Chinchilla 式的数据--参数配比规律，验证了缩放定律在不同架构（包括 MoE、线性注意力）中的适用性。

最后我们通过理论推导与实证对比验证了 muP 的核心作用：通过对初始化与学习率按宽度缩放，muP 能在模型加宽时保持激活与梯度尺度稳定，使最优学习率在小模型与大模型之间保持一致；同时也指出 muP 的局限，包括对优化器（如 Lion）与权重衰减设置的敏感性，但整体上 muP 仍是当前实现"跨模型规模可迁移调参"的最稳健参数化方式。

斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Lecture 11: Scaling laws 2

目录

前言