四、串并联谐振变换器(LCC)
1、LCC谐振变换器简介
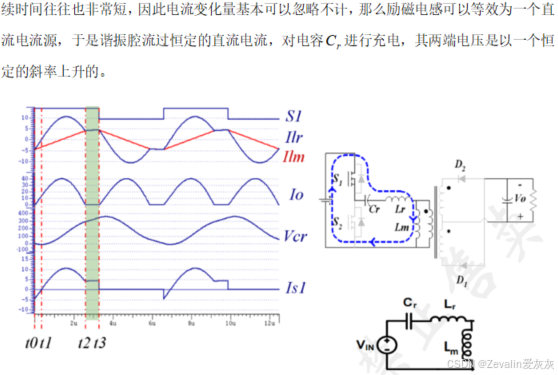
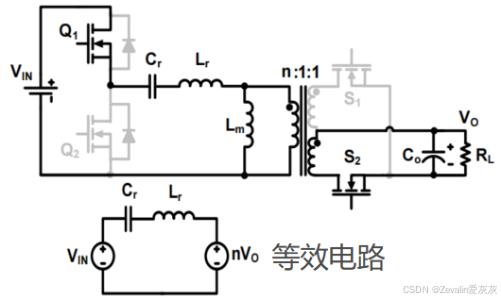
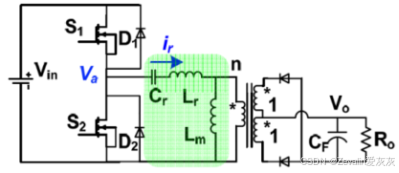
(1)下图所示的是串并联谐振变换器的电路图及等效电路图,其中在大电感条件下,负载侧可等效为一个直流电流源。
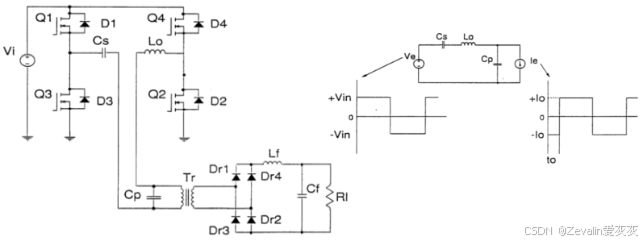
(2)有源器件的控制方案不同,那么谐振变换器的基本模态也会有所差异,下图所示的是开关频率小于谐振频率的电路响应及基本模态,分析方法和分析串联谐振变换器类似,由于使用并不广泛,这里不过多赘述。
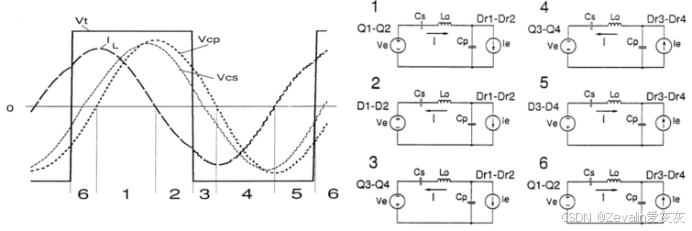
(3)串并联谐振变换器同样可能会工作在断续模式,这里不进行一一介绍。
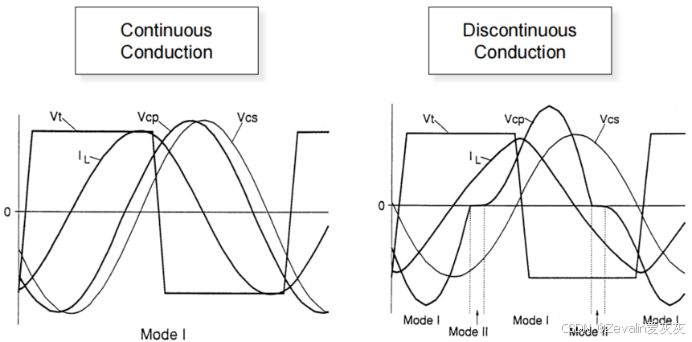
2、增益
(1)下图所示的是串并联谐振变换器的增益曲线,与前两种谐振变换器不同的是,它存在一个与负载无关的恒压输出点(即负载电阻的变化不影响电压增益,此时和
存在串联谐振),推导过程此处不过多赘述。
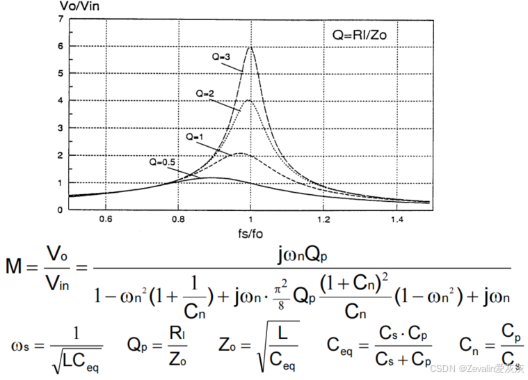
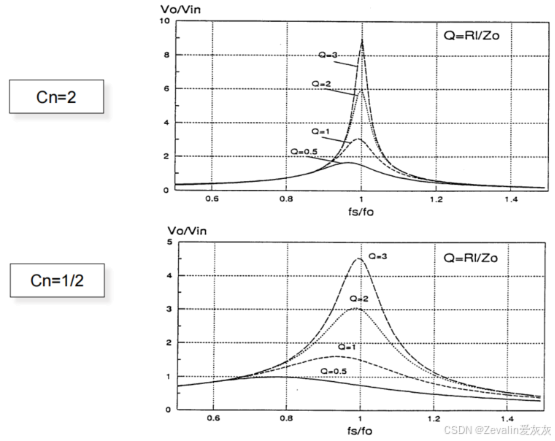
(2)从等效电路也不难看出,值的大小决定了串联谐振频率
与并联谐振频率
的相对偏移量,当
越大时,增益曲线在峰值附近的变化率越大。
五、LLC谐振变换器
1、兴起背景
(1)在设计DC/DC变换器时,需要考虑其电压工作范围,如果对输出电压的范围要求较高,也即要求浮动范围小,那么DC/DC变换器就需要应用大容量电容器以并稳定输出电压。
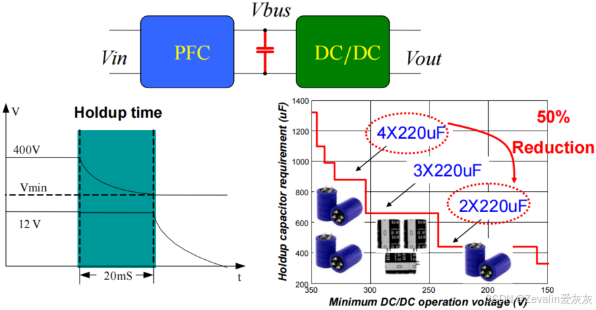
(2)设计PWM变换器时也有类似的问题,如果预期输出电压的范围较大,也即宽占空比范围要求,那么变换器的效率也会相应地较低。
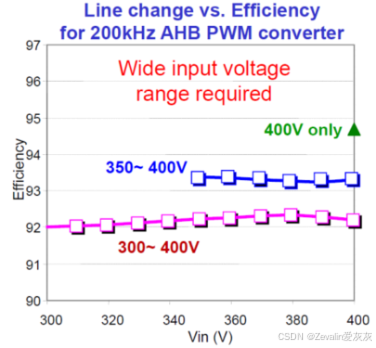
(3)前面介绍了串联谐振变换器的设计方法,其中以100%~10%负载(负载阻值的上下限倍数关系约为10倍)为例进行说明,但分析串联谐振变换器的增益曲线规律,不难看出,当负载范围变为100%~0.01%时,Q值的选取会相应地变小,这非常不利于轻载调节,并且也存在高输入电压下的关断电流及导通损耗的问题。
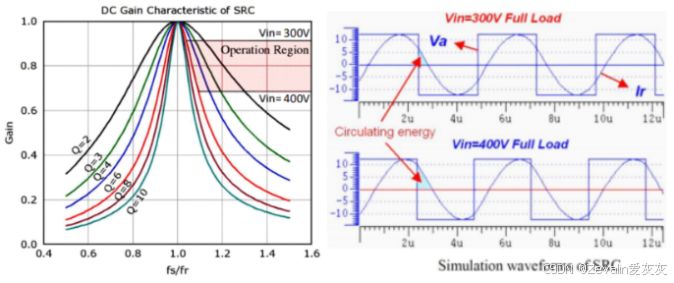
(4)并联谐振变换器不会有轻载调节的问题,但它同样存在高输入电压下的关断电流及导通损耗的问题。
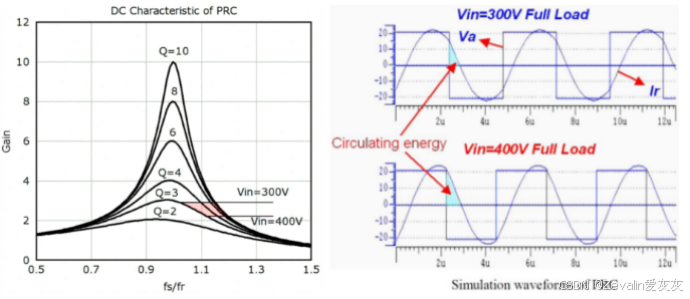
(5)LCC谐振变换器是由电路拓扑"排列组合"产生的,LLC谐振变换器也是如此,它们的增益曲线如下图所示,这种对称的结果并不意外,首先"串联路"的电容和电感能构成谐振腔,它们的谐振频率可称为"串联谐振频率",而加上"并联路"元件组成的谐振腔,其谐振频率可称为"并联谐振频率"。如果并联电容,高频电流的通过性提高,高频成分更容易产生平衡的能量置换,则并联谐振频率大于串联谐振频率,而如果并联电感,高频电流的通过性降低,不难得出并联谐振频率小于串联谐振频率,这从数学公式中也能推导出来。
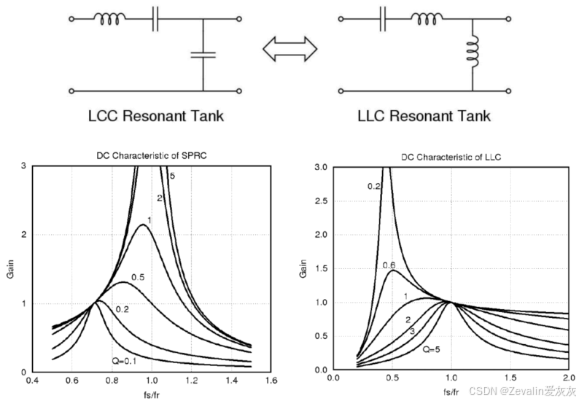
(6)LLC谐振变换器的优势:
①无论是轻负载还是重负载,输入侧开关管均能实现ZVS技术。
②负载侧二极管在特定开关频率下能够实现ZCS。
③不仅能进一步降低开关损耗,还能减小导通损耗。
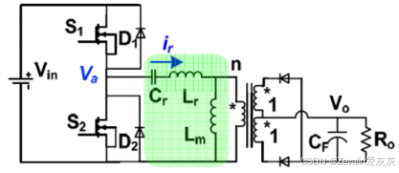
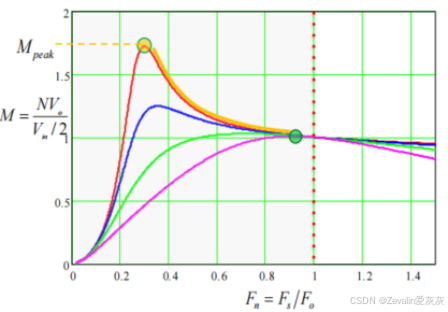
(7)下图所示的是LLC谐振变换器的增益曲线,当开关频率在串联谐振频率附近时,电路会有比较高的效率,如果输出电压降低,无论是轻负载还是重负载,都能实现ZVS技术。
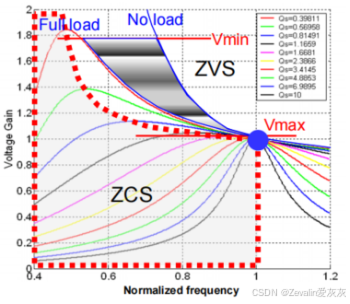
横向对比以往介绍过的变换器,在宽输出电压下,LLC谐振变换器的效率可以说是完全领先的(深紫色线为LLC谐振变换器的效率,粉紫色线为PWM变换器的效率)

2、模态分析与软开关实现
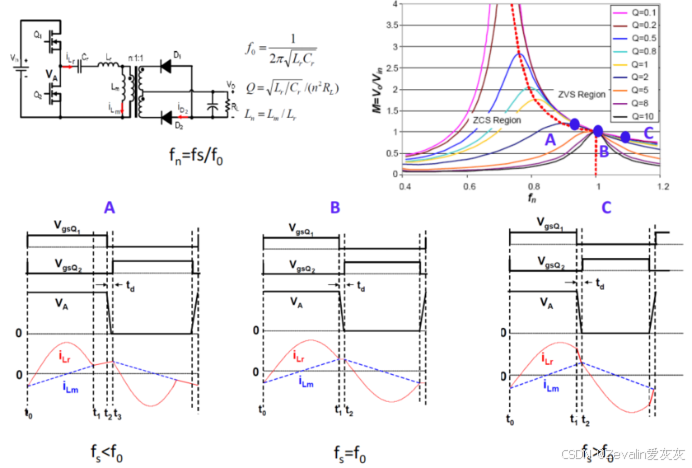
(1)LLC谐振变换器大致可分为下图所示的三个工作区间,三个区间的交界点即为串联谐振点。
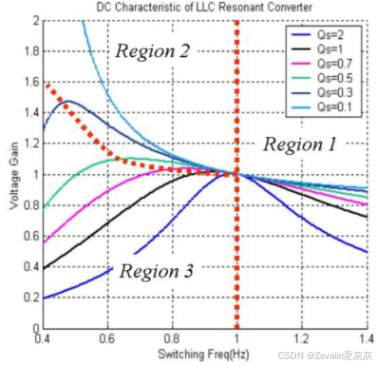
(2)当LLC谐振变换器工作在区间2时,它普遍具有6个模态,不过前三个模态与后三个模态具有高度对称性,因此仅介绍前三个模态的工作流。
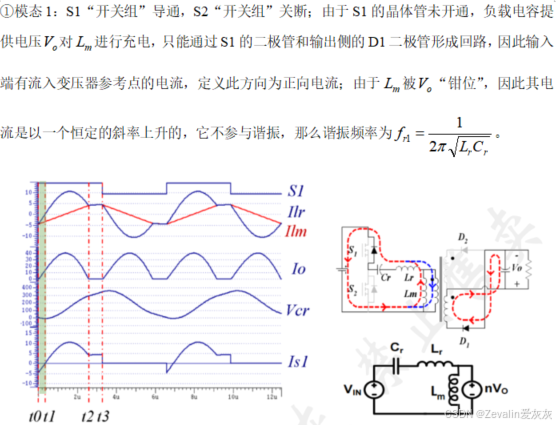
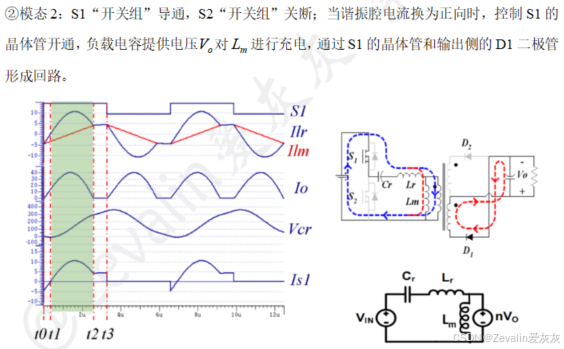

(3)ZVS技术与ZCS技术的实现:


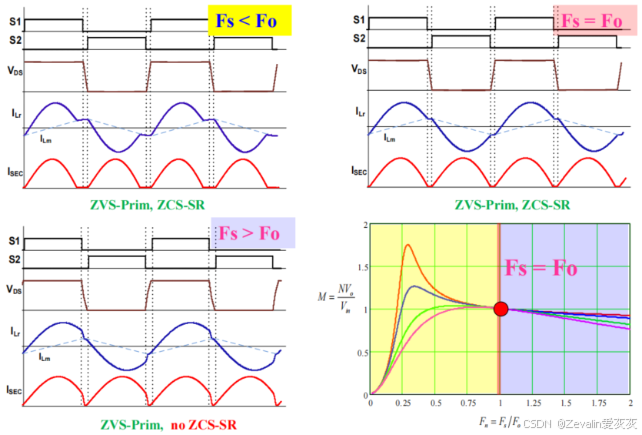
3、状态轨迹
(1)应用同步整流技术,可以将LLC谐振变换器输出侧的二极管替换为晶体管,在二极管应该导通的时候控制晶体管导通,在二极管应该截止的时候控制晶体管截止。
(2)使LLC谐振变换器工作在区间2,同样地,仅介绍前三个模态的状态轨迹。
①模态1:

②模态2:
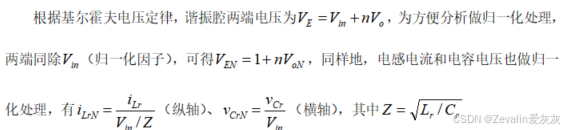
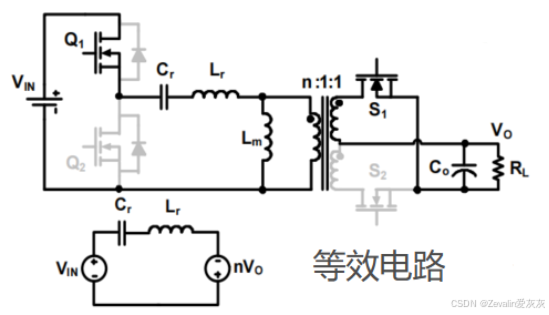
③模态3:

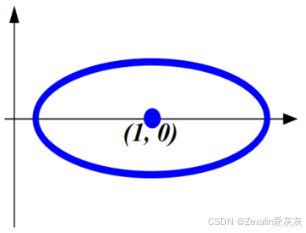
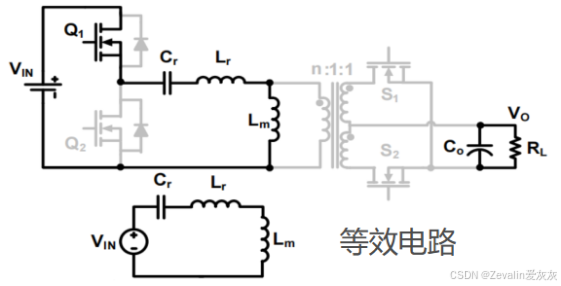
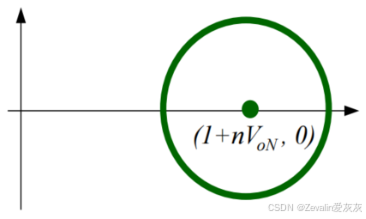
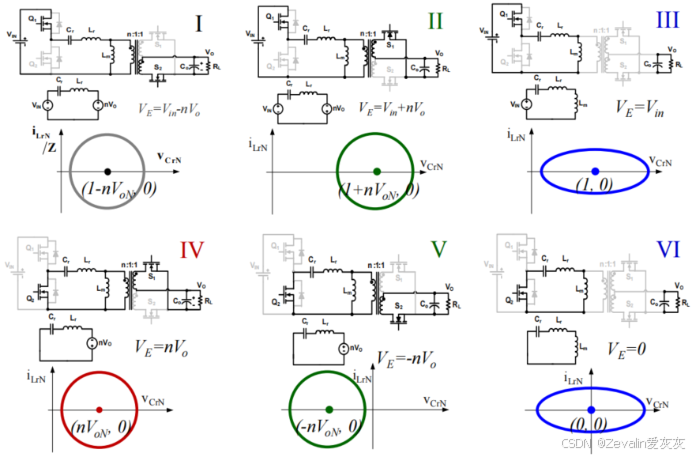
④6个模态的状态轨迹如下图所示,前三种模态的分析和后三种是高度对称的。
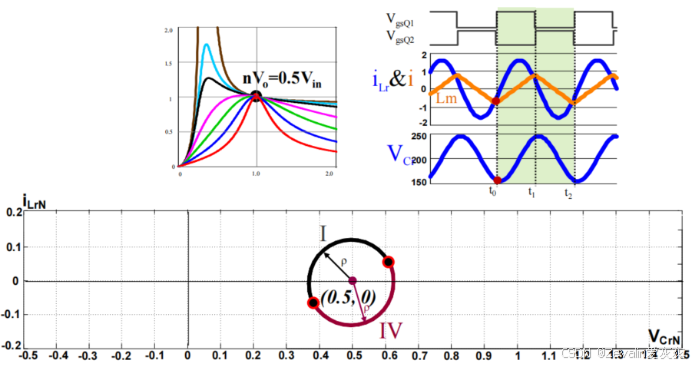
(3)不同开关频率对应的状态轨迹:
①开关频率等于串联谐振频率:
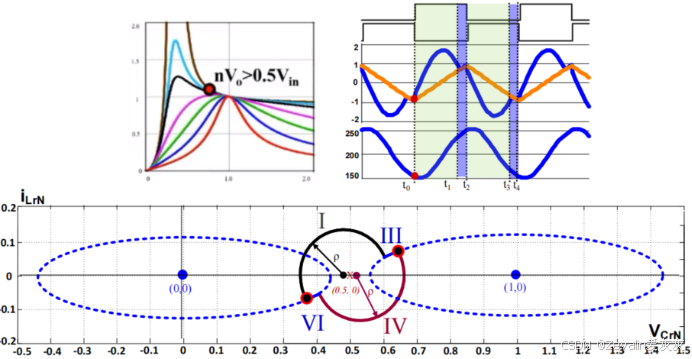
②开关频率大于串联谐振频率:
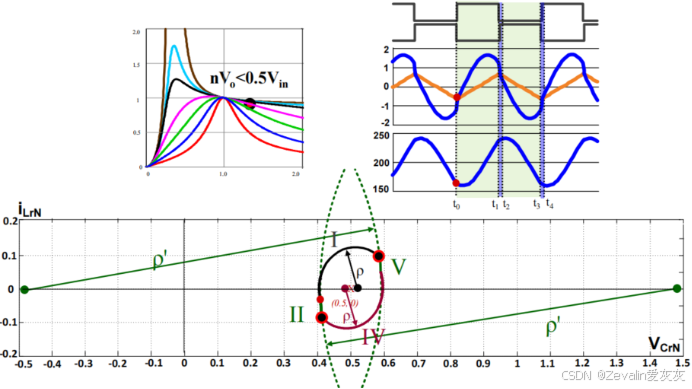
③开关频率小于串联谐振频率:
4、设计方法与数学模型
(1)在设计LLC谐振变换器时,往往不会让它工作在串联谐振频率上,原因主要有两个,一是输出电压有纹波,这将导致工作点可能在串联谐振频率附近来回抖动,二是预留一定的调节余量。
(2)在设计LLC谐振变换器前,先对LLC谐振变换器进行数学分析,为了简便计算,进行数学分析时可将开关死区忽略不计(当死区时间远小于开关周期时,可将死区移除,死区两端拼接,不影响死区中的参量求解),假设开关频率等于串联谐振频率。



(3)设计步骤举例及数学模型优化:
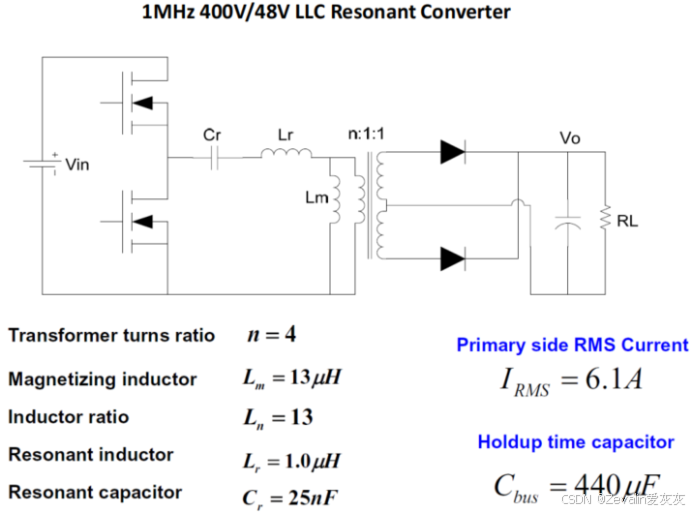
①需求为(最大)输入电压为400V,输出电压为48V,输出功率为1000W,输出电压稳压时间(Hold-up time)为20ms,电路效率大于95%,负载变化范围为20%~100%,电路拓扑如下图所示。
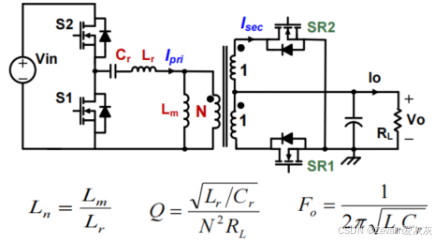
②根据经验选取开关频率,所谓"经验"比较复杂,它与器件特性等相关,此处不展开介绍。
③(最大)输入电压与输出电压之间的倍数关系通过变压器实现,倍数关系对应变压器匝数比,有。
④根据实际需求设计输入电压范围,因为实际中输入电压不一定稳定在400V,可能是一个宽范围输入电压,比如220V~400V,当输入电压低于400V时,谐振变换器相应地需要提高增益;相应地,有电压范围的选取就有工作点位置的确定,串联谐振频率点往右,该谐振变换器相当于串联谐振变换器,负端无法实现ZCS,且不利于轻载调节,同时为了源端能够实现ZVS,工作点需要选取在增益曲线的"区域二"中。
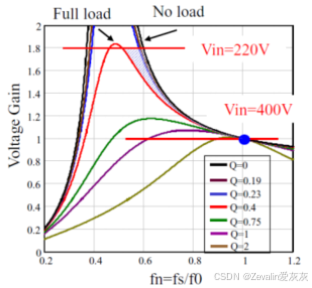
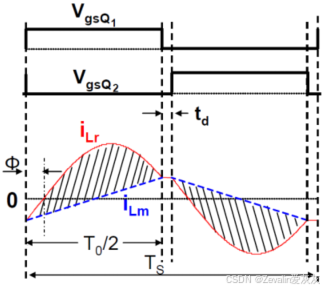
⑤在开关死区中,开通晶体管前需要对晶体管的结电容进行放电,关断晶体管前需要对晶体管的结电容进行充电,这个过程是近似恒定不变的,根据电容的伏安特性,结电容的两端电压就是近似线性变化的,结合先前对LLC谐振变换器进行的数学分析,可以得出开关死区内的电感电流为
,在此电流下,需保证死区时间
内
能够完成结电容的充/放电,根据电荷守恒,有如下表达式,其中
为单个晶体管结电容大小为降低导通损耗,需最小化有效值电流,优先选择较大的电感值。
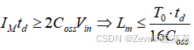
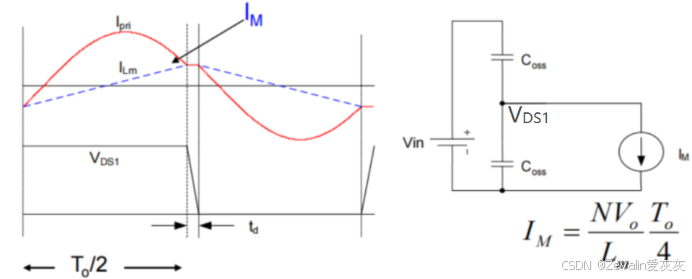
⑥上一步的结论是建立在死区时间远小于开关周期的基础上的,如果死区时间无法忽略不计,(开关周期与串联谐振频率
作差的结果越大,死区越难忽略),那么整个电路的数学模型需要进一步优化(要想进一步减小有效值电流,励磁电感的选取值需要更大,相应地,死区时间也需要加长,这种制约关系在忽略死区时是矛盾的,因此必须优化数学模型)。
在忽略死区得出的励磁电感电流表达式的基础上考虑死区(仍然将死区中的励磁电感电流近似为恒流),可得
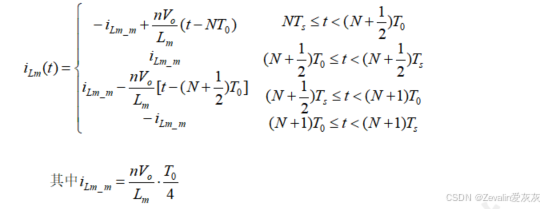


⑦最后确定及
,它们的关系为
,这意味着
越大,Q值将会越小,那么开关频率将会处在更窄的频带中,且经过数学分析也能看出,
越大,谐振腔电容所受的电压应力也会更小,晶体管的有效值电流(导通损耗)也会更小,因此往往希望
尽可能往大取值。

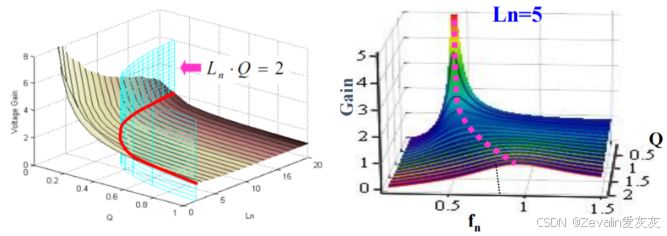
⑧不同和Q值的组合所能达到的最大电压增益不同(开关频率等于并联谐振频率时达到最大电压增益),三个变量可构成一个三维空间中的扭曲平面,同时
和Q值的数值关系也可构成一个三维空间中的扭曲平面,两平面相交,得到关于
和Q值的增益曲线,增益曲线的最小值需大于输入电压为最小值时谐振腔所需的电压增益,否则无法满足需求。
⑨开关频率选取1MHz,一种设计结果如下图所示。