一、LCL 滤波器电路模型
推导前需明确 LCL 的电路结构和变量定义,本文以并网逆变器场景为背景,考虑实际电网的感性阻抗(忽略电阻,因高频下感抗主导)。
1.1 电路模型与变量定义
LCL 滤波器核心由 "逆变器侧电感\(L_1\)、滤波电容C、网侧电感\(L_2\)" 组成,电网等效为 "理想电压源\(v_g\)串联电网电感\(L_g\)"(\(L_g\)反映电网强度,强电网\(L_g≈0\))。
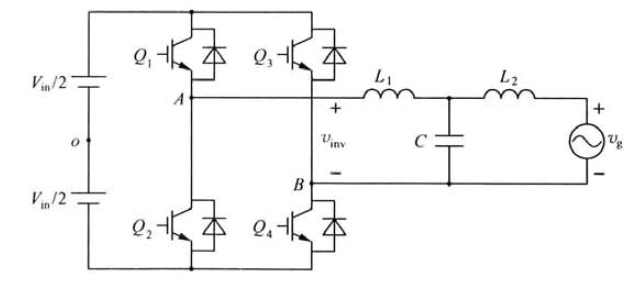
关键变量定义:
- 输入:逆变器桥臂输出电压\(v_{inv}(t)\)(控制侧输出,决定滤波前的电压特性);
- 输出:并网电流\(i_2(t)\)(流入电网的电流,核心控制目标,需满足谐波标准);
- 中间变量:\(L_1\)电流\(i_1(t)\)、滤波电容电压\(v_c(t)\);
- 电网参数:电网电压\(v_g(t)\)、电网电感\(L_g\)(弱电网\(L_g\)增大,强电网\(L_g≈0\))。
假设条件:
- 所有元件为理想器件(无寄生电阻、电容);
- 零初始条件(拉普拉斯变换时,初始电流 / 电压为 0);
- 电网电阻\(<1Ω\),高频下影响可忽略,暂不纳入模型。
二、工程常用简化场景的传递函数
实际应用中,常遇到 "理想电网""带无源阻尼" 等场景。
场景 1:理想电网(忽略电网电感\(L_g=0\))
强电网(如靠近变电站、线路短)的电网电感\(L_g≈0\),此时为最常用的基础传递函数:
\(\boxed{G_{v-i}(s) = \frac{1}{s^3 L_1 L_2 C + s (L_1 + L_2)} }\)
此式是 LCL 参数设计、谐振频率计算的核心依据,需重点记忆。
场景 2:含无源阻尼(电容串联电阻\(R_d\))
LCL 滤波器存在谐振尖峰,工程中常用 "电容串联电阻\(R_d\)" 抑制谐振(损耗小、易实现)。此时电容支路阻抗变为\(\frac{1}{sC} + R_d\),修正为:
\(v_c(t) = (L_2 + L_g) \frac{di_2(t)}{dt} + R_d \cdot C \frac{dv_c(t)}{dt} + v_g(t)\)
重新推导后,传递函数分母增加阻尼项,最终为:
\(\boxed{G_{v-i}(s) = \frac{1}{s^3 L_1 C (L_2 + L_g) + s^2 L_1 C R_d + s (L_1 + L_2 + L_g) + R_d} }\)
(阻尼电阻\(R_d\)越大,谐振抑制越强,但高频损耗也越大,通常取\(1~10Ω\),需结合开关频率优化)
三、传递函数的核心特性分析(从公式看本质)
通过LCL基础传递函数,可分析 LCL 滤波器的频率特性(令\(s=jω\),\(ω=2πf\),f为频率)。
1. 谐振频率\(f_r\)
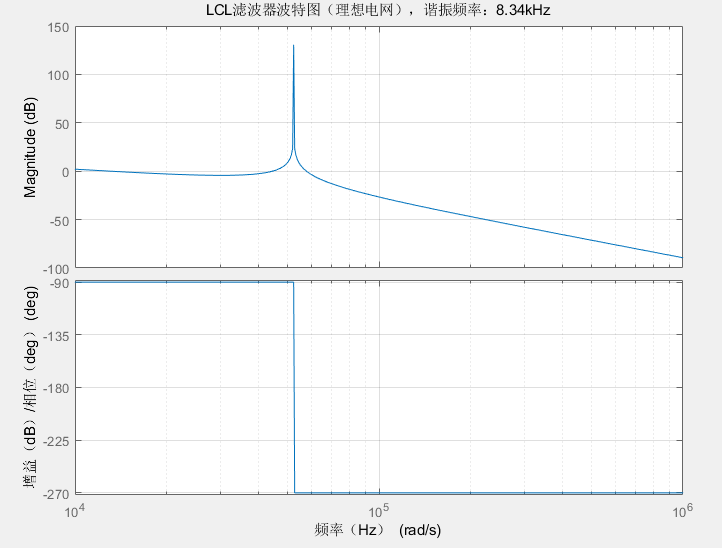
谐振频率是 LCL 的 "危险点"------ 幅频特性在此处出现尖峰,易导致系统不稳定。令分母为零(幅频特性无穷大的理论点),解得:
\(\boxed{\omega_r = \sqrt{\frac{L_1 + L_2}{L_1 L_2 C}}}\)
\(\boxed{f_r = \frac{1}{2\pi} \sqrt{\frac{L_1 + L_2}{L_1 L_2 C}}}\)
设计原则:
\\(f_r\)需避开电网谐波(如 50Hz 的 3/5/7 次)和开关频率(如 40kHz),通常取\(2f_0 < f_r < f_s/2\)(\(f_0=50Hz\),\(f_s\)为开关频率)。
2. 幅频特性斜率(滤波能力体现)
对LCL基础传递函数取幅值
\(|G_{v-i}(jω)| = \frac{1}{\sqrt{[ω^3 L_1 L_2 C]^2 + [ω (L_1 + L_2)]^2}}\),分析不同频段的斜率:
| 频段 | 频率关系 | 特性分析(近似) | 幅频斜率 | 物理意义 |
|---|---|---|---|---|
| 低频段 | \(f \ll f_r\) | 电容开路,LCL≈\(L_1+L_2\)的 L 滤波器 | -20dB/dec | 抑制低频谐波能力弱 |
| 谐振段 | \(f ≈ f_r\) | 分母两项抵消,幅值骤增 | 尖峰 | 需阻尼抑制,否则系统不稳定 |
| 高频段 | \(f \gg f_r\) | 电容短路,LCL≈\(s^3 L_1 L_2 C\) | -60dB/dec | 抑制高频谐波能力强(优于 L 滤波器) |
四、LCL滤波器波特图MATLAB绘制
Matlab
% 理想电网下LCL滤波器传递函数波特图绘制
% 传递函数:G(s) = 1 / [s^3*L1*L2*C + s*(L1+L2)]
% 参数单位:H(亨利)、F(法拉)
%% 1. 定义LCL滤波器参数(基于125kW储能变流器设计)
L1 = 62.5e-6; % 逆变器侧总电感(两模块并联,125μH×2 → 等效62.5μH)
L2 = 19e-6; % 网侧总电感(两模块并联,38μH×2 → 等效19μH)
C = 25e-6; % 滤波电容(每相25μF,三相星接)
%% 2. 构建传递函数分子和分母多项式(s域)
% 分子:num = 1
num = 1;
% 分母:den = s^3*L1*L2*C + s*(L1+L2)
den = [L1*L2*C, 0, (L1 + L2), 0]; % 多项式系数:[s³项, s²项, s项, 常数项]
% 创建传递函数模型
sys = tf(num, den);
%% 3. 计算谐振频率(理论值)
f_r = 1/(2*pi) * sqrt( (L1 + L2)/(L1*L2*C) ); % 谐振频率公式
f_r_kHz = f_r / 1000; % 转换为kHz
%% 4. 绘制波特图
figure('Name','LCL滤波器波特图(理想电网)','Position',[100,100,800,600]);
bode(sys);
grid on; % 显示网格
title(['LCL滤波器波特图(理想电网),谐振频率:', num2str(f_r_kHz, '%.2f'), 'kHz']);
xlabel('频率(Hz)');
ylabel('增益(dB)/相位(deg)');
% 在谐振频率处添加标记
hold on;
plot(f_r, -100, 'ro', 'MarkerSize', 8); % 谐振点标记(y轴取-100避免遮挡)
%text(f_r, -135, [' 谐振频率:', num2str(f_r_kHz, '%.2f'), 'kHz'], 'Color', 'r');运行上述代码后绘制出的波特图如下,可以根据自己设计的参数进行调整后绘制。