系统演示器与测量结果
对于基于OFDM的方法,已经建立了一个完整的24GHz ISM频段系统演示器,基于商业测量设备。该设置的主要组件是Rohde & Schwarz (R&S) SMJ100A矢量信号发生器、R&S SMR40微波信号发生器和R&S FSQ26信号分析仪。应用了额外的中功率放大器模块Hittite HMC498,将输出功率提高到4.2dBm的水平。信号通过提供约22dBi增益的喇叭天线辐射和接收。信号的生成和处理在MatLab中使用仿真模型的软件组件执行。设备通过MatLab仪器控制工具箱控制,允许系统的准实时操作。
为了在真实道路场景中测试OFDM概念的性能,演示器设置安装在汽车中进行测试行驶。喇叭天线安装在汽车顶部的车顶架上。其余系统组件放置在后备箱中。系统参数根据表2设置。
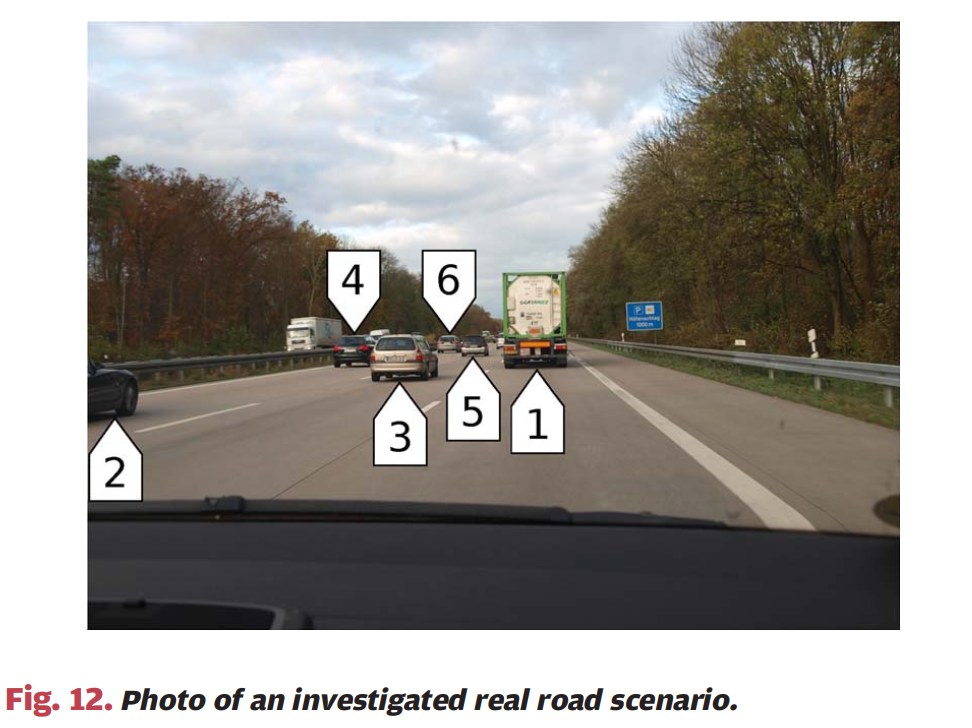
图12:图12显示了所选择的一个特定高速公路场景的照片。照片从装有RadCom系统的汽车内部向前拍摄,显示了高速公路上的多辆汽车。由于直接行驶在装有RadCom系统的汽车前面的卡车产生的强烈反射,它代表了一种最坏情况场景。所有前方行驶的汽车在照片中都被编号:卡车标记为1,右侧车道的汽车标记为3和5,左侧车道的汽车标记为2、4和6。
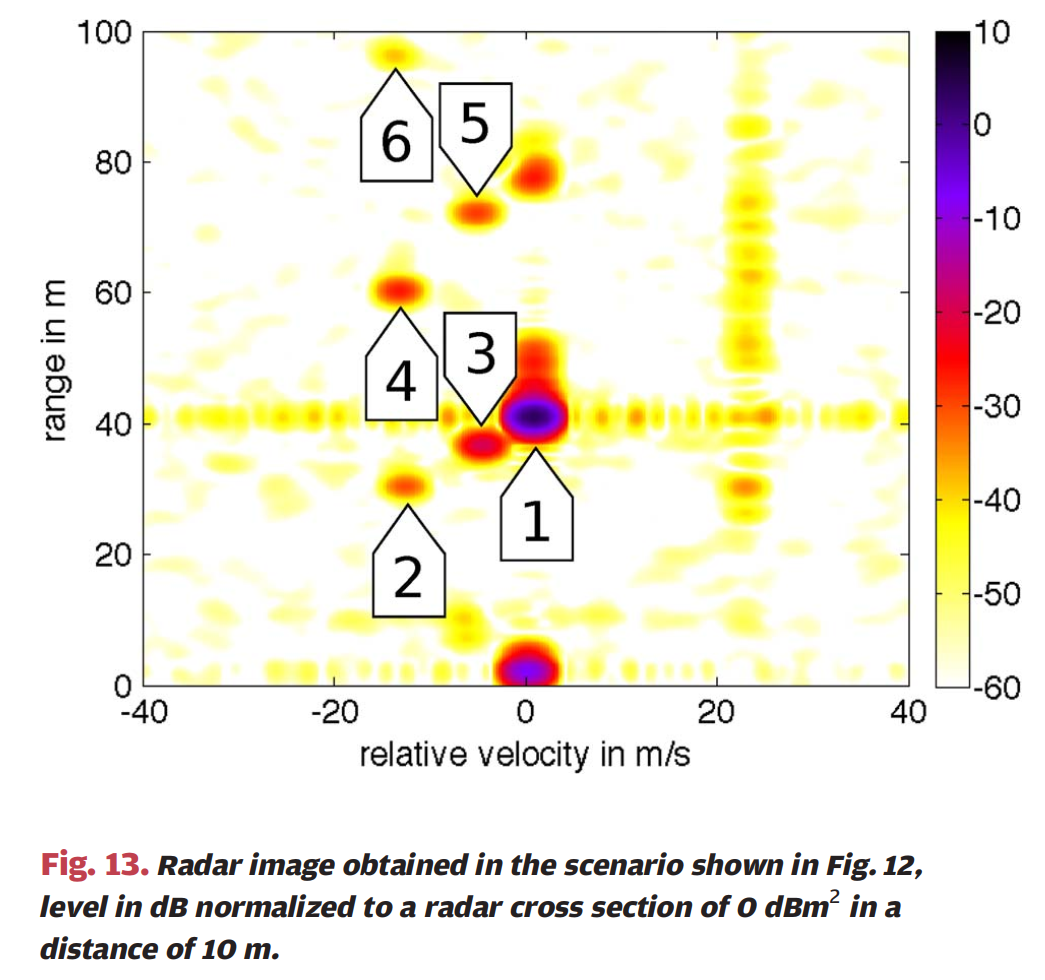
图13 :图13显示了该场景中从反射的OFDM信号获得的雷达图像,包括与相应照片中不同汽车对应的编号。横轴为相对速度(单位:m/s,从-40到40m/s),纵轴为距离(单位:米,从0到100m),颜色条表示强度(单位:dB,从-60到10dB,归一化为10m距离处σRCS=0\sigma_{RCS}=0σRCS=0dBm²的雷达截面对应0dB)。
雷达图像显示出非常高的动态范围,反射物体非常清晰。所有汽车都可以在雷达图像中识别出来。照片比雷达图像拍摄得稍早,因此在比较照片和雷达测量时,汽车2、4和6的距离由于其高相对速度而不完全一致。在近距离处,出现了相对速度为零的反射,这是由汽车底盘的反射引起的。最强的反射物体是卡车(1),其反射比第二强物体(中间车道上的汽车3)的反射高23dB。卡车的反射在雷达图像中为3.5dB,考虑到距离,这转换为σRCS=25.5\sigma_{RCS}=25.5σRCS=25.5dBm²的雷达截面。中间车道上汽车的雷达截面为σRCS=1.4\sigma_{RCS}=1.4σRCS=1.4dBm²。在雷达图像中,中间车道上行驶更快的汽车(3)和(5)显示相对速度约为-5m/s(-18km/h),左车道上的汽车(2)、(4)和(6)显示为-12m/s(-43.2km/h)。卡车引起的旁瓣沿多普勒轴显示-38.5dB的相对电平,在40m距离范围内可见为水平线,沿距离轴仅为-44.8dB,更弱。沿距离轴的降低是由于接收器中A/D转换器输入端的低通滤波器的传递函数提供了额外的窗口效应。还有趣的是,所有来自非运动物体和地面杂波的反射都可以作为相对速度为23m/s(82.8km/h)的垂直线看到,对应于装有OFDM系统平台的测试车辆的速度。背景噪声电平低,雷达图像SNR已确定为SNRimage=65.9dB(包括处理增益)。峰值背景噪声电平相对于卡车引起的峰值为-54.3dB。这证实了关于SNRimage和PSL之间比率的仿真结果(参见图11)。
因此,可以得出结论,所研究的调制符号域处理技术为24GHz ISM频段的实际应用提供了出色的性能。即使存在一个引起非常强反射的单一物体,可用的动态范围也足以检测道路上的所有汽车。独立于距离确定相对速度的能力是一个极其有用的特性,因为它创建了第二个维度,允许将所有运动物体与杂波和来自固定物体的反射区分开来。
多载波波形的结论
通过应用多载波波形和利用这些波形频率维度的专用处理技术,雷达应用的性能可以大幅提高。调制符号域处理方法允许去除信息,因此可以在传输任意用户数据的同时执行雷达测量。同时,单载波扩频方法的动态范围被超越了许多数量级,特别是对于高SNR水平,因为性能随SNR增加而增长,没有任何饱和效应。此外,还可以轻松地为每个反射物体独立于距离估计相对速度。在雷达处理中实现了高增益,即使在存在来自其他OFDM系统的干扰时也能保持。由于调制符号域处理算法中多普勒频移的固有补偿,积分时间不受多普勒限制。
该概念的可操作性和高动态范围已通过在真实道路场景中使用系统演示器的测量得到验证。对于通信应用,不需要特殊编码。因此,对于单用户,整个带宽可用于数据传输,这允许非常高的数据速率。然而,对于通信应用的多用户操作,需要额外的多址技术,例如时分多址(TDMA)。
多天线处理
波形设计的目标不仅是为雷达和通信应用开发一种通用波形,还要包括在接收器处实现多天线处理技术以进行角度反射体定位的可能性。数字波束形成(DBF)雷达系统和多输入多输出(MIMO)通信系统的接收器结构为每个接收天线提供一个单独的接收器,每个接收器由基带转换和后续的模数转换组成。理论上,多天线处理技术可以直接应用于数字化基带信号,然而,这种方法将需要极高的计算量。对于实际实现,更方便的是首先执行各个应用处理,例如在雷达应用的情况下,进行距离(和多普勒)压缩。然后,多天线技术将直接应用于这些预处理器的输出信号。
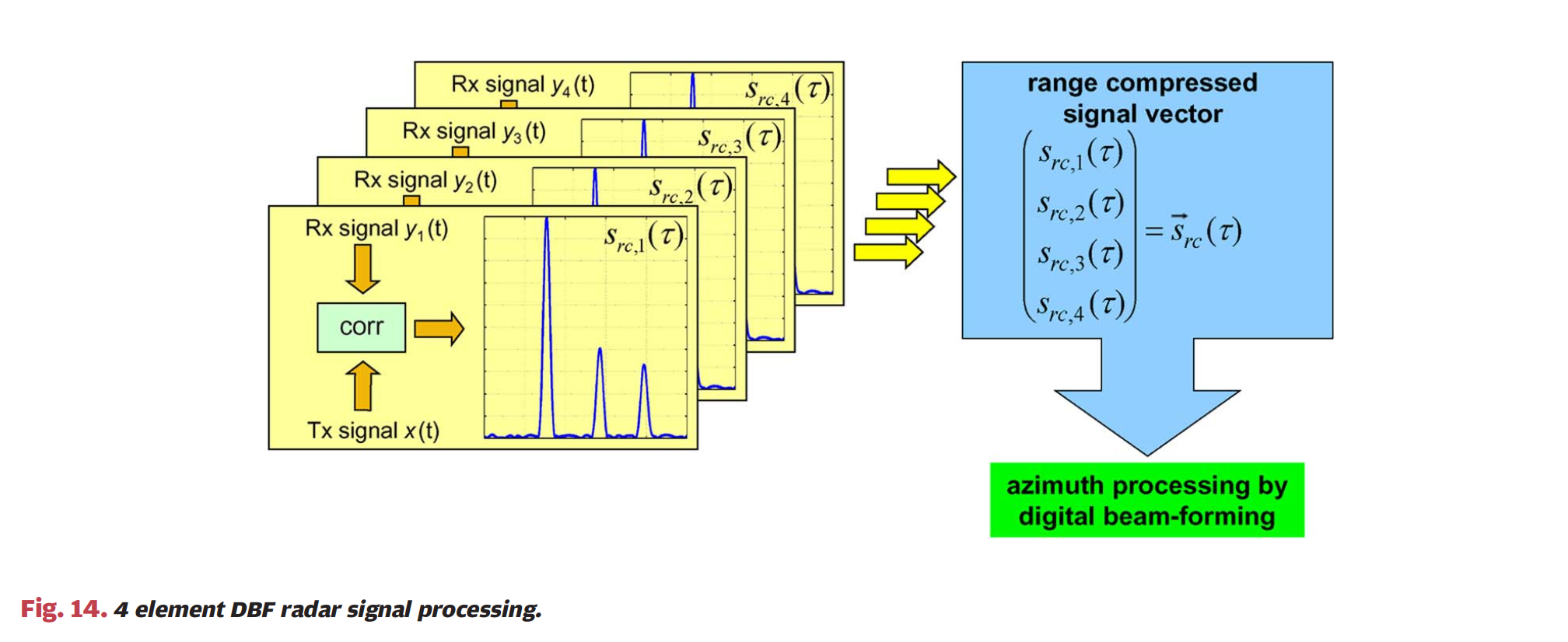
图14 :图14展示了4单元DBF雷达信号处理的示意图。左侧显示发射信号x(t)x(t)x(t)和四个接收信号y1(t)y_1(t)y1(t)到y4(t)y_4(t)y4(t)。每个接收信号首先经过相关器(corr)进行距离压缩,产生距离压缩信号src,1(τ)s_{rc,1}(\tau)src,1(τ)到src,4(τ)s_{rc,4}(\tau)src,4(τ)。这些信号被排列成距离压缩信号向量s⃗rc(τ)\vec{s}_{rc}(\tau)s rc(τ)。然后,该向量被送入"数字波束形成方位处理"模块,执行到达方向估计,最终输出二维雷达图像(距离-方位角)。
对于雷达应用,多天线处理特别有用,因为它允许借助线性天线阵列估计散射物体的方位位置。因此,在随后的讨论中,重点将放在雷达应用的到达方向估计上。然而,相同的方法也可以用于通信应用,在那里它将允许改善信噪比,还可以确定远处发射器的方向。
更一般地,假设接收器有PPP个天线单元的天线阵列,距离压缩预处理器输出信号src(τ)s_{rc}(\tau)src(τ)可以排列成向量:
s⃗rc(τ)=(src,1(τ)src,2(τ)⋮src,P(τ))\vec{s}{rc}(\tau) = \begin{pmatrix} s{rc,1}(\tau) \\ s_{rc,2}(\tau) \\ \vdots \\ s_{rc,P}(\tau) \end{pmatrix}s rc(τ)= src,1(τ)src,2(τ)⋮src,P(τ)
在下文中,将描述和研究两种广泛使用的多天线处理方法的应用。为了限制方程的复杂性,将假设具有恒定单元间距ddd的水平方向线性天线阵列。作为共同基础,两种方法都共享波束导向向量的定义,它是一个描述接收天线位置处复波前样本的向量,假设单个平面波从方位角ψ\psiψ入射到阵列:
b⃗(ψ)=(ejsin(ψ)2πd/λejsin(ψ)2π2d/λ⋮ejsin(ψ)2πPd/λ)\vec{b}(\psi) = \begin{pmatrix} e^{j\sin(\psi)2\pi d/\lambda} \\ e^{j\sin(\psi)2\pi 2d/\lambda} \\ \vdots \\ e^{j\sin(\psi)2\pi Pd/\lambda} \end{pmatrix}b (ψ)= ejsin(ψ)2πd/λejsin(ψ)2π2d/λ⋮ejsin(ψ)2πPd/λ
经典傅里叶变换方法
首先,考虑经典的傅里叶变换方法,该方法简单地将距离压缩信号向量的元素与额外的相移相加。这对应于将距离压缩信号向量与波束导向向量相乘。任何距离τ\tauτ和方位方向ψ\psiψ的雷达图像强度III获得为:
I(τ,ψ)=∣b⃗∗(ψ)s⃗rc(τ)∣2I(\tau, \psi) = |\vec{b}^*(\psi)\vec{s}_{rc}(\tau)|^2I(τ,ψ)=∣b ∗(ψ)s rc(τ)∣2
包括波束导向向量的结构,这可以重写为:
I(τ,ψ)=∣∑p=1Psrc(τ)⋅e−jpu∣2,u=2π⋅dλ⋅sin(ψ)I(\tau, \psi) = \left|\sum_{p=1}^{P} s_{rc}(\tau) \cdot e^{-jpu}\right|^2, \quad u = 2\pi \cdot \frac{d}{\lambda} \cdot \sin(\psi)I(τ,ψ)= p=1∑Psrc(τ)⋅e−jpu 2,u=2π⋅λd⋅sin(ψ)
这正好对应于离散时间傅里叶变换的结构,但在频域中有正弦失真。
MUSIC算法
其次,将考虑一种更复杂的多天线高分辨率处理方法。这种方法被命名为MUSIC(多信号分类),最早被描述于相关文献中。它操作距离压缩信号向量相关矩阵的特征结构。包含Q<PQ < PQ<P个散射体的特定距离单元τ0\tau_0τ0的距离压缩信号向量可以表示为QQQ个波束导向向量的线性组合,每个向量虚拟指向一个单独散射体的方向:
s⃗rc(τ0)=[b⃗(ψ1)⋯b⃗(ψQ)]⋅(a1⋮aQ)+N⃗\vec{s}_{rc}(\tau_0) = [\vec{b}(\psi_1) \quad \cdots \quad \vec{b}(\psi_Q)] \cdot \begin{pmatrix} a_1 \\ \vdots \\ a_Q \end{pmatrix} + \vec{N}s rc(τ0)=[b (ψ1)⋯b (ψQ)]⋅ a1⋮aQ +N
其中a1...aQa_1 \ldots a_Qa1...aQ是不同散射体的复权重,N⃗\vec{N}N 是表示接收天线处加性复噪声值的维度为PPP的向量。由波束导向向量组成的矩阵在下文中将表示为B\mathbf{B}B。计算上式描述的预处理器输出信号向量的相关矩阵Rss\mathbf{R}_{ss}Rss:
Rss=E{s⃗rc(τ0)s⃗rc∗T(τ0)}=BRaaBH+σN2I\mathbf{R}{ss} = E\{\vec{s}{rc}(\tau_0)\vec{s}{rc}^{*T}(\tau_0)\} = \mathbf{B}\mathbf{R}{aa}\mathbf{B}^H + \sigma_N^2\mathbf{I}Rss=E{s rc(τ0)s rc∗T(τ0)}=BRaaBH+σN2I
其中E{}E\{\}E{}表示期望算子,Raa\mathbf{R}_{aa}Raa是复权重a1...aQa_1 \ldots a_Qa1...aQ的相关矩阵,σN2\sigma_N^2σN2是噪声功率,I\mathbf{I}I是维度为PPP的单位矩阵。
深入研究这个结果,可以发现在零噪声功率的情况下,它简化为BRaaBH\mathbf{B}\mathbf{R}{aa}\mathbf{B}^HBRaaBH。这个维度为PPP的矩阵的秩为P−QP-QP−Q,这意味着它有QQQ个非零特征值和P−QP-QP−Q个为零的特征值。如果信号与噪声叠加,在Rss\mathbf{R}{ss}Rss的特征值中仍然存在可区分的差异,有QQQ个由信号和噪声共同影响引起的高特征值e⃗s,i\vec{e}{s,i}e s,i,以及P−QP-QP−Q个仅由噪声引起的相对较小的特征值e⃗n,i\vec{e}{n,i}e n,i。这一特性可以直接用于确定特定距离单元τ0\tau_0τ0中散射体的数量。
对于散射体角度位置的确定,利用了与高特征值和相对较小特征值相关的特征向量所张成的子空间的特定属性。从上式可以推断,组成B\mathbf{B}B且虚拟指向散射体的向量是与Rss\mathbf{R}{ss}Rss的高特征值相关的特征向量e⃗s,i\vec{e}{s,i}e s,i的线性组合。因此,它们必须与Rss\mathbf{R}{ss}Rss的小特征值相关的特征向量e⃗n,i\vec{e}{n,i}e n,i张成的子空间正交。利用这一属性,定义以下雷达图像伪强度:
I(ψ)=1∑i=1P−Q∣b⃗∗(ψ)e⃗n,i∣2I(\psi) = \frac{1}{\sum_{i=1}^{P-Q}|\vec{b}^*(\psi)\vec{e}_{n,i}|^2}I(ψ)=∑i=1P−Q∣b ∗(ψ)e n,i∣21
当满足正交条件时,此表达式将显示强峰,因为分母趋近于零。然而,计算此图像伪强度时获得的结果与散射功率没有直接关系。
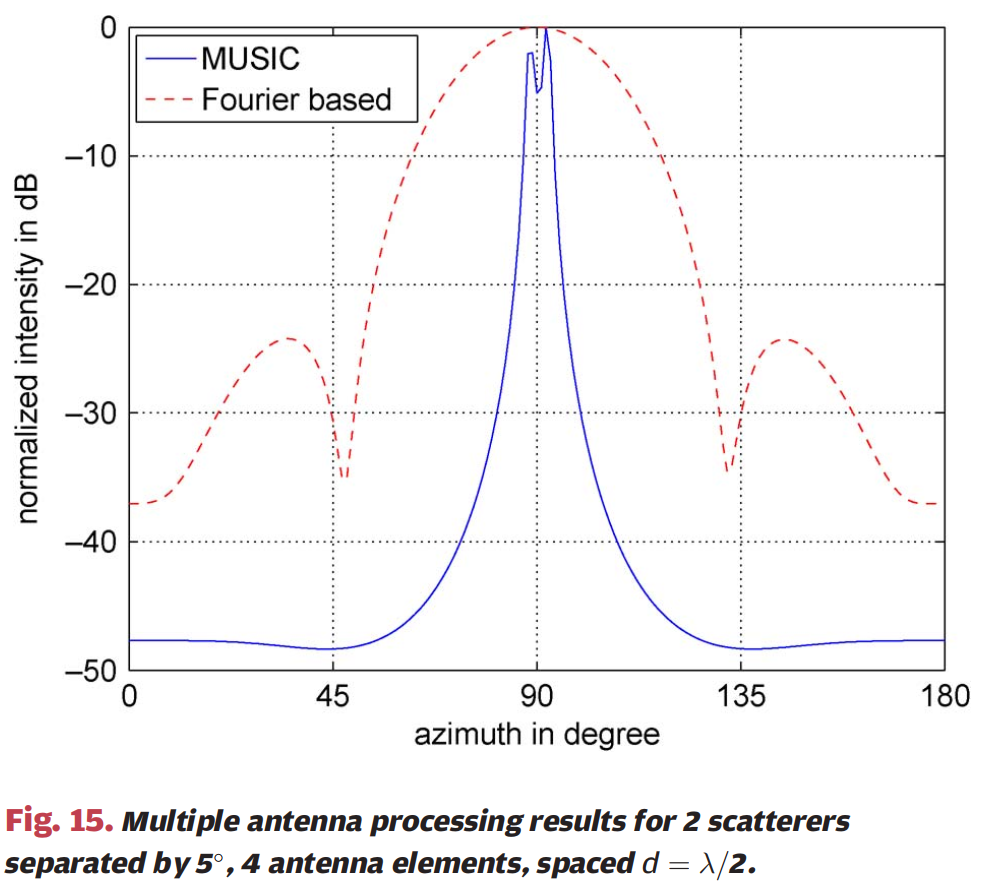
图15 :图15显示了应用两种多天线处理技术与扩频波形结合的示例仿真结果,针对在相同距离处方位角相隔5°的两个点散射体,P=4P=4P=4个接收天线和天线单元间距d=λ/2d=\lambda/2d=λ/2。横轴为方位角(单位:度,从0到180°),纵轴为归一化强度(单位:dB,从0到-50dB)。图中有两条曲线:实线表示MUSIC算法的结果,虚线表示傅里叶方法的结果。首先根据扩频方程执行距离压缩,然后应用两种多天线处理技术。与经典傅里叶变换方法产生非常宽的主瓣而无法区分两个散射体相比,MUSIC算法能够清楚地分离两个散射体(在约88°和93°处显示两个尖锐的峰值)。此外,傅里叶方法显示出相当高的旁瓣(已通过窗口化在处理中降低),而MUSIC算法提供了近50dB的动态范围而没有任何旁瓣。
基于射线追踪的仿真验证
为了更好地了解MUSIC算法在更现实场景中的潜在性能,点散射体模型被专用的基于射线追踪的道路交通环境传播仿真器所取代。除了传播仿真外,该工具还能够基于随机交通模型随机创建典型道路环境的多边形物体模型,包括交通流。在仿真工具中,一辆汽车配备了RadCom系统的发射和接收天线。天线被分配为方位角半功率波束宽度30°、仰角10°的余弦方向图。
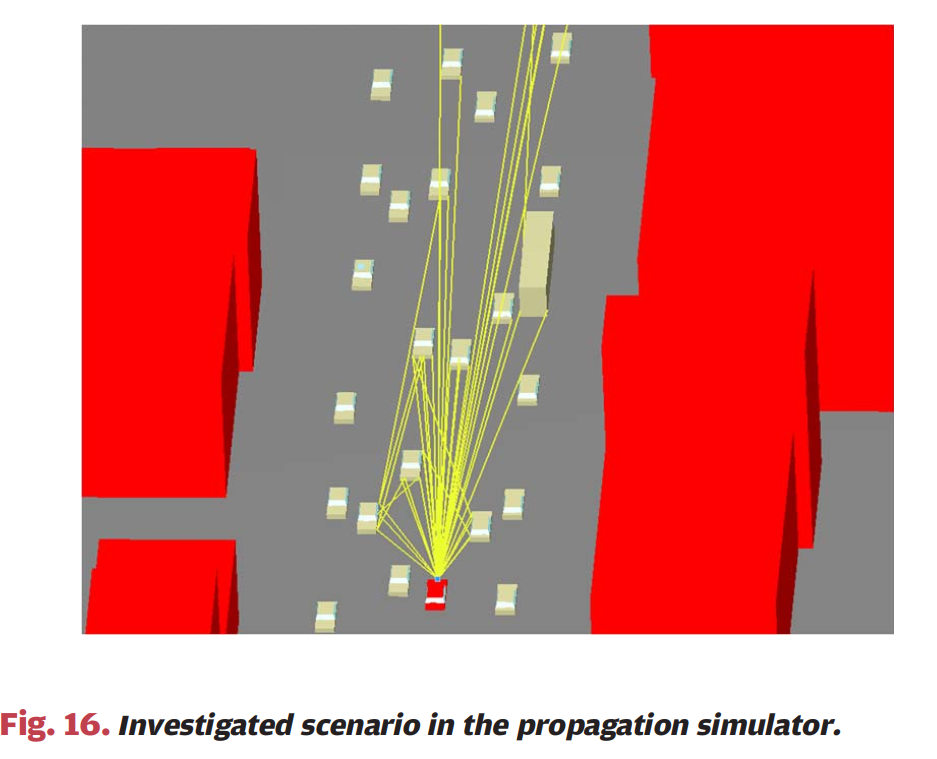
图16:图16显示了在传播仿真器中研究的随机创建场景。这是一个从上方俯瞰的道路场景三维渲染图,显示了多辆汽车在多车道道路上行驶。配备雷达系统的汽车用红色标记。黄色线条表示从发射天线到接收天线的传播路径(包括多次反射的路径),这些路径由射线追踪算法确定。与最强路径相比衰减超过40dB的传播路径不予考虑。对于每条确定的传播路径,单独计算时间延迟、衰减和相移,考虑反射物体的介电材料特性和相关方向下的天线增益,包括完整的极化信息。然后,所有传播路径被相干叠加,以获得瞬时信道脉冲响应。
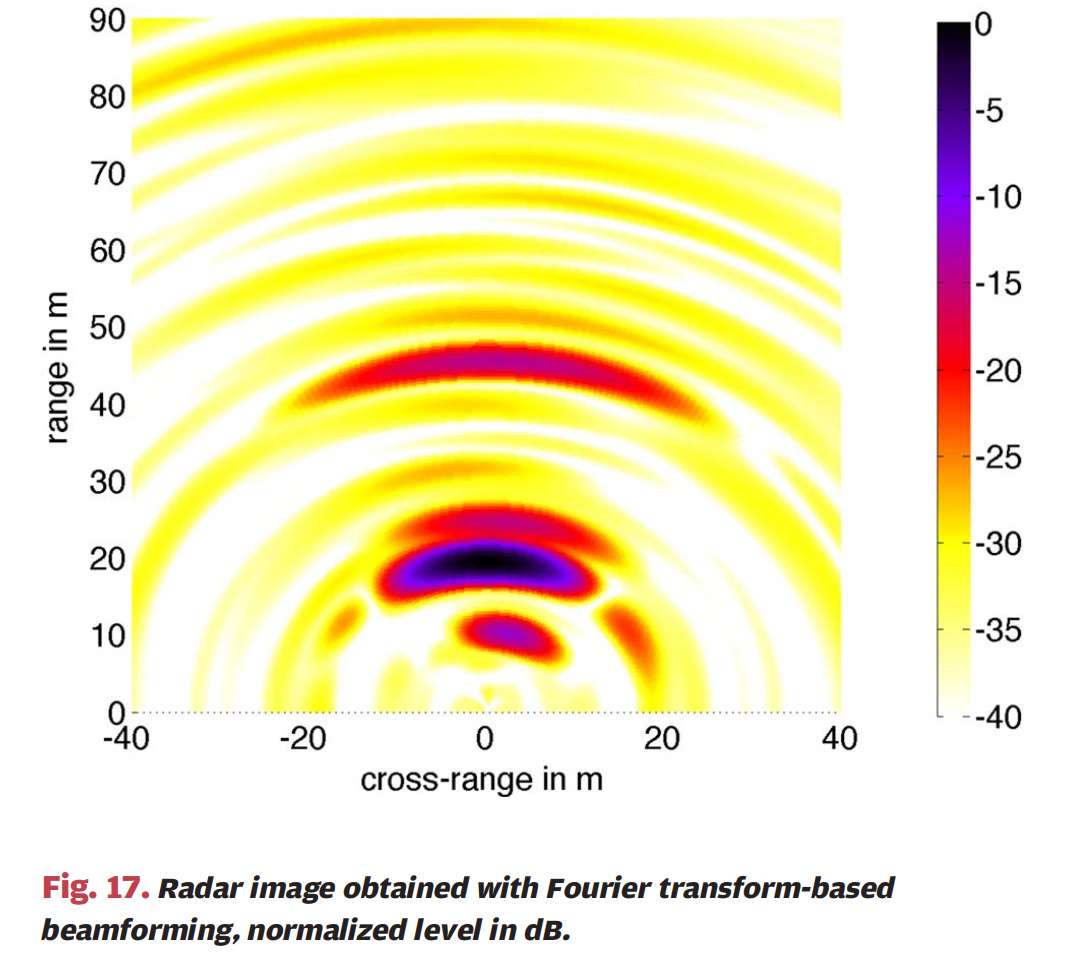
图17:图17显示了使用经典傅里叶变换数字波束形成算法获得的研究场景的雷达图像。横轴为横向距离(单位:米,从-40到40m),纵轴为距离(单位:米,从0到90m),颜色条表示归一化强度(单位:dB,从0到-40dB)。由于接收天线数量少和避免模糊所需的半波长间距,总孔径尺寸小,这只允许较差的角分辨率。只能在雷达图像中检测到四个反射物体。可实现的位置精度相当低。由最强反射引起的旁瓣清晰可见,在图像中形成弧形图案。
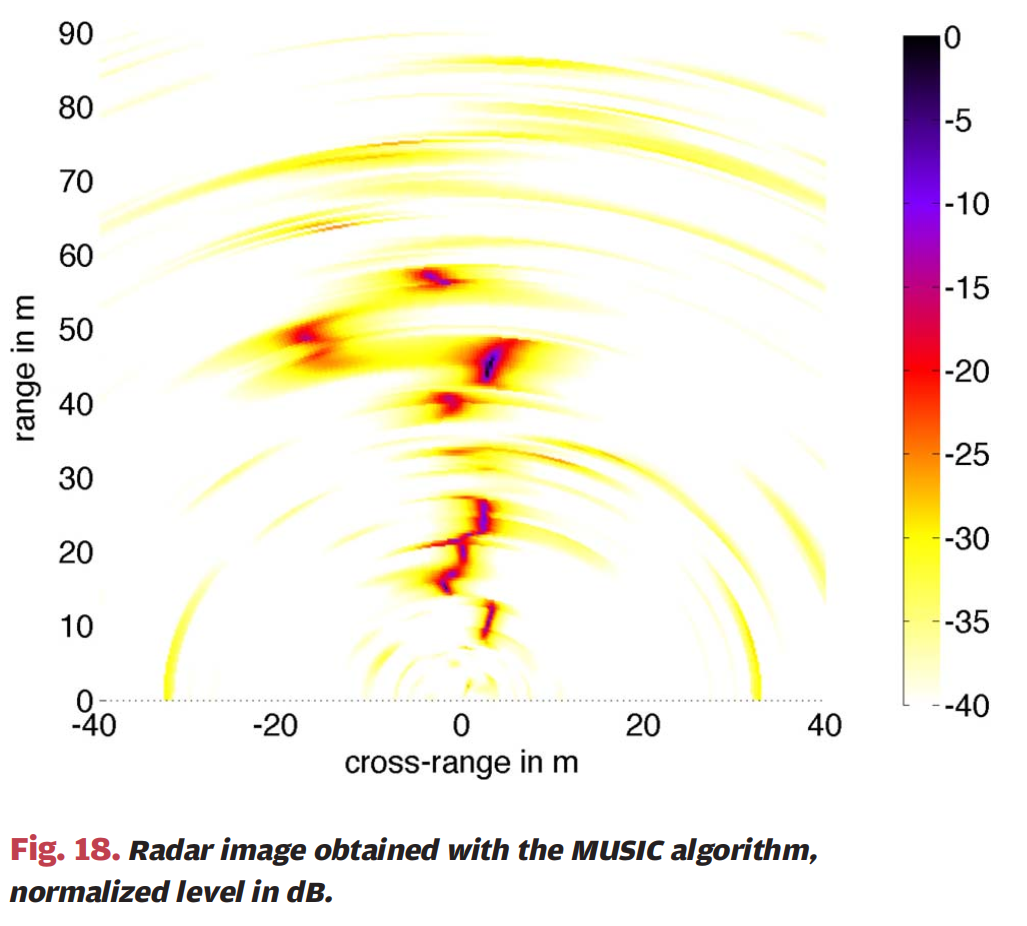
图18:图18显示了使用MUSIC算法获得的相同场景的雷达图像。横轴为横向距离(单位:米,从-40到40m),纵轴为距离(单位:米,从0到90m),颜色条表示归一化强度(单位:dB,从0到-40dB)。使用相同的阵列配置,实现了非常高的角分辨率。当考虑所有-20dB以上的强度值作为反射物体时,至少可以检测到八个反射物体。MUSIC算法的非线性特性放大了雷达图像中较弱的反射,从而简化了目标检测。显然,图16中仅产生低于-40dB阈值反射的所有汽车不会出现在雷达图像中。与傅里叶处理中一样的旁瓣不会出现,背景噪声明显降低。
因此,已经验证所提出的波形设计概念也适合应用多天线处理技术。在仅有四个接收天线的研究系统配置中,MUSIC算法与经典傅里叶方法相比提供了优越的性能。然而,由于需要特征值分解,MUSIC算法带来了更高的复杂性和计算量。
距离性能考虑
下面计算雷达和通信可实现距离的实际示例。通信和雷达应用的性能取决于众多物理和系统相关参数。对于汽车雷达,目前有两个频率在运行,即24和76GHz。在下文中,与前面各章一样,假设载波频率为24GHz。在接收端,噪声系数为NFNFNF,所需的信噪比为SNRsignalSNR_{signal}SNRsignal。在接收天线处,输出SNRsignalSNR_{signal}SNRsignal可能变化很大;根据雷达信号的积分和信息编码,它甚至可能低于0dB。下标Tx和Rx分别表示发射和接收,R表示雷达,C表示通信。天线增益为GGG,带宽为BBB,功率为PPP。由于影响雷达和通信距离的参数数量相当多,将做出某些假设。对于信号衰减的计算,雷达和通信都假设视距传播。
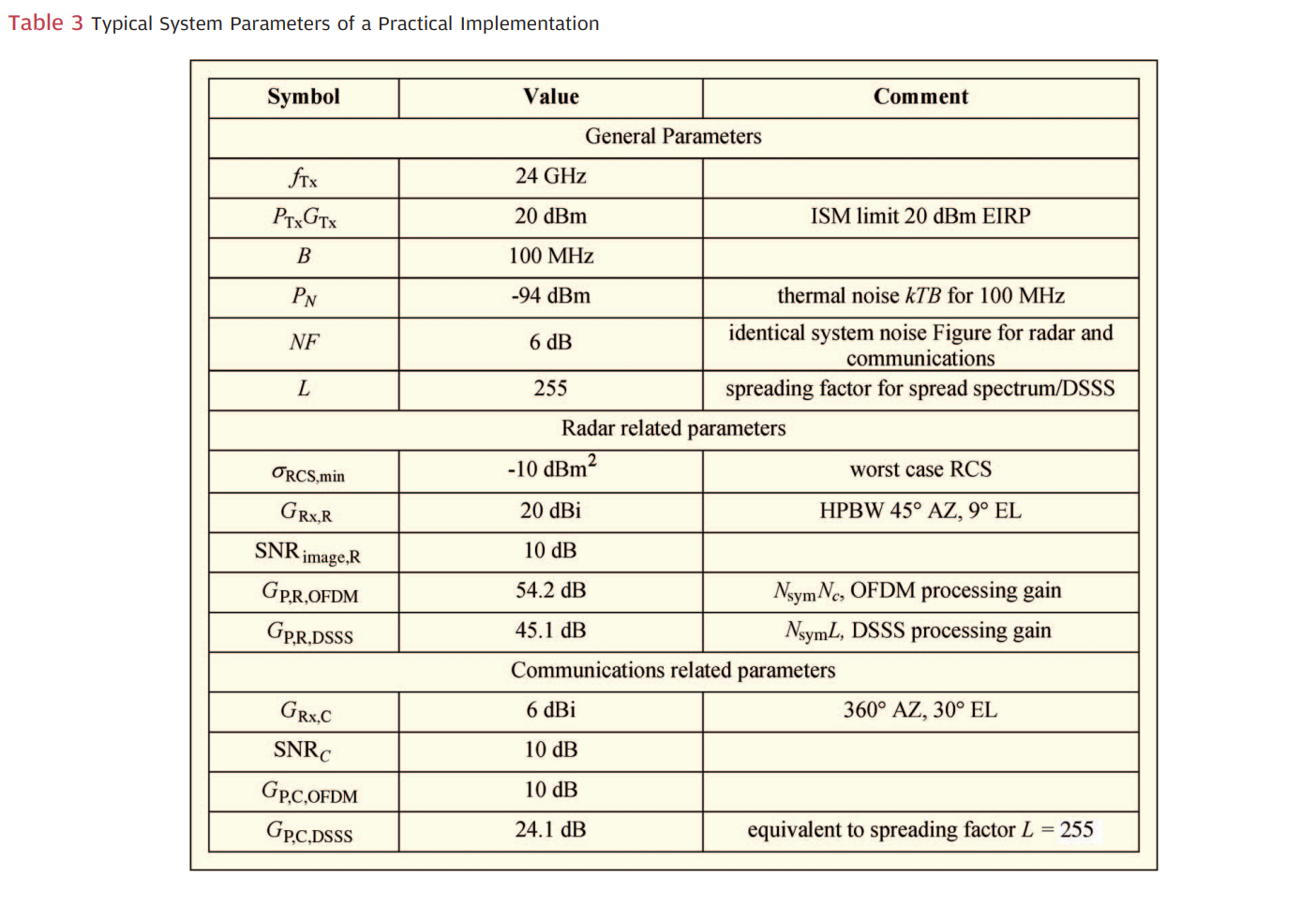
表3 :表3列出了实际实现的典型系统参数。一般参数包括:发射频率fTxf_{Tx}fTx为24GHz;PTxGTxP_{Tx}G_{Tx}PTxGTx为20dBm(ISM限制20dBm EIRP);带宽BBB为100MHz;噪声功率PNP_NPN为-94dBm(100MHz的热噪声kTBkTBkTB);噪声系数NFNFNF为6dB(雷达和通信的相同系统噪声系数);扩频因子LLL为255。雷达相关参数包括:最小雷达截面σRCS,min\sigma_{RCS,min}σRCS,min为-10dBm²(最坏情况RCS);接收天线增益GRx,RG_{Rx,R}GRx,R为20dBi(半功率波束宽度45°方位角、9°仰角);雷达图像信噪比SNRimage,RSNR_{image,R}SNRimage,R为10dB;OFDM处理增益GP,R,OFDMG_{P,R,OFDM}GP,R,OFDM为54.2dB(NsymNcN_{sym}N_cNsymNc);DSSS处理增益GP,R,DSSSG_{P,R,DSSS}GP,R,DSSS为45.1dB(NsymLN_{sym}LNsymL)。通信相关参数包括:接收天线增益GRx,CG_{Rx,C}GRx,C为6dBi(360°方位角、30°仰角);通信信噪比SNRCSNR_CSNRC为10dB;OFDM通信处理增益GP,C,OFDMG_{P,C,OFDM}GP,C,OFDM为10dB;DSSS通信处理增益GP,C,DSSSG_{P,C,DSSS}GP,C,DSSS为24.1dB(等效于扩频因子L=255L=255L=255)。
OFDM系统假设的10dB通信处理增益来自冗余编码的应用,同时将QPSK调制的最大可能数据速率从200降低到20Mb/s。对于DSSS,通信处理增益对应于扩频因子,也将数据速率从100Mb/s的码片速率降低到392kb/s。
对于雷达应用,接收信号功率用雷达方程计算:
PRx,R=PTxGTxGRx,RσRCSλ2(4π)3RR4P_{Rx,R} = \frac{P_{Tx}G_{Tx}G_{Rx,R}\sigma_{RCS}\lambda^2}{(4\pi)^3R_R^4}PRx,R=(4π)3RR4PTxGTxGRx,RσRCSλ2
其中σRCS\sigma_{RCS}σRCS是反射物体的雷达截面,λ\lambdaλ是与载波频率相关的波长,RRR_RRR是雷达平台与反射物体之间的距离。对于通信应用,接收信号功率由自由空间传播定律得出:
PRx,C=PTxGTxGRx,Cλ2(4π)2RC2P_{Rx,C} = \frac{P_{Tx}G_{Tx}G_{Rx,C}\lambda^2}{(4\pi)^2R_C^2}PRx,C=(4π)2RC2PTxGTxGRx,Cλ2
其中RCR_CRC表示发射器和接收器之间的距离。对于SNR的计算,必须考虑热噪声功率和接收器噪声系数NFNFNF:
SNR=PRxPNNF=PRxkBTabsNFSNR = \frac{P_{Rx}}{P_NNF} = \frac{P_{Rx}}{kBT_{abs}NF}SNR=PNNFPRx=kBTabsNFPRx
其中kkk是玻尔兹曼常数,TabsT_{abs}Tabs是绝对温度。
在性能计算中,必须考虑到通信和雷达操作都可获得处理增益GPG_PGP。雷达操作的最大距离由上述方程得出:
Rmax,R=PTxGTxGRx,RGP,Rσλ2PN⋅NFR⋅SNRimage,R⋅(4π)34R_{max,R} = \sqrt[4]{\frac{P_{Tx}G_{Tx}G_{Rx,R}G_{P,R}\sigma\lambda^2}{P_N \cdot NF_R \cdot SNR_{image,R} \cdot (4\pi)^3}}Rmax,R=4PN⋅NFR⋅SNRimage,R⋅(4π)3PTxGTxGRx,RGP,Rσλ2
通信的最大距离为:
Rmax,C=PTxGTxGRx,CGP,Cλ2PN⋅NFC⋅SNRC⋅(4π)2R_{max,C} = \sqrt{\frac{P_{Tx}G_{Tx}G_{Rx,C}G_{P,C}\lambda^2}{P_N \cdot NF_C \cdot SNR_C \cdot (4\pi)^2}}Rmax,C=PN⋅NFC⋅SNRC⋅(4π)2PTxGTxGRx,CGP,Cλ2
从上述方程,距离比较如下:
Rmax,CRmax,R=GRx,CGP,CλNFCSNRCPNPTxGTxNFRSNRimage,R4π⋅PNGRx,RGP,Rσ4\frac{R_{max,C}}{R_{max,R}} = \sqrt{\frac{G_{Rx,C}G_{P,C}\lambda}{NF_CSNR_CP_N}} \sqrt[4]{\frac{P_{Tx}G_{Tx}NF_RSNR_{image,R}4\pi \cdot P_N}{G_{Rx,R}G_{P,R}\sigma}}Rmax,RRmax,C=NFCSNRCPNGRx,CGP,Cλ 4GRx,RGP,RσPTxGTxNFRSNRimage,R4π⋅PN

表4 :表4总结了DSSS和OFDM编码RadCom系统的距离比较结果。对于DSSS调制:雷达距离为112m,通信距离为2512m,数据速率为392kbit/s,Rmax,C/Rmax,RR_{max,C}/R_{max,R}Rmax,C/Rmax,R为22.4。对于OFDM调制:雷达距离为190m,通信距离为495m,数据速率为20Mbit/s,Rmax,C/Rmax,RR_{max,C}/R_{max,R}Rmax,C/Rmax,R为2.61。
从表4可以看出,两种概念都提供了适合实际应用的雷达和通信性能。由于相应更高的雷达处理增益,OFDM调制实现了更高的雷达距离。对于汽车应用,理想情况下雷达距离应为250m。这需要对示例参数进行一些更改。可以为特殊应用改变的参数包括带宽BBB、积分持续时间(处理增益)、硬件系统参数GTxG_{Tx}GTx、GRxG_{Rx}GRx、PTxP_{Tx}PTx或噪声系数NFNFNF。DSSS具有降低的雷达距离,但它也表现出更高的通信距离。尽管如此,考虑到相当高的用户数据速率,OFDM概念似乎在所有性能标准中提供了更好的权衡。
结论
目前,移动通信的想法基于特定分配频谱的可用性,例如5.9GHz。但是,众所周知,24GHz和76GHz有更宽的频谱可用于汽车雷达。本文已经表明,这些雷达频谱可以用信息编码,而不会对雷达性能产生任何负面影响。另一方面,通过本文提出的概念,5.9GHz频段的车对车通信系统可以配备额外的雷达功能。
研究了两种不同的波形设计概念,允许同时进行无线通信和雷达操作:OFDM和DSSS。两种方法的可操作性和性能都得到了全面评估。使用多载波信号(OFDM)的实现已被证明在雷达应用性能方面提供了许多优势,特别是非常高的动态范围、独立于发射用户数据、估计相对速度的可能性以及基于快速傅里叶变换的高效实现。另一方面,扩频方法(DSSS)便于通信应用中多用户的分离。OFDM方法在实际道路场景中的可操作性已通过专用系统演示器得到验证。
还表明,具有到达方向估计处理技术的多天线接收器得到了这些波形的良好支持。对于角度聚焦,除了经典的傅里叶方法外,还发现MUSIC算法能够仅用四个接收天线提供高角分辨率。可以得出结论,所讨论的波形设计和信号处理概念为实现未来智能传感器设备提供了有趣的前景,这些设备使用一个共同的信号联合执行频谱高效的雷达感知和通信,并以一个共同的硬件系统进行经济高效的实现。
附录A:扩频雷达相关处理的推导
A.1 相关函数的完整推导
考虑扩频编码后的发射信号:
x(t)=∑i=0LNsym−1c(i)g(t−iT)x(t) = \sum_{i=0}^{LN_{sym}-1} c(i)g(t - iT)x(t)=i=0∑LNsym−1c(i)g(t−iT)
其中c(i)c(i)c(i)是扩频编码后的符号序列,g(t)g(t)g(t)是基带脉冲形状,TTT是符号持续时间。
当信号从距离RRR处的物体反射时,接收信号为:
y(t)=Ax(t−2Rc0)=A∑i=0LNsym−1c(i)g(t−2Rc0−iT)y(t) = Ax\left(t - \frac{2R}{c_0}\right) = A\sum_{i=0}^{LN_{sym}-1} c(i)g\left(t - \frac{2R}{c_0} - iT\right)y(t)=Ax(t−c02R)=Ai=0∑LNsym−1c(i)g(t−c02R−iT)
互相关函数定义为:
ryx(τ)=∫−∞∞y(t)x∗(t−τ)dtr_{yx}(\tau) = \int_{-\infty}^{\infty} y(t)x^*(t-\tau)dtryx(τ)=∫−∞∞y(t)x∗(t−τ)dt
将y(t)y(t)y(t)和x(t)x(t)x(t)代入:
ryx(τ)=∫−∞∞[A∑i=0LNsym−1c(i)g(t−2Rc0−iT)][∑k=0LNsym−1c∗(k)g∗(t−τ−kT)]dtr_{yx}(\tau) = \int_{-\infty}^{\infty} \left[A\sum_{i=0}^{LN_{sym}-1} c(i)g\left(t - \frac{2R}{c_0} - iT\right)\right] \left[\sum_{k=0}^{LN_{sym}-1} c^*(k)g^*(t - \tau - kT)\right]dtryx(τ)=∫−∞∞ Ai=0∑LNsym−1c(i)g(t−c02R−iT) k=0∑LNsym−1c∗(k)g∗(t−τ−kT) dt
由于积分的线性性,可以交换积分和求和的顺序:
ryx(τ)=A∑i=0LNsym−1∑k=0LNsym−1c(i)c∗(k)∫−∞∞g(t−2Rc0−iT)g∗(t−τ−kT)dtr_{yx}(\tau) = A\sum_{i=0}^{LN_{sym}-1} \sum_{k=0}^{LN_{sym}-1} c(i)c^*(k) \int_{-\infty}^{\infty} g\left(t - \frac{2R}{c_0} - iT\right)g^*(t - \tau - kT)dtryx(τ)=Ai=0∑LNsym−1k=0∑LNsym−1c(i)c∗(k)∫−∞∞g(t−c02R−iT)g∗(t−τ−kT)dt
定义脉冲形状的自相关函数:
rgg(Δ)=∫−∞∞g(t)g∗(t−Δ)dtr_{gg}(\Delta) = \int_{-\infty}^{\infty} g(t)g^*(t - \Delta)dtrgg(Δ)=∫−∞∞g(t)g∗(t−Δ)dt
通过变量替换t′=t−2Rc0−iTt' = t - \frac{2R}{c_0} - iTt′=t−c02R−iT,积分变为:
∫−∞∞g(t′)g∗(t′+2Rc0+iT−τ−kT)dt′=rgg(τ−2Rc0−(i−k)T)\int_{-\infty}^{\infty} g(t')g^*\left(t' + \frac{2R}{c_0} + iT - \tau - kT\right)dt' = r_{gg}\left(\tau - \frac{2R}{c_0} - (i-k)T\right)∫−∞∞g(t′)g∗(t′+c02R+iT−τ−kT)dt′=rgg(τ−c02R−(i−k)T)
因此:
ryx(τ)=A∑i=0LNsym−1∑k=0LNsym−1c(i)c∗(k)rgg(τ−2Rc0+(k−i)T)r_{yx}(\tau) = A\sum_{i=0}^{LN_{sym}-1} \sum_{k=0}^{LN_{sym}-1} c(i)c^*(k)r_{gg}\left(\tau - \frac{2R}{c_0} + (k-i)T\right)ryx(τ)=Ai=0∑LNsym−1k=0∑LNsym−1c(i)c∗(k)rgg(τ−c02R+(k−i)T)
A.2 峰值条件分析
对于根升余弦滤波器,rgg(τ)r_{gg}(\tau)rgg(τ)在τ=0\tau = 0τ=0时达到最大值。要使ryx(τ)r_{yx}(\tau)ryx(τ)产生主峰,需要满足两个条件:
条件1(脉冲自相关峰值) :rggr_{gg}rgg的参数为零,即:
τ−2Rc0+(k−i)T=0\tau - \frac{2R}{c_0} + (k-i)T = 0τ−c02R+(k−i)T=0
条件2(码序列相干叠加) :c(i)c(i)c(i)和c(k)c(k)c(k)相干叠加,当k=i+mk = i + mk=i+m时(其中mmm是整数),自相关为:
∑ic(i)c∗(i+m)=rcc(m)\sum_{i} c(i)c^*(i+m) = r_{cc}(m)i∑c(i)c∗(i+m)=rcc(m)
对于理想的伪随机序列,rcc(0)=Lr_{cc}(0) = Lrcc(0)=L(序列长度),而rcc(m≠0)≈0r_{cc}(m \neq 0) \approx 0rcc(m=0)≈0。
联立两个条件,当τ=0\tau = 0τ=0时:
k=i+⌊2Rc0T⌋k = i + \left\lfloor\frac{2R}{c_0T}\right\rfloork=i+⌊c0T2R⌋
这给出了与目标距离RRR对应的索引偏移。
A.3 Welch界的物理意义
Welch界给出了互相关和自相关旁瓣的联合下界:
max{∣rcc(i≠0)∣,∣rc1c2(i)∣}≥L2(M−1)LM−1\max\{|r_{cc}(i \neq 0)|, |r_{c_1c_2}(i)|\} \geq \sqrt{\frac{L^2(M-1)}{LM-1}}max{∣rcc(i=0)∣,∣rc1c2(i)∣}≥LM−1L2(M−1)
当M≫1M \gg 1M≫1且L≫1L \gg 1L≫1时,此界近似为:
max{∣rcc(i≠0)∣,∣rc1c2(i)∣}≳L\max\{|r_{cc}(i \neq 0)|, |r_{c_1c_2}(i)|\} \gtrsim \sqrt{L}max{∣rcc(i=0)∣,∣rc1c2(i)∣}≳L
而自相关峰值为LLL,因此峰值旁瓣比的理论上界为:
PSLmax≈20log10(LL)=10log10(L) dBPSL_{max} \approx 20\log_{10}\left(\frac{L}{\sqrt{L}}\right) = 10\log_{10}(L) \text{ dB}PSLmax≈20log10(L L)=10log10(L) dB
对于L=255L = 255L=255,理论PSL上界约为24dB,这与仿真结果一致。
附录B:OFDM雷达调制符号域处理的推导
B.1 接收信号模型的完整推导
OFDM发射信号的基带表示为:
x(t)=∑μ=0Nsym−1∑n=0Nc−1dTx(μ,n)ej2πfntrect(t−μTOFDMTOFDM)x(t) = \sum_{\mu=0}^{N_{sym}-1} \sum_{n=0}^{N_c-1} d_{Tx}(\mu, n) e^{j2\pi f_n t} \text{rect}\left(\frac{t - \mu T_{OFDM}}{T_{OFDM}}\right)x(t)=μ=0∑Nsym−1n=0∑Nc−1dTx(μ,n)ej2πfntrect(TOFDMt−μTOFDM)
其中fn=nΔf=n/Tf_n = n\Delta f = n/Tfn=nΔf=n/T是第nnn个子载波的频率。
当信号从距离RRR、相对速度vrelv_{rel}vrel的物体反射时,时间延迟为τd=2R/c0\tau_d = 2R/c_0τd=2R/c0,多普勒频移为fD=2vrelfc/c0f_D = 2v_{rel}f_c/c_0fD=2vrelfc/c0。接收信号为:
y(t)=A⋅x(t−τd)⋅ej2πfDty(t) = A \cdot x(t - \tau_d) \cdot e^{j2\pi f_D t}y(t)=A⋅x(t−τd)⋅ej2πfDt
代入x(t)x(t)x(t)的表达式:
y(t)=A∑μ=0Nsym−1∑n=0Nc−1dTx(μ,n)ej2πfn(t−τd)ej2πfDtrect(t−τd−μTOFDMTOFDM)y(t) = A\sum_{\mu=0}^{N_{sym}-1} \sum_{n=0}^{N_c-1} d_{Tx}(\mu, n) e^{j2\pi f_n (t-\tau_d)} e^{j2\pi f_D t} \text{rect}\left(\frac{t - \tau_d - \mu T_{OFDM}}{T_{OFDM}}\right)y(t)=Aμ=0∑Nsym−1n=0∑Nc−1dTx(μ,n)ej2πfn(t−τd)ej2πfDtrect(TOFDMt−τd−μTOFDM)
B.2 接收调制符号的提取
OFDM接收器通过FFT从接收信号中提取调制符号。对于第μ\muμ个OFDM符号的第nnn个子载波,接收调制符号通过以下积分获得:
dRx(μ,n)=1T∫μTOFDM+TG(μ+1)TOFDMy(t)e−j2πfntdtd_{Rx}(\mu, n) = \frac{1}{T}\int_{\mu T_{OFDM} + T_G}^{(\mu+1)T_{OFDM}} y(t) e^{-j2\pi f_n t} dtdRx(μ,n)=T1∫μTOFDM+TG(μ+1)TOFDMy(t)e−j2πfntdt
假设保护间隔TGT_GTG足够长以容纳时间延迟τd\tau_dτd,代入y(t)y(t)y(t):
dRx(μ,n)=AT∫μTOFDM+TG(μ+1)TOFDM∑n′=0Nc−1dTx(μ,n′)ej2πfn′(t−τd)ej2πfDte−j2πfntdtd_{Rx}(\mu, n) = \frac{A}{T}\int_{\mu T_{OFDM} + T_G}^{(\mu+1)T_{OFDM}} \sum_{n'=0}^{N_c-1} d_{Tx}(\mu, n') e^{j2\pi f_{n'} (t-\tau_d)} e^{j2\pi f_D t} e^{-j2\pi f_n t} dtdRx(μ,n)=TA∫μTOFDM+TG(μ+1)TOFDMn′=0∑Nc−1dTx(μ,n′)ej2πfn′(t−τd)ej2πfDte−j2πfntdt
由于子载波正交性,只有n′=nn' = nn′=n的项贡献非零值:
dRx(μ,n)=A⋅dTx(μ,n)⋅e−j2πfnτd⋅ej2πfDμTOFDMd_{Rx}(\mu, n) = A \cdot d_{Tx}(\mu, n) \cdot e^{-j2\pi f_n \tau_d} \cdot e^{j2\pi f_D \mu T_{OFDM}}dRx(μ,n)=A⋅dTx(μ,n)⋅e−j2πfnτd⋅ej2πfDμTOFDM
代入fn=nΔff_n = n\Delta ffn=nΔf、τd=2R/c0\tau_d = 2R/c_0τd=2R/c0和fD=2vrelfc/c0f_D = 2v_{rel}f_c/c_0fD=2vrelfc/c0:
dRx(μ,n)=A⋅dTx(μ,n)⋅exp(−j2πnΔf2Rc0)⋅exp(j2πμTOFDM2vrelfcc0)d_{Rx}(\mu, n) = A \cdot d_{Tx}(\mu, n) \cdot \exp\left(-j2\pi n\Delta f\frac{2R}{c_0}\right) \cdot \exp\left(j2\pi\mu T_{OFDM}\frac{2v_{rel}f_c}{c_0}\right)dRx(μ,n)=A⋅dTx(μ,n)⋅exp(−j2πnΔfc02R)⋅exp(j2πμTOFDMc02vrelfc)
B.3 距离-多普勒分离的正交性证明
定义相位项:
ϕR(n)=−2πnΔf2Rc0\phi_R(n) = -2\pi n\Delta f\frac{2R}{c_0}ϕR(n)=−2πnΔfc02R
ϕD(μ)=2πμTOFDM2vrelfcc0\phi_D(\mu) = 2\pi\mu T_{OFDM}\frac{2v_{rel}f_c}{c_0}ϕD(μ)=2πμTOFDMc02vrelfc
接收调制符号可以写为:
dRx(μ,n)=A⋅dTx(μ,n)⋅ejϕR(n)⋅ejϕD(μ)d_{Rx}(\mu, n) = A \cdot d_{Tx}(\mu, n) \cdot e^{j\phi_R(n)} \cdot e^{j\phi_D(\mu)}dRx(μ,n)=A⋅dTx(μ,n)⋅ejϕR(n)⋅ejϕD(μ)
关键观察:
- ϕR(n)\phi_R(n)ϕR(n)仅依赖于子载波索引nnn,与OFDM符号索引μ\muμ无关
- ϕD(μ)\phi_D(\mu)ϕD(μ)仅依赖于OFDM符号索引μ\muμ,与子载波索引nnn无关
这意味着在调制符号矩阵中,距离引起的相移仅沿频率轴(行方向)变化,而多普勒引起的相移仅沿时间轴(列方向)变化。两者是完全正交和可分离的。
B.4 二维FFT处理的数学基础
执行元素除法后:
ddiv(μ,n)=dRx(μ,n)dTx(μ,n)=A⋅ejϕR(n)⋅ejϕD(μ)d_{div}(\mu, n) = \frac{d_{Rx}(\mu, n)}{d_{Tx}(\mu, n)} = A \cdot e^{j\phi_R(n)} \cdot e^{j\phi_D(\mu)}ddiv(μ,n)=dTx(μ,n)dRx(μ,n)=A⋅ejϕR(n)⋅ejϕD(μ)
这可以写成两个向量的外积:
Ddiv=A⋅k⃗R⊗k⃗D\mathbf{D}_{div} = A \cdot \vec{k}_R \otimes \vec{k}_DDdiv=A⋅k R⊗k D
其中:
k⃗R=[ejϕR(0),ejϕR(1),...,ejϕR(Nc−1)]T\vec{k}_R = [e^{j\phi_R(0)}, e^{j\phi_R(1)}, \ldots, e^{j\phi_R(N_c-1)}]^Tk R=[ejϕR(0),ejϕR(1),...,ejϕR(Nc−1)]T
k⃗D=[ejϕD(0),ejϕD(1),...,ejϕD(Nsym−1)]\vec{k}D = [e^{j\phi_D(0)}, e^{j\phi_D(1)}, \ldots, e^{j\phi_D(N{sym}-1)}]k D=[ejϕD(0),ejϕD(1),...,ejϕD(Nsym−1)]
沿频率轴的IDFT(距离估计):
r(k)=∑n=0Nc−1ejϕR(n)ej2πnkNc=∑n=0Nc−1exp[jn(2πkNc−2πΔf2Rc0)]r(k) = \sum_{n=0}^{N_c-1} e^{j\phi_R(n)} e^{j\frac{2\pi nk}{N_c}} = \sum_{n=0}^{N_c-1} \exp\left[jn\left(\frac{2\pi k}{N_c} - 2\pi\Delta f\frac{2R}{c_0}\right)\right]r(k)=n=0∑Nc−1ejϕR(n)ejNc2πnk=n=0∑Nc−1exp[jn(Nc2πk−2πΔfc02R)]
当相位项为零时,即:
2πkNc=2πΔf2Rc0\frac{2\pi k}{N_c} = 2\pi\Delta f\frac{2R}{c_0}Nc2πk=2πΔfc02R
解得:
k=2RΔfNcc0=2RNcc0T=2RBc0k = \frac{2R\Delta f N_c}{c_0} = \frac{2RN_c}{c_0 T} = \frac{2RB}{c_0}k=c02RΔfNc=c0T2RNc=c02RB
其中使用了B=NcΔfB = N_c\Delta fB=NcΔf。此时所有NcN_cNc个项相干相加,产生峰值∣r(k)∣=Nc|r(k)| = N_c∣r(k)∣=Nc。
沿时间轴的DFT(多普勒估计):
v(l)=∑μ=0Nsym−1ejϕD(μ)e−j2πμlNsym=∑μ=0Nsym−1exp[jμ(2πTOFDM2vrelfcc0−2πlNsym)]v(l) = \sum_{\mu=0}^{N_{sym}-1} e^{j\phi_D(\mu)} e^{-j\frac{2\pi \mu l}{N_{sym}}} = \sum_{\mu=0}^{N_{sym}-1} \exp\left[j\mu\left(2\pi T_{OFDM}\frac{2v_{rel}f_c}{c_0} - \frac{2\pi l}{N_{sym}}\right)\right]v(l)=μ=0∑Nsym−1ejϕD(μ)e−jNsym2πμl=μ=0∑Nsym−1exp[jμ(2πTOFDMc02vrelfc−Nsym2πl)]
当相位项为零时:
l=2vrelfcTOFDMNsymc0l = \frac{2v_{rel}f_c T_{OFDM} N_{sym}}{c_0}l=c02vrelfcTOFDMNsym
此时所有NsymN_{sym}Nsym个项相干相加,产生峰值∣v(l)∣=Nsym|v(l)| = N_{sym}∣v(l)∣=Nsym。
B.5 处理增益的推导
考虑加性高斯白噪声w(μ,n)w(\mu, n)w(μ,n),接收信号变为:
dRx(μ,n)=A⋅dTx(μ,n)⋅ejϕR(n)⋅ejϕD(μ)+w(μ,n)d_{Rx}(\mu, n) = A \cdot d_{Tx}(\mu, n) \cdot e^{j\phi_R(n)} \cdot e^{j\phi_D(\mu)} + w(\mu, n)dRx(μ,n)=A⋅dTx(μ,n)⋅ejϕR(n)⋅ejϕD(μ)+w(μ,n)
元素除法后(假设∣dTx∣=1|d_{Tx}| = 1∣dTx∣=1):
ddiv(μ,n)=A⋅ejϕR(n)⋅ejϕD(μ)+w(μ,n)dTx(μ,n)d_{div}(\mu, n) = A \cdot e^{j\phi_R(n)} \cdot e^{j\phi_D(\mu)} + \frac{w(\mu, n)}{d_{Tx}(\mu, n)}ddiv(μ,n)=A⋅ejϕR(n)⋅ejϕD(μ)+dTx(μ,n)w(μ,n)
由于∣dTx∣=1|d_{Tx}| = 1∣dTx∣=1,噪声项保持相同的统计特性。
二维FFT后,信号项的峰值功率为(NcNsym)2∣A∣2(N_c N_{sym})^2 |A|^2(NcNsym)2∣A∣2(因为NcNsymN_c N_{sym}NcNsym个相位相干项相加)。噪声项由于其随机性,功率增益为NcNsymN_c N_{sym}NcNsym(非相干叠加)。
因此,处理增益为:
GP=(NcNsym)2NcNsym=NcNsymG_P = \frac{(N_c N_{sym})^2}{N_c N_{sym}} = N_c N_{sym}GP=NcNsym(NcNsym)2=NcNsym
对于表2中的参数,GP=1024×256=262144G_P = 1024 \times 256 = 262144GP=1024×256=262144,对应10log10(262144)≈54.210\log_{10}(262144) \approx 54.210log10(262144)≈54.2 dB。
附录C:MUSIC算法的数学推导
C.1 信号模型
考虑PPP个天线单元的均匀线性阵列,接收来自Q<PQ < PQ<P个方向的信号。第ppp个天线的接收信号为:
xp(t)=∑q=1Qsq(t)ej(p−1)ψq+np(t)x_p(t) = \sum_{q=1}^{Q} s_q(t) e^{j(p-1)\psi_q} + n_p(t)xp(t)=q=1∑Qsq(t)ej(p−1)ψq+np(t)
其中ψq=2πdsinθq/λ\psi_q = 2\pi d\sin\theta_q/\lambdaψq=2πdsinθq/λ是第qqq个源的相位延迟,sq(t)s_q(t)sq(t)是信号,np(t)n_p(t)np(t)是噪声。
向量形式:
x⃗(t)=Bs⃗(t)+n⃗(t)\vec{x}(t) = \mathbf{B}\vec{s}(t) + \vec{n}(t)x (t)=Bs (t)+n (t)
其中B=[b⃗(θ1),...,b⃗(θQ)]\mathbf{B} = [\vec{b}(\theta_1), \ldots, \vec{b}(\theta_Q)]B=[b (θ1),...,b (θQ)]是P×QP \times QP×Q的导向矩阵,b⃗(θq)=[1,ejψq,...,ej(P−1)ψq]T\vec{b}(\theta_q) = [1, e^{j\psi_q}, \ldots, e^{j(P-1)\psi_q}]^Tb (θq)=[1,ejψq,...,ej(P−1)ψq]T。
C.2 相关矩阵分析
信号相关矩阵:
Rxx=E[x⃗(t)x⃗H(t)]=BRssBH+σn2I\mathbf{R}{xx} = E[\vec{x}(t)\vec{x}^H(t)] = \mathbf{B}\mathbf{R}{ss}\mathbf{B}^H + \sigma_n^2\mathbf{I}Rxx=E[x (t)x H(t)]=BRssBH+σn2I
其中Rss=E[s⃗(t)s⃗H(t)]\mathbf{R}_{ss} = E[\vec{s}(t)\vec{s}^H(t)]Rss=E[s (t)s H(t)]是源信号相关矩阵。
C.3 特征分解
设Rxx\mathbf{R}_{xx}Rxx的特征值为λ1≥λ2≥...≥λP\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_Pλ1≥λ2≥...≥λP,对应的特征向量为e⃗1,...,e⃗P\vec{e}_1, \ldots, \vec{e}_Pe 1,...,e P。
可以证明:
- λ1,...,λQ>σn2\lambda_1, \ldots, \lambda_Q > \sigma_n^2λ1,...,λQ>σn2(信号子空间特征值)
- λQ+1=...=λP=σn2\lambda_{Q+1} = \ldots = \lambda_P = \sigma_n^2λQ+1=...=λP=σn2(噪声子空间特征值)
定义噪声子空间:
En=[e⃗Q+1,...,e⃗P]\mathbf{E}n = [\vec{e}{Q+1}, \ldots, \vec{e}_P]En=[e Q+1,...,e P]
C.4 MUSIC伪谱
关键性质:对于真实的信号方向θq\theta_qθq,导向向量b⃗(θq)\vec{b}(\theta_q)b (θq)与噪声子空间正交:
b⃗H(θq)En=0⃗\vec{b}^H(\theta_q)\mathbf{E}_n = \vec{0}b H(θq)En=0
因此,MUSIC伪谱定义为:
PMUSIC(θ)=1b⃗H(θ)EnEnHb⃗(θ)=1∑i=Q+1P∣b⃗H(θ)e⃗i∣2P_{MUSIC}(\theta) = \frac{1}{\vec{b}^H(\theta)\mathbf{E}_n\mathbf{E}n^H\vec{b}(\theta)} = \frac{1}{\sum{i=Q+1}^{P}|\vec{b}^H(\theta)\vec{e}_i|^2}PMUSIC(θ)=b H(θ)EnEnHb (θ)1=∑i=Q+1P∣b H(θ)e i∣21
当θ\thetaθ接近真实信号方向时,分母趋近于零,伪谱产生尖锐峰值。
C.5 分辨率分析
MUSIC算法的角分辨率不受瑞利准则限制,理论上可以达到无限分辨率(仅受噪声和有限样本影响)。这解释了为什么在图15中,仅用4个天线就能分辨相隔5°的两个目标,而传统的傅里叶波束形成方法无法做到这一点。
传统波束形成的角分辨率约为:
Δθ≈λPdcosθ\Delta\theta \approx \frac{\lambda}{Pd\cos\theta}Δθ≈Pdcosθλ
对于P=4P = 4P=4,d=λ/2d = \lambda/2d=λ/2,θ=90°\theta = 90°θ=90°,分辨率约为30°,远大于5°。
MUSIC算法通过利用信号子空间和噪声子空间的正交性,突破了这一限制,实现了超分辨率。