KNN（K近邻算法）-python实现

课堂作业记录

KNN算法简单讲解

复制代码

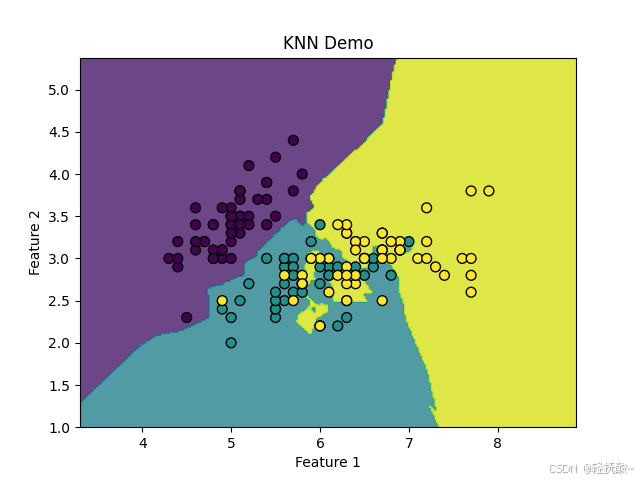
K 近邻算法（K-Nearest Neighbors，简称 KNN）是一种简单且常用的分类和回归算法。

1、knn算法是一种分类算法，将需要分类的元素进行分类，如下图所示，有三种类别，那么一个不知道类别的元素放入其中如何预测其类别？
答：选定一个 k 值，拿出前 k 个距离预测元素最近的元素，哪种类别多就属于哪种。

再问：如果两或者多个种类的数目一样多的呢？
答：计算加权，简单来说就是计算这些有争议的类别内所有元素对预测元素的距离，取距离最小的那个。

再问：如果距离还出现一样的呢？
答：感觉这概率比较小，出现那么就按照代码逻辑随机选一个就行。

代码实现

python 复制代码

from sklearn.datasets import load_iris
import numpy as np
import heapq


# 返回 传入点/预测数据 的预测种类
# --加权--
def beforKKind(data, k, keyNum):
    global iteration
    # 索引0，1，2分别代表索引种类的数量，索引3是最多的种类，有一样多的就
    tempNum, tempWeight = [], np.zeros(keyNum)
    for it, kind in iteration:
        # 欧几里得距离
        length = np.linalg.norm(data - it)
        # 填入堆
        heapq.heappush(tempNum, (length, kind))
    # 处理 tempNum
    result = np.zeros(keyNum + 1)
    for it, kind in heapq.nsmallest(k, tempNum, key=lambda x: x[0]):
        result[kind] += 1
        tempWeight[kind] += it
    # 是否分类无争议
    max_ = max(result)
    if np.sum(result == max_) != 1:
        # 哪几个分类有争议
        maxs = np.where(result == max_)[0]  # 将 [array()] 里的数组(唯一/第一个元素)拿出
        # 计算加权后最佳种类/索引
        print(min(maxs, key=lambda idx: tempWeight[idx]))
        result[keyNum] = min(maxs, key=lambda idx: tempWeight[idx])
    else:
        result[keyNum] = np.argmax(tempWeight)
    # 返回
    return result[keyNum]


# 计算准确率
def calcExactRata():
    global pre_testList, iris_test_kind
    return np.mean(pre_testList == iris_test_kind) * 100


if __name__ == "__main__":
    # ---1、数据处理
    # 获取鸢尾花数据集
    # iris.data [150，4]集合
    # iris.target [0,1,2]三种分类
    iris = load_iris()
    # 数据集种类数量-3
    keyNum = len(set(iris.target))
    # 训练集所占例（分割线）
    Line = 0.8
    iris_data = iris.data
    iris_train, iris_test = np.array_split(iris_data, [int(iris_data.shape[0] * Line)])
    # 训练用迭代元组（数据，种类）
    iteration = list(zip(iris_train, iris.target[0:int(iris_data.shape[0] * Line)]))
    # 测试数据的种类
    iris_test_kind = iris.target[int(iris_data.shape[0] * Line)::]
    
    # ---2、测试数据
    # 定义一个列表记录预测的分类
    K = 5
    pre_testList = []
    for data in iris_test:
        pre_testList.append(beforKKind(data, K, keyNum))
    # 计算准确率
    print(f"准确率：{calcExactRata():.2f}%")


# 准确率记录
# K=3
# 比例    0.5      0.6      0.7      0.8      0.9
# 准确    33.33    16.67    62.22    73.33    100.00
# K=4
# 比例    0.5      0.6      0.7      0.8      0.9
# 准确    33.33    16.67    62.22    76.67    100.00
# K=5
# 比例    0.5      0.6      0.7      0.8      0.9
# 准确    33.33    16.67    62.22    73.33    100.00

（如有不恰当的地方欢迎指正哦 ~o(●'◡'●)o）

参考blogs：

【K 近邻算法】