Python算法实战：从滑动窗口到数学可视化

导入

在编程学习和算法实践中，我们经常会遇到一些经典问题，它们不仅考察我们对数据结构的理解，还考验我们解决问题的思维模式。今天我们将通过四个不同领域的Python实战题目，从字符串处理到数组操作，再到数据可视化，全面展示Python在实际问题中的应用。

题目一：无重复字符的最长子串

给定一个字符串 s ，请找出其中不含有重复字符的最长子串的长度。

代码

python 复制代码

def longest_subString(s):
    char_set = set() # 存放当前窗口内的字符，初始化为空
    left = 0 # 滑动窗口的左边界
    max_len = 0 # 记录最大长度

    for right in range(len(s)): # 右边界遍历字符串s
        while s[right] in char_set: # 若当前字符在窗口中，收缩左边界直到字符移除
            char_set.remove(s[left])
            left += 1
        # 将当前字符添加到窗口中
        char_set.add(s[right])
        # 更新最大长度
        max_len = max(max_len, right - left + 1)
    return max_len

# 测试用例
s = "abcabcbb"
print(longest_subString(s))

代码结果

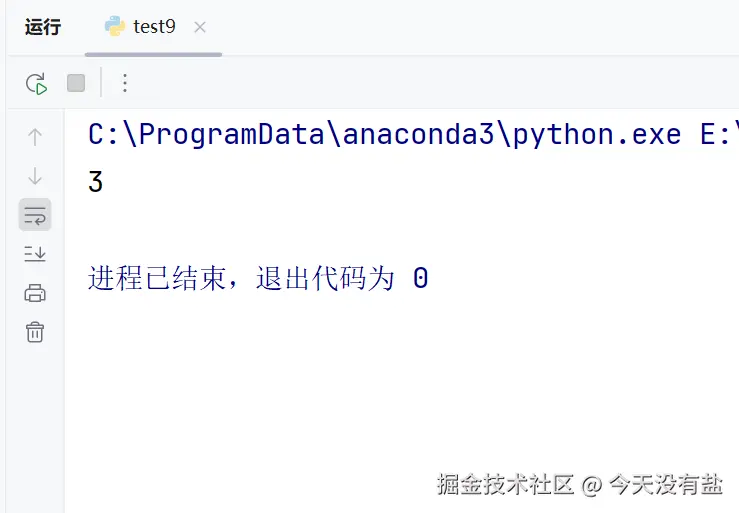
代码分析

滑动窗口算法：使用双指针（left和right）维护一个滑动窗口，保证窗口内字符不重复
集合去重：利用Python的set自动去重特性，快速判断字符是否重复
窗口收缩：当遇到重复字符时，从左边界开始收缩窗口，直到移除重复字符
时间复杂度：O(n)，每个字符最多被访问两次（右指针一次，左指针一次）
空间复杂度：O(min(m,n))，其中m是字符集大小，n是字符串长度

题目二：三数之和

给定一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请返回所有和为 0 且不重复的三元组。

代码

python 复制代码

def three_num(nums):
    res = set() # 存放结果，集合
    n = len(nums)
    for i in range(n): # 第一个元素
        for j in range(i + 1, n): # 第二个元素
            for k in range(j + 1, n): # 第三个元素
                if nums[i] + nums[j] + nums[k] == 0:
                    tmp = tuple(sorted([nums[i], nums[j], nums[k]]))
                    res.add(tmp) # 集合内部自动去重
    return res

nums = [-1,0,1,2,-1,-4]
print(three_num(nums))

代码结果

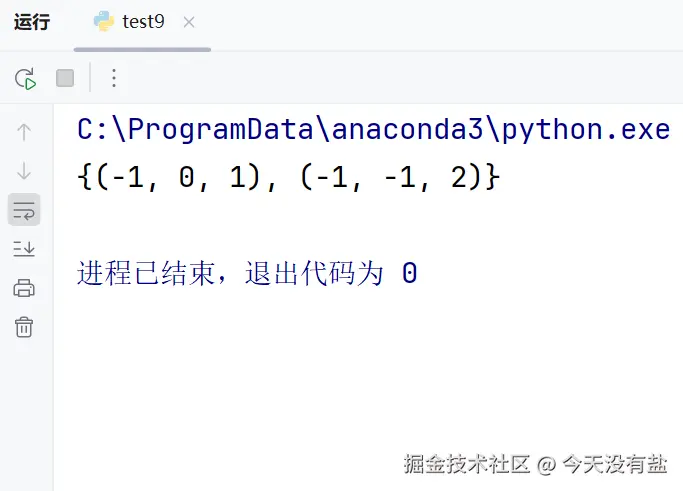
代码分析

暴力枚举：使用三重循环枚举所有可能的三元组组合
自动去重：通过将三元组转换为排序后的元组，利用set自动去重特性
结果存储：使用set存储结果，避免重复三元组的出现
时间复杂度：O(n³)，对于大规模数据效率较低，但代码简单易懂
改进空间：可以使用排序+双指针的方法优化到O(n²)时间复杂度

题目三：最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

代码

python 复制代码

def longest_subNums(nums):
    num_set = set(nums) # 存放数组，作为一个参考基准
    max_len = 0 # 记录最大长度
    for num in num_set:
        if num - 1 not in num_set: # 如果num-1不在集合中
            current_num = num # 记录当前数字
            current_len = 1 # 记录当前长度
            # 往后遍历连续的数字
            while current_num + 1 in num_set:
                current_num += 1
                current_len += 1
            # 更新最大长度
            max_len = max(max_len, current_len)
    return max_len

nums = [100,4,200,1,3,2,200]
print(longest_subNums(nums))

代码结果

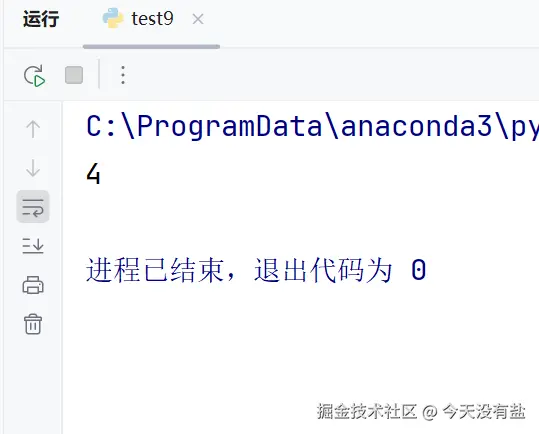
代码分析

集合优化查找：将数组转换为set，实现O(1)时间复杂度的查找
序列起点判断：只有当num-1不在集合中时，才将num作为序列起点，避免重复计算
连续序列扩展：从起点开始向后扩展，统计连续序列的长度
时间复杂度：O(n)，每个数字最多被访问两次（作为起点和作为中间元素）
算法巧妙性：通过判断num-1是否存在，确保每个连续序列只被计算一次

题目四：正弦波和余弦波的可视化

使用 NumPy 和 Matplotlib 绘制一个正弦波和余弦波的图像，要求横坐标为 0 到 2π，每隔 0.1 取一个点，图像中正弦波为蓝色实线，余弦波为红色虚线，并且添加图例、x 轴标签为 'x'，y 轴标签为 'y'，标题为 'sinx and cosx'。

代码

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 2 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)

plt.plot(x, y_sin, 'b-', label="y=sinx")
plt.plot(x, y_cos, "r--", label='y=cosx')
plt.legend()
plt.show()

代码结果

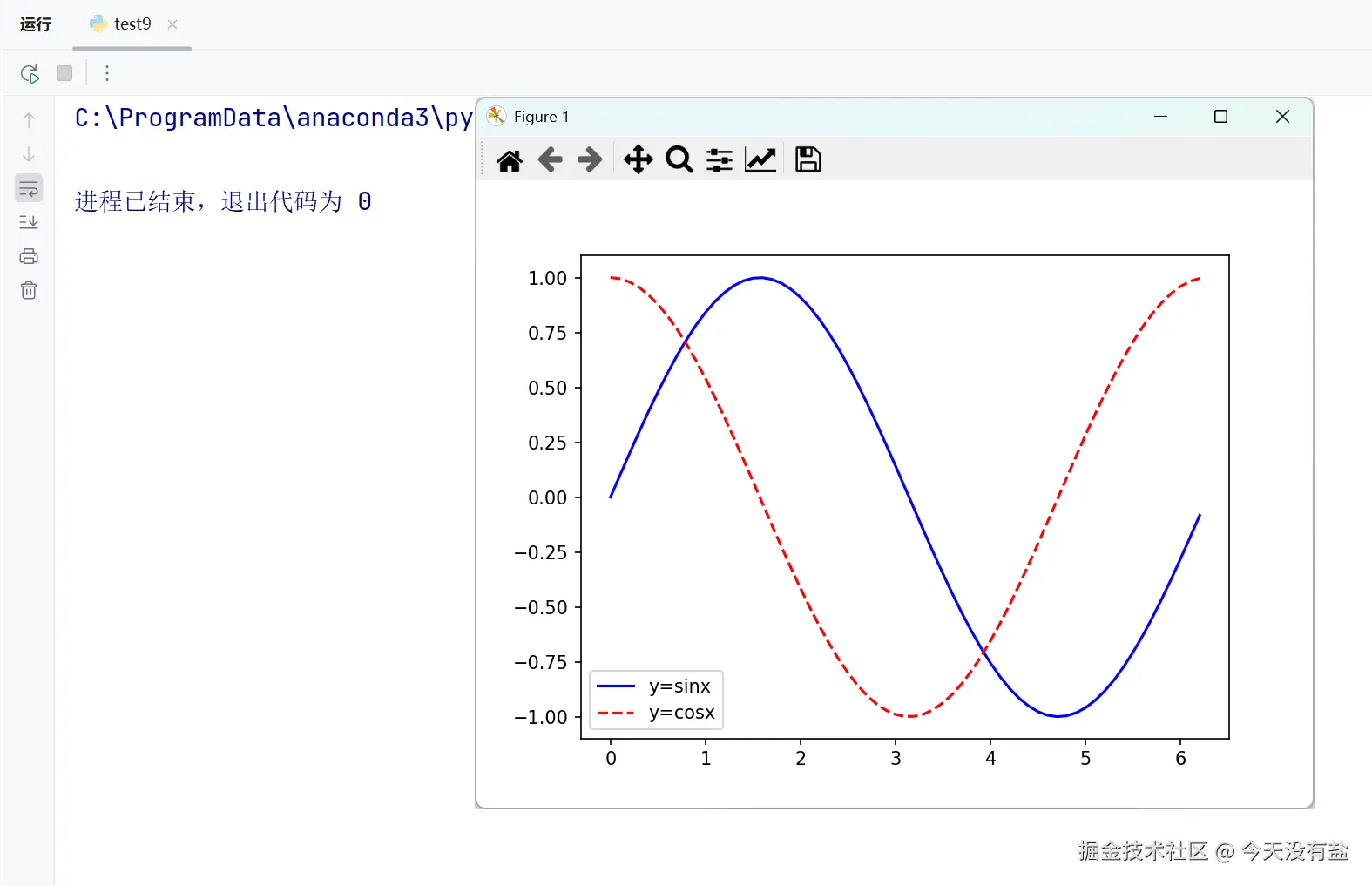
代码分析

数值计算：使用numpy.arange生成等间距的x坐标点，步长为0.1
数学函数：利用numpy的sin和cos函数计算对应的y值
图形绘制 ：
- 正弦波：蓝色实线（'b-'）
- 余弦波：红色虚线（'r--'）
图表美化 ：
- 添加图例说明每条曲线代表的函数
- 自动生成坐标轴标签和标题
可视化效果：清晰展示正弦和余弦函数的周期性特征和相位关系

总结

通过这四个实战题目，我们深入了解了Python在不同场景下的应用：

算法思维提升

滑动窗口：适用于子串、子数组类问题，通过动态维护窗口来优化性能
集合去重：利用数据结构的特性简化代码逻辑，提高效率
数学可视化：将抽象数学概念转化为直观图形，加深理解