算法基础教学第一步：数据结构

有很多小伙伴在后台私信我说对于代码很模糊，看不懂我发的博客代码，一些大模型功能的实现觉得很困难，代码能力的薄弱确实让我们在热爱的领域进步举步维艰，所以我准备出几期基础的算法教学，帮助大家学习。

当然如果你的目标是去大厂工作，这个可能只能做个基础，最重要还是得刷刷力扣，虽然算法在AI时代弱化了很多，但是我们也要有个基本的概念。

如果你的目标和我一样，不是为了工作，单纯对这个方向感兴趣，作为一个爱好，那么这个系列的博客完全足够了。

本博客主要讲解krahets大佬的算法课程。

首先申明，这个课程非常基础，完全面向初学者，已经懂算法的可以不用看！！！

1.数据结构分类：

常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图，它们可以从"逻辑结构"和"物理结构"两个维度进行分类。

A. 逻辑结构 (Logical Structure)

逻辑结构这是指数据之间逻辑上的关系，不管在电脑里具体怎么存，它们看起来是什么样的。

• 线性结构 (Linear): 数据像一条线一样排队。

  • 例子：数组 (Array)、链表 (Linked List)、栈 (Stack)、队列 (Queue)。

• 非线性结构 (Non-linear): 数据之间关系复杂，不是一对一。

  • 树 (Tree): 一对多（像家谱、文件系统）。

  • 图 (Graph): 多对多（像社交网络、地图导航）。

这里引用一张图：

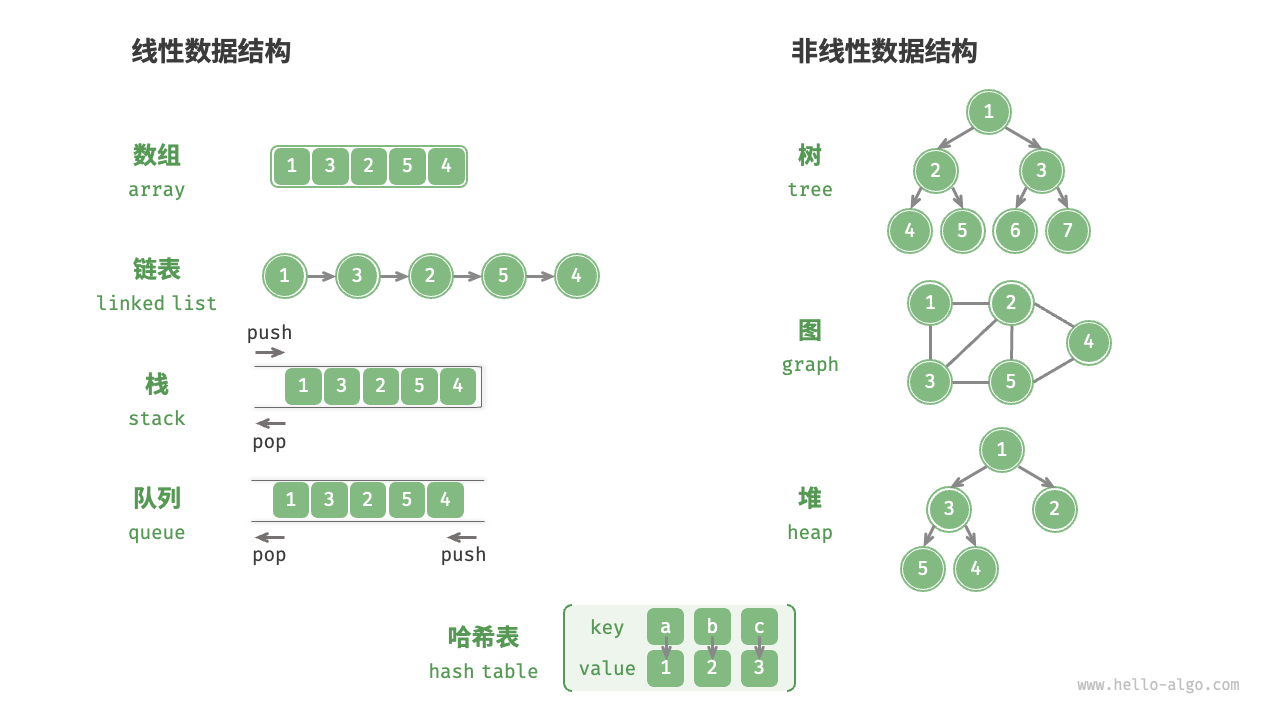
B. 物理结构 (Physical Structure)

这是指数据真正在内存条里是如何存放的。这是决定性能的关键。

• 连续空间 (Contiguous): 数据挤在一起，紧挨着存放。

  • 代表： 数组 (Array)。

  • 优点： 查找快（因为地址连续，可以直接计算偏移量），对 CPU 缓存友好。

  • 缺点： 插入和删除慢（因为要移动后面的所有元素），大小固定（扩容麻烦）。

• 分散空间 (Linked): 数据零散地分布在内存各处，通过"指针"（像线一样）连起来。

  • 代表： 链表 (Linked List)。

  • 优点： 插入删除快（改个指针就行），大小动态灵活。

  • 缺点： 查找慢（必须从头顺藤摸瓜），占用额外空间存指针。

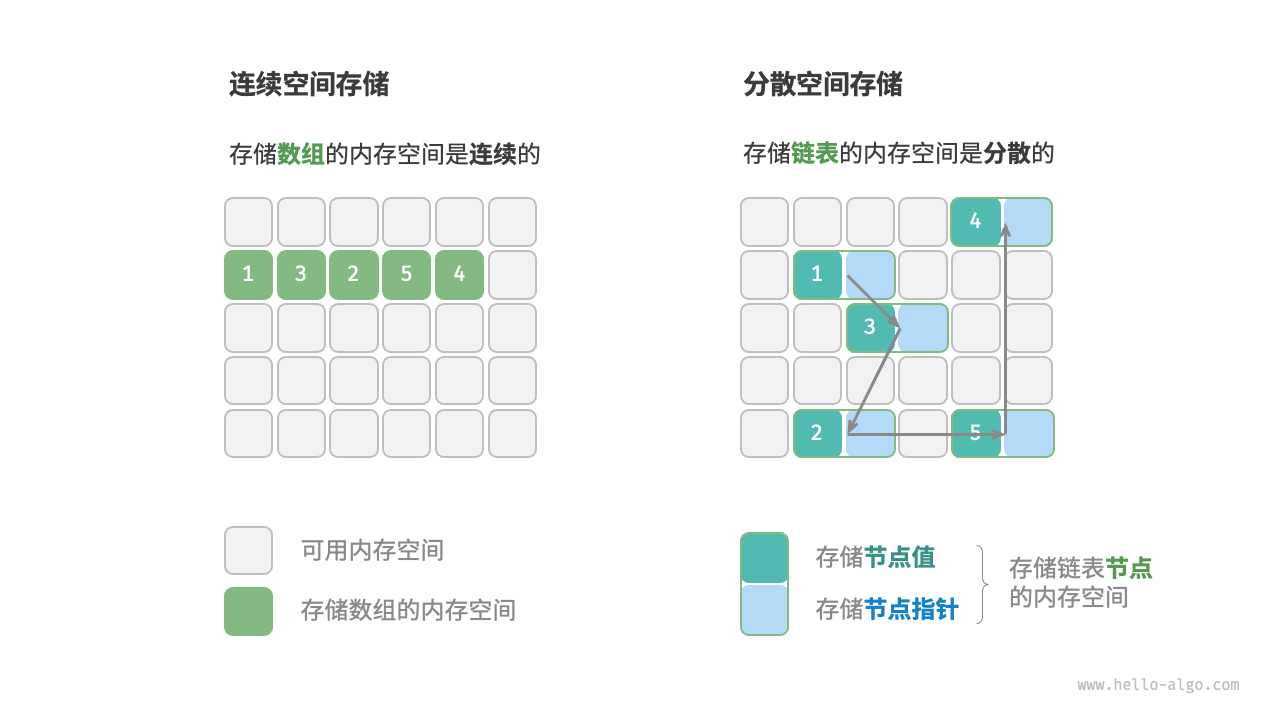
链表在初始化后，仍可以在程序运行过程中对其长度进行调整，因此也称"动态数据结构"。数组在初始化后长度不可变，因此也称"静态数据结构"。值得注意的是，数组可通过重新分配内存实现长度变化，从而具备一定的"动态性"。

有个比较特殊的数据结构，哈希表：

它是数据结构里的"速度之王"。如果说数组是"排队"，哈希表就是"传送门"。

假设你是一个老师，你想找某位同学的试卷。

• 数组/链表模式（遍历）：

  你拿着名字，从第一张卷子开始翻："是张三吗？不是。是李四吗？不是。是王五吗？......找到了。"

  • 耗时： O(n)，人越多越慢。

• 哈希表模式（映射）：

  你有一个神奇的计算器（哈希函数）。你输入名字"王五"，计算器直接显示："在第 8 排第 3 个柜子"。你走过去直接拿，不用翻看其他任何卷子。

  • 耗时： O(1)，无论全校有多少人，你都是一次拿对。

哈希表由三个主要部分组成：

1. Key (键)： 你用来查找的东西（比如 "name": "zhangsan"）。

2. Hash Function (哈希函数)： 这是一个数学公式。它的作用是把任意长度的输入（Key），变成一个固定的数字（索引）。

   • 比如：Hash("zhangsan") = 352

   • 比如：Hash("lisi") = 901

3. Buckets (桶/数组)： 实际存数据的地方。哈希函数算出的数字，就是数据在数组里的下标。

过程演示：

存数据：

你想存 {"apple": 5元}。

1. 哈希函数计算 "apple" 得到索引 02。

2. 把 5元 扔进数组下标为 02 的格子里。

取数据：

你想找 "apple" 多少钱。

1. 哈希函数再次计算 "apple" 得到索引 02。

2. 直接去下标 02 拿数据。不需要遍历！

虽然哈希函数很厉害，但内存是有限的。万一遇到这种情况怎么办？

• Hash("apple") = 02

• Hash("banana") = 02

两个不同的 Key 算出了同一个房间号！这就叫哈希冲突。

怎么解决？

最经典的方法叫拉链法 (Chaining)：

就像如果两个人被分到了同一个单人宿舍，那就把单人床改成"上下铺"（链表）。

• 在下标 02 的位置，不是直接存一个数，而是挂一个链表。

• 里面先存了 apple，后面再挂一个 banana。

• 查找时，先定位到 02，然后顺着链表找一下是 apple 还是 banana。

2.基本数据类型;

当谈及计算机中的数据时，我们会想到文本、图片、视频、语音、3D 模型等各种形式。尽管这些数据的组织形式各异，但它们都由各种基本数据类型构成。

基本数据类型是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种。

第一层面：Python 的 5 大基本数据类型

整数 (Integer, int)

• 也就是： 没有小数点的数字。

• 特点： 在 Python 中，int 是无限精度 的（只要内存够，多大都能存）。不像 C++ 或 Java 有 int / long 之分

浮点数 (Float, float)

• 也就是： 带小数点的数字（科学计数法也算）。

• 特点： Python 的 float 实际上是 C 语言中的 双精度浮点数 (Double, 64-bit)。

布尔值 (Boolean, bool)

• 也就是： 真 (True) 或 假 (False)。其实它在底层就是 1 和 0。

字符串 (String, str)

• 也就是： 文本。

空值 (NoneType, None)

• 也就是： 什么都没有。

第二层面：深度学习必须懂的"底层类型"

只知道 Python 的 int 和 float 是不够的。因为在 PyTorch/TensorFlow 中，为了节省显存（VRAM）和加速计算，我们对数据类型极其敏感。

在 numpy 或 torch.Tensor 中，基本类型被划分得更细：

这是你训练大模型时最关心的。

• float32 (FP32, 单精度): 深度学习的默认标准。

• float16 (FP16, 半精度): 显存占用减半，训练速度翻倍。混合精度训练（Mixed Precision）的核心。

• bfloat16 (BF16): Google 搞出来的，专门为 AI 设计。为了在大模型训练中防止溢出，牺牲了精度，保留了指数位。现在的大模型（如 LLaMA）基本都在用这个。

• float64 (FP64, Double): Python 原生 float 的默认精度。但在深度学习中极少使用，因为太占显存且计算慢。

整数的位数

• int64 (Long): PyTorch 中 Embedding 层查找 Token ID 时，通常要求索引是 int64（或者 LongTensor）。

• int8 (Byte): 量化（Quantization）时会用到。把大模型参数从 float 压成 int8，模型体积直接缩小 4 倍，甚至可以在手机上跑。

基本数据类型以二进制的形式存储在计算机中。一个二进制位即为 1比特。在绝大多数现代操作系统中， 1字节（byte）由 8比特（bit）组成。

基本数据类型的取值范围取决于其占用的空间大小。

类型 (Type)	占用空间	取值范围	典型应用场景
int8	1 Byte	-128 ~ 127	模型量化 (Quantization)
uint8	1 Byte	0 ~ 255	图像像素 (RGB 值)
int16	2 Bytes	-32,768 ~ 32,767	音频处理
int32	4 Bytes	约 -21亿 ~ 21亿	某些索引
int64 (Long)	8 Bytes	极大 (约 \\pm 9 \\times 10\^{18})	PyTorch 默认索引类型

类型 (Type)	占用空间	取值范围 (Approx)	精度 (有效位数)	典型应用场景
float16 (FP16)	2 Bytes		~3-4 位	混合精度训练
bfloat16	2 Bytes		~2-3 位	大模型 (LLaMA等)
float32 (FP32)	4 Bytes		~7 位	深度学习标准精度
float64 (Double)	8 Bytes		~15-17 位	科学计算 (非AI)

那么，基本数据类型与数据结构之间有什么联系呢？我们知道，数据结构是在计算机中组织与存储数据的方式。这句话的主语是"结构"而非"数据"。

如果想表示"一排数字"，我们自然会想到使用数组。这是因为数组的线性结构可以表示数字的相邻关系和顺序关系，但至于存储的内容是整数 int、小数 float 还是字符 char ，则与"数据结构"无关。

换句话说，基本数据类型提供了数据的"内容类型"，而数据结构提供了数据的"组织方式"。

3.数字编码

在上一节的表格中我们发现，所有整数类型能够表示的负数都比正数多一个，例如 int8的取值范围是 -128 ~ 127 。这个现象比较反直觉，它的内在原因涉及原码、反码、补码的相关知识。

在计算机眼里，没有数字，只有开关（0 和 1） 。 所谓的"数字编码"，就是如何制定一套规则，把现实世界的数学（整数、小数、负数）翻译成 0 和 1 的排列组合。

主要分为两大块：整数编码（补码系统） 和 浮点数编码（IEEE 754标准）。

这个就是一个扩展阅读，不上王者不用学，甚至我认为作为教材这个都有点多余了，只要知道这个大概的概念就行了

第一部分：整数编码 (Integer)

1. 正整数：原码 (Sign-Magnitude)

这是最符合人类直觉的。

• 假设我们需要 4 位二进制（4-bit）。

• 数字 5 对应0101

• 数字 2 对应 0010

• 很简单，直接转二进制。

2. 负数的难题

如果要表示 负数（如 -5），怎么办？

• 直觉想法（原码）： 用第一位（最高位）当符号位。0 是正，1 是负。

  • +5 = 0101

  • -5 = 1101

• 这就出大问题了：

  1. 两个零： 会出现 0000 (+0) 和 1000 (-0)。这就浪费了一个编码，而且逻辑判断麻烦。

  2. 数学运算无法统一： 计算机希望只设计"加法器"，不设计"减法器"（为了省电路）。

     • 如果用原码算 1 + (-1)：

     • 0001 + 1001 = 1010 (-2)。结果错了！

3. 完美的解决方案：补码 (Two's Complement)

现代计算机（包括 Python 底层、PyTorch 的 int）全都使用补码。

规则：

• 正数： 保持不变。

• 负数： 取反（0变1，1变0），然后加 1。

为什么这样设计？（核心原理：时钟理论）

想象一个只有 12 小时的时钟。

• 现在的指针是 2 点。

• 你想让指针倒退 1 小时（做减法：）。

• 方法一： 逆时针拨 1 格 1 点。

• 方法二： 顺时针拨 11 格 也是 1 点

补码就是那个"顺时针拨 11 格"。 它把"减法"变成了"加法"（加上一个很大的数，利用溢出回到正确位置）。

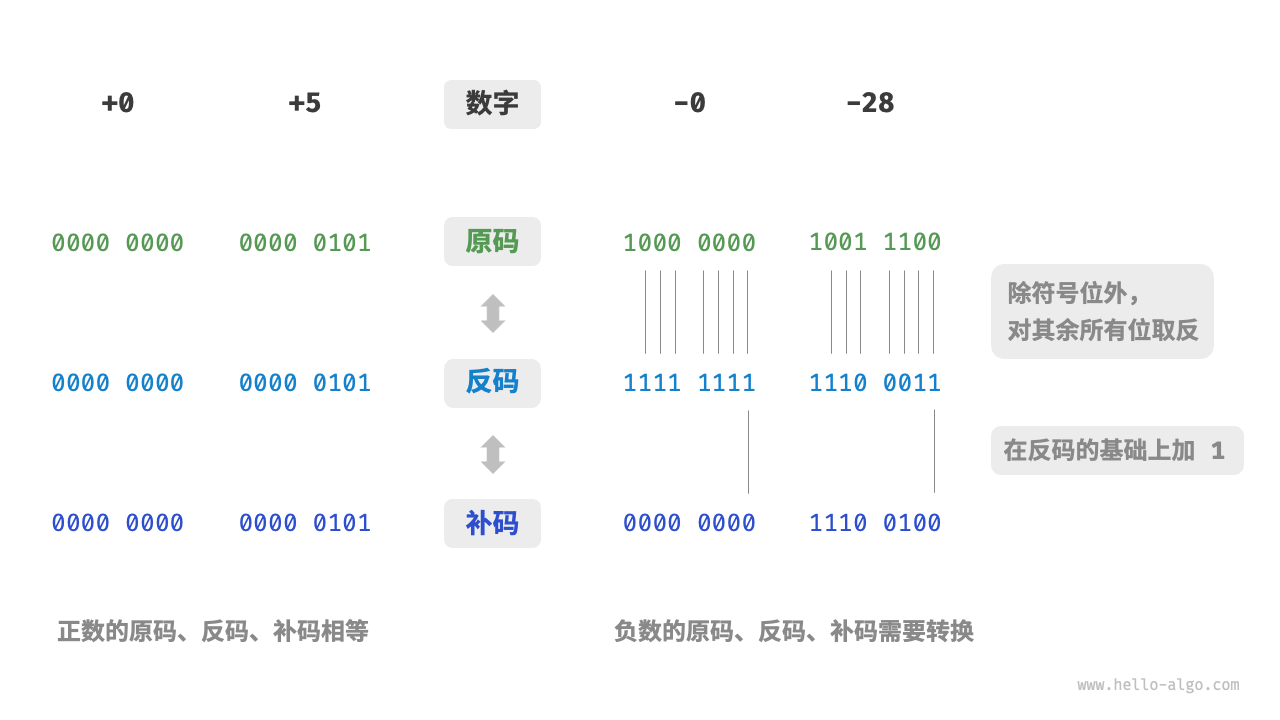
例子：计算 1 + (-1) (4-bit 系统)

1. +1 的补码 0001

2. -1 的补码原码 1001 反码 1110 加1 1111

3. 相加：

   

4. 因为只有 4 位，最高位的 1 溢出丢弃，结果变成 0000 (即 0)。结果正确！

启示： 这就是为什么 int8 的范围是 -128 到 127。因为 10000000 被规定为 -128，而没有对应的正数 +128。

第二部分：浮点数编码 (Float - IEEE 754)

计算机存小数，用的是 "科学计数法" 的二进制版。

公式：

它把 32 个比特位（以 float32 为例）切成了三段：

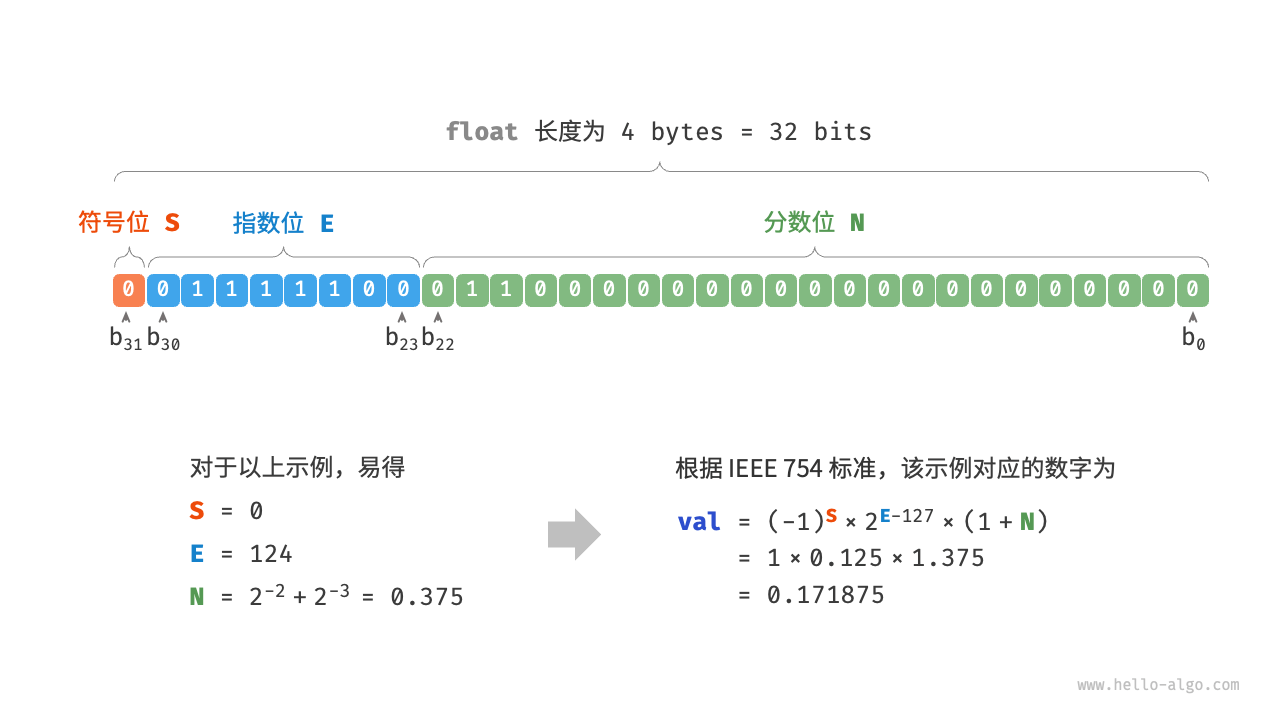
1. 符号位 (Sign, S) - 1 bit

• 0 代表正，1 代表负。

2. 指数位 (Exponent, E) - 8 bits

• 决定了数字的 大小范围（Range）。

• 相当于科学计数法 里的那个 5。

• 指数位越多，能表示的数就越大（比如能到 还是 ）。

3. 尾数位 (Mantissa / Fraction, M) - 23 bits

• 决定了数字的 精度（Precision）。

• 相当于科学计数法 1.23456...里的 23456。

• 尾数位越多，小数点后面的数字越精确。

为了彻底理解"编码只是解释方式"，请看下面这串 32 位的二进制：

0011 1111 1000 0000 0000 0000 0000 0000

• 如果你告诉 CPU "这是个整数 (int32)" ： CPU 会按补码读，结果是 1,065,353,216。

• 如果你告诉 CPU "这是个浮点数 (float32)" ： CPU 会按 IEEE 754 读（符号0，指数127，尾数0），结果是 1.0。

结论：数据结构定义了内存的布局，而数据类型（编码）定义了如何理解这块内存。

4.字符编码

这个就太熟悉了，我们深度学习基本都会，但是我还是讲一下吧，毕竟有很多交叉学科的同学可能没有接触过

在计算机中，所有数据都是以二进制数的形式存储的，字符 char 也不例外。为了表示字符，我们需要建立一套"字符集"，规定每个字符和二进制数之间的一一对应关系。有了字符集之后，计算机就可以通过查表完成二进制数到字符的转换。

++ASCII 码++是最早出现的字符集，其全称为 American Standard Code for Information Interchange（美国标准信息交换代码）。它使用 7 位二进制数（一个字节的低 7 位）表示一个字符，最多能够表示 128 个不同的字符。如图 3-6 所示，ASCII 码包括英文字母的大小写、数字 0 ~ 9、一些标点符号，以及一些控制字符（如换行符和制表符）。

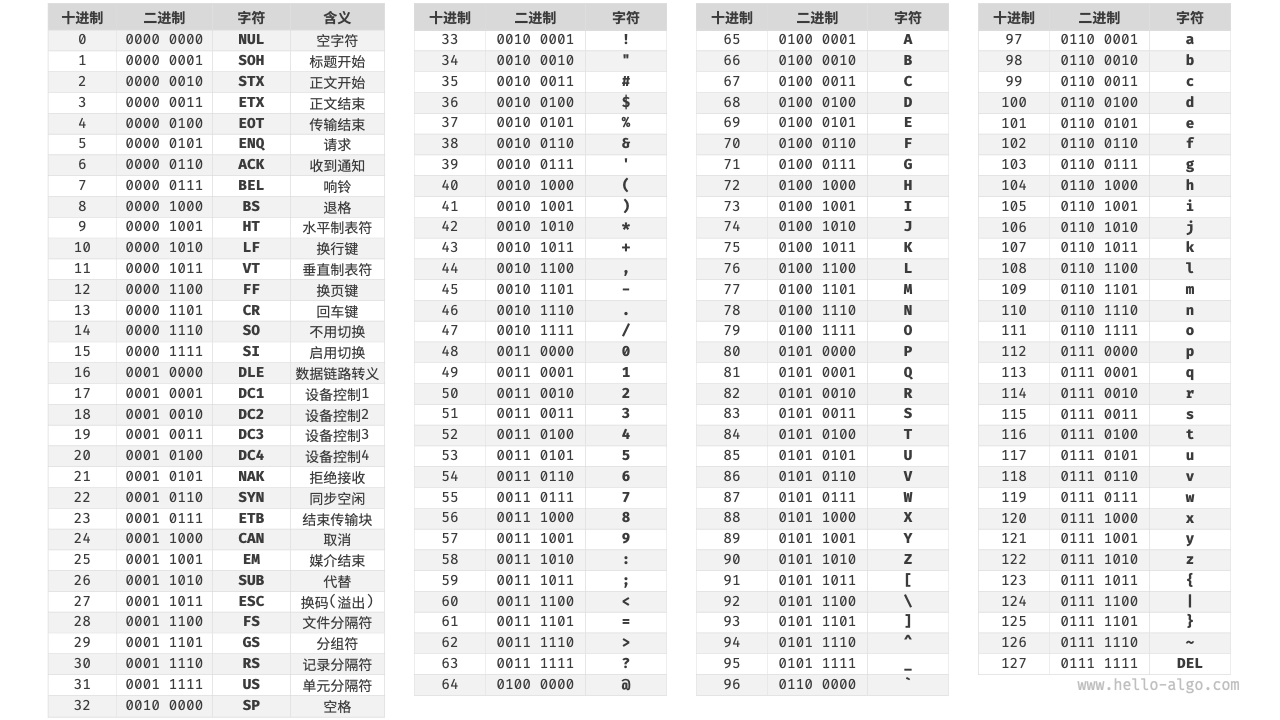
然而，ASCII 码仅能够表示英文 。随着计算机的全球化，诞生了一种能够表示更多语言的 ++EASCII++ 字符集。它在 ASCII 的 7 位基础上扩展到 8 位，能够表示 256 个不同的字符。

在世界范围内，陆续出现了一批适用于不同地区的 EASCII 字符集。这些字符集的前 128 个字符统一为 ASCII 码，后 128 个字符定义不同，以适应不同语言的需求。

后来人们发现，EASCII 码仍然无法满足许多语言的字符数量要求 。比如汉字有近十万个，光日常使用的就有几千个。中国国家标准总局于 1980 年发布了 ++GB2312++ 字符集，其收录了 6763 个汉字，基本满足了汉字的计算机处理需要。

然而，GB2312 无法处理部分罕见字和繁体字。++GBK++ 字符集是在 GB2312 的基础上扩展得到的，它共收录了 21886 个汉字。在 GBK 的编码方案中，ASCII 字符使用一个字节表示，汉字使用两个字节表示。

Unicode 字符集

如果推出一个足够完整的字符集，将世界范围内的所有语言和符号都收录其中，不就可以解决跨语言环境和乱码问题了吗？在这种想法的驱动下，一个大而全的字符集 Unicode 应运而生。

++Unicode++ 的中文名称为"统一码"，理论上能容纳 100 多万个字符。它致力于将全球范围内的字符纳入统一的字符集之中，提供一种通用的字符集来处理和显示各种语言文字，减少因为编码标准不同而产生的乱码问题。

自 1991 年发布以来，Unicode 不断扩充新的语言与字符。截至 2022 年 9 月，Unicode 已经包含 149186 个字符，包括各种语言的字符、符号甚至表情符号等。在庞大的 Unicode 字符集中，常用的字符占用 2 字节，有些生僻的字符占用 3 字节甚至 4 字节。

Unicode 是一种通用字符集，本质上是给每个字符分配一个编号（称为"码点"），但它并没有规定在计算机中如何存储这些字符码点。我们不禁会问：当多种长度的 Unicode 码点同时出现在一个文本中时，系统如何解析字符？例如给定一个长度为 2 字节的编码，系统如何确认它是一个 2 字节的字符还是两个 1 字节的字符？

对于以上问题，一种直接的解决方案是将所有字符存储为等长的编码。如图 3-7 所示，"Hello"中的每个字符占用 1 字节，"算法"中的每个字符占用 2 字节。我们可以通过高位填 0 将"Hello 算法"中的所有字符都编码为 2 字节长度。这样系统就可以每隔 2 字节解析一个字符，恢复这个短语的内容了。

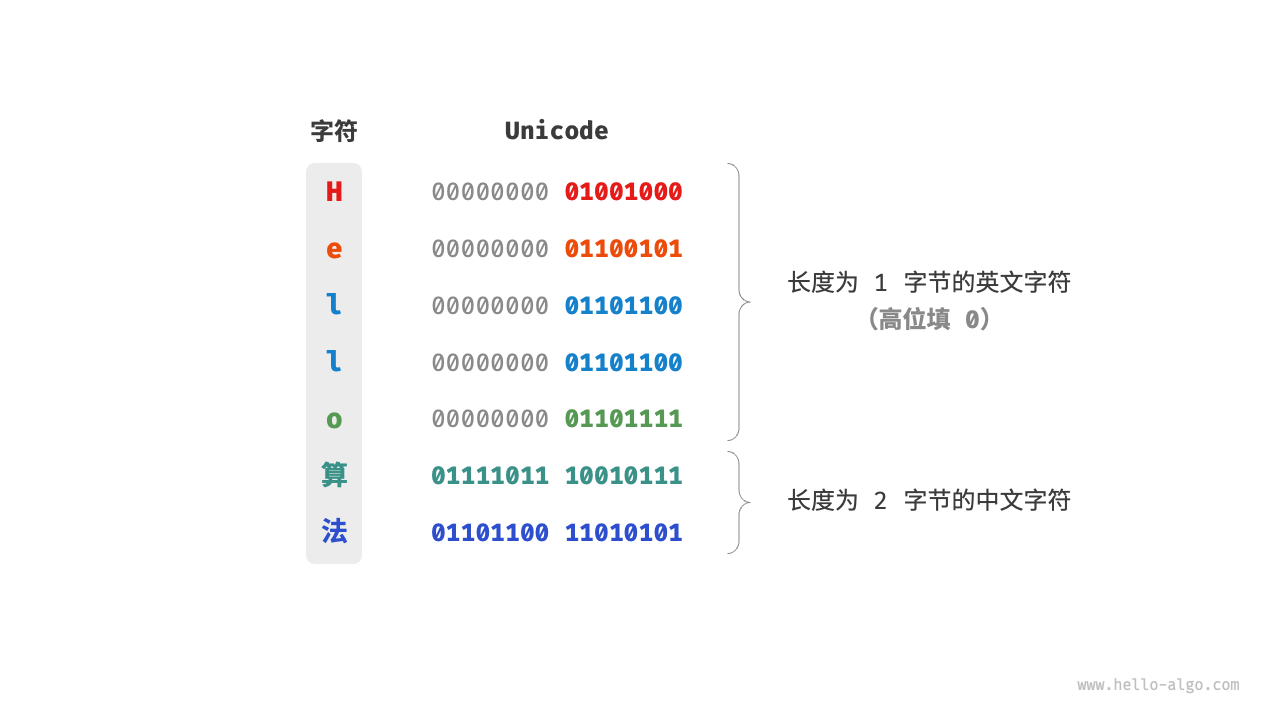
然而 ASCII 码已经向我们证明，编码英文只需 1 字节。若采用上述方案，英文文本占用空间的大小将会是 ASCII 编码下的两倍，非常浪费内存空间。因此，我们需要一种更加高效的 Unicode 编码方法。

UTF-8 编码

目前，UTF-8 已成为国际上使用最广泛的 Unicode 编码方法。它是一种可变长度的编码，使用 1 到 4 字节来表示一个字符，根据字符的复杂性而变。ASCII 字符只需 1 字节，拉丁字母和希腊字母需要 2 字节，常用的中文字符需要 3 字节，其他的一些生僻字符需要 4 字节。

以上讨论的都是字符串在编程语言中的存储方式，这和字符串如何在文件中存储或在网络中传输是不同的问题。在文件存储或网络传输中，我们通常会将字符串编码为 UTF-8 格式，以达到最优的兼容性和空间效率。