【技术深度】【安全】Remote Password Protection:一套密码永不上传的登录协议方案(含盲签 + Pairing + Crypto 模块)
作者:ZFJ_张福杰
博客:https://zfj1128.blog.csdn.net
日期:2025-11-30
关键词:密码学、盲签、双线性映射、远程密码保护、HSM、零信任
前言
传统密码验证机制(如 Django / PHP / Java Web)高度依赖:
- 服务端保存 password hash
- 登录时上传密码 hash 或明文
结果导致:
- 服务端数据库一旦泄露 → 攻击者可离线暴力破解
- 用户弱密码更是瞬间被撞库
- 密码无脱敏风险极高
有没有办法做到:
服务端永远不知道用户密码,甚至不知道密码哈希?
数据库泄露也无法用于暴力破解密码?
答案是:可以的。
这里我将给出一套基于盲化(Blind) + Pairing(双线性映射) + 主密钥混合 的 Remote Password Protection 技术方案。
架构图
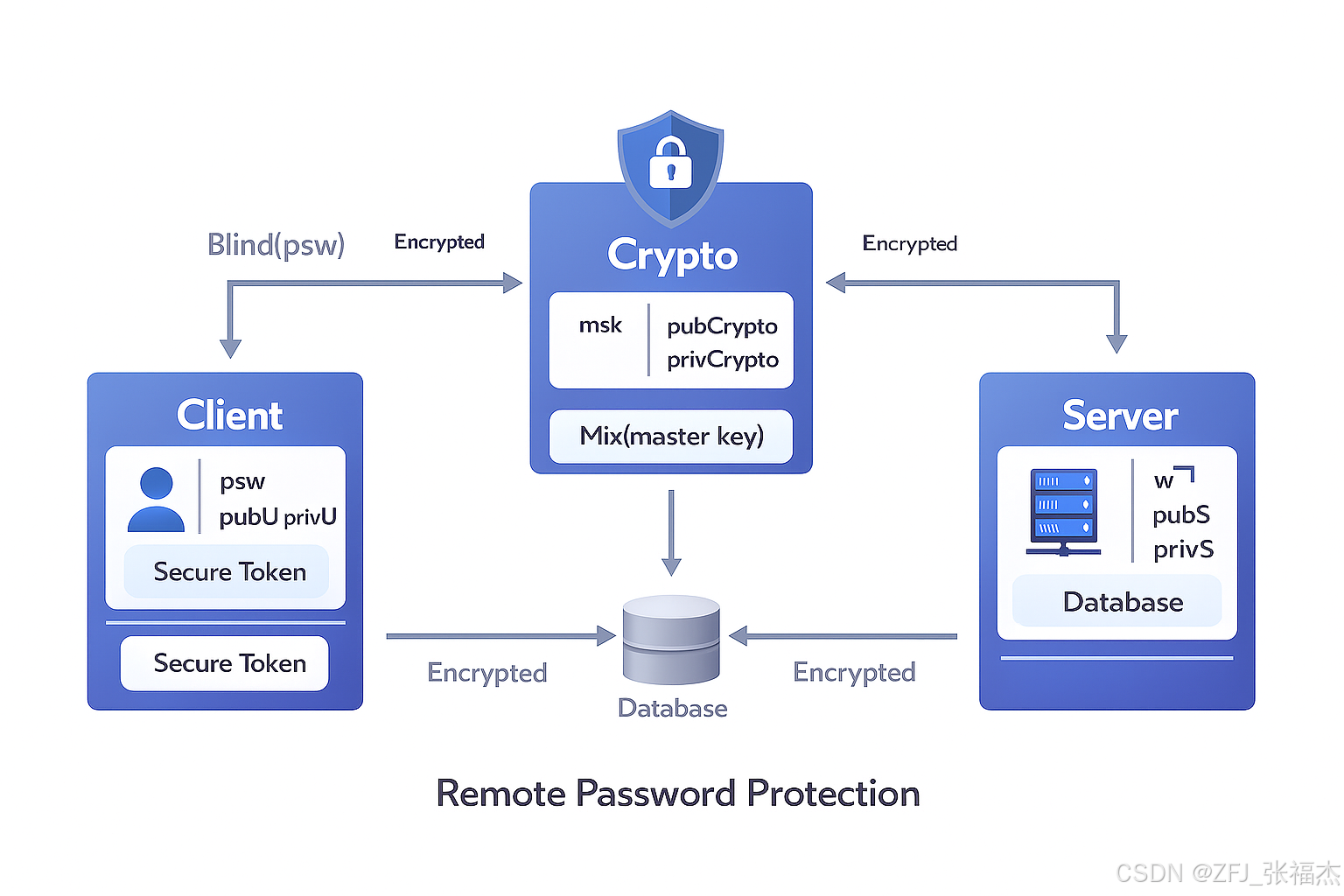
💀💀💀在交易所中,任何安全小漏洞都可以是灾难性的。💀💀💀
一、协议参与方
系统由三个角色组成:
| 角色 | 说明 |
|---|---|
| Client | 用户设备(浏览器 / App) |
| Server | 业务服务器 |
| Crypto | 密码服务,持有主密钥 msk(通常运行在硬件安全模块 HSM 或可信执行环境 TEE) |
为什么要有 Crypto?
答:因为只有它持有主密钥 msk,如果 Server 泄露也无法暴力破解密码。
二、核心思想
协议基于三件事:
2.1 密码盲化(Blind)
客户端对密码 H(psw) 进行随机盲化:
x = H ( p s w ) r x = H(psw)^r x=H(psw)r
服务器完全无法看到 H(psw)。
2.2 双线性映射 Pairing
服务器用自己的秘密 w 参与运算:
v = H ( u i d ∣ ∣ w ) y 1 = e ( v , x ) v = H(uid || w) y1 = e(v, x) v=H(uid∣∣w)y1=e(v,x)
e() 是双线性映射,允许双方秘密混合,但没人能反推。
2.3 主密钥混合(Crypto)
Crypto 再加入 msk 混合:
k = H ( w ∣ ∣ m s k ) y = y 1 k k = H(w || msk) y = y1^k k=H(w∣∣msk)y=y1k
这让最终结果 z 同时绑定:
- 用户密码
- 服务器秘密 w
- Crypto 的主密钥 msk
任何一方单独泄露都无法破解密码。
三、方案对比解析
下面分别介绍三种方案。
3.1 方案1:基础注册 + 登录流程
适用于所有需要高安全登录的场景。
3.1.1 流程:
- Client:盲化密码 → x
- Server:生成 uid、计算 v
- Server:计算 y1 = e(v, x)
- Crypto:混合主密钥得到 y
- Client:去盲化 y → z(最终凭证)
后续登录时再计算一遍,若 z 相同则登录成功。
3.1.2 安全性
- 服务端永远不知道密码,也不知道密码哈希
- 数据库泄露无法暴力破解
- 客户端永远不上传密码
3.1.3 方案图

3.2 方案2:增强版(加入 Token + 安全通道)
3.2.1 流程:
在 方案1 基础上增加:
- ✔ Client ↔ Server 会话密钥
- ✔ Client ↔ Crypto 会话密钥
- ✔ Crypto 使用私钥签 token(用户登录凭证)
3.2.2 提升:
- 前后端可以安全通信
- Token 可用于后续接口鉴权
- 加密通道确保传输安全
3.2.3 适合:
- Web 登录
- 多节点 API 系统
- 单点登录(SSO)
3.2.4 方案图

3.3 方案3:旧系统升级方案(兼容 MD5)
非常贴合真实企业场景。
3.3.1 场景:
- 旧系统保存
md5(psw) - 新系统需要盲签协议
3.3.2 方案:
- 用户输入密码
- Server 用旧规则验证
H(salt, md5(psw)) - 验证通过 → 迁移到新协议
- Server 生成 pubU / privU
- 完成盲签注册流程
3.3.3 最终实现:
- ✔ 新旧系统平滑迁移
- ✔ 不需要用户重设密码
- ✔ 用户透明升级
3.3.4 方案图

四、总结
Remote Password Protection 是一套具有高安全性、低信任依赖、可升级性的认证协议。
它具备:
- 密码永不上传
- 服务端无可逆哈希
- 数据库泄露不可暴力破解
- 支持 Token 与安全通道
- 支持旧系统无缝升级
适用于:
- 交易所
- 银行
- 高安全 SaaS
- 企业级身份认证系统
未来的安全密码体系,一定是这种"密码永不上传"的方向。
五、完整数学公式(带推导说明)
以下为可直接渲染的 LaTeX:
5.1 密码盲化(Blind)
l a t e x x = blind ( p s w ) = H ( p s w ) r latexx = \text{blind}(psw) = H(psw)^r latexx=blind(psw)=H(psw)r
5.2 服务器秘密生成
l a t e x v = H ( u i d ∥ w ) latexv = H(uid \parallel w) latexv=H(uid∥w)
5.3 双线性映射计算
l a t e x y 1 = e ( v , x ) latexy_1 = e(v, x) latexy1=e(v,x)
5.4 Crypto 主密钥混合
l a t e x k = H ( w ∥ m s k ) latexk = H(w \parallel msk) latexk=H(w∥msk)
l a t e x y = y 1 k latexy = y_1^k latexy=y1k
5.5 客户端去盲化
l a t e x z = unblind ( y ) latexz = \text{unblind}(y) latexz=unblind(y)
最终凭证 z:
l a t e x z = e ( v , H ( p s w ) ) k latexz = e(v, H(psw))^k latexz=e(v,H(psw))k
5.6 登录验证
登录时重新计算:
l a t e x z ′ = e ( H ( u i d ∥ w ) , H ( p s w ) ) H ( w ∥ m s k ) latexz' = e(H(uid \parallel w), H(psw))^{H(w \parallel msk)} latexz′=e(H(uid∥w),H(psw))H(w∥msk)
验证:
l a t e x LoginSuccess ⟺ z ′ = z latex \text{LoginSuccess} \iff z' = z latexLoginSuccess⟺z′=z
关于作者(ZFJ_张福杰)
- 官网:https://zfjsafe.com
- 博客:https://zfj1128.blog.csdn.net
- Github:https://github.com/zfjsyqk
- Gitee:https://gitee.com/zfj1128
- 打赏:https://zfjsafe.com/paycode