用 AI 做了几个超炫酷的 Flutter 动画，同时又差点被 AI 气死

AI 时代之后，对于开发者来说最缺乏的其实是想象力，而随着 AI 成熟之后，很多以前需要"费劲巴拉"才能实现的效果，现在只需要几句话搭配对应的资料就可以复刻，特别是在数学公式到 UI 的转换实现上。

而本次介绍的几种动画效果，没用任何 OpenGL 相关实现，都是纯 Dart 代码完成，整体流畅程度还过得去，都是基于已有的数学公式和资料复刻到 Flutter 的效果：

奇异粒子动画（Strange Attractors）	斐波那契球体动画（Fibonacci Sphere）	星云动画（Galaxy Scene）

奇异粒子动画

首先是奇异粒子动画，这是一个非常酷的视觉场景，概念是它们一般被被称为奇异吸引子 (Strange Attractors)，它们是混沌理论中的经典模型，而当我看到它们还搭配了公式时，我就知道 AI 的价值来了。

要在一个 Flutter 页面中实现这四种粒子的 3D 运动轨迹渲染，需要解决以下几个关键点：

• 数学模型：将图片中的微分方程转化为代码（欧拉积分法更新粒子位置）

• 3D 到 2D 的投影：Flutter 的 Canvas 是 2D 的，所以需要一个简单的投影算法将 (x, y, z) 坐标转换为屏幕上的 (u, v) 坐标，最好加上一点旋转让 3D 感更强

然后再基于数学公式，就可以直观的呈现数学的美丽一面。

核心公式实现

这这个实现中，核心就是模拟物理运动规律，所以 AI 实现了一个 _updatePhysics 方法，在方法里使用欧拉积分法 (Euler Integration) 将微分方程转化为代码，即：

新位置 = 旧位置 + 变化率(dx, dy, dz) * 时间步长(dt)。

具体到每个动画效果就是：

A. Halvorsen Attractor

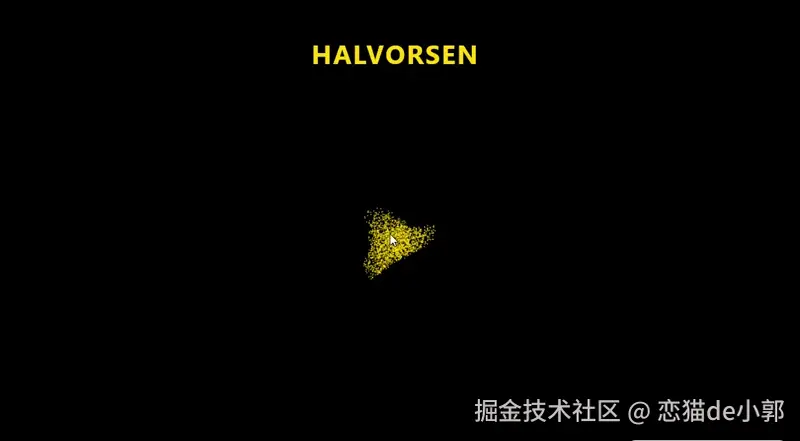
Halvorsen 是一个具有循环对称性的混沌系统，对应公式代码实现公式为:

const a = 1.4;
dx = -a * p.x - 4 * p.y - 4 * p.z - (p.y * p.y);
dy = -a * p.y - 4 * p.z - 4 * p.x - (p.z * p.z);
dz = -a * p.z - 4 * p.x - 4 * p.y - (p.x * p.x);

B. Lorenz Attractor

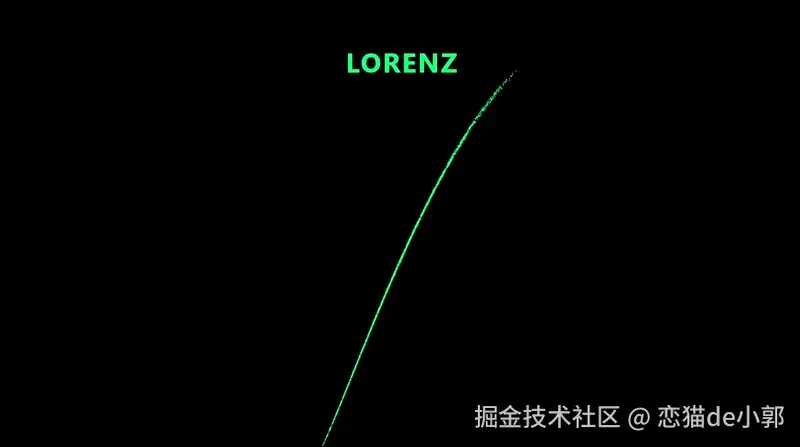
这是经典的混沌模型，呈现"蝴蝶效应"形状，对应公式的代码实现:、

dx = sigma * (p.y - p.x);
dy = p.x * (rho - p.z) - p.y;
dz = p.x * p.y - beta * p.z;

C. Aizawa Attractor

其实从结构上看，这个实现会更复杂，因为中间有一个明显的管状结构，需要复杂的缩放和位移，对应公式的代码实现:

dx = (p.z - b) * p.x - d * p.y;
dy = d * p.x + (p.z - b) * p.y;
dz = c + a * p.z - (p.z * p.z * p.z) / 3 - (p.x * p.x + p.y * p.y) * (1 + e * p.z) + f * p.z * (p.x * p.x * p.x);

D. Sprott B Attractor

这个公式主要呈现出类似环状或星系的结构，对应的代码实现为

dx = a * p.y * p.z;
dy = p.x - p.y;
dz = b - p.x * p.y;

结论

而在实际上，这些公式为什么能产生这些奇异的图形，简单来说就是需要从**"微分方程" (Differential Equations)** 的本质看起，其实在代码中，我们看到的公式计算的并不是粒子的"位置"，而是粒子的"速度"（或者说是趋势）：

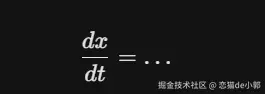
意思就是："在这一瞬间，x 坐标应该变化多少？ "，当我们把 x, y, z 三个维度的变化率组合在一起，就形成了一个**"向量场" (Vector Field)，你可以把整个空间想象成一条充满暗流的河流，而这些公式就是告诉水流在每一个具体的点上应该往哪个方向流，流多快**。

举个例子， Halvorsen Attractor 的视觉效果是粒子在三个对称的圆环之间穿梭，像一个纠缠在一起的三叶结，对应的公式逻辑大致为：

Halvorsen 的公式是循环对称的，因为 x 的变化取决于 y ， y 取决于 z ， z 又取决于 x ，这种"你推我，我推他，他推你"的结构，导致粒子无法在一个平面停留，必须在三个维度间不断轮转。

而减去 y^2 ，可以让线性部分的 ax-4y-4z 粒子产生旋转，这里的非线性部分 y^2 就是"折叠力"，粒子跑远时，平方项会迅速变大，产生一股巨大的力量把粒子原本的轨道"掰弯"。

而为什么用 Halvorsen 做例子呢？因为 AI 在做出来第一版的时候，在运行 Halvorsen 效果时，粒子运动一段时间后，屏幕变空，所有粒子消失。

而对应的根本原因是数值发散 (Numerical Divergence)，具体原因有：

1. 数学不稳定性：Halvorsen 方程包含平方项 (y^2, z^2, x^2)，当粒子距离中心稍远时，平方项会让数值瞬间变得极大
2. 积分误差 ：公式使用的是简单的离散算法（每帧加一次 dx * dt），一旦某个粒子因为计算误差稍微偏离轨道，平方项会迅速放大这个误差，导致坐标值在几帧内变成 Infinity（无穷大）或 NaN（非数字），从而出现绘制错误

而 AI 最终通过"检测 + 重置"的机制解决了这个问题：

• 设置电子围栏 (Boundary Check)：

在每一帧计算前，检查粒子的坐标是否超过安全范围（代码中设定为 50）或是否变成 NaN

if (p.x.abs() > 50 || ... || p.x.isNaN) { ... }

• 自动重生机制 (Respawn)：

一旦检测到粒子"逃逸"或"计算崩溃"，立即调用 _resetSingleParticle(p) 之类的方法将它重置回原点附近的随机位置，这不仅修复了 BUG，还让粒子看起来像源源不断地从中心喷涌而出。

• 微调步长 (Step Size)，

针对 Halvorsen，将时间步长 dt 从默认的 0.01 降低到了 0.004，步长越小计算越精确，发生"逃逸"的概率也就越低。

最后

其实可以看到 Flutter 复刻出现的效果和原图还是有点差别，其中最核心之一还是粒子的数量和计算的精细度，不过可以看出来，已经是非常不错的效果了。

斐波那契球体（Fibonacci Sphere）

斐波那契球体的特点是点在球面上分布极其均匀，普通的方法（如经纬度划分）会在球的两极产生点的密集堆积，而斐波那契球体算法能让点在球面上极度均匀地分布，每个点占据的面积几乎相等。

而针对这个效果，需要解决的点在于：

• 数学算法：如何根据斐波那契螺旋算法在 3D 球面上生成点

• 渲染与投影：如何将 3D 坐标投影到 2D 屏幕，并处理透视关系（近大远小）

所以 AI 首先需要的是实现一个球体算法，核心思想是将原本在 2D 平面上画向日葵种子的"黄金螺旋"算法，投影到了 3D 球面上，具体是利用黄金角 (Golden Angle) 来决定每个点的角度偏移：

对应的代码实现为：

final double goldenAngle = pi * (3 - sqrt(5)); // 约 137.5 度
for (int i = 0; i < numPoints; i++) {
  double y = 1 - (i / (numPoints - 1)) * 2; // y 轴均匀分布
  double radiusAtY = sqrt(1 - y * y);       // 球体公式 x^2 + z^2 = r^2
  double theta = goldenAngle * i;           // 黄金角递增

  double x = cos(theta) * radiusAtY;
  double z = sin(theta) * radiusAtY;
  // ...
}

之后就是 3D 旋转 (Rotation Matrix)，因为生成的点是静止的，为了让球转动，还需要应用旋转矩阵，这里使用了简化的欧拉角旋转（绕 Y 轴自转，绕 X 轴倾斜）：

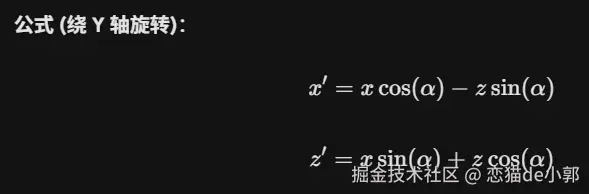
对应的代码为：

// rotationY 是随时间变化的量
double x1 = x * cos(rotationY) - z * sin(rotationY);
double z1 = x * sin(rotationY) + z * cos(rotationY);

然后就是透视投影 (Perspective Projection)，这是让 2D 屏幕产生 3D 纵深感的关键，物体离相机越远（Z 越小/负值），在屏幕上看起来就越小，位置越靠近中心：

具体代码为：

double focalLength = 800.0; // 焦距，决定透视强弱
double perspective = focalLength / (focalLength - pz);

// 屏幕坐标
double screenX = center.dx + px * perspective;
double screenY = center.dy + py * perspective;

// 点的大小也随透视缩放
double pointSize = basePointSize * perspective;

之后我们还需要增加一些效果，比如它让球体看起来像果冻一样的动画：

其实原理就是，在旋转之人为地修改了点的 x, z 坐标：

• sin(time...) 引入了周期性的波浪
• + y * 4 让波浪在球体上下不同高度处于不同相位（产生像蛇一样的扭动感）
• 通过 wobble 系数决定了波浪的振幅，如果为 0，offset 为 0，球体就是完美的圆形

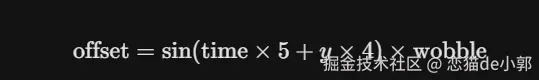
最后还有 TRAILS (拖尾) -> 改变绘制样式，实际上这不是物理模拟，而是视觉欺骗

具体是纤位：

• 当 trails == 0 时，使用 canvas.drawCircle 画圆点
• 当 trails > 0 时，使用 canvas.drawLine 画线，线的长度由 trails 参数乘以透视系数决定，因为球在水平旋转，我们在水平方向画一条短线，大脑就会自动脑补成"这是因为转太快留下的残影"

实际上我还在自己的个人主页上将上面了两种动画，让 AI 转化为 js+css ，让个人主页看起来更加花里胡哨：

星云动画

这是一个模拟星云旋转的动画效果，实际效果其实比动图里更加好看，它可以认为是在前面 Sprott B Attractor 的基础上更加复杂的实现，为了实现"粒子形成双核团块"的物理感，还需要模拟了星系动力学。

引力场模型

这里的粒子不再是简单的画圆，而是一种"受力"运动的效果，所以需要：

• 中心引力：提供基础的向心力
• 旋转棒引力：模拟双极引力场

另外还需要吸积盘模拟 (Accretion)，让粒子看起来围绕"黑洞"中心运动：

• 粒子不从中心喷出，而是生成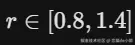在的外围圆盘
• 引入微小的摩擦力（velocity *= 0.9995）作为阻尼

让粒子因能量损耗，轨道逐渐衰减，从外围螺旋落入中心，并在途中被棒的引力捕获，这就产生了真实的"拖尾"和"聚拢"效果。

最后核心使用了多重正弦波叠加的湍流算法 (getTurbulence)，让粒子运动看起来像沸腾的岩浆，具有很强的生命力：

    Offset getTurbulence(int i, double phase, double t) {
      double speed = 2.0;
      double dx = 0.06 * sin(t * speed + phase) + 0.03 * cos(t * speed * 2.3 + i * 0.1);
      double dy = 0.06 * cos(t * speed * 1.5 + phase) + 0.03 * sin(t * speed * 1.9 + i * 0.1);
      double rotAngle = t * 0.5 * (i % 2 == 0 ? 1 : -1);
      double rx = dx * cos(rotAngle) - dy * sin(rotAngle);
      double ry = dx * sin(rotAngle) + dy * cos(rotAngle);
      return Offset(rx, ry);
    }

最后是让 30,000 个粒子配合 BlendMode.plus，在重叠处产生了高亮的能量感，模拟了星系的高密度区域，主要有：

• 使用 Float32List 存储数据，内存紧凑，访问极快

• 使用 canvas.drawRawPoints 批量绘制，这是 Flutter 中利用 GPU 渲染粒子的最高效方式

问题

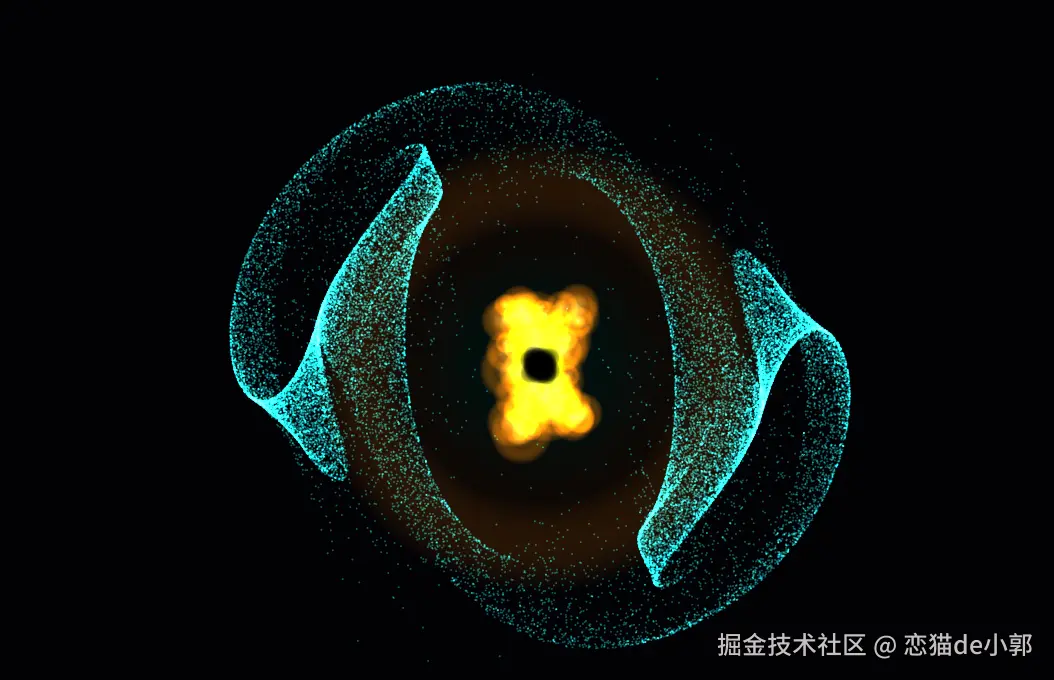
当然， AI 在实现时其实遇到了一个比较麻烦的问题：颜色的"插值陷阱"，有时候也称为 Uninitialized Tile Artifacts（未初始化瓦片伪影） , 具体为:

在 tile-based GPU（大多数移动 GPU 与 WebGL framebuffer）中，当某些 tile 区域在进入 blending/compositing 阶段之前 没有被正确清理（未写入有效像素），它们会以默认值（通常为黑色透明）参与加法混合，从而显示为黑块。

也就是出现了下方图片的几个透明黑块，黑块随着运动变化，时而明显，时而消失：

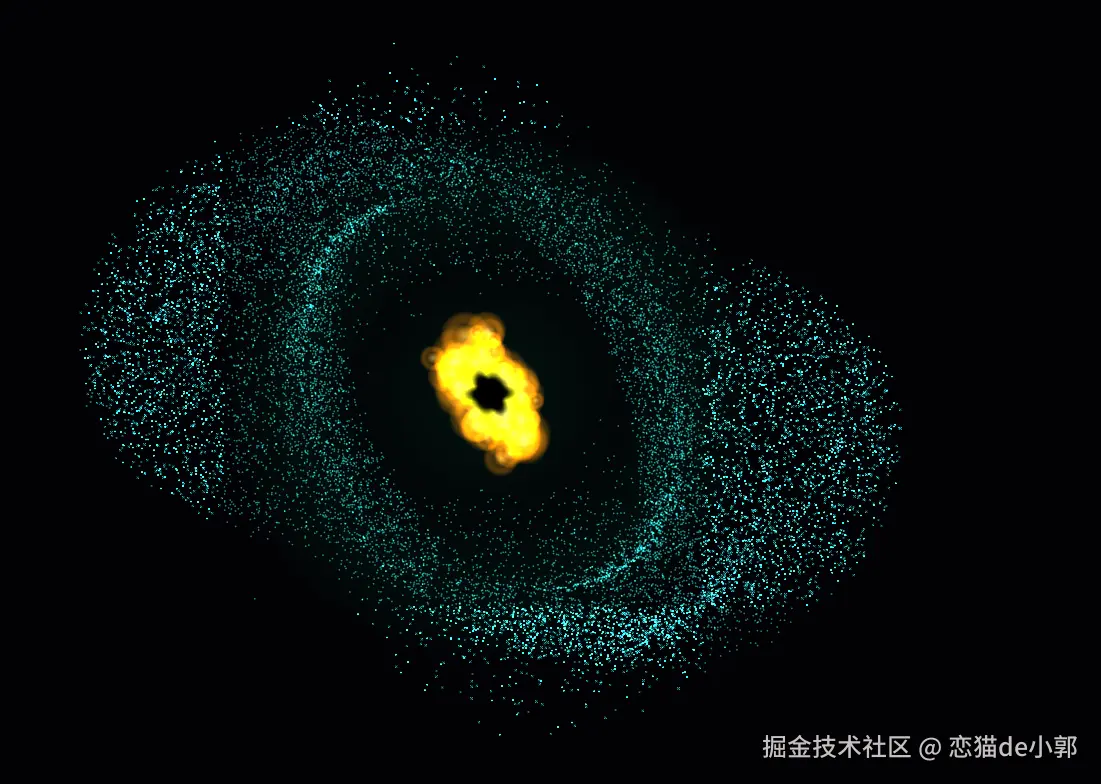
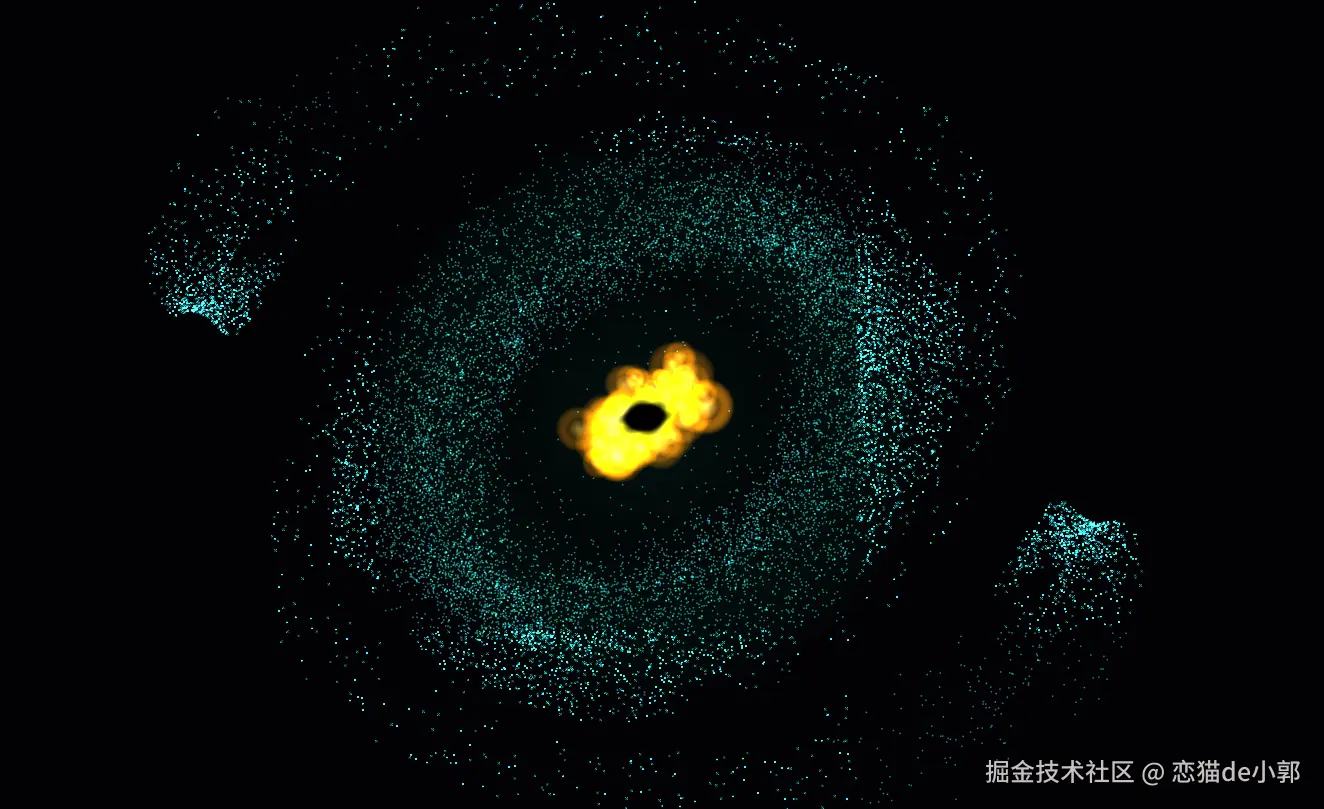
所以这里看到的"黑块"，实际上是 Canvas 绘制圆形时的 Bounding Box， 虽然代码命令计算机画一个圆，但计算机在底层是先画一个正方形区域，然后计算像素距离圆心的距离来填充颜色， 当这个正方形区域边缘的像素没有处理干净时，就会看到一个淡黑色的方框。

而在 Flutter中，代码里主要有：

• Colors.orange 的数据是：R=255, G=165, B=0, A=255
• Colors.transparent 的数据实际上是透明的黑色：R=0, G=0, B=0, A=0

猜测是，定义一个渐变从 橙色 -> 透明 时，计算机需要计算中间的过渡色，一般来说数学计算过程是这样的：

• 起点：亮橙色 (255, 165, 0, 255)
• 中间：半透明的深褐色 (128, 82, 0, 128) <- 可能出问题的地方
• 终点：透明黑色 (0, 0, 0, 0)

整个情况下，如果用默认的混合模式（SourceOver），Alpha 通道会把这个"深褐色"隐藏掉，因为它越来越透明。

而在实际实现上，在增加了中间区域的发光特效， 为了实现要求的"发光、高亮、高温"效果，AI 使用了 BlendMode.screen（滤色） 或 BlendMode.plus（相加）：

• 在这些混合模式下，RGB 值的亮度决定了最终画面
• 那个中间状态的"深褐色"，虽然 Alpha 很低，但它的 RGB 不是 0
• 在 Screen 模式下，这层淡淡的褐色会像一层薄纱一样叠在背景上，导致正方形区域显形

而 AI 在几次尝试修复里，一直没能修复问题：

• 尝试 A：使用 TileMode.decal（剪切模式）
  • 原理：告诉计算机"超出圆半径的像素直接扔掉，不要画"，避免渐变边缘在透明像素上产生 undefined 行为
  • 结果：没有效果
• 调整 Colors.transparent
  • 原理：试图让渐变变得更淡。
  • 结果 ：方块变淡了，但依然存在，因为只要终点是 Colors.transparent，中间插值就一定包含"黑色成分"。
• 尝试 C：BlendMode 层面的修复
  • 原理：尝试去掉 Plus ，Plus 混合会创建 offscreen buffer，透明像素的初始值要么是黑，要么是不确定；如果深层次变换后参与合成，就会以"脏块"形式出现，所以替换为在某些层用 srcOver，单独隔离 blob / halo / blackhole 的加法混合，调整合成顺序等
  • 结果： 黑块依旧出现
• 尝试 D：Canvas 层面的修复
  • 原理 ：saveLayer + clear 强制透明背景，用真实透明 offscreen 替代 GPU 依赖背景，去掉 RadialGradient transform，目的是完全控制合成区域，阻止脏像素泄漏
  • 结果： 黑块依旧出现

这一切的问题看起来都是 GPU tile buffer 没有正确清除，以至于换个 AI ，从 Gemini 3 Pro 换到 GPT 5，它都觉得："不是你，不是我，不是实现错误" ：

那为什么最后还是解决了呢？其实是投机取巧，这里不再调整 BlendMode 或 Gradient ，而是通过叠加多层不同相位的蠕动来实现中间的橙色呼吸效果， 通过 "弹性形变"不仅仅是位置偏移，还可以根据时间修改每个小团块的大小（Size）和拉伸比（Scale）。

也就是问题其实没解决，只是最终换了个路子，实际上 AI 一直在死磕解决，但是换了几个 AI 多次尝试后依然无果，所以核心应该还是底层支持上的伪影问题，所以最终我主动让 AI 换了种实现，其实这也是程序猿在 AI 时代的作用，毕竟 AI 还很擅长瞎扯，这些回答每一个能用的：

最后，不得不说，AI 在数学了领域是真的强大。

链接

代码在下方连接，感兴趣的可以自取：

• github.com/CarGuo/gsy_...