目录
[1 高效注意力机制](#1 高效注意力机制)
[1.1 稀疏化与局部性](#1.1 稀疏化与局部性)
[1.2 低秩与核化近似](#1.2 低秩与核化近似)
[1.3 下采样](#1.3 下采样)
[1.4 其他](#1.4 其他)
[2 布尔可满足性问题](#2 布尔可满足性问题)
[3 量子三大逻辑门实现](#3 量子三大逻辑门实现)
[3.1 量子 AND](#3.1 量子 AND)
[3.2 量子 OR](#3.2 量子 OR)
[3.3 量子 NOT](#3.3 量子 NOT)
[4 总结](#4 总结)
摘要
本周首先学习了高效注意力机制,了解了几种实现路径的思想与具体方法,包括稀疏注意力、线性注意力等;其次了解了布尔可满足性问题的定义与重要性;最后回顾了量子三大基本逻辑门的计算,并进行了代码实现。
Abstract
This week, I first studied efficient attention mechanisms, learning the concepts and specific methods of several implementation approaches, including sparse attention and linear attention. Secondly, I explored the definition and importance of the Boolean satisfiability problem. Finally, I reviewed the computations of the three fundamental quantum logic gates and implemented them in code.
1 高效注意力机制
在之前的学习中了解到,计算注意力分数的方法主要包括加性注意力(Additive Attention)、点积注意力(Dot-Product Attention)及缩放点积注意力(Scaled Dot-Product Attention)、余弦相似度注意力(Cosine Similarity Attention)还有双线性注意力(Bilinear Attention)。除了加性注意力以外,其他的方法都涉及了Q与K向量的点积运算,其复杂度为 ,这导致当输入序列变长时,计算量大以及内存占用高的问题也会随之明显。
高效注意力机制的目标就是在保持注意力核心优势(全局上下文建模)的同时,将其复杂度从 降低到
或
以显著降低计算和内存开销。
1.1 稀疏化与局部性
稀疏化与局部性的核心思想主要在于,不是所有 token 之间都需要进行交互。这种方式会强制让每个 token 只关注一小部分重要的 token,而非全部。
体现这种思想的一种技术是局部窗口注意力,其做法是将输入序列划分为多个不重叠或重叠的局部窗口,只在每个窗口内计算注意力,此时复杂度降为 (w 为窗口大小,当其固定时,复杂度会进一步降为
)。这种技术复杂度低,且可处理任意长度的序列,但每个token只能看到对应窗口内的其他token,难以建立跨窗口的全局依赖关系,窗口边缘的token可能也无法充分交互。
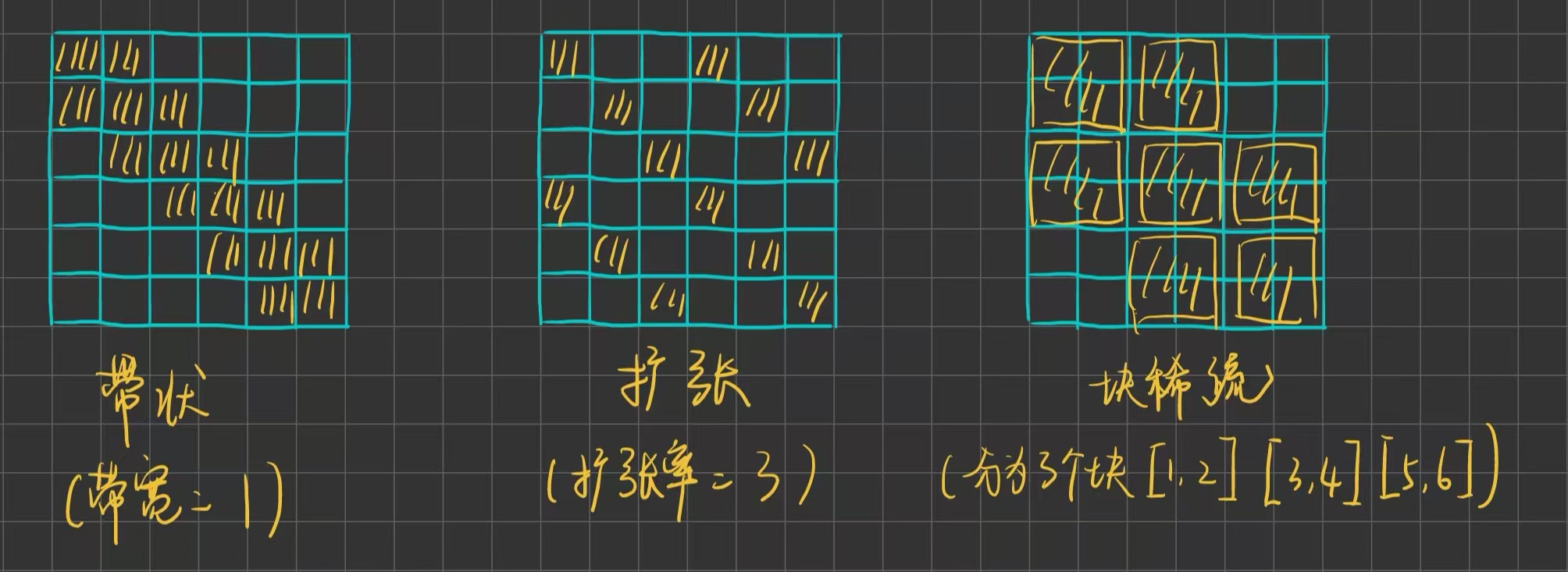
另一种技术则是设计固定的、稀疏的注意力模式**,**如带状注意力(Band Attention,关注邻近元素)、扩张注意力(Dilated Attention,关注固定间隔的元素)以及块稀疏注意力(Block Sparse Attention,关注特定块)等。它通过减少计算注意力的位置对数量,显著降低了计算和内存复杂度,同时也面临着信息流动受限、模式设计复杂和硬件效率等挑战。
1.2 低秩与核化近似
理论上,一个标准的缩放点积注意力矩阵 A 计算如下:
Q, K的维度通常均为 ,且矩阵乘积的秩不大于任何因子矩阵的秩**,** 而特征维度
通常又远低于序列长度 n ,故这个
的矩阵是的秩会被限制在了远小于 n 的维度
上,进而可以通过一些技巧来近似这个矩阵,而无需显式地计算它。
线性注意力的做法就是通过巧妙的数学变换(通常是核函数),将 的计算顺序改为
,这样就不再需要生成
的中间矩阵。它的复杂度为 O(n),同时有多种实现方式,但在某些任务上可能略逊于标准注意力。
另一种方法是Nyström方法。它最初用于积分方程的特征函数近似,后来被应用于机器学习中的核方法。其核心思想是通过采样少量 landmark 点(也称为锚点或种子点)来重建整个注意力矩阵。
这种方法有坚实的数学理论基础,可以根据计算预算灵活调整地标点数量,在地标点选择不理想时也能保持一定的稳定性,不过地标点选择对性能影响还是比较大,而且实现相对复杂。
1.3 下采样
下采样的核心思想都是通过减少注意力计算中的键值对数量,从而降低计算复杂度。
实际上,前面的线性注意力与Nyström方法也可以看作是对注意力矩阵进行下采样。下采样的优点在于能够在保留全局信息的同时显著降低计算量,还具有良好的可扩展性。缺点是一方面不同的下采样方法对性能有影响,而且不管哪种下采样方法都无可避免的会丢失部分信息;另一方面上采样过程可能引入噪声或误差。
其具体的步骤主要包括下采样、注意力计算与上采样(可选)。下采样的策略包括池化(平均池化与最大池化)下采样、卷积下采样、学习式下采样与聚类。根据采取的不同策略,其注意力计算模式又可分为两种,即完全在下采样序列上计算注意力与仅对Key和Value下采样。前者将Query、Key、Value都下采样到长度m,然后计算m×m的注意力矩阵,输出长度为m的序列,如果需要,再通过上采样恢复到原有长度n;后者则只对Key和Value进行下采样,Query保持原始序列长度n,然后计算n×m的注意力矩阵,输出长度为n的序列,无需上采样。
1.4 其他
除了前面的几种主要方法,还可以将注意力与来自其他领域的成熟思想结合。比如结合RNN的门控与循环机制,以递归的方式更新隐藏状态,从而避免计算全注意力;或者使用本质上为线性复杂度的状态空间模型(如S5)来替代注意力,进行长序列建模。
另外,不改变注意力算法的数学定义,而是通过极致的工程优化,使其在硬件上运行得更快也不失为一种有效方式。比如FlashAttention,就通过分块计算和避免将巨大的注意力矩阵写入显存,在 GPU 上极大地加速了标准注意力的计算,还降低了内存占用。
2 布尔可满足性问题
布尔可满足性问题,也称SAT问题,是指给定一个布尔表达式,判断是否存在一组布尔变量的赋值,使得整个表达式的求值结果为 True。如果存在则称这个布尔表达式是可满足的,反之则不可满足。
上述定义中,布尔变量是最基本的元素,只能取True/False(真或假)的值,通常用字母表示;布尔表达式是由布尔变量通过逻辑运算符连接而成的式子,最常见的运算符包括与(,AND)、或(
,OR)、非(¬,NOT);为了系统化地研究SAT问题,通常会将布尔表达式写成一种标准形式,即合取范式,它由若干个子句通过"与"连接而成,当且仅当其所有子句为真时,合取范式才为真。
SAT问题是第一个被证明的NP完全问题,这意味着如果存在一个高效的算法来解决SAT问题,那么所有NP问题都可以被高效解决。它的应用也十分广泛,许多现实世界的问题都可以自然地转化为SAT问题来求解,比如课程表安排。
SAT问题的特殊类型被定义为K-SAT问题,即合取范式中的每个子句恰好包含k个布尔变量,当k大于等于三时,k-SAT都是NP完全的。
p.s. P类问题指能在多项式时间内解决的决策问题,NP类则指能在多项式时间内验证解的决策问题,NP困难问题是至少和NP中最难的问题一样难的问题,NP完全指的是既属于NP又是NP困难的问题。
下周即将学习的Grover算法就为解决SAT问题提供了一个量子加速方案。
3 量子三大逻辑门实现
3.1 量子 AND
量子AND门通过使用一个额外的辅助比特和一个Toffoli门(也叫CCNOT门,控控非)实现,故一共有两个控制量子比特与一个目标量子比特,当两个控制量子比特都为1时,就对目标量子比特进行翻转(NOT操作)。
其真值表如下:
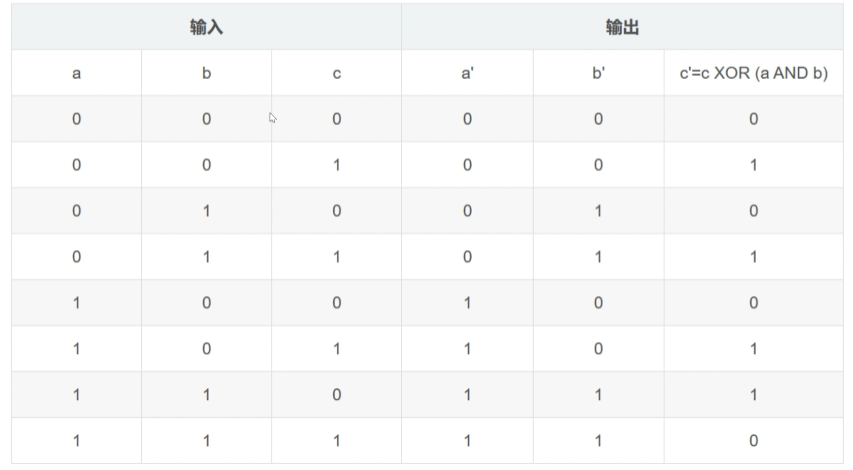
实现代码:
python
from qiskit import QuantumCircuit
circ = QuantumCircuit(3) #创建一个包含3个量子比特的量子电路,索引分别为0,1,2
circ.ccx(0, 1, 2) #经过CCNOT门,0,1,2作为量子比特索引分别对应控制比特1,控制比特2与目标比特
print(circ.draw())其量子电路如下:
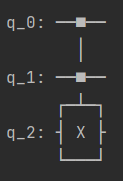
3.2 量子 OR
OR 门与 AND 门结构相似,可以借助其间接实现,其过程为:先将两个控制比特(A、B)和目标比特都进行翻转,然后对它们应用Toffoli门,那么将会输出 ,
和
,由德摩根定律可得:
如果想要原始的控制量子比特,可以再对其进行翻转。
实现代码:
python
from qiskit import QuantumCircuit
circ = QuantumCircuit(3)
circ.x(0) #翻转
circ.x(1)
circ.x(2)
circ.ccx(0, 1, 2)
circ.x(0)
circ.x(1)
print(circ.draw())其量子电路如下:
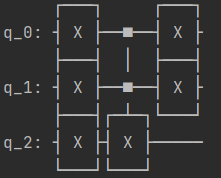
3.3 量子 NOT
量子NOT门的作用就对应前文中的翻转,利用X门进行实现,较为简单
代码如下:
python
from qiskit import QuantumCircuit
circ = QuantumCircuit(2)
circ.x(0) #翻转
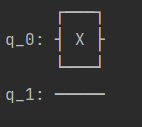
print(circ.draw())量子电路如下:
4 总结
本周的学习主要属于过渡期,一方面通过对高效注意力机制的学习,回顾了前面知识的同时也为后面阅读论文,进一步学习transfomer的变体与改进打基础;另一方面,通过量子基础逻辑门的实现巩固前面所学,同时了解布尔可满足性问题,方便后续Grover算法的学习。