二叉树的非递归后序遍历-双栈法

文章目录

- 方法概述
- 详细实现步骤
- - [1. 数据结构初始化](#1. 数据结构初始化)
  - [2. 主要遍历过程](#2. 主要遍历过程)
  - [3. 提取最终结果](#3. 提取最终结果)
- 为什么这样能实现后序遍历？
- - 栈的操作逻辑
- 示例演示
- - 执行过程：
- 算法特点

题目背景：力扣145. 二叉树的后序遍历

示例：
复制代码
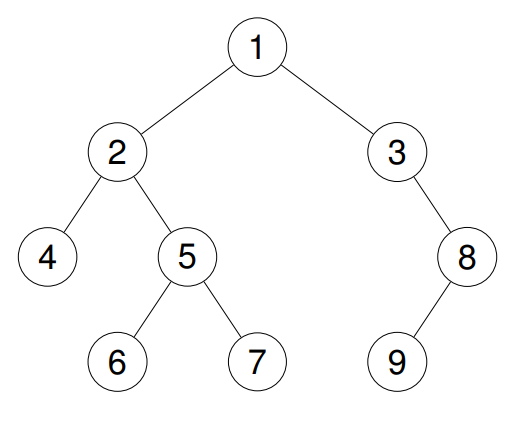
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[4,6,7,5,2,9,8,3,1]
解释：

后序遍历要求按照【左子树 → 右子树 → 根节点】的顺序访问二叉树的所有节点。双栈法，通过两个栈的配合来完成逆序访问，虽然同样是使用栈解决二叉树非递归后序遍历，但是理解起来能简单不少，且将"栈"的特性发挥得淋漓尽致，也有巧妙之处

方法概述

双栈法的基本思路是：

使用第一个栈(s1)进行前序遍历的变形（根→右→左）
将遍历结果存入第二个栈(s2)
最终从s2弹出的顺序即为后序遍历结果（左→右→根）

详细实现步骤

1. 数据结构初始化

java 复制代码

ArrayDeque<TreeNode> s1 = new ArrayDeque<>(); // 辅助栈，实际上是"特殊的"前序遍历
ArrayDeque<TreeNode> s2 = new ArrayDeque<>();
s1.push(root);  // 将根节点压入s1

2. 主要遍历过程

java 复制代码

while (!s1.isEmpty()) {
    TreeNode node = s1.pop();  // 从s1弹出当前节点
    s2.push(node);            // 将节点压入s2
  
    // 关键操作：先压左子节点，再压右子节点，这样未来pop的时候才能先pop右子树，再左子树
    if (node.left != null) {
        s1.push(node.left);
    }
    if (node.right != null) {
        s1.push(node.right);
    }
}

3. 提取最终结果

java 复制代码

while (!s2.isEmpty()) {
    ans.add(s2.pop().val);  // 从s2弹出即为后序遍历结果
}

为什么这样能实现后序遍历？

栈的操作逻辑

第一次压栈（s1）: 构建「根→右→左」序列
- 根节点首先入栈
- 右子节点后入栈（位于左子节点上方）
- 左子节点先入栈（位于右子节点下方）
第二次压栈（s2） : 反转顺序
- 当从s1弹出节点时，顺序是「根→右→左」
- 压入s2后，顺序变为「左→右→根」（栈的反转特性）
最终弹出（s2）: 得到正确后序遍历
- 从s2弹出的顺序正好是「左→右→根」

示例演示

对于以下二叉树：

复制代码

执行过程：

s1 = [1], s2 = []
弹出1 → s2 = [1], 压入2和3 → s1 = [2, 3]
弹出3 → s2 = [1, 3], 3的左右都为null, 没有可以压入的
弹出2 → s2 = [1, 3, 2] , 压入4和5 → s1 = [4, 5]
弹出5 → s2 = [1, 3, 2, 5], 同理，5没有可以压入的子节点
弹出4 → s2 = [1, 3, 2, 5, 4], s1空，结束while

最终从s2弹出的顺序：4 → 5 → 2 → 3 → 1，即后序遍历结果。

算法特点

时间复杂度: O(n)，每个节点访问两次
空间复杂度: O(n)，最坏情况下需要两个栈的空间
优点: 逻辑清晰，容易理解和实现
适用性: 适用于各种二叉树结构

双栈法虽然是使用栈，但是相比于使用单个栈进行复杂节点处理要简单很多