算法竞赛中的堆

一.堆的概念
二.堆的模拟实现
- 1.堆的基础存储结构
- 2.堆的核心操作原理（大顶堆）
- - [2.1 向上调整（up函数）：插入元素后恢复堆性质](#2.1 向上调整（up函数）：插入元素后恢复堆性质)
  - [2.2 向下调整（down函数）：删除堆顶后恢复堆性质](#2.2 向下调整（down函数）：删除堆顶后恢复堆性质)
  - [2.3 插入元素（push函数）](#2.3 插入元素（push函数）)
  - [2.4 删除堆顶（pop函数）](#2.4 删除堆顶（pop函数）)
  - [2.5 辅助操作（top和size）](#2.5 辅助操作（top和size）)
- [3. 测试函数（test01）：堆排序演示](#3. 测试函数（test01）：堆排序演示)
- - 执行过程示例：
- 4.核心总结
三.priotiy_queue
- [1. 基本用法](#1. 基本用法)
- [2. 常用操作（O(log n) 时间）](#2. 常用操作（O(log n) 时间）)
- [3. 小根堆的实现](#3. 小根堆的实现)
- [4. 竞赛典型应用](#4. 竞赛典型应用)
- [5. 注意点](#5. 注意点)
四.习题：【模板】堆
- 1.题目
[五.第 k 小](#五.第 k 小)
- 1.题目
- 2.解题思路
- - [2.1 问题分析](#2.1 问题分析)
  - [2.2 核心思路：用大根堆维护"前k小的数"](#2.2 核心思路：用大根堆维护“前k小的数”)
  - [2.3 代码对应逻辑](#2.3 代码对应逻辑)
  - [2.4 时间复杂度](#2.4 时间复杂度)
- 3.参考代码
六.习题：除2！
- 1.题目
- 2.解题思路
- - [2.1 解题思路](#2.1 解题思路)
  - [2.2 核心亮点](#2.2 核心亮点)
- 3.参考代码
七.习题：最小函数值
- 1.题目
- 2.解题思路
- - [2.1 问题分析（结合图片示例）](#2.1 问题分析（结合图片示例）)
  - [2.2 核心思路（对应图片"堆+单调性"解法）](#2.2 核心思路（对应图片“堆+单调性”解法）)
  - [2.3 代码对应逻辑（匹配图片元素）](#2.3 代码对应逻辑（匹配图片元素）)
  - [2.4 时间复杂度](#2.4 时间复杂度)
- 3.参考代码
八.习题：序列合并
- 1.题目
- 2.解题思路
- - [2.1 问题分析](#2.1 问题分析)
  - [2.2 核心思路（小根堆实现多路归并）](#2.2 核心思路（小根堆实现多路归并）)
  - [2.3 代码对应逻辑](#2.3 代码对应逻辑)
  - [2.4 时间复杂度](#2.4 时间复杂度)
- 3.参考代码

Hello，小伙伴们！又到了咱们一起捣鼓代码的时间啦！💪 把生活调成热情模式，带着满满的能量钻进编程的奇妙世界吧------今天也要写出超酷的代码，冲鸭！🚀

我的博客主页：喜欢吃燃面
我的专栏：《C语言》，《C语言之数据结构》，《C++》，《Linux学习笔记》
感谢你点开这篇博客呀！真心希望这些内容能给你带来实实在在的帮助～如果你有任何想法或疑问，非常欢迎一起交流探讨，咱们互相学习、共同进步，在编程路上结伴成长呀！

一.堆的概念

堆是一种完全二叉树结构 的优先队列，核心特性是"父节点与子节点的优先级满足固定关系"，分为两种类型：

大根堆：父节点的值 ≥ 子节点的值（堆顶是整个堆的最大值）；
小根堆：父节点的值 ≤ 子节点的值（堆顶是整个堆的最小值）。

堆的核心操作（基于数组实现，利用完全二叉树的索引特性：父节点索引=子节点索引/2，左子节点索引=父节点索引×2）：

插入：元素加到堆尾，再"向上调整"（与父节点比较，不符合堆性质则交换）；
删除堆顶：堆顶与堆尾元素交换后删除堆尾，再对新堆顶"向下调整"（与子节点比较，不符合堆性质则交换）；
取堆顶：直接获取堆的第一个元素（最大值/最小值）。

堆的典型应用：

高效找最值（时间复杂度O(1)取堆顶）；
排序（堆排序，时间复杂度O(n log n)）；
多路归并（如合并多个有序序列、找前k小/大元素）。

二.堆的模拟实现

以 大顶堆（大根堆）的完整模拟实现 为例，基于数组（1-based索引）存储完全二叉树，核心是通过 up（向上调整）和 down（向下调整）维护堆的性质。下面从「堆的存储结构」「核心操作原理」「代码逐部分讲解」三个维度，详细拆解堆的模拟实现：

1.堆的基础存储结构

由于堆的本质是「完全二叉树」，所以为了方便计算父/子节点关系，代码采用顺序存储即：1-based索引（数组从下标1开始存储元素），核心索引规律：

对于下标为 i 的节点（父节点）：
- 左子节点下标 = i * 2
- 右子节点下标 = i * 2 + 1
对于下标为 j 的节点（子节点）：
- 父节点下标 = j / 2（整数除法）

代码中存储相关定义：

cpp 复制代码

const int N = 1e4 + 10;  // 堆的最大容量（最多存1e4个元素）
int heap[N];              // 堆的数组存储（heap[1]是堆顶，heap[0]闲置）
int n;                    // 堆中当前元素个数（动态维护）

2.堆的核心操作原理（大顶堆）

大顶堆的核心性质：所有父节点的值 ≥ 子节点的值 ，堆顶（heap[1]）是最大值。所有操作的本质都是「先修改元素，再通过调整恢复堆性质」，核心调整函数是 up 和 down。

2.1 向上调整（up函数）：插入元素后恢复堆性质

场景：新元素插入到堆尾（保证完全二叉树结构），但可能比父节点大，破坏大顶堆性质，需要向上"冒泡"。

输入参数 child：新元素的下标（堆尾下标 n）
操作步骤：
1. 计算父节点下标 parent = child / 2；
2. 若父节点存在（parent ≥ 1）且子节点值 > 父节点值，交换两者；
3. 把子节点下标更新为父节点下标，重复步骤1-2，直到父节点更大或到达堆顶。

代码对应逻辑：

cpp 复制代码

void up(int child) {
    int parent = child / 2;
    while (parent >= 1 && heap[child] > heap[parent]) {  // 子>父，破坏大顶堆
        swap(heap[child], heap[parent]);  // 交换修复
        child = parent;                  // 子节点上移到父节点位置
        parent = child / 2;              // 重新计算新的父节点
    }
}

2.2 向下调整（down函数）：删除堆顶后恢复堆性质

场景：堆顶元素删除后，用堆尾元素填充堆顶（保证完全二叉树结构），但新堆顶可能比子节点小，破坏大顶堆性质，需要向下"沉底"。

输入参数 parent：需要调整的父节点下标（新堆顶下标 1）
操作步骤：
1. 计算左子节点下标 child = parent * 2；
2. 若右子节点存在（child+1 ≤ n）且右子节点 > 左子节点，选择更大的右子节点作为比较对象；
3. 若子节点值 > 父节点值，交换两者；
4. 把父节点下标更新为子节点下标，重复步骤1-3，直到子节点更小或到达堆底。

代码对应逻辑：

cpp 复制代码

void down(int parent) {
    int child = parent * 2;  // 先默认左子节点是更大的子节点
    while (child <= n) {     // 子节点存在（未到堆底）
        // 选左、右子节点中更大的那个
        if (child + 1 <= n && heap[child + 1] > heap[child])
            child++;
        // 子>父，破坏大顶堆，交换修复
        if (heap[child] > heap[parent]) {
            swap(heap[child], heap[parent]);
            parent = child;  // 父节点下移到子节点位置
            child = parent * 2;  // 重新计算新的左子节点
        } else {
            break;  // 父节点≥子节点，堆性质正常，退出
        }
    }
}

2.3 插入元素（push函数）

基于 up 函数实现，步骤：

把新元素放到堆尾（heap[++n] = x），堆大小 n 加1；
对新元素执行 up 调整，恢复大顶堆性质。

代码：

cpp 复制代码

void push(int x) {
    heap[++n] = x;  // 堆尾添加元素，n自增
    up(n);          // 向上调整新元素
}

2.4 删除堆顶（pop函数）

基于 down 函数实现，步骤：

把堆顶（heap[1]）和堆尾（heap[n]）交换（用堆尾元素覆盖堆顶）；
堆大小 n 减1（间接删除原堆顶元素）；
对新堆顶（原堆尾元素）执行 down 调整，恢复大顶堆性质。

代码：

cpp 复制代码

void pop() {
    swap(heap[1], heap[n]);  // 堆顶与堆尾交换
    n--;                     // 删除堆尾（原堆顶）
    down(1);                 // 向下调整新堆顶
}

2.5 辅助操作（top和size）

top()：直接返回堆顶元素（heap[1]），O(1) 时间；
size()：返回当前堆中元素个数 n，O(1) 时间。

代码：

cpp 复制代码

int top() { return heap[1]; }  // 大顶堆堆顶是最大值
int size() { return n; }       // 获取堆大小

3. 测试函数（test01）：堆排序演示

test01 函数通过「构建堆 + 弹出堆顶」实现 堆排序（从大到小），步骤：

定义测试数组 arr[7] = {0,3,1,4,1,5,9}（下标0闲置，实际元素是3,1,4,1,5,9）；
循环将元素插入堆（push），构建大顶堆；
循环弹出堆顶（pop）并输出，每次弹出的都是当前堆的最大值，最终输出排序结果。

执行过程示例：

插入所有元素后，堆的结构（大顶堆）：堆顶是9（heap[1]=9）；
第一次弹出9，输出9；堆尾元素1覆盖堆顶，down调整后堆顶是5；
第二次弹出5，输出5；堆尾元素1覆盖堆顶，down调整后堆顶是4；
依次类推，最终输出：9 5 4 3 1 1（从大到小排序）。

4.核心总结

堆的模拟实现核心是「数组存储完全二叉树 + up/down 调整维护堆性质」：

1-based索引是关键：简化父/子节点的计算；
up调整：解决"新元素太大"的问题（插入场景）；
down调整：解决"父节点太小"的问题（删除堆顶场景）；
基于堆的操作可实现堆排序、TopK问题等经典应用，时间复杂度均为 O(n log n)。

这段代码完整覆盖了大顶堆的核心功能，修改 up 和 down 中的比较符号（> 改为 <），即可快速实现小顶堆。

三.priotiy_queue

在算法竞赛中，优先队列（priority_queue） 是基于「堆」实现的容器，核心作用是自动维护元素的优先级，快速获取最值，是竞赛中高频工具之一。

1. 基本用法

头文件：#include <queue>

默认是大根堆（堆顶为最大值），定义格式：

cpp 复制代码

priority_queue<int> heap;  // 大根堆（默认）

2. 常用操作（O(log n) 时间）

push(x)：插入元素 x，自动调整堆；
pop()：删除堆顶元素；
top()：获取堆顶元素（大根堆是最大值，小根堆是最小值）；
size()：返回元素个数；
empty()：判断是否为空。

3. 小根堆的实现

通过修改模板参数，实现小根堆（堆顶为最小值）：

cpp 复制代码

// 方式1：greater<T>（需包含 <functional>）
priority_queue<int, vector<int>, greater<int>> heap;

// 方式2：自定义结构体+重载<（适用于复杂元素）
struct node {
    int val;
    bool operator<(const node& x) const {
        return val > x.val;  // 小根堆：val小的优先级高
    }
};
priority_queue<node> heap;

4. 竞赛典型应用

（其实就是堆的应用）

TopK问题：找前k小/大元素（用堆维护k个元素）；
多路归并：合并多个有序序列（如找n个函数的前m小值）；
贪心算法：按优先级选择最优解（如任务调度、区间问题）；
堆排序：快速实现O(n log n)排序。

5. 注意点

优先队列是黑盒，不支持随机访问，只能操作堆顶；
复杂元素（如结构体）必须重载<运算符，否则无法比较；
时间复杂度：单次操作O(log n)，适合大数据量（n≤1e5/1e6）。

注：在算法竞赛中需要使用堆结构时，直接使用priority_queue即可，无需自己造轮子。

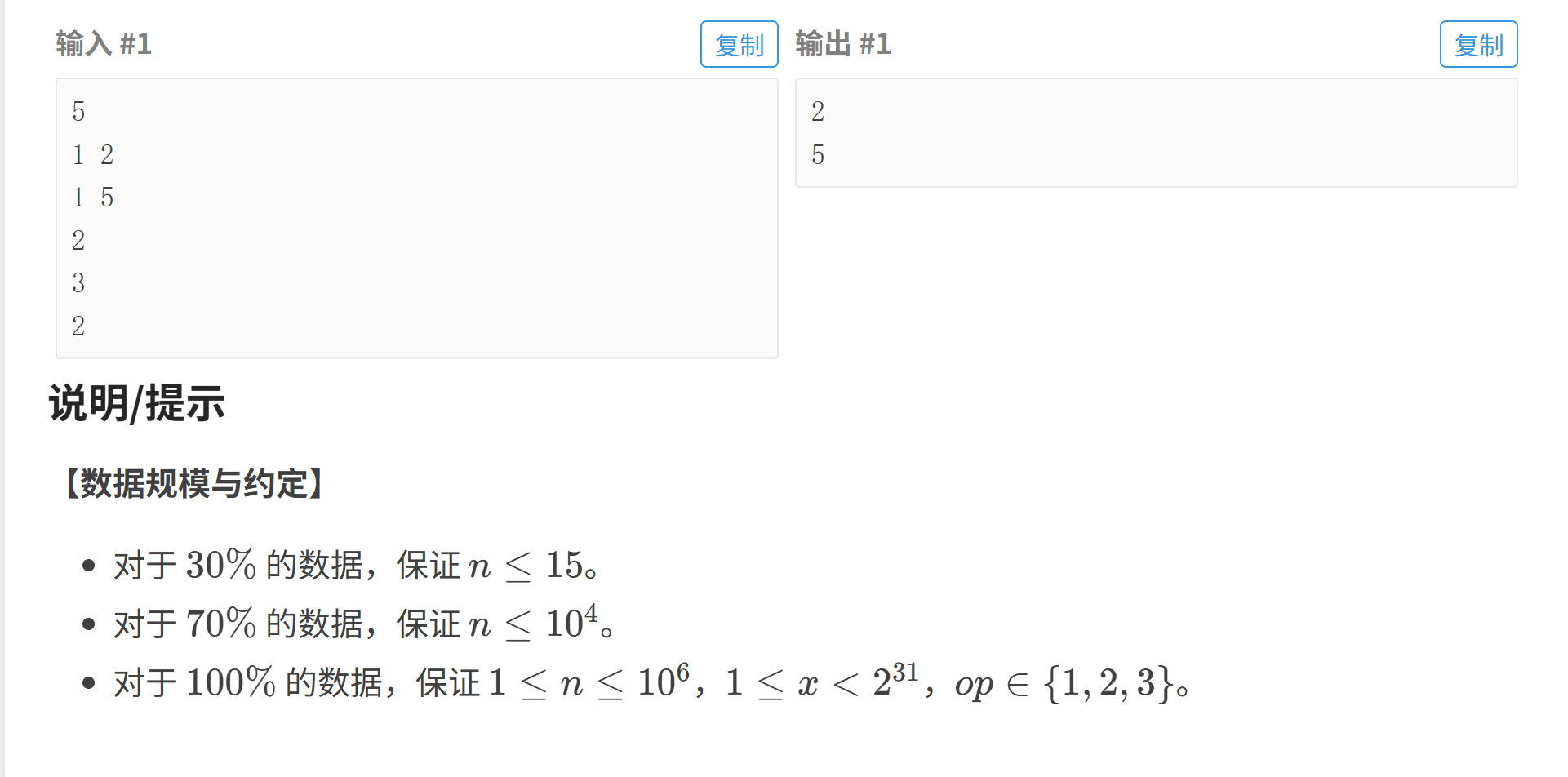
四.习题：【模板】堆

1.题目

【模板】堆

注：由于本题较为基础和简单只提供题目

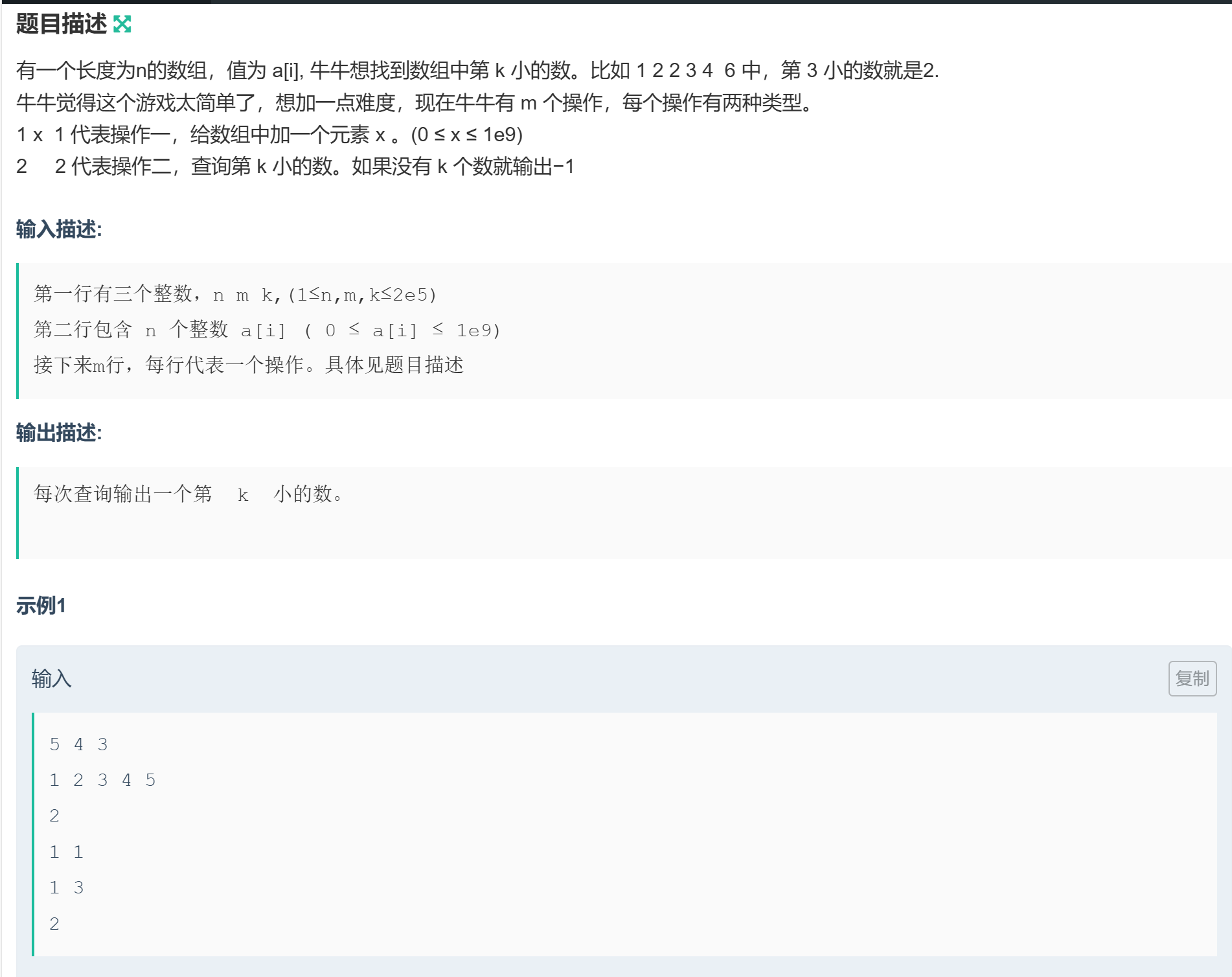
五.第 k 小

1.题目

第 k 小

2.解题思路

这道题的核心是动态维护数组中第k小的数 ，需要高效处理"添加元素"和"查询第k小"两种操作,所以采用了大根堆的巧妙解法。

2.1 问题分析

题目要求：

初始数组有n个元素，支持m次操作（添加元素/查询第k小）；
查询时，若数组元素不足k个则输出-1，否则输出第k小的数。

直接对数组排序+维护的话，每次添加元素后重新排序的时间复杂度太高（(O((n+m)*log(n+m)))），无法处理 (n,m <=2e5) 的数据规模。

2.2 核心思路：用大根堆维护"前k小的数"

我们只需要保留数组中最小的k个数，并通过大根堆管理这k个数：

大根堆的特性是堆顶是堆中最大的数；
若堆中元素数量≤k：直接将新元素加入堆；
若堆中元素数量>k：加入新元素后，弹出堆顶（最大的数），保证堆中始终是当前数组中最小的k个数；
查询时，若堆的大小等于k，堆顶就是第k小的数（因为堆里是最小的k个数，堆顶是这k个数中最大的，即全局第k小）；若堆大小不足k，输出-1。

2.3 代码对应逻辑

初始化堆：
- 遍历初始数组的n个元素，依次加入大根堆；
- 每次加入后，若堆大小超过k，弹出堆顶，确保堆中是当前最小的k个数。
处理m次操作：
- 操作1（添加元素x）：将x加入堆，若堆大小超过k则弹出堆顶；
- 操作2（查询）：若堆大小等于k，输出堆顶（第k小的数）；否则输出-1。

2.4 时间复杂度

每个元素的"入堆+出堆"操作是 (O(\log k))；
整体时间复杂度是 (O((n+m)\log k))，(k \leq 2e5) 时，(\log k) 约为20，能轻松处理2e5规模的数据。

3.参考代码

cpp 复制代码

```cpp
#include<iostream>
#include<queue>
using namespace std;

priority_queue<int> heap;  // 大根堆：堆顶为堆中最大值

int main()
{
    int n, m, k;
    cin >> n >> m >> k;  // n：初始元素数；m：操作数；k：目标（查询第k小数）

    // 初始化：维护前k小的数（堆中始终保留最小的k个）
    while(n--)
    {
        int x; cin >> x;
        heap.push(x);  // 新元素入堆
        if(heap.size() > k) heap.pop();  // 超过k个则删最大的，保证堆存最小k个
    }

    // 处理m次操作
    while(m--)
    {
        int op; cin >> op;
        if(op == 1)  // 操作1：添加元素x
        {
            int x; cin >> x;
            heap.push(x);
            if(heap.size() > k) heap.pop();  // 维持堆大小≤k
        }
        else if(op == 2)  // 操作2：查询第k小数
        {
            // 堆满k个时，堆顶是第k小（最小k个中的最大值）；否则输出-1
            cout << (heap.size() == k ? heap.top() : -1) << endl;
        }
    }
    return 0;
}

六.习题：除2！

除2！

1.题目

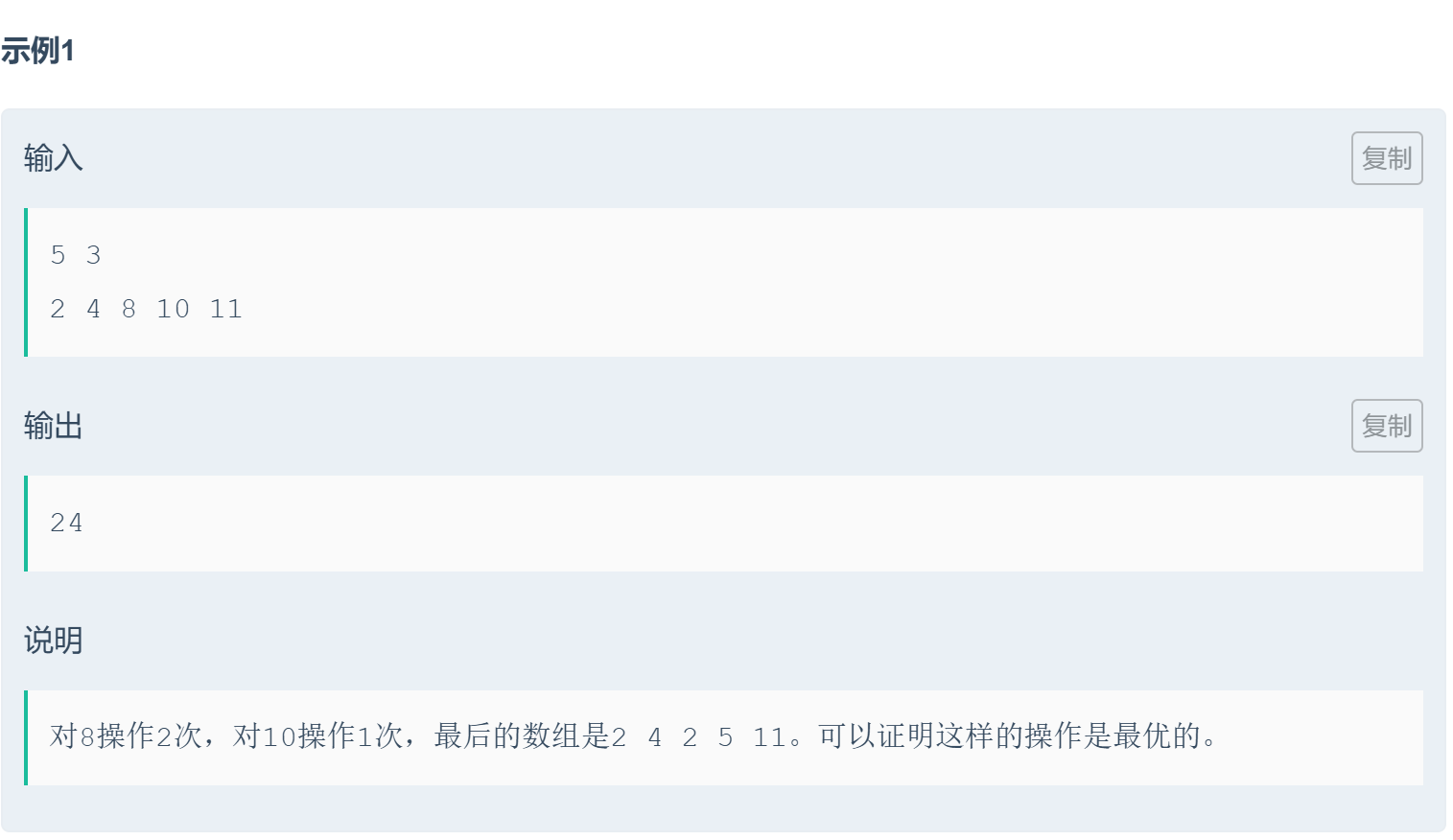
2.解题思路

核心是 "对偶数进行最多k次减半操作，最终计算所有数字的总和"。

2.1 解题思路

分类处理初始数字：
- 输入n个数字，奇数直接加入结果总和（奇数减半后可能变偶数，但题目允许的操作是"减半"，无需特殊限制，直接累加即可）；
- 偶数存入大根堆（优先处理大偶数，因为大偶数减半的"收益"更高，且题目无额外限制，按贪心思路先处理大数不影响最终总和）。
执行k次减半操作：
- 每次从堆顶取出最大的偶数，减半处理；
- 减半后若变成奇数，直接加入总和；若仍为偶数，放回堆中（可能后续继续减半）；
- 操作次数用完（k=0）或堆为空（无偶数可处理）时停止。
累加剩余偶数：
- 操作结束后，将堆中未处理的所有偶数加入总和，输出最终结果。

2.2 核心亮点

用大根堆保证每次处理当前最大的偶数，逻辑清晰且高效（时间复杂度O(n log n + k log n)，适配n≤1e6的规模）；
分类处理奇偶数，避免无效操作，简化逻辑。

3.参考代码

cpp 复制代码

#include<iostream>
#include<queue>
using namespace std;

const int N=1e6+10;  // 数据规模上限
priority_queue<int> heap;  // 大根堆：存偶数（优先处理大偶数）
long int ret;  // 结果总和

int main()
{
    int n,k;cin>>n>>k;  // n：数字总数；k：最多可执行的减半操作次数
    for(int i=1;i<=n;i++)
    {
        int x;cin>>x;
        if(x%2==0) heap.push(x);  // 偶数入堆
        else ret+=x;  // 奇数直接累加（不参与减半）
    }

    // 执行最多k次减半操作（堆非空时）
    while(k--&&heap.size())
    {
        int x=heap.top(); heap.pop();  // 取最大偶数
        x/=2;  // 减半
        if(x%2) ret+=x;  // 减半后为奇数，直接累加
        else heap.push(x);  // 仍为偶数，放回堆待后续可能减半
    }

    // 累加剩余所有偶数
    while(heap.size())
    {
        ret+=heap.top();
        heap.pop();
    }

    cout<<ret;  // 输出总和
    return 0;
}

七.习题：最小函数值

1.题目

最小函数值

2.解题思路

这道题的核心是从n个单调递增的二次函数中，高效找出前m个最小的函数值。

注：暴力解法会超时不可取

2.1 问题分析（结合图片示例）

题目给出n个二次函数 ( F_i(x) = A_i x^2 + B_i x + C_i )（( x ) 是正整数），要求找出所有函数值中最小的m个。
关键特性：

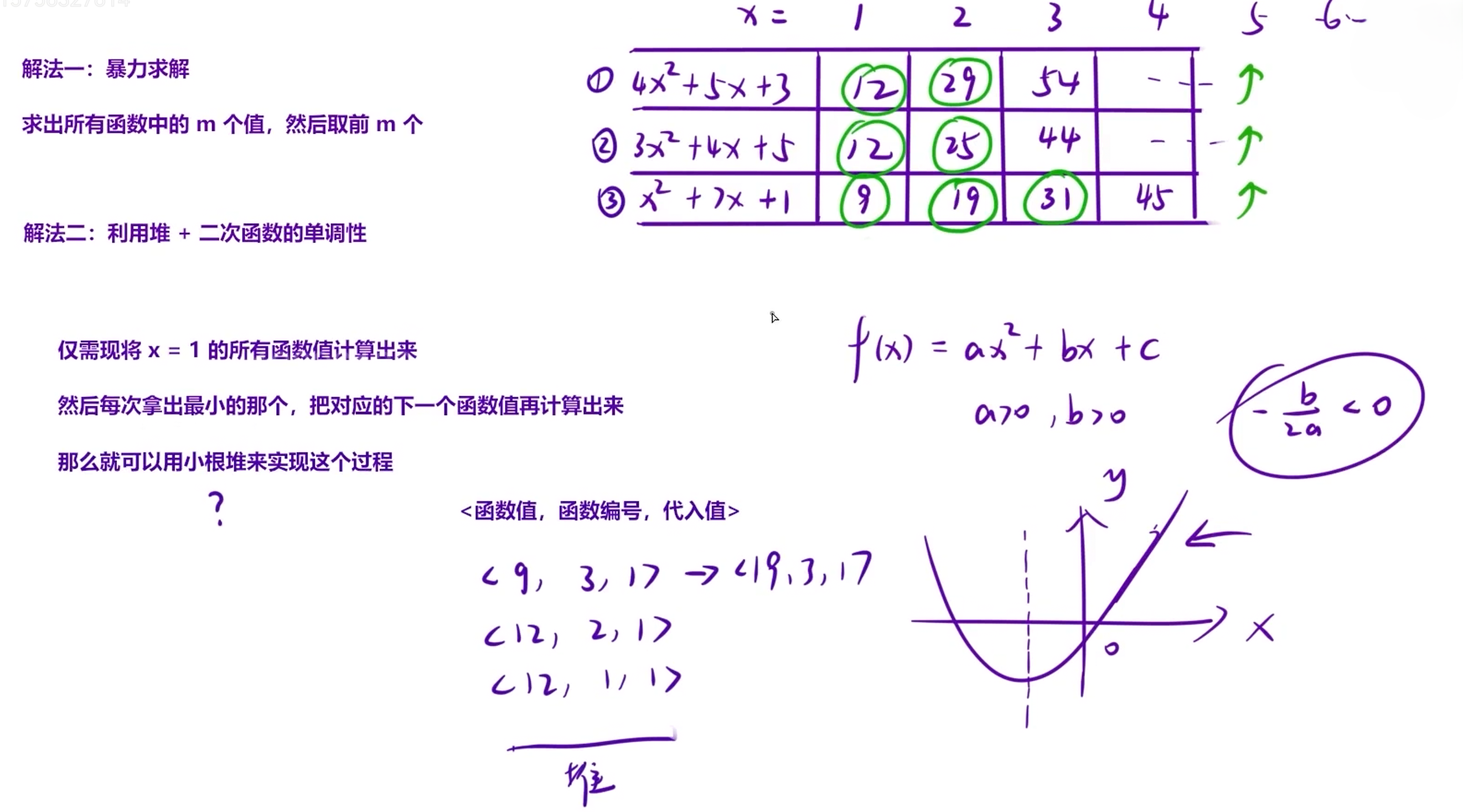
因 ( A_i \geq 1 )，二次函数开口向上，且对称轴 ( x=-b/(2a)< 0 )（结合图片中 ( a>0、b>0 )），因此在 ( x \in \mathbb{N}^ ) 范围内，每个函数的函数值随 ( x ) 增大严格单调递增 （如图片中3个函数的序列：
- 函数①：( 12 , 29, 54 )；
- 函数②：( 12 , 25, 44 )；
- 函数③：( 9 , 19 , 31 )，均是递增序列）。

2.2 核心思路（对应图片"堆+单调性"解法）

每个函数的函数值是一个有序递增序列 ，用小根堆（优先队列） 实现多路归并（图片中"每次拿最小的，补下一个"）：

初始化堆 ：先计算所有函数 ( x=1 ) 时的函数值（图片中 ( x=1 ) 对应的3个值：12、12、9），将这些值（附带"函数编号、当前x值"）加入小根堆（此时堆内元素如图片中的 <9,3,1>、<12,2,1>、<12,1,1>）。
循环取最小值（重复m次） ：
- 取出堆顶（当前全局最小值，如第一次取 <9,3,1>），输出该值；
- 补充该函数的下一个x值 对应的函数值（如函数③的 ( x=2 )，值为19），将 <19,3,2> 加入堆。
循环结束后，输出的m个值就是所有函数值中最小的m个（如图片中前10个值为 9 12 12 19 25 29 31 44 45 54）。

2.3 代码对应逻辑（匹配图片元素）

数据存储 ：用数组 a[N]、b[N]、c[N] 存储函数系数（对应图片中3个函数的 ( A_i、B_i、C_i )）。
堆元素结构 ：struct node 存储 <函数值, 函数编号, 代入值x> （与图片中堆的元素格式一致），通过重载<实现小根堆（让堆顶始终是最小函数值）。
初始化堆：输入每个函数的系数后，计算其 ( x=1 ) 的函数值，加入堆（对应图片中 ( x=1 ) 的3个值入堆）。
取m个最小值 ：每次弹出堆顶（输出），并将该函数的 ( x+1 ) 对应的函数值入堆（如图片中取 <9,3,1> 后，补 <19,3,2>）。

2.4 时间复杂度

初始化堆：( O(n *log n) )（n个 ( x=1 ) 的值入堆，每个入堆操作 ( O(log n) )）。
取m个值：每个值对应"出堆+入堆"，共 ( O(m *log n) )。
整体复杂度 ( O((n+m) *log n) )，能轻松处理 ( n,m <=1e4 ) 的数据规模（如图片中 ( n=3、m=10 ) 的场景）。

3.参考代码

cpp 复制代码

#include <iostream>
#include <queue>//包含优先队列的头文件
using namespace std;

const int N = 1e4 + 10;
typedef long long LL;  // 避免溢出

LL a[N], b[N], c[N];  // 存储n个二次函数系数：a[i]x²+b[i]x+c[i]

// 堆元素结构：函数值f、函数编号num、代入值x
struct node {
    LL f, num, x;
    // 重载<实现小根堆（f大的优先级低）
    bool operator<(const node& t) const {
        return f > t.f;
    }
};

priority_queue<node> heap;  // 小根堆维护候选最小值

// 计算第num个函数在x处的值
LL calc(LL num, LL x) {
    return a[num] * x * x + b[num] * x + c[num];
}

int main() {
    int n, m;  // n：函数个数；m：需输出的最小数个数
    cin >> n >> m;

    // 输入系数，初始化堆（每个函数x=1的值入堆）
    for (int i = 1; i <= n; i++) {
        cin >> a[i] >> b[i] >> c[i];
        heap.push({calc(i, 1), i, 1});
    }

    // 取m个最小值，补充下一个候选值
    while (m--) {
        auto ret = heap.top();
        heap.pop();
        cout << ret.f << " ";
        // 当前函数x+1的值入堆（函数单调递增）
        heap.push({calc(ret.num, ret.x + 1), ret.num, ret.x + 1});
    }

    return 0;
}

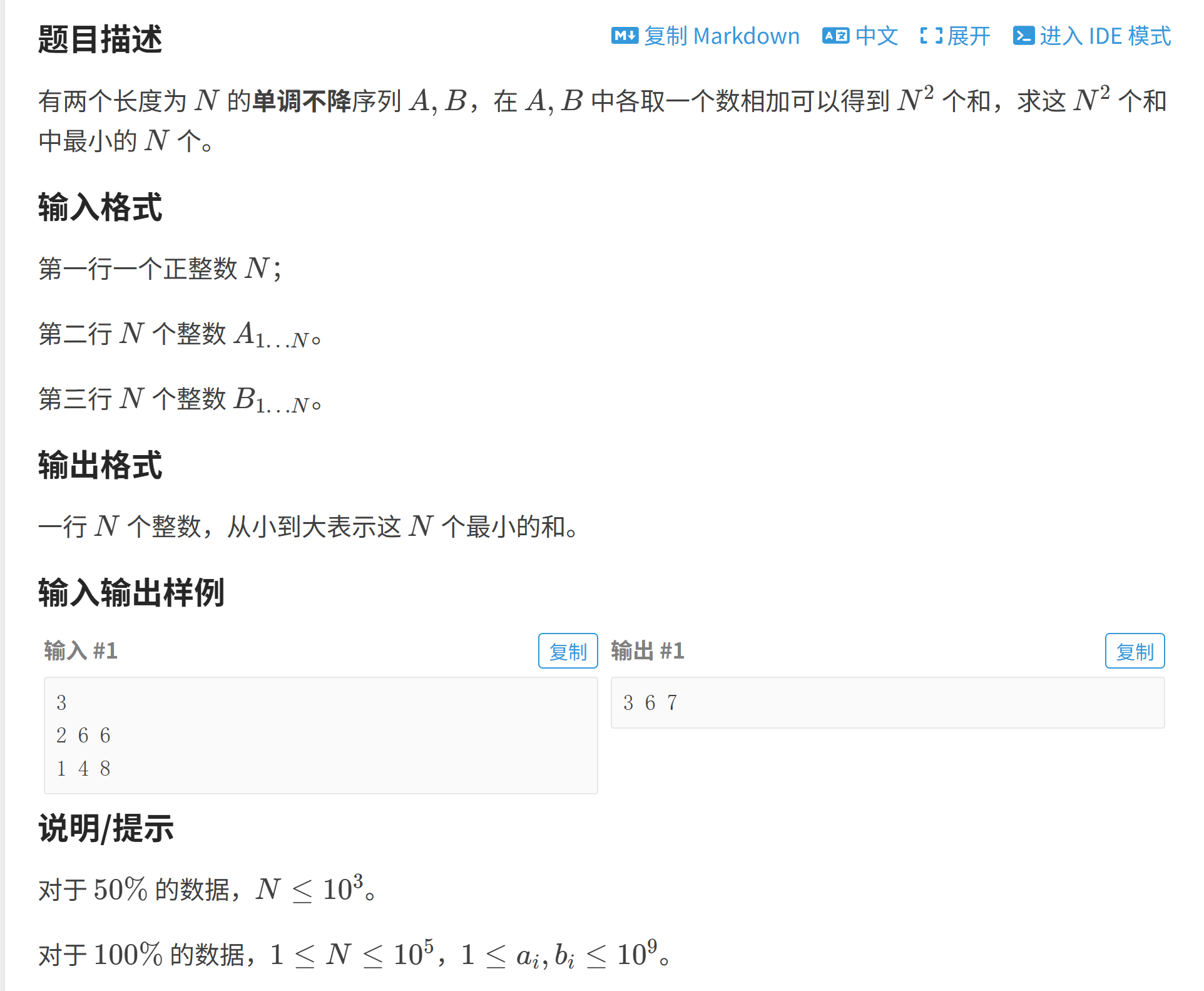
八.习题：序列合并

1.题目

序列合并

2.解题思路

2.1 问题分析

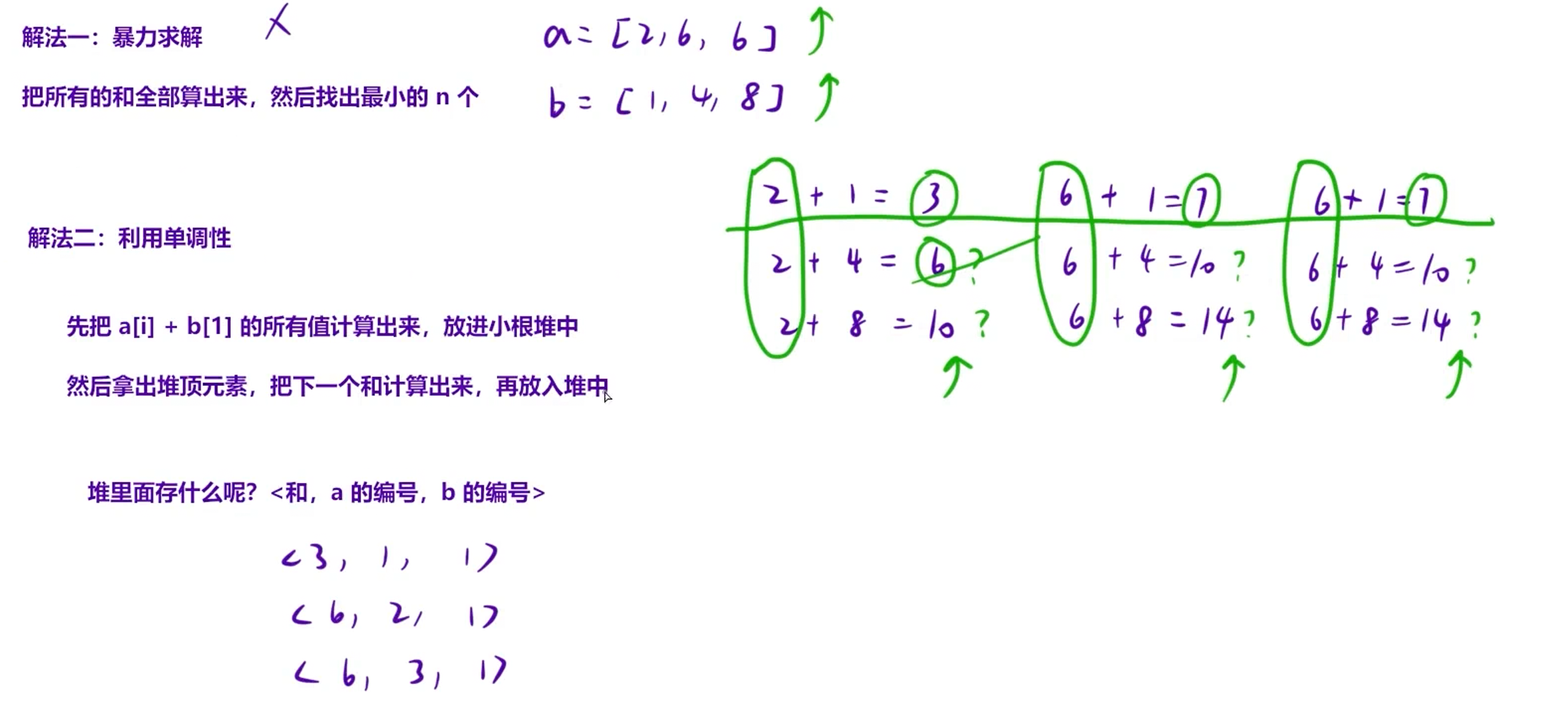
图片中a、b数组是单调非递减的（如a=[2,6,6]、b=[1,4,8]，均递增）；
每个a[i]与b数组的组合（a[i]+b[1], a[i]+b[2], ..., a[i]+b[n]）是一个单调非递减序列 （因为b递增，所以a[i]+b[j]才可能随j增大而增大）。

2.2 核心思路（小根堆实现多路归并）

将每个a[i]对应的序列视为"有序序列"，用小根堆维护这些序列的当前候选最小值，逐步取出前n个最小和：

初始化堆 ：先计算每个a[i]与b[1]的和（每个序列的第一个元素，即当前最小候选），将<和, a的索引, b的索引>存入小根堆（如图片中堆初始元素：<3,1,1>、<6,2,1>、<6,3,1>）。
循环取最小和（n次） ：
- 取出堆顶元素（当前全局最小和，如第一次取<3,1,1>），输出该和；
- 补充该序列的下一个元素 ：若当前b的索引bi未到n，则将a[ai]+b[bi+1]（如<2+4=6,1,2>）存入堆。
循环结束后，输出的n个值就是a[i]+b[j]中最小的n个和。

2.3 代码对应逻辑

数据存储 ：用数组a[N]、b[N]存两个单调递增数组；
堆元素结构 ：struct node存储<和, a的索引, b的索引>，重载<实现小根堆（和越小优先级越高）；
初始化堆 ：将所有a[i]+b[1]的和入堆；
取n个最小和：每次取堆顶并输出，同时补充对应序列的下一个和入堆。

2.4 时间复杂度

初始化堆：O(n log n)（n个元素入堆）；
取n个和：每个和对应"出堆+入堆"，共O(n log n)；
整体复杂度O(n log n)，适配n≤1e5的规模。

3.参考代码

cpp 复制代码

#include<iostream>
#include<queue>
using namespace std;
const int N=1e5+10;
int a[N],b[N];

// 修正1：结构体成员名统一，补充分号，重载<运算符正确
struct node{    
    int sum;  // 存储a[ai] + b[bi]的和
    int ai;   // a数组的索引
    int bi;   // b数组的索引
    // 用sum比较，实现小根堆（sum小的优先级高）
    bool operator<(const node& x) const {
        return sum > x.sum;  // 小根堆：sum大的元素下沉
    }
};  

// 计算a[ai] + b[bi]（ai、bi是1-based索引）
int add(int ai, int bi) {
    return a[ai] + b[bi];
}

priority_queue<node> heap;

int main() {
    int n;
    cin >> n;
    // 输入a数组
    for(int i=1; i<=n; i++) cin >> a[i];
    // 输入b数组
    for(int i=1; i<=n; i++) cin >> b[i];

    // 构造node对象入堆（a[i]搭配b[1]）
    for(int i=1; i<=n; i++) {
        heap.push({add(i, 1), i, 1});  // 大括号构造node：sum、ai、bi
    }

    // 输出前n个最小和
    for(int cnt=1; cnt<=n; cnt++) {
        auto ret = heap.top();
        heap.pop();
        cout << ret.sum << " ";  // 输出当前最小和

        // 若b数组还有下一个元素，将a[ai] + b[bi+1]入堆
        if(ret.bi + 1 <= n) {
            heap.push({add(ret.ai, ret.bi + 1), ret.ai, ret.bi + 1});
        }
    }

    return 0;
}

算法竞赛中的堆

目录

一.堆的概念

二.堆的模拟实现

1.堆的基础存储结构

2.堆的核心操作原理（大顶堆）

2.1 向上调整（up函数）：插入元素后恢复堆性质

2.2 向下调整（down函数）：删除堆顶后恢复堆性质

2.3 插入元素（push函数）

2.4 删除堆顶（pop函数）

2.5 辅助操作（top和size）

3. 测试函数（test01）：堆排序演示

执行过程示例：

4.核心总结

三.priotiy_queue

1. 基本用法

2. 常用操作（O(log n) 时间）

3. 小根堆的实现

4. 竞赛典型应用

5. 注意点

四.习题：【模板】堆

1.题目

五.第 k 小

1.题目

2.解题思路

2.1 问题分析

2.2 核心思路：用大根堆维护"前k小的数"

2.3 代码对应逻辑

2.4 时间复杂度

3.参考代码

六.习题：除2！

1.题目

2.解题思路

2.1 解题思路

2.2 核心亮点

3.参考代码

七.习题：最小函数值

1.题目

2.解题思路

2.1 问题分析（结合图片示例）

2.2 核心思路（对应图片"堆+单调性"解法）

2.3 代码对应逻辑（匹配图片元素）

2.4 时间复杂度

3.参考代码

八.习题：序列合并

1.题目

2.解题思路

2.1 问题分析

2.2 核心思路（小根堆实现多路归并）

2.3 代码对应逻辑

2.4 时间复杂度

3.参考代码