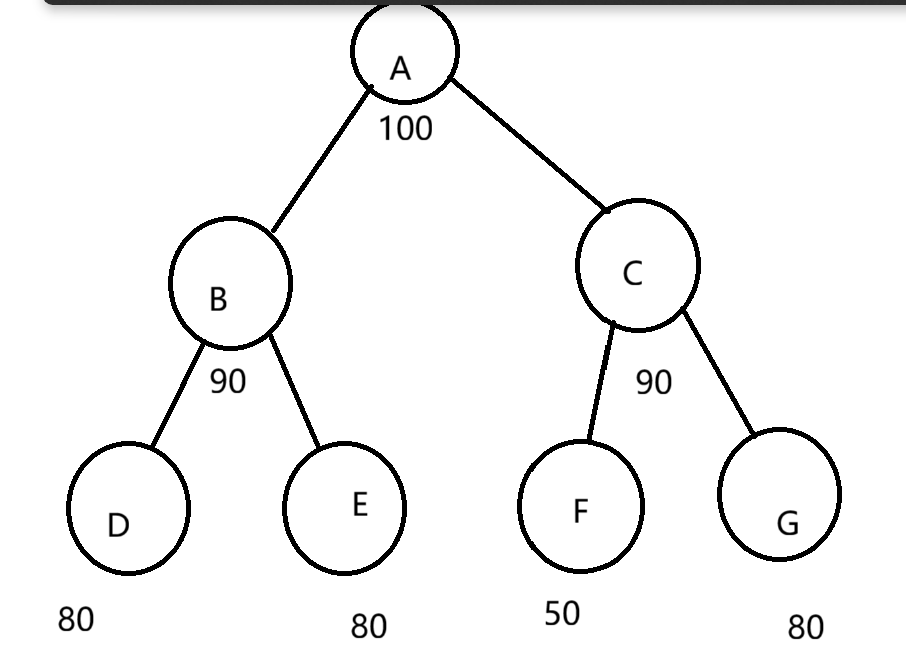
树的概念
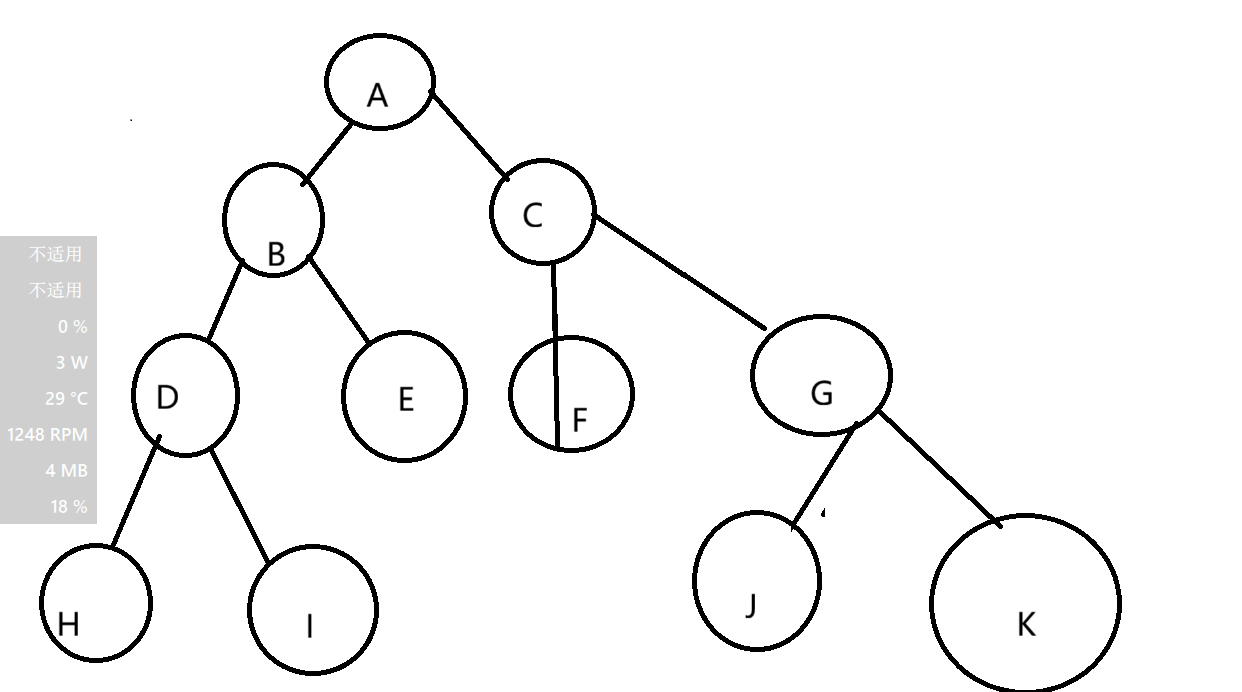
节点的度,一个节点的度是这个节点有多少个直属子节点。
如图中A的度为2.
叶节点||终端节点,是最末端的节点如H,I,E,F,J,K;
非终端节点,除叶节点外的所有节点
双亲节点,如A是父节点,BC是A的子节点,是相对的。
兄弟节点链接在同一双亲节点下的节点如BC
树的度是最大的度
节点的层,从根开始为第一层
树的高度,最大的层
堂兄弟,双亲节点在同一层上如H,JK
子孙,任意节点的子节点,如图中除A以外的节点都是A的子孙
森林,由多棵互不相交的树组成。
任何一棵的树节点不能相交,它是非线性节点。
二叉树
它是一个有限的集合,每个节点只能有最多两个节点向下延申。
满二叉树,每一层都是满的。
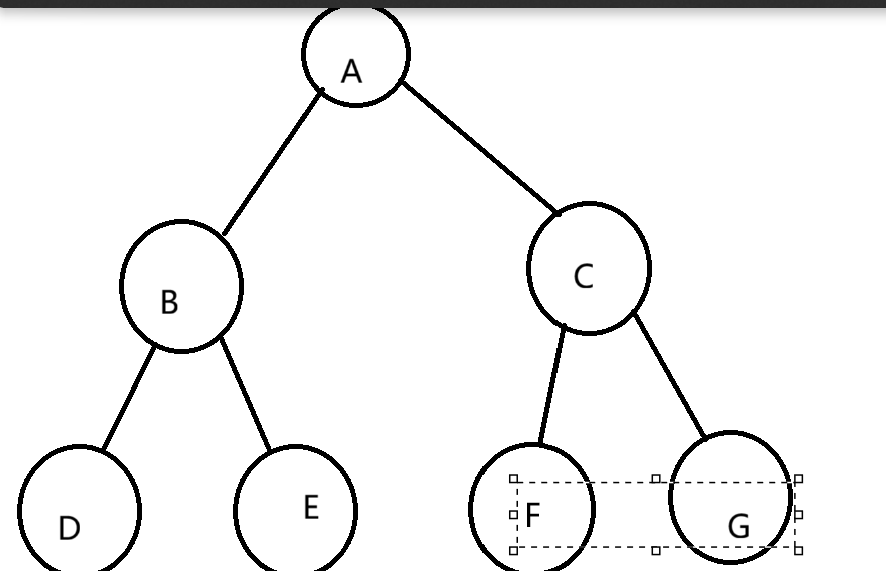
完全二叉树,前n-1层是满的。
大堆和小堆必须是完全二叉树。根可以是最大值和最小值
小堆,每一给父亲的值<=儿子的值
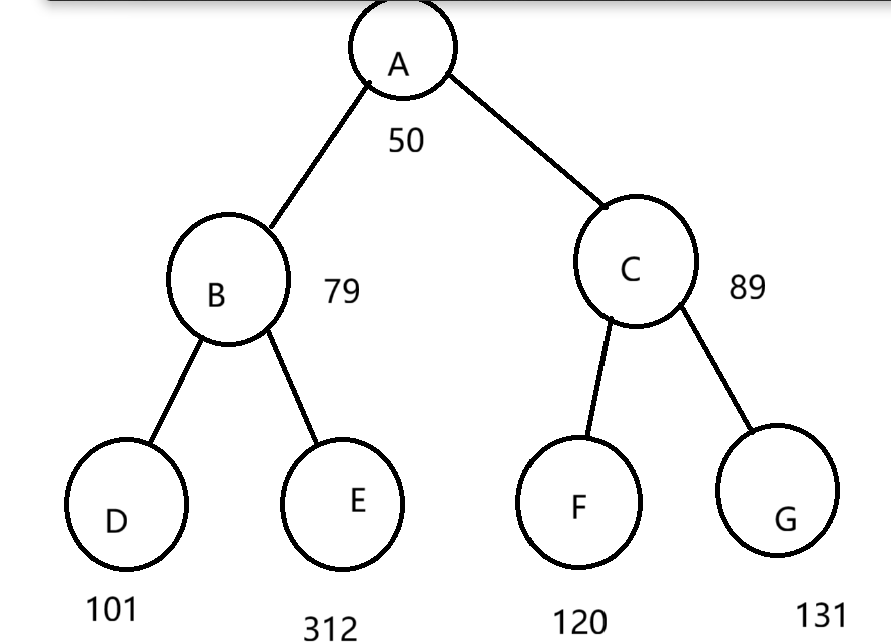
大堆,每一个父亲的值>=儿子的值
小堆二叉树的实现
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>包含的头文件
typedef int fish;
typedef struct tree {
fish* a;//可变数组
int size;//元素个数
int space;//空间大小
}tree;void cs(tree* pst);//初始化
cpp
void cs(tree* pst) {
assert(pst);
pst->a = NULL;
pst->size = pst->space = 0;
}void xh(tree* pst);//销毁
cpp
void xh(tree* pst){
assert(pst);
free(pst->a);
pst->size = 0;
pst->space = 0;
}void push(tree* pst, fish x);//插入
cpp
void push(tree* pst, fish x) {
assert(pst);
if (pst->space == pst->size) {//判断容量够不够
int n = pst->space == 0 ? 4 : pst->space * 2;
fish* cur = (fish*)realloc(pst->a,sizeof(fish) * n);
if (cur == NULL) {
perror("malloc fail");
return;
}
pst->space = n;
pst->a = cur;
}
pst->a[pst->size] = x;//插入数据
just(pst->a, pst->size);//调整为小堆结构
pst->size++;
}void just(fish* a, int chile);
cpp
void just(fish* a, int chile) {//传入数组和最后输入的数据
int parent = (chile - 1) / 2;//上一层的数据
while (chile > 0) {//不是最顶的数据
if (a[chile] < a[parent]) {//如果数据小,向上交换;
sw(&a[chile], &a[parent]);
chile = parent;//更新上一层
parent = (chile - 1) / 2;
}
else {
break;
}
}
}void pop(tree* pst);//删除堆顶;、
cpp
void pop(tree* pst) {
assert(pst);
assert(pst->size > 0);
sw(&(pst->a[pst->size - 1]), &pst->a[0]);//交换头和尾,保持除头以外还是小堆结构
pst->size--;//删除尾
xiatiao(pst->a, pst->size, 0);
}void xiatiao(fish*a,int n,int parent)
cpp
void sw(fish* p1, fish* p2) {
int t = *p1;
*p1 = *p2;
*p2 = t;
}
void xiatiao(fish*a,int n,int parent) {
int child = parent * 2 + 1;//下一层的节点
while (child < n) {//不超过最后一层的数据范围
if ( child+1<n && a[child + 1]<a[child]) {//取较小的节点
++child;
}
if (a[child] < a[parent]) {//比较节点,小的在上
sw(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;//下移一层
}
else {
break;
}
}
}取堆顶和判空
cpp
fish top(tree* pst) {//返回堆顶数据
return pst->a[0];
}
bool emp(tree* pst) {//判空
assert(pst);
if (pst->size == 0)
return true;
return false;
}大堆
改变just的语法
void just(fish* a, int chile);
cpp
void just(fish* a, int chile) {//传入数组和最后输入的数据
int parent = (chile - 1) / 2;//上一层的数据
while (chile > 0) {//不是最顶的数据
if (a[chile] >a[parent]) {//如果数据大,向上交换;
sw(&a[chile], &a[parent]);
chile = parent;//更新上一层
parent = (chile - 1) / 2;
}
else {
break;
}
}
}void pop(tree* pst);//删除堆顶;、
void xiatiao(fish*a,int n,int parent)
cpp
void xiatiao(fish*a,int n,int parent) {
int child = parent * 2 + 1;//下一层的节点
while (child < n) {//不超过最后一层的数据范围
if ( child+1<n && a[child + 1]>a[child]) {da的节点
++child;
}
if (a[child] < a[parent]) {//比较节点,小的在上
sw(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;//下移一层
}
else {
break;
}
}
}其他相同
just函数可以直接把一个数组变成堆并进行堆排序
堆排序的时间复杂度分析
对于满二叉树来说。
设节点个数总数为N,层为H;
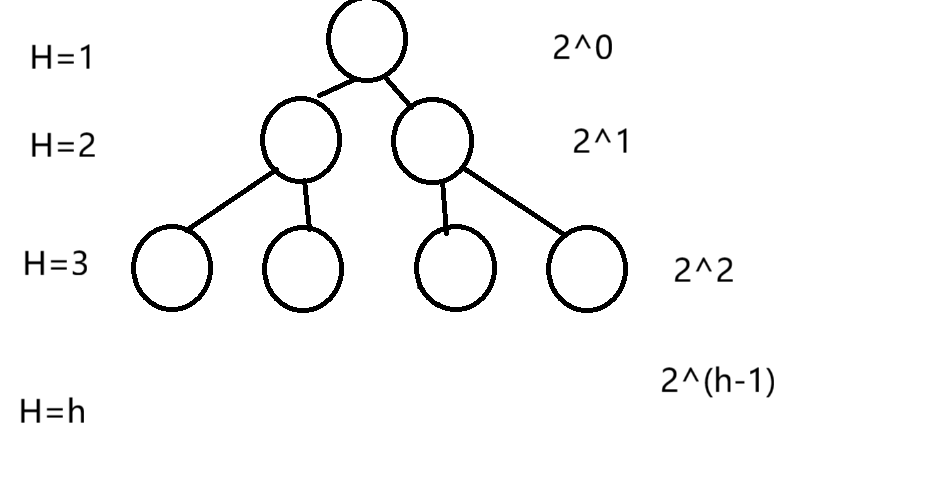
N=2^0+2^1+2^2.....2^(h-1)=2^(h)-1
H=log2(N+1)
向下堆排时间从倒数第二层开始排
T= 2^(h-2)*1 + 2^(h-3)*2......2^1*(h-2)+2^0*(h-1)
2T=2^(h-1)*1+ 2^(h-2)*2 +2^(h-3)*3......2^1*(h-1)
T=2^(h-1)*1+2^(h-2)+2^(h-3)....2^1-h-1;
T=2^(h)-h-1
T=N+1-log2(N+1)-1
O(N);
向下调整是多乘小
向上调整是多乘多
T=2^1*1+2^2*2...2^(h-1)*(h-1)
T=(h−2)⋅2^h+2
T=(log[N+1]-2)*(N+1)+2
O(N*log[N])
堆的使用
取最大的k个数,建一个有k个数小堆,把后进来的数和堆顶进行比较,相当于把k个数中最小的去除,后再拿出一个最小的放在第一位。