IDC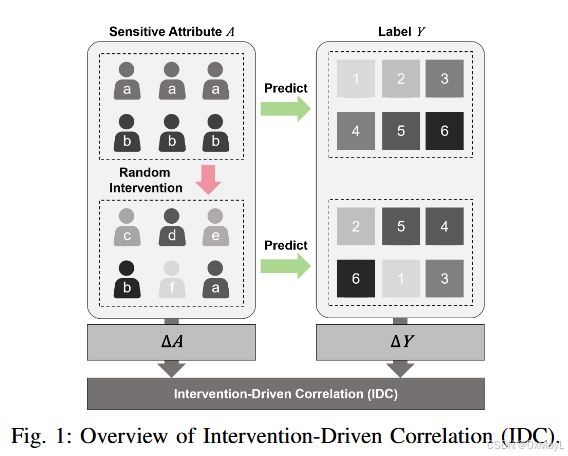
- 核心方法:
remove_edges_sample,通过"删除边"实现干预。这里不是真的删除,而是对于根据父节点的是否被删除,对其后代节点进行干预。 - 就是一个干预do(a)操作。
Utopia Issue
即使生成器生成的数据是公平,但这往往是通过移除中介变量 来实现的,具体来说:
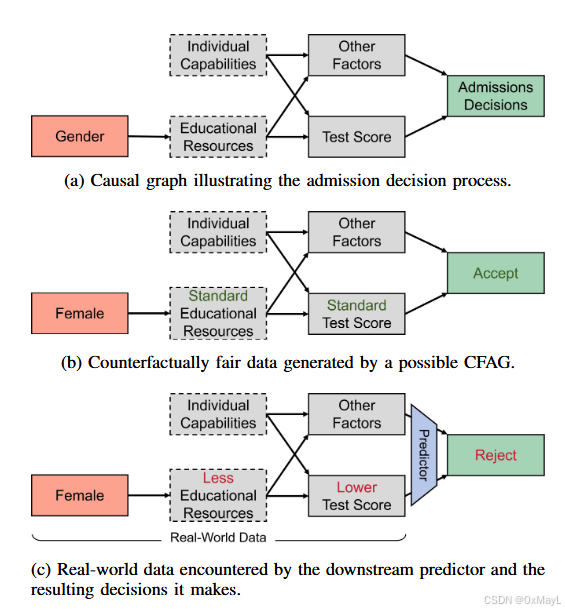
真实的因果图如下:
- 女性-教育资源-分数-是否录取
- 不公平现象因果链:女性的教育资源获得一般较差,因此分数低,被录取概率低
- 生成器的公平因果链:女性-分数-录取概率
- 问题所在:即使生成器生成了公平的数据,但它可能构造了一个与真实数据不一致的路径 ,导致陷入了公平数据的陷阱里。
注意:因果图语言是抽象的,描述上好像是移除了某些边,实际上是生成器之间隐式移除某些边的建模。
例如:性别与教育资源相关,性别生成器和教育资源生成器始终在因果图中,但性别生成器的变化与否已经对教育资源生成器的影响变为0.
原因详细分析
论文指出:
大多数反事实公平数据生成方法通过修改中介变量(mediators)来消除 A→Y 的因果路径,这使得生成数据公平,但会破坏真实世界的因果结构。
然而:
- 在真实世界里,中介变量依然受到敏感属性 A 的影响。
- 下游模型部署到真实环境时,会基于 真实、有偏的中介变量 做决策。
- 因此,即便模型在训练中学到了"公平规则",回到现实后会因中介变量重新引入不公平。
作者通过对比两个结构方程模型(SCM)来解释:
- 真实世界的 SCM :( MrealM_\text{real}Mreal )
- 生成器构造的反事实公平世界 SCM:( M_\\text{cf} )
📌 1. 真实世界中的不公平来源
假设真实世界决定标签的函数为:Y=frealY(pa(Y),UY)Y = f^{Y}_{real}(pa(Y), U_Y)Y=frealY(pa(Y),UY)
不公平意味着:
当我们干预 A 时,Y 会变化:
根本原因:Indirect Discrimination 间接歧视
如果存在中介 (X),使得:Xa≠Xa′X_a \neq X_{a'}Xa=Xa′
即 A 影响 X,而 X 再影响 Y。
这在现实中非常普遍(如:性别→教育资源→考试成绩→录取)。
生成器构造的"公平世界" SCM
为了生成反事实公平数据,生成器构造新的 SCM:Y=fcfY(pa(Y),UY)Y = f^{Y}_{cf}(pa(Y), U_Y)Y=fcfY(pa(Y),UY)
这通常通过 修改中介变量的生成方式 来实现。
真实世界的SCM
下游模型学到的是:fY∗dm=fY∗cff^{Y}*{dm} = f^{Y}*{cf}fY∗dm=fY∗cf
但是部署到真实世界时,模型实际上使用的是:
- 真实世界的中介变量:(XrealX^{real}Xreal)
- 而这些变量仍然满足:干预下,Xa≠Xa′X_a \neq X_{a'}Xa=Xa′
因此,在真实世界的输入下,模型会产生不公平的输出
例子
性别 → 教育资源 → 分数 → 录取结果生成器通过修改分数的产生机制,使其不再受性别的影响:
性别 ×
教育资源 ×
分数 → 录取结果生成的数据确实是公平的。
当模型部署回真实世界时,真实的分数依然受到性别影响:
女性 → 较少资源 → 较低分数 → 被拒绝模型根据真实分数(带偏见)决策,于是:
- 模型在训练数据中公平
- 但在真实环境中重新变得不公平
作者的解决方法
论文提出额外约束(Eq. 30):
fcfX→frealX,∀X∈pa(Y) f^{X}{cf} \to f^{X}{real}, \quad \forall X \in pa(Y) fcfX→frealX,∀X∈pa(Y)
即:
生成器不允许改变中介变量,只能改变 Y 的生成方式。
群体公平指标
DPD:Demographic Parity Difference(人口统计均衡差异)
DPD 衡量不同敏感属性群体(如性别、种族)在**获得正向预测(positive prediction)**方面是否存在差异。
例如:
- 对男性预测收入 >50K 的概率为 30%
- 对女性预测收入 >50K 的概率为 20%
假设敏感属性 ( A ) 具有两个群体(例如 Male / Female):
DPD=∣P(Y^=1∣A=a1)−P(Y^=1∣A=a2)∣ DPD = \left| P(\hat{Y}=1 \mid A=a_1) - P(\hat{Y}=1 \mid A=a_2) \right| DPD= P(Y^=1∣A=a1)−P(Y^=1∣A=a2)
论文中:
- 对数据本身:DPD 衡量 生成的数据是否具有群体公平性
- 对预测器:DPD 衡量 下游模型是否对不同群体给出不同的正预测率
注意:对于连续标签(如 Law School 的成绩),论文采用按中位数二值化后再计算 DPD。
FPRD:False Positive Rate Difference(假阳性率差异)
■ 含义
FPRD 衡量两个群体的假阳性率(False Positive Rate)是否存在差异。
假阳性率定义为:
FPR=P(Y^=1∣Y=0) FPR = P(\hat{Y}=1 \mid Y=0) FPR=P(Y^=1∣Y=0)
也就是:真实标签是 0,但模型预测成 1 的比例。
FPRD 反映的是模型对不同群体 的误判偏差 。
FPRD=∣FPRA=a1−FPRA=a2∣] FPRD = \left| FPR_{A=a_1} - FPR_{A=a_2} \right| ] FPRD=∣FPRA=a1−FPRA=a2∣]
其中,FPRA=a=P(Y\^=1∣Y=0,A=a)FPR_{A=a} = P(\\hat{Y}=1 \\mid Y=0, A=a)FPRA=a=P(Y\^=1∣Y=0,A=a) 注意: * 同样需要把连续标签二值化(论文按 test set 中位数)。 * FPRD 越低 → 模型在不同敏感群体上"误报"的程度越接近 → 更公平。 *** ** * ** ***