从0开始学算法——第三天（数据结构的多样性）

写在开头的话

本文旨在让大家深入理解数据抽象与数据结构类型的概念、特点及应用。通过本文，大家将学习以下内容：

知识点：

（1）数组（2）动态数组（3）链表（4）栈（5）队列（6）堆（7）集合（8）哈希（9）树（10）图

1.数组

数组的定义

数组（Array）是一种线性数据结构，它由一组相同类型的元素按照一定顺序排列而成。每个元素在数组中都有一个唯一的索引，通过索引可以快速访问和操作数组中的元素。

在大多数编程语言中，数组的定义包括以下几个要素：

元素类型：数组中的所有元素必须是相同类型的，可以是整数、浮点数、字符等。
元素个数：数组中元素的个数是固定的，一旦数组被创建，其长度就不能改变。
索引范围：数组的索引通常从 0 开始，依次递增到数组长度减 1。

代码实现

C++ 代码实现

cpp 复制代码

#include <iostream>

int main() {
// 定义一个包含 5 个整数的数组
int numbers[5];

    // 给数组赋值
    for (int i = 0; i < 5; ++i) {
        numbers[i] = i * 10;
    }

    // 访问和输出数组元素
    for (int i = 0; i < 5; ++i) {
        std::cout << "numbers[" << i << "] = " << numbers[i] << std::endl;
    }

    return 0;

}

Java 代码实现

java 复制代码

public class Main {
    public static void main(String[] args) {
        // 定义一个包含5个整数的数组
        int[] numbers = new int[5];

        // 给数组赋值
        for (int i = 0; i < 5; i++) {
            numbers[i] = i * 10;
        }

        // 访问和输出数组元素
        for (int i = 0; i < 5; i++) {
            System.out.println("numbers[" + i + "] = " + numbers[i]);
        }
    }
}

Python 代码实现

python 复制代码

# 定义一个包含5个整数的数组
numbers = [0] * 5

# 给数组赋值

for i in range(5):
    numbers[i] = i * 10

# 访问和输出数组元素

for i in range(5):
    print(f"numbers[{i}] = {numbers[i]}")

运行结果

2.动态数组

动态数组的定义

动态数组（Dynamic Array）是一种可以动态调整大小的数组，它在数组的基础上添加了自动扩容和缩容的功能。动态数组的大小可以根据需要动态增长或减少，而不像静态数组一样在创建时需要指定固定的大小。

动态数组的特点

可以动态地增加或减少元素的数量。
支持随机访问，即可以通过索引直接访问任意位置的元素。
在不需要时可以自动释放不再使用的内存空间。

动态数组的实现通常基于静态数组和指针的组合，当需要增加元素时，会重新分配一块更大的内存空间，将原来的元素复制到新的空间中，然后释放原来的空间。

代码实现示例

动态数组的实现需要考虑数组的动态扩容和缩容功能。以下是一个简单的手动实现动态数组的示例：

C++ 代码实现

cpp 复制代码

#include <iostream>

class DynamicArray {
private:
    int *arr;
    int capacity;
    int size;

public:
    DynamicArray() {
        capacity = 2;
        size = 0;
        arr = new int[capacity];
    }

    void resize(int newCapacity) {
        int *temp = new int[newCapacity];
        for (int i = 0; i < size; i++) {
            temp[i] = arr[i];
        }
        delete[] arr;
        arr = temp;
        capacity = newCapacity;
    }

    void push_back(int element) {
        if (size == capacity) {
            resize(capacity * 2);
        }
        arr[size++] = element;
    }

    void pop_back() {
        if (size > 0) {
            size--;
            if (size <= capacity / 4) {
                resize(capacity / 2);
            }
        }
    }

    int get(int index) {
        if (index < 0 || index >= size) {
            return -1; // 索引越界
        }
        return arr[index];
    }

    int getSize() {
        return size;
    }

    int getCapacity() {
        return capacity;
    }

    ~DynamicArray() {
        delete[] arr;
    }
};

int main() {
    DynamicArray dynamicArray;

    // 向动态数组中添加元素
    for (int i = 0; i < 10; i++) {
        dynamicArray.push_back(i);
    }

    // 输出动态数组的元素
    for (int i = 0; i < dynamicArray.getSize(); i++) {
        std::cout << dynamicArray.get(i) << " ";
    }
    std::cout << std::endl;

    // 输出动态数组的容量
    std::cout << "Capacity: " << dynamicArray.getCapacity() << std::endl;

    // 删除最后一个元素
    dynamicArray.pop_back();

    // 输出删除后的动态数组元素和容量
    for (int i = 0; i < dynamicArray.getSize(); i++) {
        std::cout << dynamicArray.get(i) << " ";
    }
    std::cout << std::endl;
    std::cout << "Capacity after pop: " << dynamicArray.getCapacity() << std::endl;

    return 0;
}

Java 代码实现

java 复制代码

public class DynamicArray {
    private int[] arr;
    private int capacity;
    private int size;

    public DynamicArray() {
        capacity = 2;
        size = 0;
        arr = new int[capacity];
    }

    private void resize(int newCapacity) {
        int[] temp = new int[newCapacity];
        for (int i = 0; i < size; i++) {
            temp[i] = arr[i];
        }
        arr = temp;
        capacity = newCapacity;
    }

    public void push_back(int element) {
        if (size == capacity) {
            resize(capacity * 2);
        }
        arr[size++] = element;
    }

    public void pop_back() {
        if (size > 0) {
            size--;
            if (size <= capacity / 4) {
                resize(capacity / 2);
            }
        }
    }

    public int get(int index) {
        if (index < 0 || index >= size) {
            return -1; // 索引越界
        }
        return arr[index];
    }

    public int getSize() {
        return size;
    }

    public int getCapacity() {
        return capacity;
    }

    public static void main(String[] args) {
        DynamicArray dynamicArray = new DynamicArray();

        // 向动态数组中添加元素
        for (int i = 0; i < 10; i++) {
            dynamicArray.push_back(i);
        }

        // 输出动态数组的元素
        for (int i = 0; i < dynamicArray.getSize(); i++) {
            System.out.print(dynamicArray.get(i) + " ");
        }
        System.out.println();

        // 输出动态数组的容量
        System.out.println("Capacity: " + dynamicArray.getCapacity());

        // 删除最后一个元素
        dynamicArray.pop_back();

        // 输出删除后的动态数组元素和容量
        for (int i = 0; i < dynamicArray.getSize(); i++) {
            System.out.print(dynamicArray.get(i) + " ");
        }
        System.out.println();
        System.out.println("Capacity after pop: " + dynamicArray.getCapacity());
    }

}

Python 代码实现

python 复制代码

class DynamicArray:
    def __init__(self):
        self.capacity = 2
        self.size = 0
        self.arr = [0] * self.capacity

    def resize(self, new_capacity):
        temp = [0

] * new_capacity
        for i in range(self.size):
            temp[i] = self.arr[i]
        self.arr = temp
        self.capacity = new_capacity

    def push_back(self, element):
        if self.size == self.capacity:
            self.resize(self.capacity * 2)
        self.arr[self.size] = element
        self.size += 1

    def pop_back(self):
        if self.size > 0:
            self.size -= 1
            if self.size <= self.capacity // 4:
                self.resize(self.capacity // 2)

    def get(self, index):
        if index < 0 or index >= self.size:
            return -1  # 索引越界
        return self.arr[index]

    def get_size(self):
        return self.size

    def get_capacity(self):
        return self.capacity


# 创建动态数组对象
dynamic_array = DynamicArray()

# 向动态数组中添加元素
for i in range(10):
    dynamic_array.push_back(i)

# 输出动态数组的元素
for i in range(dynamic_array.get_size()):
    print(dynamic_array.get(i), end=" ")
print()

# 输出动态数组的容量
print("Capacity:", dynamic_array.get_capacity())

# 删除最后一个元素
dynamic_array.pop_back()

# 输出删除后的动态数组元素和容量
for i in range(dynamic_array.get_size()):
    print(dynamic_array.get(i), end=" ")
print()
print("Capacity after pop:", dynamic_array.get_capacity())

以上是手动实现动态数组的示例代码，展示了如何创建、添加元素、删除元素和获取元素等操作。这种动态数组的实现方式可以根据需要动态地调整数组的大小，提高了灵活性和效率。

运行结果

3.链表

链表的定义

链表（Linked List）是一种线性数据结构，它由一系列节点（Node）组成，每个节点包含两部分：数据域（存储数据的部分）和指针域（指向下一个节点的指针）。链表中的节点按顺序连接在一起，通过指针将它们串联起来。

代码实现

链表示例代码如下：

C++ 代码实现

cpp 复制代码

#include <iostream>

// 链表节点定义
struct Node {
int data;
Node* next;
Node(int val) : data(val), next(nullptr) {}
};

int main() {
// 创建链表节点
Node* head = new Node(1);
head->next = new Node(2);
head->next->next = new Node(3);

    // 遍历链表并输出节点值
    Node* current = head;
    while (current != nullptr) {
        std::cout << current->data << " ";
        current = current->next;
    }
    std::cout << std::endl;

    return 0;

}

Java 代码实现

java 复制代码

public class Main {
    static class Node {
        int data;
        Node next;
        Node(int val) {
            data = val;
            next = null;
        }
    }

    public static void main(String[] args) {
        // 创建链表节点
        Node head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);

        // 遍历链表并输出节点值
        Node current = head;
        while (current != null) {
            System.out.print(current.data + " ");
            current = current.next;
        }
        System.out.println();
    }
}

Python 代码实现

python 复制代码

# 链表节点定义
class Node:
    def __init__(self, val):
        self.data = val
        self.next = None

# 创建链表节点

head = Node(1)
head.next = Node(2)
head.next.next = Node(3)

# 遍历链表并输出节点值

current = head
while current is not None:
print(current.data, end=" ")
current = current.next
print()

以上是单向链表的定义和在 C++、Java 和 Python 中的示例代码。链表的定义允许我们动态地添加或删除节点，提供了一种灵活的数据存储方式。

运行结果

图示

在这里我们使用的是简单的尾插法，尾插法的原理如下：

尾插法图示

4.栈

栈的定义

栈（Stack）是一种线性数据结构，它遵循后进先出（Last In First Out，LIFO）的原则。栈可以看作是一堆盘子，最先放入的盘子在底部，最后放入的盘子在顶部，取盘子时也是从顶部开始取。

图示

栈存放数据的图示

栈的基本操作

压入（Push）：向栈顶添加一个元素。
弹出（Pop）：从栈顶移除一个元素。
查看栈顶元素（Top）：获取栈顶元素的值，但不删除它。
判断栈是否为空：检查栈是否为空。

栈通常用于需要后进先出顺序的场景，比如函数调用、表达式求值、括号匹配等。

栈的应用举例

在函数调用过程中，用栈来保存函数调用的上下文信息。
实现浏览器的前进和后退功能。
括号匹配问题，如判断括号是否匹配合法。
表达式求值，后缀表达式的计算。

代码实现示例

以下是栈的定义和基本操作的示例代码，展示了如何使用栈来压入、弹出元素以及查看栈顶元素。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <stack>

int main() {
    std::stack<int> myStack;

    // 压入元素到栈中
    myStack.push(10);
    myStack.push(20);
    myStack.push(30);

    // 查看栈顶元素
    std::cout << "Top element: " << myStack.top() << std::endl;

    // 弹出栈顶元素
    myStack.pop();

    // 再次查看栈顶元素
    std::cout << "Top element after pop: " << myStack.top() << std::endl;

    return 0;
}

Java 代码实现

java 复制代码

import java.util.Stack;

public class Main {
public static void main(String[] args) {
Stack<Integer> myStack = new Stack<>();

        // 压入元素到栈中
        myStack.push(10);
        myStack.push(20);
        myStack.push(30);

        // 查看栈顶元素
        System.out.println("Top element: " + myStack.peek());

        // 弹出栈顶元素
        myStack.pop();

        // 再次查看栈顶元素
        System.out.println("Top element after pop: " + myStack.peek());
    }

}

Python 代码实现

python 复制代码

# 使用列表模拟栈
my_stack = []

# 压入元素到栈中
my_stack.append(10)
my_stack.append(20)
my_stack.append(30)

# 查看栈顶元素
print("Top element:", my_stack[-1])

# 弹出栈顶元素
my_stack.pop()

# 再次查看栈顶元素
print("Top element after pop:", my_stack[-1])

运行结果

5.队列

队列的定义

队列（Queue）是一种线性数据结构，它遵循先进先出（First In First Out，FIFO）的原则。队列可以看作是一排排队的人，最先进入队列的人最先被服务或者出队。

图示

队列的元素进出

队列的基本操作

入队（Enqueue）：向队尾添加一个元素。
出队（Dequeue）：从队头移除一个元素。
查看队头元素（Front）：获取队头元素的值，但不删除它。
查看队尾元素（Rear）：获取队尾元素的值，但不删除它。
判断队列是否为空：检查队列是否为空。

队列通常用于需要先进先出顺序的场景，比如任务调度、消息队列、广度优先搜索等。

队列的应用举例

网络数据包的传输。
打印任务的排队。
操作系统的进程调度。
宽度优先搜索算法的实现。

代码实现示例

以下是队列的定义和基本操作的示例代码，展示了如何使用队列来入队、出队以及查看队头和队尾元素。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <queue>

int main() {
std::queue<int> myQueue;

    // 入队操作
    myQueue.push(10);
    myQueue.push(20);
    myQueue.push(30);

    // 查看队头元素
    std::cout << "Front element: " << myQueue.front() << std::endl;

    // 出队操作
    myQueue.pop();

    // 再次查看队头元素
    std::cout << "Front element after dequeue: " << myQueue.front() << std::endl;

    // 查看队尾元素
    std::cout << "Rear element: " << myQueue.back() << std::endl;

    return 0;

}

Java 代码实现

java 复制代码

import java.util.LinkedList;
import java.util.Queue;

public class Main {
    public static void main(String[] args) {
        Queue<Integer> myQueue = new LinkedList<>();

        // 入队操作
        myQueue.offer(10);
        myQueue.offer(20);
        myQueue.offer(30);

        // 查看队头元素
        System.out.println("Front element: " + myQueue.peek());

        // 出队操作
        myQueue.poll();

        // 再次查看队头元素
        System.out.println("Front element after dequeue: " + myQueue.peek());

        // 查看队尾元素
        System.out.println("Rear element: " + ((LinkedList<Integer>) myQueue).getLast());
    }
}

Python 代码实现

python 复制代码

from collections import deque

# 创建队列对象

my_queue = deque()

# 入队操作

my_queue.append(10)
my_queue.append(20)
my_queue.append(30)

# 查看队头元素

print("Front element:", my_queue[0])

# 出队操作

my_queue.popleft()

# 再次查看队头元素

print("Front element after dequeue:", my_queue[0])

# 查看队尾元素

print("Rear element:", my_queue[-1])

运行结果

6.堆

堆的定义

堆（Heap）是一种特殊的树形数据结构，它通常是一个完全二叉树。堆分为大根堆（Max Heap）和小根堆（Min Heap）两种类型。

大根堆（Max Heap）：在一个大根堆中，任意节点的值都大于或等于其子节点的值。
小根堆（Min Heap）：在一个小根堆中，任意节点的值都小于或等于其子节点的值。

图示

堆排序的运行图

堆的特点

堆是一棵完全二叉树，通常使用数组来表示。
在大根堆中，根节点是堆中的最大元素；在小根堆中，根节点是堆中的最小元素。
堆中的每个节点的值都必须满足堆的性质。

堆的基本操作

插入元素：将一个新的元素插入到堆中。
删除根节点：删除堆中的根节点，并重新调整堆结构使其满足堆的性质。
获取堆顶元素：获取堆中的根节点值，但不删除它。
堆化（Heapify）：将一个无序的数组转换为堆。

堆通常用于实现优先队列、堆排序、求解Top K 问题等。

堆的应用

优先队列的实现。
堆排序算法。
实现求解Top K 问题，如查找数组中最大的K个元素。
Dijkstra算法和Prim算法等图算法的实现。

代码实现示例

以下是堆的定义和基本操作的示例代码，展示了如何使用堆来获取堆顶元素、删除堆顶元素等操作。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> maxHeap = {10, 20, 15, 40, 50, 100, 25};

    // 将 vector 转换为大根堆
    std::make_heap(maxHeap.begin(), maxHeap.end());

    // 获取堆顶元素（最大值）
    std::cout << "Root element (Max): " << maxHeap.front() << std::endl;

    // 删除堆顶元素
    std::pop_heap(maxHeap.begin(), maxHeap.end());
    maxHeap.pop_back();

    // 再次获取堆顶元素
    std::cout << "Root element after deletion: " << maxHeap.front() << std::endl;

    return 0;
}

Java 代码实现

java 复制代码

import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class Main {
public static void main(String[] args) {
List<Integer> maxHeap = Arrays.asList(10, 20, 15, 40, 50, 100, 25);

        // 将 List 转换为大根堆
        Collections.sort(maxHeap, Collections.reverseOrder());

        // 获取堆顶元素（最大值）
        System.out.println("Root element (Max): " + maxHeap.get(0));

        // 删除堆顶元素
        maxHeap.remove(0);

        // 再次获取堆顶元素
        System.out.println("Root element after deletion: " + maxHeap.get(0));
    }

}

Python 代码实现

python 复制代码

import heapq

# 创建大根堆
max_heap = [10, 20, 15, 40, 50, 100, 25]

# 将列表转换为大根堆
heapq._heapify_max(max_heap)

# 获取堆顶元素（最大值）
print("Root element (Max):", max_heap[0])

# 删除堆顶元素
heapq._heappop_max(max_heap)

# 再次获取堆顶元素
print("Root element after deletion:", max_heap[0])

运行结果

7.集合

集合的定义

集合（Set）是一种不允许包含重复元素的数据结构，它主要用于存储元素的无序集合。在集合中，每个元素都是唯一的，不存在重复的元素。

集合的特点

集合中的元素无序存储，没有索引。
每个元素在集合中都是唯一的，不允许重复。
集合通常用于存储元素的查找和去重。

集合的基本操作

添加元素：向集合中添加一个新的元素。
删除元素：从集合中删除指定的元素。
查找元素：检查集合中是否包含某个元素。
获取集合大小：获取集合中元素的个数。

集合可以用于解决许多去重和查找元素的问题。

集合的应用举例

去除列表中的重复元素。
查找两个数组的交集、并集、差集等操作。
检查网页中的关键词是否重复出现。

代码实现示例

以下是集合的定义和基本操作的示例代码，展示了如何使用集合来添加元素、删除元素、查找元素以及获取集合大小等操作。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <set>

int main() {
std::set<int> mySet;

    // 添加元素到集合中
    mySet.insert(10);
    mySet.insert(20);
    mySet.insert(30);
    mySet.insert(20);  // 重复元素不会被添加

    // 删除元素
    mySet.erase(20);

    // 查找元素
    if (mySet.find(30) != mySet.end()) {
        std::cout << "Element 30 found in set." << std::endl;
    } else {
        std::cout << "Element 30 not found in set." << std::endl;
    }

    // 获取集合大小
    std::cout << "Size of set: " << mySet.size() << std::endl;

    return 0;

}

Java 代码实现

java 复制代码

import java.util.HashSet;
import java.util.Set;

public class Main {
    public static void main(String[] args) {
        Set<Integer> mySet = new HashSet<>();

        // 添加元素到集合中
        mySet.add(10);
        mySet.add(20);
        mySet.add(30);
        mySet.add(20);  // 重复元素不会被添加

        // 删除元素
        mySet.remove(20);

        // 查找元素
        if (mySet.contains(30)) {
            System.out.println("Element 30 found in set.");
        } else {
            System.out.println("Element 30 not found in set.");
        }

        // 获取集合大小
        System.out.println("Size of set: " + mySet.size());
    }
}

Python 代码实现

python 复制代码

my_set = set()

# 添加元素到集合中

my_set.add(10)
my_set.add(20)
my_set.add(30)
my_set.add(20) # 重复元素不会被添加

# 删除元素

my_set.remove(20)

# 查找元素

if 30 in my_set:
print("Element 30 found in set.")
else:
print("Element 30 not found in set.")

# 获取集合大小

print("Size of set:", len(my_set))

运行结果

8.哈希表

哈希表的定义

哈希表（Hash Table）是一种根据键（Key）直接访问值（Value）的数据结构，它通过哈希函数（Hash Function）将键映射到存储值的位置上。哈希表通常也被称为哈希映射（Hash Map）或字典（Dictionary）。

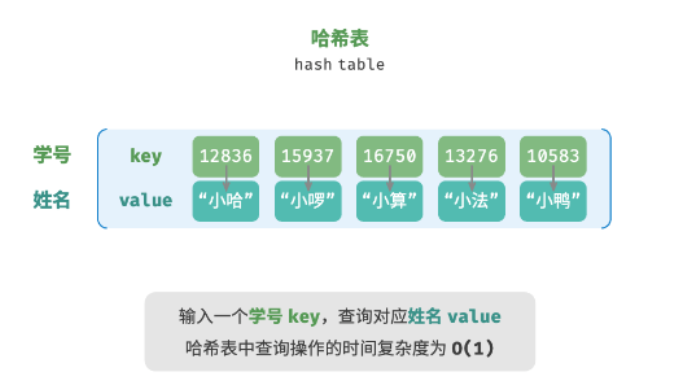
哈希表的特点

使用哈希函数将键转换为哈希码（Hash Code），然后将哈希码映射到特定的存储位置。
哈希表的存储位置通常称为哈希桶（Hash Bucket）或槽（Slot）。
当两个不同的键映射到相同的存储位置时，就会发生哈希冲突（Hash Collision），需要解决冲突。
哈希表的查找、插入和删除操作的时间复杂度通常为 O(1)，在理想情况下可以达到常数时间复杂度。

哈希的实现方法

哈希表（Hash Table）是一种常见的数据结构，用于实现哈希映射（Hash Map）或者哈希集合（Hash Set）。它通过哈希函数将键（Key）映射到存储位置，从而实现快速的插入、删除和查找操作。

哈希表的实现方法主要包括以下几种：

直接寻址表（Direct Addressing Table）

在理想情况下，每个键值对的键都可以作为数组的下标，直接存储在数组中。
这种方法要求键的范围必须是已知的且不会很大，因为数组的大小必须至少为键的范围。
空间利用率高，时间复杂度为 O(1)，但需要大量空间。

拉链法（Chaining）

使用一个数组存储链表或者其他数据结构的头指针，每个头指针指向一个链表。
当发生哈希冲突时，新的键值对会被插入到对应位置的链表中。
空间利用率取决于链表的平均长度，时间复杂度为 O(1+α)，其中 α 为平均链表长度。

开放寻址法（Open Addressing）

所有元素都存储在哈希表的内部数组中。
当发生哈希冲突时，根据特定的探测方法（如线性探测、二次探测、双重散列等）寻找下一个可用的空槽。
这种方法适用于密集存储的情况，空间利用率高，时间复杂度为 O(1)。

二次哈希（Double Hashing）

使用两个哈希函数来解决哈希冲突，计算下一个可用槽的位置。
第一个哈希函数计算初始位置，第二个哈希函数计算步长。
这种方法能够在哈希表填满之前保持高效，但需要选择合适的哈希函数。

哈希表的基本操作

插入键值对：将一个键值对（Key-Value Pair）插入到哈希表中。
删除键值对：从哈希表中删除指定键的键值对。
查找键对应的值：根据给定的键查找对应的值。

哈希表的应用举例

实现字典和关联数组。
数据库索引。
缓存实现。
哈希集合和哈希映射。

代码实现示例

下面是哈希表的定义和基本操作示例代码：

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <unordered_map>

int main() {
    std::unordered_map<std::string, int> myMap;

    // 插入键值对
    myMap["Alice"] = 25;
    myMap["Bob"] = 30;
    myMap["Charlie"] = 35;

    // 查找键对应的值
    std::cout << "Age of Bob: " << myMap["Bob"] << std::endl;

    // 删除键值对
    myMap.erase("Charlie");

    // 检查键是否存在
    if (myMap.find("Alice") != myMap.end()) {
        std::cout << "Alice found in map." << std::endl;
    } else {
        std::cout << "Alice not found in map." << std::endl;
    }

    return 0;
}

Java 代码实现

java 复制代码

import java.util.HashMap;
import java.util.Map;

public class Main {
public static void main(String[] args) {
Map<String, Integer> myMap = new HashMap<>();

        // 插入键值对
        myMap.put("Alice", 25);
        myMap.put("Bob", 30);
        myMap.put("Charlie", 35);

        // 查找键对应的值
        System.out.println("Age of Bob: " + myMap.get("Bob"));

        // 删除键值对
        myMap.remove("Charlie");

        // 检查键是否存在
        if (myMap.containsKey("Alice")) {
            System.out.println("Alice found in map.");
        } else {
            System.out.println("Alice not found in map.");
        }
    }

}

Python 代码实现

python 复制代码

my_dict = {}

# 插入键值对
my_dict["Alice"] = 25
my_dict["Bob"] = 30
my_dict["Charlie"] = 35

# 查找键对应的值
print("Age of Bob:", my_dict["Bob"])

# 删除键值对
del my_dict["Charlie"]

# 检查键是否存在
if "Alice" in my_dict:
    print("Alice found in dictionary.")
else:
    print("Alice not found in dictionary.")

运行结果

9.树

树的定义

树（Tree）是一种层级结构的数据结构，它由节点（Node）和边（Edge）组成。树的最上层节点称为根节点（Root Node），每个节点可以有零个或多个子节点，子节点又可以有自己的子节点，以此类推。树的一个重要特性是没有循环，即不存在任何节点的子孙节点指向其祖先节点。

树的基本概念

根节点（Root）：树的顶层节点，没有父节点。
父节点（Parent）：每个节点除了根节点外，都有一个父节点。
子节点（Children）：一个节点的直接子节点是直接从该节点出发到达的节点。
叶节点（Leaf）：没有子节点的节点称为叶节点。
内部节点（Internal Node）：除了叶节点之外的所有节点都称为内部节点。
路径（Path）：从一个节点到另一个节点的一系列连续的边组成的序列。
高度（Height）：树的高度是从根节点到最远叶节点的最长路径的长度。
深度（Depth）：一个节点到根节点的唯一路径的长度。

树可以用来模拟许多实际情况，比如文件系统的目录结构、组织结构、家谱等。树结构的使用可以有效地表示和处理层次关系的数据。

树的示意图

在上面的示意图中，节点 A 是根节点，它有三个子节点 B、C、D，B 节点又有两个子节点 E、F，而 D 节点有一个子节点 G。

树是许多重要数据结构的基础，如二叉树、平衡树、堆等。它在计算机科学中有着广泛的应用。

代码实现示例

以下是树的定义和创建的示例代码，展示了如何使用 C++、Java 和 Python 来定义和构建树结构。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>

struct TreeNode {
    int val;
    std::vector<TreeNode*> children;
    TreeNode(int x) : val(x) {}
};

int main() {
    // 创建根节点 A
    TreeNode* root = new TreeNode(1);

    // 创建子节点 B、C、D
    TreeNode* nodeB = new TreeNode(2);
    TreeNode* nodeC = new TreeNode(3);
    TreeNode* nodeD = new TreeNode(4);

    // 将 B、C、D 作为 A 的子节点
    root->children.push_back(nodeB);
    root->children.push_back(nodeC);
    root->children.push_back(nodeD);

    return 0;
}

Java 代码实现

java 复制代码

import java.util.ArrayList;
import java.util.List;

class TreeNode {
    int val;
    List<TreeNode> children;
    TreeNode(int x) {
        val = x;
        children = new ArrayList<>();
    }
}

public class Main {
    public static void main(String[] args) {
        // 创建根节点 A
        TreeNode root = new TreeNode(1);

        // 创建子节点 B、C、D
        TreeNode nodeB = new TreeNode(2);
        TreeNode nodeC = new TreeNode(3);
        TreeNode nodeD = new TreeNode(4);

        // 将 B、C、D 作为 A 的子节点
        root.children.add(nodeB);
        root.children.add(nodeC);
        root.children.add(nodeD);
    }
}

Python 代码实现

python 复制代码

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.children = []

# 创建根节点 A
root = TreeNode(1)

# 创建子节点 B、C、D
nodeB = TreeNode(2)
nodeC = TreeNode(3)
nodeD = TreeNode(4)

# 将 B、C、D 作为 A 的子节点
root.children.append(nodeB)
root.children.append(nodeC)
root.children.append(nodeD)

10.图

图的定义

图是由节点（或顶点）和连接这些节点的边组成的一种抽象数据结构。在图中，节点表示实体，边表示节点之间的关系。图可以用来描述各种实际问题，例如网络连接、社交关系、道路系统等。

图的分类

图可以分为有向图和无向图两种类型：

（1）有向图（Directed Graph）：图中的边具有方向，从一个节点指向另一个节点。表示为 (u, v)，表示从节点 u 到节点 v 存在一条有向边。

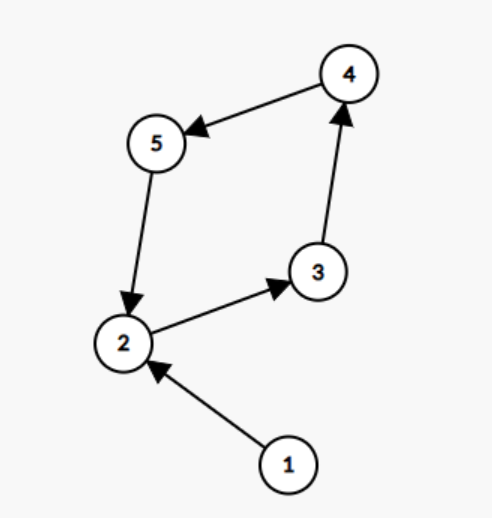
（2）无向图（Undirected Graph）：图中的边没有方向，连接两个节点的边是双向的。表示为 {u, v}，表示节点 u 和节点 v 之间有一条无向边。

图的元素

图中可能包含以下元素：

节点（或顶点）：图中的实体，可以是任何对象或数据。
边（或弧）：连接节点的线条，表示节点之间的关系。
权重（Weight）：边可以带有权重，表示节点之间的距离、成本或其他属性。
邻接点（Adjacent Vertices）：与某个节点直接相连的节点。
路径（Path）：连接图中的节点的边的序列。

图的定义方式

有向图 G = (V, E)，其中 V 是节点的集合，E 是边的集合，每条边是一个有序对 (u, v)，u 和 v 分别是图中的节点。
无向图 G = (V, E)，其中 V 是节点的集合，E 是边的集合，每条边是一个无序对 {u, v}，u 和 v 分别是图中的节点。

这种抽象的数据结构非常适用于解决许多现实世界中的问题，如社交网络分析、路由算法、图像处理等。

邻接表和邻接矩阵

邻接表和邻接矩阵是两种常用的图的表示方法，它们在存储图结构时具有不同的特点和适用场景。

邻接表

邻接表是一种基于链表的图表示方法。对于图中的每个节点，邻接表存储其所有相邻节点的列表。每个节点都有一个与之对应的链表，链表中的每个节点表示与该节点相邻的另一个节点。

优点

适用于稀疏图（边数相对节点数较少）。
占用的空间较小，仅存储图中存在的边。
方便查找某个节点的邻接节点。

缺点

查找两个节点之间是否存在边需要遍历链表，时间复杂度较高。

邻接矩阵

邻接矩阵是一种基于二维数组的图表示方法。对于图中的每一对节点，邻接矩阵中的一个元素表示它们之间是否存在边。如果两个节点之间存在边，则相应的元素为 1 或表示边的权重；如果不存在边，则为 0 或表示不存在的值。

优点

适用于稠密图（边数接近节点数的平方）。
方便查找两个节点之间是否存在边，时间复杂度为 O(1)。

缺点

占用的空间较大，当图规模较大时，可能会占用过多的内存空间。
不太适用于稀疏图，因为大部分元素都是 0，造成空间浪费。

邻接表和邻接矩阵各有其优势和局限性，在选择图的表示方法时，需要根据具体的应用场景和需求进行权衡和选择。

从0开始学算法——第三天（数据结构的多样性）

写在开头的话

1.数组

数组的定义

代码实现

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

2.动态数组

动态数组的定义

动态数组的特点

代码实现示例

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

3.链表

链表的定义

分类

单向链表

双向链表

循环链表

代码实现

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

图示

4.栈

栈的定义

图示

栈的基本操作

栈的应用举例

代码实现示例

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

5.队列

队列的定义

图示

队列的基本操作

队列的应用举例

代码实现示例

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

6.堆

堆的定义

图示

堆的特点

堆的基本操作

堆的应用

代码实现示例

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

7.集合

集合的定义

集合的特点

集合的基本操作

集合的应用举例

代码实现示例

C++ 代码实现

Java 代码实现

Python 代码实现

运行结果

8.哈希表

哈希表的定义

哈希表的特点

哈希的实现方法

直接寻址表（Direct Addressing Table）

拉链法（Chaining）

开放寻址法（Open Addressing）

二次哈希（Double Hashing）

哈希表的基本操作

哈希表的应用举例