MATLAB 探索轴承动力学：从故障建模到数据模拟

MATLAB轴承动力学代码（正常、外圈故障、内圈故障、滚动体故障），根据滚动轴承故障机理建模（含数学方程建立和公式推导）并在MATLAB中采用ODE45进行数值计算。可模拟不同轴承故障类型，输出时域波形、相图、轴心轨迹、频谱图、包络谱图、滚道接触力，根据模拟数据后续可在此基础上继续开展故障诊断和剩余寿命预测。

在机械工程领域，轴承的健康状态监测至关重要。通过 MATLAB 对轴承动力学进行模拟，我们能够深入了解不同故障类型下轴承的运行特性，为后续的故障诊断和剩余寿命预测打下基础。

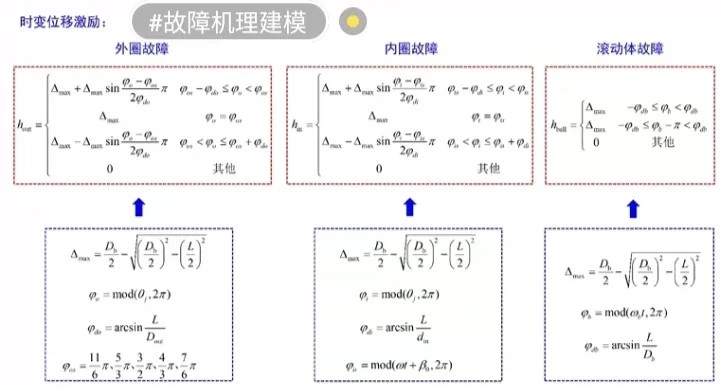
故障机理建模

数学方程建立

轴承的动力学模型较为复杂，以单自由度的轴承故障模型为例，其运动方程可以表示为：

\[ m\ddot{x} + c\dot{x} + kx = F(t) \]

其中，\( m \) 是质量，\( c \) 是阻尼系数，\( k \) 是刚度系数，\( x \) 是位移，\( F(t) \) 是外部激励力。对于不同的故障类型，\( F(t) \) 的形式会有所不同。

公式推导

以滚动体故障为例，当滚动体出现故障时，会产生冲击激励。假设故障点通过载荷区时产生一个脉冲力，这个脉冲力可以用狄拉克函数来近似表示：

\[ F(t) = A\sum_{n = -\infty}^{\infty} \delta(t - nT - \tau) \]

其中，\( A \) 是脉冲幅值，\( T \) 是滚动体通过频率的倒数，\( \tau \) 是故障发生的初始相位。

MATLAB 数值计算

在 MATLAB 中，我们使用 ode45 函数进行数值计算。以下是一个简单的示例代码：

matlab 复制代码

% 定义参数
m = 1; % 质量
c = 10; % 阻尼系数
k = 100; % 刚度系数

% 定义时间范围
tspan = [0 10];

% 定义初始条件
x0 = [0; 0];

% 定义ODE函数
odefun = @(t, x) [x(2); (-c * x(2) - k * x(1)) / m];

% 求解ODE
[t, x] = ode45(odefun, tspan, x0);

在这段代码中，我们首先定义了系统的参数，如质量、阻尼系数和刚度系数。然后，设定了时间范围 tspan 和初始条件 x0。odefun 函数定义了我们要求解的微分方程，最后使用 ode45 函数求解这个微分方程。

不同故障类型模拟

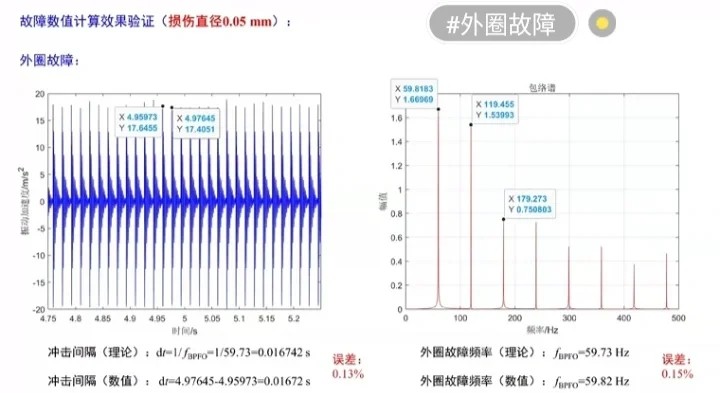
外圈故障

外圈故障时，激励力的频率与外圈故障特征频率相关。我们只需要修改 odefun 函数中的激励力部分，例如：

matlab 复制代码

% 外圈故障特征频率
f_outer =...; % 计算外圈故障特征频率的公式
A_outer = 10; % 脉冲幅值

odefun_outer = @(t, x) [x(2); (-c * x(2) - k * x(1) + A_outer * sin(2 * pi * f_outer * t)) / m];

[t_outer, x_outer] = ode45(odefun_outer, tspan, x0);

内圈故障和滚动体故障

类似地，对于内圈故障和滚动体故障，我们也通过修改激励力的形式来模拟。内圈故障激励力频率与内圈故障特征频率相关，滚动体故障激励力如前文所述用脉冲力模拟。

结果输出

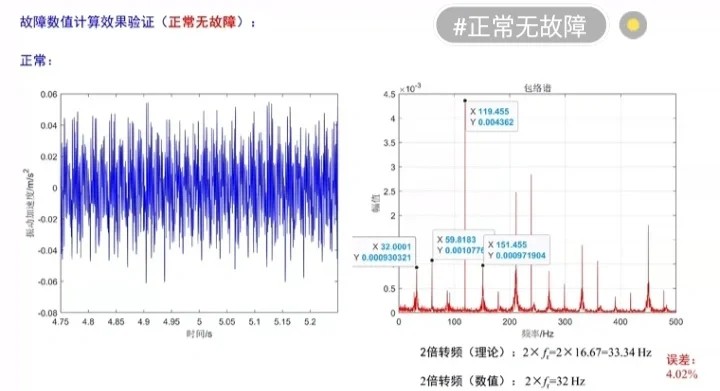
时域波形

绘制位移的时域波形，可以直观地看到系统的振动情况。

matlab 复制代码

figure;
plot(t, x(:, 1));
title('正常状态时域波形');
xlabel('时间 (s)');
ylabel('位移 (m)');

相图

相图能展示速度与位移之间的关系。

matlab 复制代码

figure;
plot(x(:, 1), x(:, 2));
title('正常状态相图');
xlabel('位移 (m)');
ylabel('速度 (m/s)');

轴心轨迹、频谱图、包络谱图、滚道接触力

轴心轨迹绘制需要考虑多自由度模型，频谱图可以通过傅里叶变换得到，包络谱图则用于提取故障特征频率的调制信息，滚道接触力可以通过动力学模型进一步推导计算并绘制。具体代码如下：

matlab 复制代码

% 频谱图
figure;
X = fft(x(:, 1));
f = (0:length(X)-1)*(1/(t(2)-t(1)))/length(X);
plot(f(1:length(X)/2), 2/length(X)*abs(X(1:length(X)/2)));
title('频谱图');
xlabel('频率 (Hz)');
ylabel('幅值');

% 包络谱图
% 先对信号进行希尔伯特变换得到解析信号
analytic_signal = hilbert(x(:, 1));
envelope_signal = abs(analytic_signal);
figure;
E = fft(envelope_signal);
plot(f(1:length(E)/2), 2/length(E)*abs(E(1:length(E)/2)));
title('包络谱图');
xlabel('频率 (Hz)');
ylabel('幅值');

% 轴心轨迹（假设多自由度模型，这里仅示意简单二维情况）
% 假设 x1, x2 分别为两个方向位移
figure;
plot(x1(:, 1), x2(:, 1));
title('轴心轨迹');
xlabel('X方向位移 (m)');
ylabel('Y方向位移 (m)');

% 滚道接触力计算（假设简单模型，这里仅示意）
% 接触力与位移、刚度等相关
contact_force = k * x(:, 1);
figure;
plot(t, contact_force);
title('滚道接触力');
xlabel('时间 (s)');
ylabel('接触力 (N)');

通过这些模拟数据，我们可以进一步开展故障诊断和剩余寿命预测，例如利用机器学习算法对不同故障类型的特征进行学习和分类，或者通过数据驱动的方法预测轴承的剩余寿命。这样，MATLAB 轴承动力学模拟就成为了机械健康管理中的一个强大工具。