一、核心思路(位运算优化法)
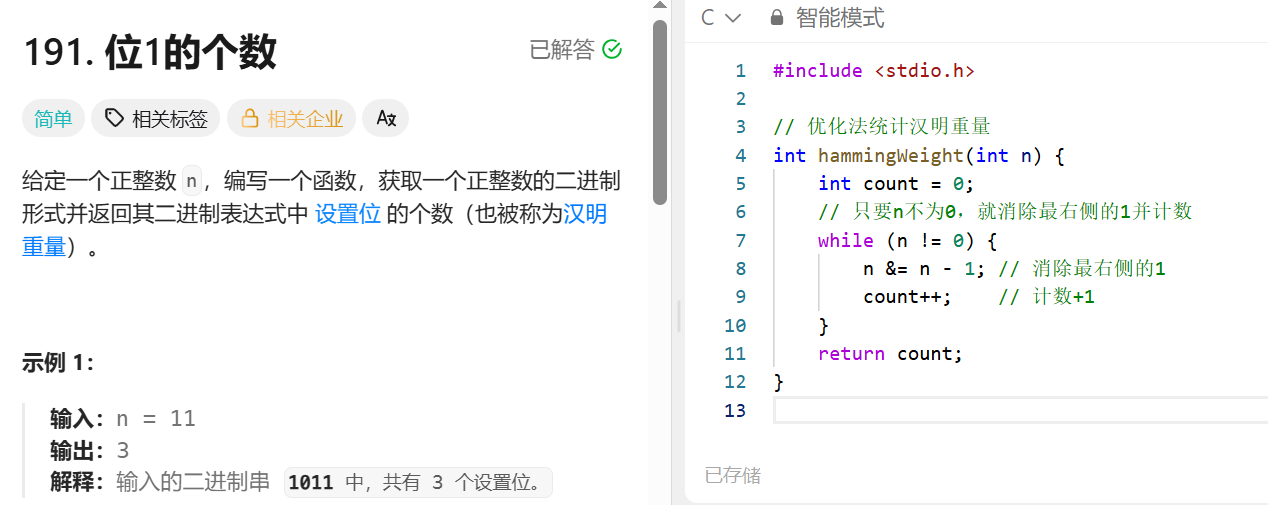
核心是利用位运算特性 n & (n - 1) 消除二进制最右侧的 1,通过统计消除操作的次数,直接得到二进制中设置位(1)的个数。
关键原理推导:
假设 n 的二进制形式为 ...1000(最右侧的 1 后接 k 个 0),则 n - 1 的二进制为 ...0111:
两者做按位与运算 n & (n - 1),结果为 ...0000(最右侧的 1 被消除,右侧的 0 保持不变);
重复该操作,每执行一次就消除一个 1,直到 n 变为 0,操作次数即为 1 的总个数。
示例:n = 11 (1011)
第一次:11 & 10 = 10 (1010) → 消除最右侧 1,计数 = 1;
第二次:10 & 9 = 8 (1000) → 消除第二个 1,计数 = 2;
第三次:8 & 7 = 0 (0000) → 消除第三个 1,计数 = 3;
n=0 结束,最终计数 = 3(与实际 1 的个数一致)。
二、方法优点
- 时间效率极致(理论最优)
循环次数严格等于二进制中 1 的个数,无任何无效循环:
如 n=128 (10000000) 仅需 1 次循环,n=2147483645 (30个1) 仅需 30 次循环;
对比固定遍历 32 位的方法,减少了 "遍历 0 的位" 的无效操作,在 1 的个数较少时(如 n=2、n=4、n=8)效率提升尤为显著。
时间复杂度仍为 O (1)(最多 32 次循环),但实际执行指令数远少于逐位检查法。
- 空间复杂度最优(O (1))
仅使用 1 个计数器变量(count),无需额外开辟数组、字符串等存储结构,也无需循环索引变量(如逐位检查法的i),内存占用达到极致,适合内存受限的嵌入式、单片机等场景。
- 位运算原生高效
n & (n - 1) 是 CPU 原生支持的位运算,执行周期仅 1 个时钟周期,远快于算术运算、数值转换等操作;
无中间转换环节(如转二进制字符串、转数组),避免了转换过程中的性能损耗和边界错误(如字符串补零、数组越界)。
- 代码简洁且逻辑紧凑
无需控制循环次数(无需for循环的 i 从 0 到 31),仅通过while(n != 0)判断终止条件,代码行数更少,逻辑聚焦 "消除 1 并计数" 核心目标,可读性和可维护性高。
- 鲁棒性强,适配题目约束
题目中1 ≤ n ≤ 2³¹ - 1(32 位正整数),无需处理负数符号位,n & (n - 1) 对正整数的处理无任何漏洞;
即使输入为边界值(如2³¹ - 1,二进制全 1),也能通过 31 次循环正确计数,无溢出或逻辑错误。
三、核心优势总结
该方法的核心竞争力在于 "精准定位 1、无无效操作":
从 "遍历所有位" 的通用思路,升级为 "只处理 1 的位" 的精准思路,最大化减少 CPU 执行次数;
以极简的代码、极致的时空效率,成为 32 位正整数汉明重量统计的最优解,尤其适合高性能要求、高频调用的场景(如算法竞赛、底层系统开发)。