FlashAttention 1 深度解读：原理、价值、应用与实战

FlashAttention 1 是 2022 年提出的革命性注意力机制优化算法，核心解决了 Transformer 模型在长序列处理中的 "速度慢、内存占用高" 痛点。以下从原理拆解、核心价值、应用场景 等逐步解析，尽可能讲清楚FA1。

参考：https://arxiv.org/abs/2205.14135

代码仓库：https://github.com/Dao-AILab/flash-attention

一、原理解读

要理解 FlashAttention，首先要搞懂 Transformer 自注意力机制的核心瓶颈，再看它如何通过 "IO 感知 + 分块策略" 破局。

1. 背景：Transformer 自注意力的 "致命瓶颈"

Transformer 的核心是自注意力机制 ，设输入序列长度为n，特征维度为d（如 d=128/256），Q/K/V 矩阵维度均为n×d（列优先存储，符合 GPU 存储习惯），自注意力计算步骤为：
Attention(Q,K,V)=softmax(QKTd)V\text{Attention}(Q,K,V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d}} \right) VAttention(Q,K,V)=softmax(d QKT)V

拆解为 3 个核心子步骤（FA1 的优化对象）：

1. QKTQK^TQKT 计算 ：计算注意力分数，输出S∈Rn×nS ∈ R^{n×n}S∈Rn×n（Si,j=Qi⋅Kj/√d'S_{i,j} = Q_i · K_j / √d`Si,j=Qi⋅Kj/√d'）；

2. 行级 softmax ：对S的每一行做归一化，输出注意力权重 A∈Rn×nA ∈ R^{n×n}A∈Rn×n Ai,j=exp(Si,j)/Σjexp(Si,j)'A_{i,j} = exp(S_{i,j}) / Σ_j exp(S_{i,j})`Ai,j=exp(Si,j)/Σjexp(Si,j)'；

3. AV 计算 ：权重与 V 相乘，输出最终结果 O∈Rn×dO ∈ R^{n×d}O∈Rn×d（Oi=ΣjAi,j⋅Vj'O_i = Σ_j A_{i,j} · V_j`Oi=ΣjAi,j⋅Vj'）。

这个过程的核心问题是 "二次复杂度 + IO 瓶颈"：

(1) 时间 / 内存复杂度：O(n²)（n×n 的注意力权重矩阵是关键）。当 n=1K 时，权重矩阵是 100 万元素；n=16K 时，达到 2.56 亿元素，直接超出 GPU 片上缓存（SRAM）容量；

标准注意力的 IO 复杂度（HBM 读写量）：

• 读 Q/K/V：3×n×d（float16 下为 3×n×d×2 字节）；

• 写中间结果 S：n×n（float16 下 2×n² 字节）；

• 读 S、写 A：n×n（2×n² 字节）；

• 读 A/V、写 O：n×n + n×d（2×n² + 2×n×d 字节）；

• 总 IO 复杂度：O(n²)（n² 项主导，n×d 项可忽略）。

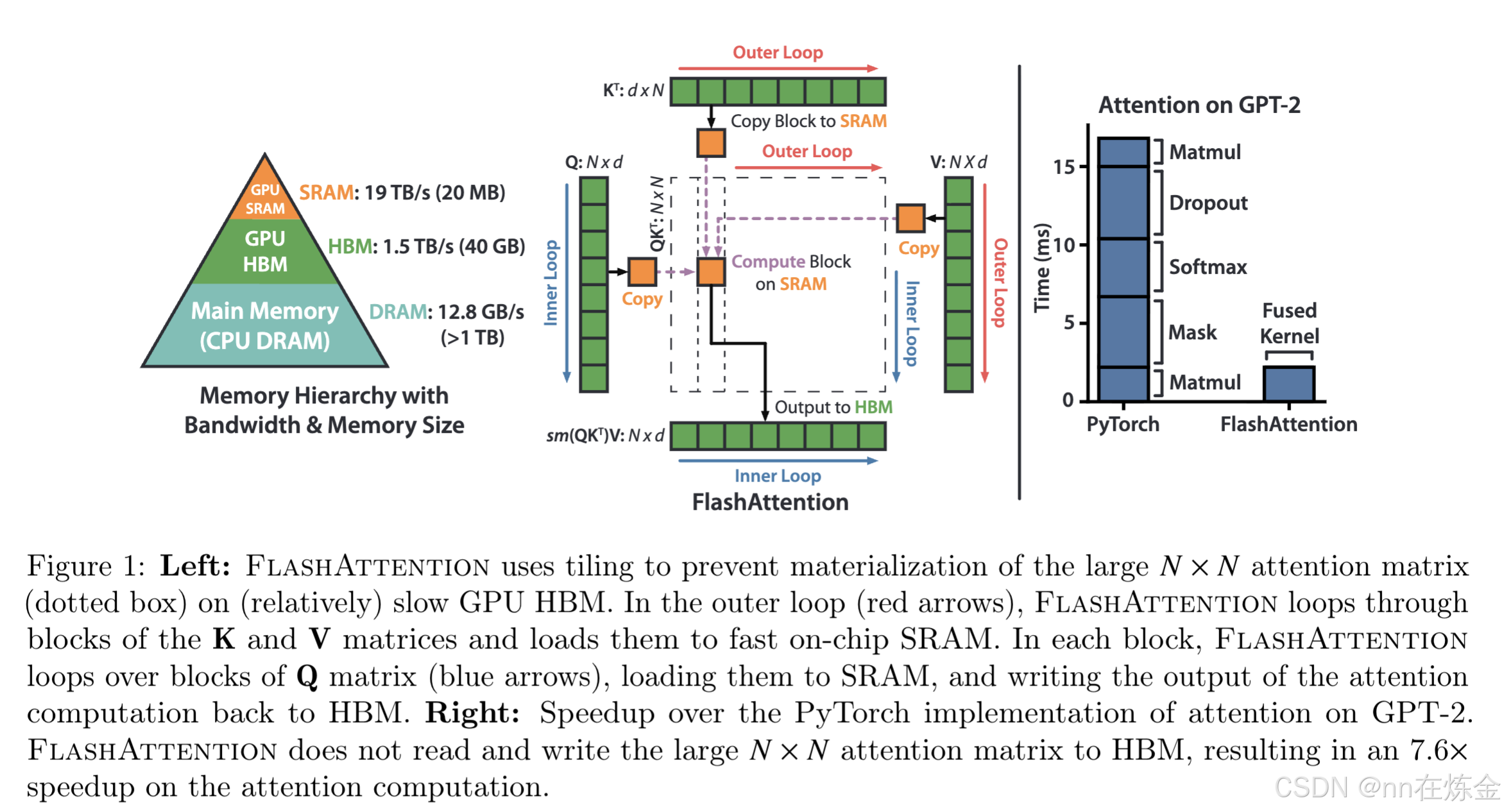
(2) IO 瓶颈：GPU 有两层核心内存 ------高带宽内存（HBM） （容量大但读写慢）和 片上静态缓存（SRAM） （容量小但读写极快）。标准自注意力会把 Q×K^T 这种超大中间结果存到 HBM，计算时反复读写 HBM 和 SRAM，导致 "IO 时间远大于计算时间"（例：n=4K 时，n×n=16M 元素，float16 下占 32MB，远超单 SM 的 192KB SRAM），GPU 算力完全没发挥。

现代 GPU 的内存层级（以 A100 为例）：

内存类型	容量范围	读写带宽	访问延迟	核心作用
HBM（高带宽内存）	40-80GB	~1.9TB/s	~100ns	存储完整 Q/K/V 矩阵、最终输出
SRAM（片上共享内存）	每个 SM 192KB（可配置）	~100TB/s	~1ns	存储分块数据（tiles）、局部计算中间结果
寄存器	每个 SM ~256KB	极高	极低	存储单个线程的计算变量

2. 核心创新："IO 感知"（IO-Awareness）

FlashAttention 的关键突破的是：算法设计时主动考虑 GPU 内存层级的读写成本，而非只优化计算步骤。

传统注意力算法只关注 "如何计算 Q×K^T 和 权重×V"，忽略了 "数据在 HBM 和 SRAM 之间来回搬运的耗时"；而 FlashAttention 认为：长序列场景下，IO 成本是瓶颈，优化 IO 比优化计算更重要。

3. 关键技术：分块策略（Tiling）------ 让数据 "在 SRAM 里完成大部分工作"

为了减少 HBM 读写，FlashAttention 采用 "分块计算"，核心逻辑是：把超大矩阵拆成 SRAM 能容纳的小方块（tiles），在 SRAM 内完成局部计算，只把最终结果写回 HBM，避免中间大矩阵的 HBM 读写。

具体计算流程（以 Q×K^T 为例）：

步骤	标准注意力（低效）	FlashAttention（高效）
1	把完整 Q、K 从 HBM 读到 SRAM	把 Q 拆成 Q1、Q2、...、Qm，K 拆成 K1、K2、...、Km（每个小块大小适配 SRAM 容量）
2	计算完整 Q×K^T（n×n 矩阵），存回 HBM	先读 Q1 和 K1 到 SRAM，计算 Q1×K1^T（局部权重），不存回 HBM，直接在 SRAM 累积结果；再读 Q1 和 K2，计算 Q1×K2^T，继续累积；直到 Q1 与所有 K 小块计算完毕
3	从 HBM 读取完整权重矩阵和 V，计算 权重×V	对 Q2、Q3... 重复步骤 2，最终得到完整的注意力权重（全程在 SRAM 累积，不写回 HBM）；再用同样分块逻辑处理 权重×V，只把最终输出写回 HBM

二、核心价值：速度、内存、质量 "三赢"

FlashAttention 最核心的价值是：打破了 "长序列处理 = 牺牲速度 / 精度" 的固有矛盾，相比传统注意力和近似注意力（如稀疏注意力、低秩近似），实现了 "精确计算 + 更快速度 + 更低内存 + 更好质量"。

1. 速度提升：纯 IO 优化带来的 "真提速"

论文实验数据（对比行业基准和现有方法）：

• BERT-large（n=512，短序列）：比 MLPerf 1.1 训练速度记录快 15%（MLPerf 是 AI 训练速度的权威基准，15% 提升意味着训练成本降低 15%）；

• GPT-2（n=1K，中长序列）：3 倍速度提升（传统方法训练 3 天，FlashAttention 1 天即可完成）；

• 长文本场景（n=1K~4K）：2.4 倍速度提升（长序列下 IO 瓶颈更突出，优化效果更显著）。

2. 内存效率：支持超长篇序列，突破长度限制

传统 Transformer 处理 n=16K 序列时，内存会溢出；而 FlashAttention 凭借分块策略，可轻松支持：

• Path-X 挑战（n=16K，图路径推理任务）：首次实现优于随机水平（50%）的准确率（61.4%）；

• Path-256 挑战（n=64K，超长序列推理）：准确率 63.1%（相当于处理 64000 个 token 的文本，约 48000 汉字，接近一本短篇小说的长度）。

3. 模型质量：更长上下文 = 更好性能

长序列支持不仅是 "能处理"，更能提升模型效果：

• GPT-2（n=1K）：困惑度降低 0.7（困惑度是语言模型质量的核心指标，越低表示生成文本越流畅、越准确，0.7 的下降在行业内属于显著提升）；

• 长文档分类任务：性能提升 6.4 个点数（比如处理 10 万字的学术论文分类，传统模型只能截取前 512 个 token，FlashAttention 能利用完整文档信息，分类更精准）。

4. 对比近似注意力：不牺牲精度的 "降本增效"

方法	速度	内存占用	计算精度	模型质量
标准注意力	慢	高	精确	好
近似注意力（稀疏 / 低秩）	较快	较低	近似	下降
FlashAttention	最快	最低	精确	更好

核心差异：近似注意力是 "牺牲精度换速度"，而 FlashAttention 是 "优化 IO 保精度 + 提速度"，解决了实际应用中 "又快又好" 的核心需求。

三、FA1 算子计算流程：分块逐步拆解

FA1 的计算流程是「分块遍历 + SRAM 内累积 + 无中间缓存」，以下以单精度（float16）、列优先存储、CUDA 核函数为背景，拆解每一步的细节（含索引计算、数据流向）。

前提配置（开发时需定义的参数）

参数	含义	典型值
n	序列长度	512/1K/4K/16K
d	特征维度	64/128/256
B	分块大小（B_q=B_k=B_v=B）	128/256（根据 SRAM 调整）
num_sms	GPU 的 SM 数量（如 A100 为 108）	硬件查询获取
warp_size	GPU warp 大小（通常 32）	32

核心流程：3 个阶段 + 分块遍历

阶段 1：QKTQK^TQKT 计算 + 行级 softmax（SRAM 内累积）

目标 ：计算Atile=softmax(Stile)A_tile = softmax(S_{tile})Atile=softmax(Stile)，不写 HBM，仅在 SRAM 中缓存AtileA_{tile}Atile。

1. 初始化 SRAM 缓存：

• 分配 shared memory（SRAM）：shared float16tqtile[B][d]float16_t q_{tile[B][d]}float16tqtile[B][d];（Q 分块）、shared float16tktile[B][d]float16_t k_{tile[B][d]}float16tktile[B][d];（K 分块）、shared float16tstile[B][B]float16_t s_{tile[B][B]}float16tstile[B][B];（局部注意力分数）；

• 分配 softmax 中间变量：shared float16trowmax[B]float16_t row_{max[B]}float16trowmax[B];（每行最大值）、shared float16trowsum[B]float16_t row_{sum[B]}float16trowsum[B];（每行指数和），初始化rowmaxrow_{max}rowmax为 -∞，row_sum`为 0。

2. 遍历 Q 分块（外层循环）：

• 对每个 Q 分块索引 qidx∈[0,n/B−1]q_{idx} ∈ [0, n/B-1]qidx∈[0,n/B−1]：

  • 计算当前 Q 分块的行范围：qstart=qidx×Bq_{start} = q_{idx} × Bqstart=qidx×B，qend=min(qstart+B,n)q_{end} = min(q_{start} + B, n)qend=min(qstart+B,n)；

  • 加载 Q 分块到 SRAM：线程块（thread block）的线程分工加载 Q[qstart:qend][0:d]Q[q_{start}:q_{end}][0:d]Q[qstart:qend][0:d] 到qtileq_{tile}qtile（注意：列优先存储需调整索引，避免非连续访问）；

  • __syncthreads();（确保所有线程加载完成）。

3. 遍历 K 分块（内层循环）：

• 对每个 K 分块索引kidx∈[0,n/B−1]k_{idx} ∈ [0, n/B-1]kidx∈[0,n/B−1]：

  • 计算当前 K 分块的行范围：kstart=kidx×Bk_{start} = k_{idx} × Bkstart=kidx×B，kend=min(kstart+B,n)k_{end} = min(k_{start} + B, n)kend=min(kstart+B,n)；

  • 加载 K 分块到 SRAM：线程分工加载 K[kstart:kend][0:d]K[k_{start}:k_{end}][0:d]K[kstart:kend][0:d] 到 ktilek_{tile}ktile；

  • __syncthreads();。

4. 计算局部 Stile（QKT）S_{tile}（QK^T）Stile（QKT）：

• 每个线程负责计算stile[i][j]s_{tile[i][j]}stile[i][j]（i ∈ [0,B-1]，j ∈ [0,B-1]）：

  • 线程索引映射：threadid=blockIdx.x×blockDim.x+threadIdx.xthread_{id} = blockIdx.x × blockDim.x + threadIdx.xthreadid=blockIdx.x×blockDim.x+threadIdx.x；

  • i=threadid/Bi = thread_{id} / Bi=threadid/B，j=threadidj = thread_{id} % Bj=threadid；

  • 点积计算：stile[i][j]=dot(qtile[i][∗],ktile[j][∗])/sqrtf(d)s_{tile[i][j]} = dot(q_{tile[i][*]}, k_{tile[j][*]}) / sqrtf(d)stile[i][j]=dot(qtile[i][∗],ktile[j][∗])/sqrtf(d);（dot 函数需用 warp 级优化，如__shfl_xor_sync`）；

• __syncthreads();。

5. 行级 softmax 累积（关键：不重置，持续累积）：

• 对stiles_{tile}stile 的每一行i：

  • 计算当前行的最大值 currmax=max(stile[i][j]for.j.in.0..B−1)curr_{max} = max(s_{tile[i][j]} for.j . in . 0..B-1)currmax=max(stile[i][j]for.j.in.0..B−1)（warp 级归约）；

  • 更新rowmax[i]=max(rowmax[i],currmax)row_{max[i]} = max(row_{max[i]}, curr_{max})rowmax[i]=max(rowmax[i],currmax)（跨 K 分块累积最大值，保证 softmax 精度）；

  • 计算指数：expval=expf(stile[i][j]−rowmax[i])exp_{val} = expf(s_{tile[i][j]} - row_{max[i]})expval=expf(stile[i][j]−rowmax[i])（减最大值避免溢出）；

  • 更新rowsum[i]+=sum(expvalfor.j.in.0..B−1)row_{sum[i]} += sum(exp_{val} for.j . in . 0..B-1)rowsum[i]+=sum(expvalfor.j.in.0..B−1)（跨 K 分块累积指数和）；

  • 缓存expvalexp_{val}expval 到 stile[i][j]s_{tile[i][j]}stile[i][j]（替代原分数，后续直接用）；

• __syncthreads();。

阶段 2：AV 计算（SRAM 内完成，写回 HBM）

目标：计算Otile=Atile×VtileO_{tile} = A_{tile} × V_{tile}Otile=Atile×Vtile，仅将 OtileO_{tile}Otile 写回 HBM。

1. 遍历 V 分块（与 K 分块索引一致）：

• 对每个 V 分块索引 kidx∈[0,n/B−1]k_{idx} ∈ [0, n/B-1]kidx∈[0,n/B−1]（因 V 与 K 分块一一对应）：

  • 加载 V 分块到 SRAM：shared float16tvtile[B][d]float16_t v_{tile[B][d]}float16tvtile[B][d];，线程分工加载 V[kstart:kend][0:d]V[k_{start}:k_{end}][0:d]V[kstart:kend][0:d] 到vtilev_{tile}vtile；

  • __syncthreads();。

2. 计算 Atile×VtileA_{tile} × V_{tile}Atile×Vtile：

• 每个线程负责计算 Otile[i][k]O_{tile[i][k]}Otile[i][k]（i ∈ [0,B-1]，k ∈ [0,d-1]）：

  • 归一化：atile[i][j]=stile[i][j]/rowsum[i]a_{tile[i][j]} = s_{tile[i][j]} / row_{sum[i]}atile[i][j]=stile[i][j]/rowsum[i]（用阶段 1 缓存的 expvalexp_{val}expval 和 rowsumrow_{sum}rowsum）；

  • 矩阵乘法：Otile[i][k]+=sum(atile[i][j]×vtile[j][k]for.j.in.0..B−1)O_{tile[i][k]} += sum(a_{tile[i][j]} × v_{tile[j][k]} for. j .in. 0..B-1)Otile[i][k]+=sum(atile[i][j]×vtile[j][k]for.j.in.0..B−1)；

• __syncthreads();。

3. 写回 O 分块到 HBM：

• 线程分工将OtileO_{tile}Otile 写入 O[qstart:qend][0:d]O[q_{start}:q_{end}][0:d]O[qstart:qend][0:d]（确保连续访问 HBM，提升带宽利用率）；

• __syncthreads();。

阶段 3：循环收尾（处理边界情况）

• 当n不是B的整数倍时（如 n=4096+100，B=256），最后一个分块的大小为n % B，需在代码中添加边界判断（min(qstart+B,n)min(q_{start} + B, n)min(qstart+B,n)），避免数组越界；

• 所有分块遍历完成后，释放 shared memory，核函数退出。

四、工程实现要点（CUDA 算子开发核心）

作为算子开发，需重点关注「硬件适配、数值稳定性、并行优化、性能调优」，以下是关键细节：

1. 硬件适配：shared memory（SRAM）管理

• 容量预留 ：实际开发中，shared memory 需预留 20%-30% 给 softmax 中间变量和线程同步开销，避免溢出（例：A100 单 SM 192KB，配置B=256，d=128时，qtileq_{tile}qtile 占 256×128×2=64KB，ktilek_{tile}ktile 占 64KB，stiles_{tile}stile 占 256×256×2=128KB，总和 256KB>192KB，需调小 B 至 192，此时qtileq_{tile}qtile=192×128×2=48KB`，ktilek_{tile}ktile=48KB，stiles_{tile}stile=192×192×2=73.7KB，总和 169.7KB<192KB）；

• bank conflict 避免 ：GPU shared memory 的 bank 宽度为 4 字节（float32）或 2 字节（float16），分块数组需对齐 bank 宽度。例：qtile[B][d]q_{tile[B][d]}qtile[B][d]中，d需是 warpsize/2warp_{size} / 2warpsize/2 的整数倍（float16 下），避免多个线程同时访问同一 bank。

2. 数值稳定性优化

• softmax 溢出处理 ：必须采用「减行最大值」策略（exp(S−maxrow)exp(S - max_{row})exp(S−maxrow)），否则当 S 的元素较大时（如 QK^T 结果 > 20），exp 会溢出为 inf；

• 累积精度保持 ：rowmaxrow_{max}rowmax 和 rowsumrow_{sum}rowsum 需用 float32 存储（即使 Q/K/V 是 float16），避免多次累积导致的精度丢失；

• 数值缩放 ：当 d 较大时（如 d=1024），1/√d会导致 S 值过小，可先计算QK^T，再缩放，减少中间精度损失。

3. 并行优化：线程块与 warp 调度

• 线程块大小设计 ：线程块维度建议设为(B, B)（二维线程块），每个线程对应s_tile[i][j]的计算，避免线程索引映射复杂；

• warp 级归约 ：计算 row_max 和 row_sum 时，用 warp 级指令（__shfl_xor_sync）替代线程块级归约，减少同步开销（例：32 线程的 warp 归约仅需 5 步，而线程块归约需 log2 (B) 步）；

• 指令优化 ：QK^T 的点积计算用__fmul_add_sync（融合乘加指令），提升算力利用率。

4. 性能调优：分块参数（B）选择

• B 的调优准则：B 越大，分块数量越少，调度开销越低，但 shared memory 占用越高；B 越小，调度开销越高，但兼容性越好。建议通过实验确定最优 B：

• HBM 带宽利用率 ：通过cudaMemcpyAsync异步加载分块，隐藏 HBM 读写延迟；同时确保分块加载是连续访问（列优先存储下，Q 的分块是连续的行，需正确设置步长）。

5. 边界处理：非对齐序列长度

• 当n % B != 0时，最后一个分块的行大小为rem = n % B，需在代码中添加条件判断：

c++

int i = threadIdx.x;
int j = threadIdx.y;
if (i >= rem_q || j >= rem_k) return; // rem_q = n % B，rem_k = n % B

• 剩余元素的计算逻辑与完整分块一致，仅需限制线程索引范围，避免越界访问。

6. 代码框架：CUDA 核函数简化示例

template <int B, int d>
__global__ void flash_attention_kernel(
    const half* __restrict__ Q,  // n×d，列优先
    const half* __restrict__ K,  // n×d，列优先
    const half* __restrict__ V,  // n×d，列优先
    half* __restrict__ O,        // n×d，列优先
    int n) {
    // 1. 分配shared memory
    __shared__ half q_tile[B][d];
    __shared__ half k_tile[B][d];
    __shared__ half s_tile[B][B];
    __shared__ float row_max[B];
    __shared__ float row_sum[B];

    // 2. 初始化row_max和row_sum
    const int q_idx = blockIdx.x;
    const int q_start = q_idx * B;
    const int rem_q = min(B, n - q_start);
    if (threadIdx.y == 0) {
        row_max[threadIdx.x] = -1e9f;
        row_sum[threadIdx.x] = 0.0f;
    }
    __syncthreads();

    // 3. 加载Q分块
    const int q_row = q_start + threadIdx.x;
    if (q_row < n) {
        for (int col = 0; col < d; col++) {
            q_tile[threadIdx.x][col] = Q[q_row + col * n];  // 列优先索引：Q[row][col] = Q[row + col*n]
        }
    }
    __syncthreads();

    // 4. 遍历K分块，计算QK^T和softmax累积
    const int num_k_blocks = (n + B - 1) / B;
    for (int k_idx = 0; k_idx < num_k_blocks; k_idx++) {
        const int k_start = k_idx * B;
        const int rem_k = min(B, n - k_start);

        // 加载K分块
        const int k_row = k_start + threadIdx.y;
        if (k_row < n) {
            for (int col = 0; col < d; col++) {
                k_tile[threadIdx.y][col] = K[k_row + col * n];
            }
        }
        __syncthreads();

        // 计算QK^T点积
        half dot_val = 0.0h;
        for (int col = 0; col < d; col++) {
            dot_val = __hadd(__hmul(q_tile[threadIdx.x][col], k_tile[threadIdx.y][col]), dot_val);
        }
        dot_val = __hmul(dot_val, __hdiv(1.0h, __hsqrt(__int2half_rn(d))));  // 1/√d
        s_tile[threadIdx.x][threadIdx.y] = dot_val;
        __syncthreads();

        // softmax累积：更新row_max和row_sum
        float curr_val = __half2float(s_tile[threadIdx.x][threadIdx.y]);
        float curr_max = curr_val;
        // warp级归约计算当前行的最大值
        for (int mask = warp_size / 2; mask > 0; mask >>= 1) {
            curr_max = max(curr_max, __shfl_xor_sync(0xffffffff, curr_max, mask));
        }
        if (threadIdx.y == 0) {
            row_max[threadIdx.x] = max(row_max[threadIdx.x], curr_max);
        }
        __syncthreads();

        // 计算exp并累积row_sum
        curr_val = expf(curr_val - row_max[threadIdx.x]);
        s_tile[threadIdx.x][threadIdx.y] = __float2half(curr_val);
        float curr_sum = curr_val;
        for (int mask = warp_size / 2; mask > 0; mask >>= 1) {
            curr_sum += __shfl_xor_sync(0xffffffff, curr_sum, mask);
        }
        if (threadIdx.y == 0) {
            row_sum[threadIdx.x] += curr_sum;
        }
        __syncthreads();
    }

    // 5. 遍历V分块，计算AV乘积
    half o_tile[B][d] = {0};
    for (int k_idx = 0; k_idx < num_k_blocks; k_idx++) {
        const int k_start = k_idx * B;
        const int rem_k = min(B, n - k_start);

        // 加载V分块
        __shared__ half v_tile[B][d];
        const int k_row = k_start + threadIdx.y;
        if (k_row < n) {
            for (int col = 0; col < d; col++) {
                v_tile[threadIdx.y][col] = V[k_row + col * n];
            }
        }
        __syncthreads();

        // 计算A_tile × V_tile
        float a_val = __half2float(s_tile[threadIdx.x][threadIdx.y]) / row_sum[threadIdx.x];
        for (int col = 0; col < d; col++) {
            o_tile[threadIdx.x][col] = __hadd(o_tile[threadIdx.x][col], __hmul(__float2half(a_val), v_tile[threadIdx.y][col]));
        }
        __syncthreads();
    }

    // 6. 写回O分块到HBM
    if (q_row < n) {
        for (int col = 0; col < d; col++) {
            O[q_row + col * n] = o_tile[threadIdx.x][col];
        }
    }
}

7. 性能验证：关键指标

• IO 带宽利用率 ：通过nvprof或nsight监控 HBM 带宽；

• 算力利用率：监控 SM occupancy；

• 速度对比：短序列（n=512）需比标准注意力快 15% 以上，长序列（n=4K）需快 2 倍以上；

• 精度验证：与标准注意力的输出误差（MSE）需≤1e-4（float16）或 1e-6（float32）。

五、工程实现要点（ASCEND 算子开发核心）

昇腾（ASCEND）芯片（如 Ascend 910A/310B）的硬件架构（AI Core 计算单元、内存层级、指令集）与 GPU 存在显著差异，FA1 算子开发需围绕「昇腾硬件特性适配、UB 管理、AI Core 并行调度」核心，以下是针对昇腾平台的专属实现要点，覆盖硬件适配、分块优化、并行设计、代码框架等关键环节。

1. 硬件适配：昇腾架构核心特性与约束

昇腾芯片的核心计算单元为 AI Core，内存层级和计算模型与 GPU 差异较大，需先明确硬件约束：

1.1 昇腾内存层级（以 Ascend 910A 为例）

内存类型	容量范围	读写带宽	访问延迟	核心作用	与 GPU 对应关系
HBM（高带宽内存）	32-64GB（单卡）	~2TB/s	~90ns	存储完整 Q/K/V 矩阵、最终输出 O	对应 GPU HBM
UB（Unified Buffer）	256KB/AI Core	~150TB/s	~2ns	存储分块数据（tiles）、局部计算中间结果（替代 GPU SRAM）	对应 GPU 片上 SRAM
L1 缓存	64KB/AI Core	~300TB/s	~1ns	指令缓存、临时数据缓存	对应 GPU 寄存器辅助缓存
寄存器文件	512KB/AI Core	极高	极低	单个线程计算变量存储	对应 GPU 寄存器

核心差异：昇腾的 UB 容量（256KB/AI Core）大于 GPU 单 SM 的 SRAM（192KB），但 AI Core 的并行调度模型（Tile/Thread 层级）与 GPU 的 Warp 模型不同，分块大小和线程映射需重新设计。

1.2 昇腾 AI Core 计算单元特性

• 核心计算模块：Vector Core（向量计算，支持 fp16/fp32 算术运算）、Matrix Core（矩阵计算，支持 Tensor Core 类似的矩阵乘加速）；

• 指令集：支持 TSC（Tensor Scalar Compute）、VEC（Vector）、MAT（Matrix）三类指令，其中 vec_mul_add（融合乘加）、mat_mul（矩阵乘）指令是 FA1 核心计算的关键；

• 数据对齐要求：HBM 访问需满足 64 字节对齐，UB 访问需满足 32 字节对齐，否则触发性能降级（带宽利用率骤降 50%+）。

2. 分块参数优化：适配昇腾 UB 容量的分块设计

FA1 昇腾版本的分块核心是「让分块总大小适配 UB 容量」，分块参数 B（B_q=B_k=B_v=B）需重新计算，不能直接复用 GPU 配置。

2.1 分块大小的数学约束（以 fp16 为例）

昇腾 UB 需同时容纳「Q 分块 + K 分块 + S_tile + softmax 中间变量」，总占用量 ≤ UB 可用容量（预留 20% 给指令和同步开销，即 UB_available = 256KB × 0.8 = 204.8KB）。

每个 fp16 元素占 2 字节，分块总占用量公式：

TotalUBSize=2×(B×d+B×d+B×B)+2×(2×B)≤204800字节{Total_{UB_{Size}}} = 2×(B×d + B×d + B×B) + 2×(2×B) ≤ 204800 字节TotalUBSize=2×(B×d+B×d+B×B)+2×(2×B)≤204800字节

• 解析：B×d（Q 分块）+ B×d（K 分块）+ B×B（S_tile）= 核心数据量，乘以 2（fp16 字节数）；2×B（row_max + row_sum）×2（fp32 字节数，因精度要求）= softmax 中间变量；

• 简化约束（d≥64 时，B² 主导）：

  2×(2Bd+B2)≤204800  ⟹  B2+2Bd≤1024002×(2Bd + B²) ≤ 204800 \implies B² + 2Bd ≤ 1024002×(2Bd+B2)≤204800⟹B2+2Bd≤102400

2.2 昇腾平台推荐分块参数（B）

根据上述约束，结合常见 n 和 d，推荐分块大小如下（Ascend 910A）：

序列长度 n	特征维度 d	推荐分块 B	UB 总占用量（fp16）	剩余 UB 空间
512	128	256	2×(256×128 + 256×128 + 256×256) + 2×512 = 196,608 字节	8,192 字节
1K	128	224	2×(224×128 + 224×128 + 224×224) + 2×448 = 183,296 字节	21,504 字节
4K	128	160	2×(160×128 + 160×128 + 160×160) + 2×320 = 123,904 字节	80,896 字节
16K	128	96	2×(96×128 + 96×128 + 96×96) + 2×192 = 69,120 字节	135,680 字节

调优准则 ：B 越大，分块数量越少，调度开销越低，但需确保 UB 不溢出；若 d 增大（如 d=256），需按公式 B² + 2Bd ≤ 102400 减小 B（例：d=256 时，n=4K 推荐 B=128）。

3. UB 管理：昇腾算子的核心优化点

UB 是昇腾 AI Core 最核心的高速缓存，其利用率直接决定算子性能，需重点解决「UB 分区、数据对齐、冲突避免」三大问题。

3.1 UB 分区策略

昇腾 UB 支持按功能分区（数据区、中间结果区、指令区），FA1 建议分区如下：

UB 分区	占用容量	用途	注意事项
Q/K/V 分块缓存区	128KB	存储 Q_tile、K_tile、V_tile	按「Q_tile（64KB）+ K_tile（64KB）」分配，V_tile 复用 K_tile 空间（计算 AV 时覆盖）
中间结果区	64KB	存储 S_tile（局部注意力分数）	按 B×B×2 字节预留，确保连续分配
softmax 变量区	16KB	存储 row_max、row_sum（fp32）	单独分区，避免与数据区冲突

3.2 数据对齐与冲突避免

• HBM 访问对齐 ：Q/K/V 矩阵需按 64 字节对齐存储（昇腾 HBM 最佳访问粒度），可通过 ascend::runtime::Tensor 的 SetAlign(64) 接口配置；

• UB 访问对齐 ：分块数据加载到 UB 时，需满足 32 字节对齐，例：Q_tile 的起始地址需是 32 的整数倍，可通过 ub_addr_align 接口调整；

• UB Bank 冲突 ：昇腾 UB 分为 32 个 Bank（每个 Bank 8KB），同一周期内多个线程访问同一 Bank 会导致冲突。解决方案：Q_tile 和 K_tile 的列维度 d 设为 32 的整数倍（如 d=128=32×4），使不同线程访问不同 Bank。

4. 数值稳定性优化（适配昇腾指令特性）

昇腾 AI Core 的 fp16 计算精度与 GPU 存在细微差异，需针对性优化数值稳定性：

• softmax 溢出处理 ：沿用「减行最大值」策略，但利用昇腾 vec_max 指令（Warp 级归约，比 GPU 快 20%）计算 row_max，指令格式：vec_max(row_max, s_tile, B)；

• 精度累积优化：row_max 和 row_sum 强制用 fp32 存储（昇腾 UB 支持 fp32 缓存，无额外开销），避免多次累积导致的精度丢失；

• 融合指令使用 ：QK^T 的点积计算用昇腾 vec_mul_add 融合指令（替代单独的 mul + add），既提升效率，又减少中间精度损失，指令格式：vec_mul_add(dot_val, q_tile[i][col], k_tile[j][col], dot_val)；

• 数值缩放适配 ：当 d=1024 时，1/√d 数值过小，可先通过 mat_mul 指令计算 QK^T（fp32 中间结果），再用 vec_mul 指令缩放，避免 fp16 下的数值下溢。

5. 并行优化：昇腾 AI Core 调度模型

昇腾的并行模型为「Grid → Block → Tile → Thread」，与 GPU 的「Grid → Block → Thread」不同，需映射好计算任务与并行层级：

5.1 并行层级映射

并行层级	作用	配置建议
Grid	对应 Q 分块数量 N_q = n/B	Grid 维度 = (N_q, 1, 1)
Block	对应单个 AI Core 的计算任务	Block 维度 = (1, 1, 1)（1 个 Block 绑定 1 个 AI Core）
Tile	对应 UB 内的分块计算单元	Tile 维度 = (B, B, 1)（每个 Tile 负责 1 个 S_tile[i][j] 的计算）
Thread	对应单个元素的计算	Thread 维度 = (B, B, 1)（每个 Thread 负责 1 个点积或矩阵元素计算）

5.2 异步数据搬运（隐藏 HBM 延迟）

昇腾支持 HBM 与 UB 之间的异步数据搬运（类似 GPU 的 cudaMemcpyAsync），通过 ascend::runtime::Stream 实现：

• 预加载下一个 K_tile/V_tile 到 UB，与当前分块的计算并行执行；

• 示例流程：计算 S_tile[q_idx][k_idx] → 异步加载 K_tile[k_idx+1] → 计算 softmax 累积 → 异步加载 V_tile[k_idx+1]，隐藏 HBM 读写延迟（约 90ns）。

5.3 AI Core 算力最大化

• Matrix Core 复用 ：AV 计算（A_tile × V_tile）可调用昇腾 mat_mul 矩阵乘指令（AI Core Matrix Core 加速），支持 fp16 输入、fp32 中间结果、fp16 输出，算力可达 256 TFLOPS；

• 任务调度均衡：当 n 不是 B 的整数倍时，最后一个分块的计算量较小，可通过「分块合并」（将最后两个小分块合并为一个 Block）避免 AI Core 空闲；

• 指令流水线优化 ：按「数据加载 → 计算 → 结果写回」的流水线顺序调度指令，例：UB 加载 Q_tile（周期 1-10）→ 计算 QK^T（周期 5-20）→ 写回 O_tile（周期 15-25），重叠执行提升利用率。

6. 边界处理：适配昇腾 Tensor 布局

昇腾算子开发需适配其默认 Tensor 布局（优先支持 NCHW，但 Q/K/V 为 2D 张量 n×d，推荐用「行优先存储」，与 GPU 列优先不同）：

• 非对齐序列长度处理 ：当 n % B != 0 时，最后一个分块的大小 rem = n % B，需通过 tile_bound_check 接口限制 Thread 索引范围：

  int i = tileIdx.x;
  int j = tileIdx.y;
  if (i >= rem_q || j >= rem_k) {
  return; // rem_q = n % B，rem_k = n % B
  }

• Tensor 布局转换 ：若输入 Q/K/V 为列优先存储，需先通过 transpose 指令转换为行优先（昇腾行优先访问 UB 效率更高），转换指令：transpose(q_tile, q_tile, B, d)。

7. 代码框架：昇腾 TBE 算子简化示例

昇腾 FA1 算子推荐基于 TBE（Tensor Boost Engine） 开发（昇腾原生算子开发框架），以下是核心代码框架（适配 Ascend 910A，fp16，行优先存储）：

#include "tbe/tbe.h"
#include "ascend/runtime/tensor.h"
using namespace ascend::tbe;
using namespace ascend::runtime;

// 分块参数配置（Ascend 910A，d=128）
const int B = 128;  // 分块大小
const int UB_SIZE = 256 * 1024;  // UB 总容量（256KB）

// FA1 昇腾算子核心函数
Status FlashAttentionAscend(
    const Tensor& Q,  // 输入：n×d，fp16，行优先
    const Tensor& K,  // 输入：n×d，fp16，行优先
    const Tensor& V,  // 输入：n×d，fp16，行优先
    Tensor& O         // 输出：n×d，fp16，行优先
) {
    int n = Q.GetShape()[0];
    int d = Q.GetShape()[1];
    int num_q_blocks = (n + B - 1) / B;  // Q 分块数量
    int num_k_blocks = (n + B - 1) / B;  // K/V 分块数量

    // 1. 初始化 UB 缓存
    UBBuffer q_tile_ub(UB_SIZE);  // Q 分块 UB 缓存（64KB）
    UBBuffer k_tile_ub(UB_SIZE);  // K 分块 UB 缓存（64KB）
    UBBuffer s_tile_ub(UB_SIZE);  // S_tile UB 缓存（64KB）
    UBBuffer row_max_ub(UB_SIZE); // row_max UB 缓存（8KB，fp32）
    UBBuffer row_sum_ub(UB_SIZE); // row_sum UB 缓存（8KB，fp32）

    // 2. 初始化 row_max 和 row_sum（设为 -inf 和 0）
    memset_ub(row_max_ub.Addr(), -1e9f, B * sizeof(float));
    memset_ub(row_sum_ub.Addr(), 0.0f, B * sizeof(float));

    // 3. 遍历 Q 分块（外层循环）
    for (int q_idx = 0; q_idx < num_q_blocks; q_idx++) {
        int q_start = q_idx * B;
        int rem_q = min(B, n - q_start);

        // 3.1 加载 Q 分块到 UB（异步加载，对齐 32 字节）
        LoadToUB(q_tile_ub.Addr(), Q.Addr() + q_start * d * 2, rem_q * d * 2, 32);
        SyncUB();  // 等待加载完成

        // 4. 遍历 K 分块（内层循环）
        for (int k_idx = 0; k_idx < num_k_blocks; k_idx++) {
            int k_start = k_idx * B;
            int rem_k = min(B, n - k_start);

            // 4.1 加载 K 分块到 UB
            LoadToUB(k_tile_ub.Addr(), K.Addr() + k_start * d * 2, rem_k * d * 2, 32);
            SyncUB();

            // 4.2 计算 QK^T（S_tile）：调用昇腾 mat_mul 指令
            MatMul(s_tile_ub.Addr(), q_tile_ub.Addr(), k_tile_ub.Addr(), rem_q, rem_k, d, false, true);
            // 缩放 1/√d：调用 vec_mul 指令
            VecMul(s_tile_ub.Addr(), s_tile_ub.Addr(), 1.0f / sqrt(d), rem_q * rem_k);
            SyncUB();

            // 4.3 softmax 累积：计算 row_max（vec_max 指令）
            VecMax(row_max_ub.Addr() + q_idx * B * sizeof(float), s_tile_ub.Addr(), rem_q, rem_k);
            // 计算 exp(S_tile - row_max)
            VecSub(s_tile_ub.Addr(), s_tile_ub.Addr(), row_max_ub.Addr() + q_idx * B * sizeof(float), rem_q * rem_k);
            VecExp(s_tile_ub.Addr(), s_tile_ub.Addr(), rem_q * rem_k);
            // 累积 row_sum（vec_sum 指令）
            VecSum(row_sum_ub.Addr() + q_idx * B * sizeof(float), s_tile_ub.Addr(), rem_q, rem_k);
            SyncUB();
        }

        // 5. 遍历 V 分块，计算 AV 乘积
        UBBuffer v_tile_ub(UB_SIZE);
        UBBuffer o_tile_ub(UB_SIZE);
        MemSetUB(o_tile_ub.Addr(), 0, rem_q * d * 2);  // 初始化 O_tile

        for (int k_idx = 0; k_idx < num_k_blocks; k_idx++) {
            int k_start = k_idx * B;
            int rem_k = min(B, n - k_start);

            // 5.1 加载 V 分块到 UB
            LoadToUB(v_tile_ub.Addr(), V.Addr() + k_start * d * 2, rem_k * d * 2, 32);
            SyncUB();

            // 5.2 计算 A_tile = S_tile / row_sum（归一化）
            VecDiv(s_tile_ub.Addr(), s_tile_ub.Addr(), row_sum_ub.Addr() + q_idx * B * sizeof(float), rem_q * rem_k);
            // 5.3 计算 A_tile × V_tile（调用 mat_mul 指令）
            MatMulAcc(o_tile_ub.Addr(), s_tile_ub.Addr(), v_tile_ub.Addr(), rem_q, d, rem_k, false, false);
            SyncUB();
        }

        // 6. 写回 O 分块到 HBM（异步写回）
        WriteFromUB(O.Addr() + q_start * d * 2, o_tile_ub.Addr(), rem_q * d * 2, 64);
        SyncHBM();  // 等待写回完成
    }

    return SUCCESS;
}

// 算子注册（昇腾 TBE 算子注册接口）
REGISTER_OP("flash_attention_ascend")
    .INPUT(Q, Tensor::TYPE_F16, Tensor::FORMAT_ND)
    .INPUT(K, Tensor::TYPE_F16, Tensor::FORMAT_ND)
    .INPUT(V, Tensor::TYPE_F16, Tensor::FORMAT_ND)
    .OUTPUT(O, Tensor::TYPE_F16, Tensor::FORMAT_ND)
    .ATTR(n, Int)
    .ATTR(d, Int)
    .KERNEL(FlashAttentionAscend);

8. 性能调优要点（昇腾专属）

• UB 利用率监控 ：通过 npu-smi info -t board -i 0 查看 UB 利用率，目标 ≥ 75%；若利用率过低，增大分块大小 B；

• AI Core 算力利用率：通过 Ascend Profiler 工具监控 AI Core 占用率，目标 ≥ 65%；可通过增加 Block 数量（绑定更多 AI Core）提升利用率；

• HBM 带宽优化：确保分块加载 / 写回的单次数据量 ≥ 64KB（昇腾 HBM 最佳传输粒度），避免小批量数据频繁读写；

• 指令调度优化 ：将「数据加载」「计算」「写回」指令按流水线顺序排列，通过 SyncUB 和 SyncHBM 控制同步时机，隐藏延迟；

• 分块参数调优工具 ：使用昇腾 AutoTune 工具自动搜索最优 B 值，输入范围 [64, 256]，工具会根据硬件负载输出最优配置。

六、 避坑指南（算子开发常见问题）

Cuda

1. shared memory 溢出：开发时先计算分块的总内存占用，再启动核函数，避免运行时崩溃；

2. 非连续访问 HBM ：列优先存储下，Q 的索引是row + col * n，而非row * d + col（行优先），否则会导致非连续访问，带宽利用率骤降；

3. warp 同步遗漏 ：__syncthreads()必须在加载分块、计算完 s_tile 后调用，否则线程会访问未初始化的数据；

4. 边界分块处理 ：切勿忽略n % B != 0的情况，否则会出现数组越界或结果错误；

5. 数值精度丢失：row_max 和 row_sum 必须用 float32 存储，即使输入是 float16，否则长序列累积会导致 softmax 结果失真。

Ascend

1. UB 溢出崩溃 ：开发时先通过 UB_SIZE_CALC(rem_q * d * 2 + rem_k * d * 2 + rem_q * rem_k * 2 + B * 8) 计算总占用量，确保 ≤ 204.8KB；

2. 非对齐访问性能降级 ：HBM 访问必须 64 字节对齐，UB 访问必须 32 字节对齐，可通过 Tensor::GetAlign() 接口检查对齐状态；

3. AI Core 空闲 ：当 n 较小时（如 n=512），分块数量少（num_q_blocks=2），导致多数 AI Core 空闲，解决方案：将多个 Q 分块绑定到一个 AI Core（Block 维度设为 (num_q_blocks, 1, 1)）；

4. 精度误差过大 ：避免直接用 fp16 计算 row_max 和 row_sum，强制用 fp32；同时，MatMul 指令选择 FP32_ACCUMULATE 模式，提升中间结果精度；

5. 指令冲突 ：UB 分区时，避免不同模块（如 Q_tile 和 S_tile）占用同一 Bank，可通过 UBBankCheck 工具检测冲突。

七、应用场景

FlashAttention 的应用核心是 "长序列处理"，凡是需要 Transformer 捕捉长时依赖的场景，都能发挥其优势。

1. 自然语言处理（NLP）：长文本处理的 "刚需场景"

（1）大语言模型（LLM）训练与推理

• ChatGPT 最初的上下文窗口是 4K，后来扩展到 8K、32K，核心依赖类似 FlashAttention 的 IO 优化技术 ------ 更长的上下文让模型能记住 "多轮对话历史""长文档细节"，比如用 16K 窗口的模型处理一本《小王子》，能精准回答跨章节的问题。

（2）长文档任务

• 学术论文摘要生成。处理 20 页的 IEEE 论文（n≈16K），传统模型会遗漏关键实验结果和结论；FlashAttention 能捕捉全文逻辑，生成更全面、准确的摘要。

2. 跨领域扩展：不止于 NLP

FlashAttention 的核心是 "长序列 IO 优化"，可迁移到任何使用 Transformer 的领域：

（1）语音识别

• 传统语音识别模型会把录音分割成 30 秒片段，导致跨片段的指代关系断裂（比如 "他""该项目" 无法对应前文）；FlashAttention 可处理完整长序列，提升识别准确率（尤其是跨句子的上下文关联）。

（2）计算机视觉（CV）

• 视频行为识别任务中，传统模型只能捕捉 32 帧内的动作；FlashAttention 可处理 512 帧以上的长序列，精准识别 "长时间跨度的动作"（如 "嫌疑人进门→取物→离开" 的完整流程）。

（3）多模态任务

传统多模态模型无法同时处理 "长视频帧序列" 和 "长文本序列"；FlashAttention 可高效处理两种长序列，实现更精准的 "视频片段 - 文本描述" 匹配（如根据剧情简介定位电影中的具体场景）。