PyTorch自动求导

求导的数学定义

定义

求导是微积分的核心概念，描述函数在某点的瞬时变化率。其数学定义为：若函数y=f(x) 在点x₀的某邻域内有定义，且极限

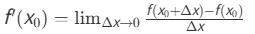
存在，则称f(x) 在x₀处可导，f′(x₀) 为导数。

几何意义

导数的几何意义是曲线在点(x ₀,f(x ₀)) 处切线的斜率。

基本求导公式

常见函数的导数公式包括：

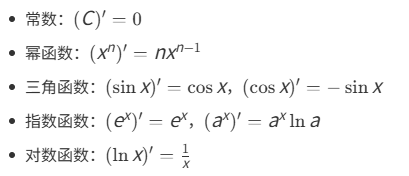
实际应用

导数在物理（如速度、加速度）、经济学（如边际成本）等领域有广泛应用。

PyTorch自动求导

PyTorch的自动求导（Autograd）是其核心功能，能够自动计算张量的梯度，极大简化了神经网络训练中的反向传播过程。

🔧 核心机制

‌动态计算图‌：PyTorch在运行时实时构建计算图，记录所有张量操作历史，支持灵活调试和动态模型结构‌

‌requires_grad属性‌：张量的关键属性，当设置为True时，PyTorch会追踪该张量的所有操作以便后续计算梯度‌。默认情况下为False，即不计算梯度‌。‌梯度计算流程‌：

clike 复制代码

创建可求导张量：x = torch.tensor([1.0], requires_grad=True)‌
执行前向计算操作
调用backward()进行反向传播
梯度自动存储在.grad属性中‌

💡 实际应用示例

clike 复制代码

import torch
# 创建需要计算梯度的张量
x = torch.tensor(3.0, requires_grad=True)
# 前向计算
y = torch.pow(x, 2)  # y = x²
# 反向传播求导
y.backward()
# 查看梯度值
print(x.grad)  # 输出：tensor(6.)

这个例子中，当x=3时，y=x²的导数为2x=6，与计算结果一致‌

🎯 高级功能

梯度控制‌：通过设置requires_grad=False来冻结特定参数，这在多任务学习或迁移学习中非常实用‌。

‌梯度累积与清零‌：多次调用backward()时梯度会累积，需要在参数更新前手动清零：tensor.grad.zero_()^。

✨ 主要优势

代码简化‌：无需手动推导复杂的梯度公式^
‌开发加速‌：减少代码量和潜在错误^
‌灵活性‌：动态图特性适合复杂模型如循环神经网络^

重要函数

PyTorch自动求导主要通过torch.autograd包实现，其中最重要的函数是backward()和grad()。

核心函数简介

backward()函数

标量输出：当输出为单个数值时，直接调用y.backward()即可自动计算梯度
非标量输出：输出为向量或矩阵时，需传入与输出同形的梯度张量，即y.backward(gradient=torch.tensor(...))
梯度累积：默认情况下，多次调用backward()梯度会累加，需要时可用retain_graph=True保留计算图

grad()函数
用于计算指定输出相对于输入的梯度总和，可精确控制梯度计算过程。

关键概念与属性

.requires_grad属性

张量的关键属性，设置为True时PyTorch会追踪所有操作以便后续梯度计算。

梯度控制方法

.detach()：将张量从计算图中分离，不再追踪梯度
torch.no_grad()：上下文管理器，内部所有计算都不需要梯度，常用于模型评估。

计算图机制

PyTorch通过动态构建有向无环图记录所有操作历史，每个张量都有grad_fn属性指向创建它的操作。

使用建议

现在可以尝试创建一个简单的张量，设置requires_grad=True，然后调用backward()函数来实际体验自动求导过程。

grad()函数

函数基本语法

clike 复制代码

torch.autograd.grad(
    outputs,           # 需要求导的函数输出
    inputs,            # 需要计算梯度的输入
    grad_outputs=None, # 各输出的梯度权重
    retain_graph=None, # 是否保留计算图
    create_graph=False, # 是否创建导数计算图
    only_inputs=True,   # 是否只计算指定输入的梯度
    allow_unused=False  # 是否允许输入不参与计算
)

核心参数详解

‌outputs‌：需要求导的张量，可以是标量或向量

‌inputs‌：需要计算梯度的变量列表，函数会计算 outputs 对每个 inputs 中元素的梯度

‌grad_outputs‌：当 outputs 为向量时，需提供与 outputs 同形的张量作为"向量-Jacobian乘积"中的向量相当于链式法则中的外部梯度

‌create_graph‌：设置为 True 时可以计算高阶导数

backward()函数

基本语法

clike 复制代码

tensor.backward(gradient=None, retain_graph=None, create_graph=False)

核心参数详解

‌gradient‌：

当输出为非标量时，需传入与输出同形的张量作为外部梯度

相当于链式法则中的上游梯度
‌retain_graph‌：

默认False，反向传播后释放计算图内存

设为True可保留计算图用于多次反向传播
‌create_graph‌：

默认False，设为True可创建导数计算图，用于高阶导数计算

ps：没学懂，上面都是网上找的东西，留作存档，放在未来在看