VGGT 论文学习

论文链接：https://arxiv.org/abs/2503.11651

代码链接：https://github.com/facebookresearch/vggt

简介

VGGT 是一个强大的、多功能的前馈神经网络模型。它能够从一个、几个甚至上百张同一场景的不同视角图片中，直接推断出该场景的多种关键 3D 属性，包括

相机参数
深度图
点云图
3D 点轨迹（同一个3D点在多张图片中被追踪的轨迹）

VGGT 的主要创新优势在于，

多功能的一体化：这是 VGGT 最大的突破，传统的 3D 视觉模型通常只擅长单一功能（比如只做深度估计，或只做相机定位），而 VGGT 一个模型就能完成多项复杂任务。
简单高效：作为一个前馈神经网络，推理速度非常快，无需复杂的后续优化步骤。它能在一秒内完成场景重建，但效果却比那些需要后续进行"视觉几何优化"的模型更好。
性能卓越：在相机参数估计、多视角深度估计、密集点云重建和 3D 点追踪等多个任务上，都达到了业内顶尖水平。

除了直接进行 3D 重建，研究还表明，将预训练好的 VGGT 模型作为特征提取 backbone（主干网络），可以显著提升其他下游任务的性能，比如：

非刚性点追踪：追踪变形物体（人体、动物）的点。
前馈式新视角合成：快速生成从全新视角看到的场景图像。

VGGT 解决的问题是如何通过一个前馈神经网络，根据一组图像来估计场景的 3D 属性。

传统方法基于几何优化方法，例如 bundle adjustment，该方法是一种迭代优化技术，通过反复微调相机参数和 3D 点位置，使得投影到图像上的误差最小。这个过程虽然精确，但通常计算量大、速度慢。
后来，人们用机器学习（特别是深度学习）来解决一些几何方法难以单独处理的问题，比如特征匹配（在两张图片中找到对应的点）和单目深度预测（从一张图片估计深度）。
当前，机器学习和几何方法结合得越来越紧密。出现了像 VGGSfM 这样的端到端的先进运动恢复结构（SfM）系统。它通过可微分的 bundle adjustment 将神经网络和几何优化模块连接起来，形成一个可以整体训练的网络。

尽管像 VGGSfM 这样方法很先进，但它们仍然依赖视觉几何模块（比如可微分的 bundle adjustment），带来了两个缺点：

增加了系统复杂性，需要设计和集成几何优化模块。
增加了计算成本：迭代优化过程本质还是耗时的。

随着神经网络越来越强大，作者提出一个问题：现在是否终于可以直接用神经网络解决3D任务，而几乎完全避开几何后处理？最近的一些工作如 DUSt3R 和 MASt3R 取得了不错的效果，但这些网络一次只能处理两张图片。当需要重建更多图片时，必须依赖后处理步骤来"融合"多个两两配对的重建结果。这本质上仍然没有摆脱后处理。本文更进一步，无需在后处理步骤中优化 3D 几何。本文通过 Visual Geometry Grounded Transformer，从一个场景的单张或多张图片中实现 3D 重建，一次性预测所有关键的 3D 属性（相机参数、深度图等）。仅需一次前向传播，在数秒内完成重建，而且效果要优于那些需要复杂迭代的传统方法（如 DUSt3R、MASt3R 或 VGGSfM），无需任何后处理。

VGGT 的成功证明，我们无需为 3D 重建任务设计复杂的专用网络。相反，它采用一个相对标准的大型Transformer架构（就像 GPT、CLIP 等模型使用的架构），除了在注意力机制上作了小调整（帧内注意力和全局注意力交替），几乎没有引入任何特定的 3D 结构性偏置。通过在大量3D数据上进行训练，就能成为一个强大的多任务3D基础模型。其关键在于让模型同时学习所有相关的3D属性，这种协同学习反而比单独学习每个任务效果更好，体现了"大模型"思想在3D领域的应用。这标志着3D重建领域开始向自然语言处理（NLP）和2D计算机视觉看齐，采用"预训练大模型"的范式。VGGT的目标是成为一个通用的3D基础模型，就像GPT是文本基础模型一样，可以通过微调来适应各种下游3D任务（如动态点追踪、新视角合成）。

同期，其它的大型 3D 神经网络如 DepthAnything、MoGe 和 LRM 只关注于单目深度估计或新视图合成。然而，VGGT 使用一个共享的主干网络，预测全部的 3D 属性。尽管这些3D属性之间存在信息冗余（例如，有了深度图和相机参数，理论上可以算出点云），但实验证明，让模型同时学习这些相互关联的任务，反而能提高整体精度。任务之间起到了正则化和知识互补的作用。尽管模型被训练为同时输出所有结果，但在实际应用（推理）时，用户可以选择最可靠的输出路径。例如，他们发现用预测出的深度图和相机参数间接计算点云，比直接使用模型输出的点云结果精度更高。这展示了模型在实际部署中的灵活性。

本文主要贡献如下：

提出了大型前馈 Transformer VGGT，给定一个场景的单张或多张图片，仅需几秒即可预测 3D 属性，例如相机内参和外参、点云图、深度图和 3D 点轨迹。
证明 VGGT 的预测结果要优于当前 SOTA 的方法，而这些方法都需要漫长的后处理优化步骤。
同时也证明了，VGGT 搭配 bundle adjustment 后处理，产生的效果甚至优于那些专门解决细分 3D 任务的方法。

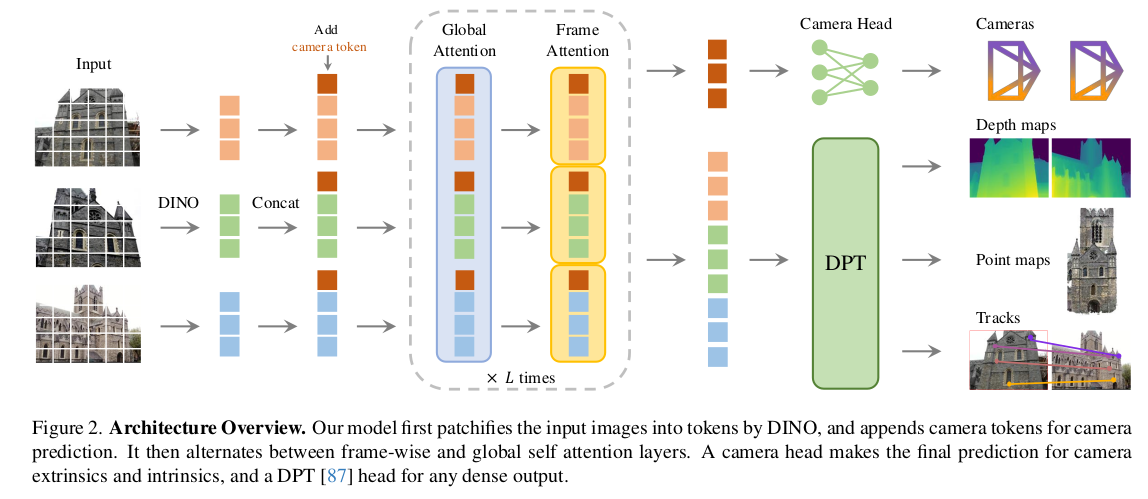
方法

VGGT 是一个大型的 Transformer，输入是一组图像，输出是各种 3D 属性。

问题定义和符号

输入是同一个 3D 场景的一组图像序列 ( I i ) i = 1 N (I_i)_{i=1}^N (Ii)i=1N，包含了 N N N 张 RGB 图像， I i ∈ R 3 × H × W I_i\in \mathbb{R}^{3\times H\times W} Ii∈R3×H×W。VGGT transformer 是一个函数，将这个图像序列映射为对应的 3D 标注，每帧都有对应的一个标注，

f ( ( I i ) i = 1 N ) = ( g i , D i , P i , T i ) i = 1 N f((I_i){i=1}^N) = (g_i, D_i, P_i, T_i){i=1}^N f((Ii)i=1N)=(gi,Di,Pi,Ti)i=1N

Transformer 将每张图片 I i I_i Ii 映射为它的相机参数 g i ∈ R 9 g_i\in\mathbb{R}^9 gi∈R9（内参和外参）、深度图 D i ∈ R H × W D_i\in \mathbb{R}^{H\times W} Di∈RH×W、点云图 P i ∈ R 3 × H × W P_i\in\mathbb{R}^{3\times H\times W} Pi∈R3×H×W，以及一个用于点跟踪的 C 维度的特征图 T i ∈ R C × H × W T_i \in \mathbb{R}^{C\times H\times W} Ti∈RC×H×W。

对于相机参数 g i g_i gi，将旋转四元数 q ∈ R 4 q\in \mathbb{R}^4 q∈R4 和平移向量 t ∈ R 3 t\in\mathbb{R}^3 t∈R3 ，以及 FoV f ∈ R 2 f\in \mathbb{R}^2 f∈R2,拼接到一起得到 g = [ q , t , f ] g=[q,t,f] g=[q,t,f]。在常见的 SfM 框架中，假定相机主点（就是相机光轴（主轴）与图像传感器平面（成像平面）相交的那个点）位于图像的中心。

将图像 I i I_i Ii 的域定义为 I ( I i ) = { 1 , . . . , H } × { 1 , . . . , W } \mathcal{I}(I_i)=\left\{1,...,H\right\}\times \left\{1,...,W\right\} I(Ii)={1,...,H}×{1,...,W}，即像素点位置的集合，它就像一个地址簿。深度图 D i D_i Di关联着每个像素位置 y ∈ I ( I i ) y\in\mathcal{I}(I_i) y∈I(Ii)，它表示了从第 i i i个相机观测，对应的深度值为 D i ( y ) ∈ R + D_i(y)\in\mathbb{R}^+ Di(y)∈R+。点云图 P i P_i Pi 是第 i i i张图像的点云图。对于每个像素位置，点云图 P i P_i Pi 会给出一个三维向量 P i ( y ) ∈ R 3 P_i(y) \in \mathbb{R}^3 Pi(y)∈R3，代表像素所对应的那个点在真实三维空间的位置。最关键的一点是视角不变性，就像DUSt3R论文一样，所有点云图中的 3D 点 P i ( y ) P_i(y) Pi(y) 都被定义在第一个相机 ( g 1 g_1 g1) 的坐标系中。这个坐标系被当作整个场景的世界参考系。如果没有这个统一的坐标系，那么从不同相机视角计算出的3D点会散落在各自相机的局部坐标系中，无法直接拼合成一个完整的3D模型。通过将所有点都转换到第一个相机的坐标系下，它们天生就是对齐的，可以直接用于重建。

最后，对于关键点跟踪 任务，作者遵循了 track-any-point 的方法。你只需要在一张图片 I q I_q Iq上指定一个点 y q y_q yq，VGGT就能自动在所有图片中找到这个点的对应位置，从而形成这个点在所有图片 I i I_i Ii中的运动轨迹 τ ∗ ( y q ) = ( y i ) i = 1 N \tau^\ast (y_q)=(y_i)^N_{i=1} τ∗(yq)=(yi)i=1N。注意，transformer f f f 并不直接输出轨迹，而是特征 T i ∈ R C × H × W T_i \in \mathbb{R}^{C\times H\times W} Ti∈RC×H×W，此特征将用于跟踪。然后，跟踪由一个单独的模块完成，它实现了函数 τ ( ( y j ) j = 1 M , ( T i ) i = 1 N ) = ( ( y ^ j , i ) i = 1 N ) j = 1 M \tau((y_j){j=1}^M, (T_i){i=1}^N)=((\hat{y}{j,i})^{N}{i=1})_{j=1}^M τ((yj)j=1M,(Ti)i=1N)=((y^j,i)i=1N)j=1M， M M M 表示查询点的个数。其输入是查询点 y q y_q yq 和 transformer f f f 预测的密集跟踪特征 T i T_i Ti，然后计算轨迹。网络 f f f 和 τ \tau τ 都是端到端训练的。

预测顺序。输入的图像顺序是任意的，除了将第一张图片作为参考坐标系。网络架构是置换等变的，除了第一帧图像以外，打乱其余输入图像的顺序，不会影响最终的输出结果，只是输出的顺序会跟着输入的顺序发生同样的改变。

过度完备的预测结果 。注意，VGGT 预测的属性不都是独立的。例如在 DUSt3R 中，我们通过解决 PnP 问题，可以从不变的点云图 P P P 推理得到相机的参数 g g g。此外，也可以从点云图和相机参数推理出深度图。在训练时，尽管深度、相机参数和点云图之间存在确定的数学关系（即可相互推导），但强制要求模型同时、明确地预测所有这些东西，能极大地提升模型的整体性能和所学特征的质量。但在模型推理阶段，要得到最准确的3D点云，最可靠的方法是"相信模型预测的深度值和相机参数，然后用几何公式算出3D点"，而不是"直接相信模型为点云任务给出的答案"。

特征主干网络

作者设计了一个简单的架构，不包含复杂的 3D 先验知识，模型能从海量的 3D 标注数据中学习丰富的属性。模型 f f f 是一个大型的 transformer。首先将每张输入图像切分为 K K K 个小块，然后每个小图块经过 DINO 模型，转换为一个 c c c 维的向量，即 t I ∈ R K × C t^I \in \mathbb{R}^{K\times C} tI∈RK×C，称为 token。将所有帧的 tokens 合并为一个大集合 t I = ∪ i = 1 N { t i I } t^I=\cup_{i=1}^N\{t_i^I\} tI=∪i=1N{tiI}，经过网络主体结构。网络主体由多层Transformer块组成，这些块交替使用两种自注意力机制：

帧内自注意力：在这一层，模型只关注同一张图片内部的各个图像块之间的关系。例如，它学习图片中一个桌角和一个桌边之间的相对位置。
全局自注意力：在这一层，模型可以关注所有图片中的所有图像块。例如，它可以将图片1中的一个桌角与图片2、图片3中的同一个桌角进行匹配，从而理解它们是同一个3D点在不同视角下的投影。

通过这种交替，模型既能理解单张图片的内部结构，又能建立不同图片之间的跨视角联系，这正是进行多视图 3D 重建所需的核心能力。

交替注意力。通过引入交替注意力，作者小幅改动了标准的 transformer 设计，让自注意力层在"帧内注意力"和"全局注意力"之间交替进行。这种设计能让模型在一层中专注于理解单张图片的内部结构，在下一层中则专注于建立所有图片之间的对应关系。这种交替循环进行，从而在"单图理解"和"多图关联"之间取得了完美的平衡，并被证明对性能有巨大提升。

帧内自注意力只关注帧内的 tokens t k I t_k^I tkI，它会计算图片内所有 tokens 之间的关系。
全局自注意力则可以看到所有图片的全部 tokens，计算任意两个 tokens 之间的关系，无论它们来自哪张图片，让模型建立跨图片的关联。这是实现多视图3D重建的关键，因为它能让模型发现"图片A中的这个点对应着图片B和图片C中的那个点"。

这样做能在融合帧间信息流和归一化帧内 tokens 的激活值之间取得平衡。如果只用全局注意力，模型可能会过早地陷入混乱，因为它要同时处理所有图片的所有信息，难以先建立对单张图的坚实理解。如果只用帧内注意力，模型则完全无法进行跨视图匹配。交替注意力巧妙地平衡了这一点：先让模型在帧内层深化对单张图的理解，然后在全局层利用这个理解去进行匹配，之后再回到帧内层去 refine，如此反复。模型有多层组成，论文中是 L = 24 L=24 L=24，这些层不是单一的，而是两种注意力模式交替出现，一个简化的顺序可能是：第1层：帧内 -> 第2层：全局 -> 第3层：帧内 -> 第4层：全局 -> ...如此循环。一个重要细节是，VGGT 只使用了自注意力，没有用交叉注意力层。

预测头

这里介绍 f f f 是如何预测相机参数、深度图、点云图和点跟踪的。首先，对于每张输入图像 I i I_i Ii，用特殊的相机 tokens t i g ∈ R 1 × C ′ t_i^g \in \mathbb{R}^{1\times C'} tig∈R1×C′ 和四个 register tokens t i R ∈ R 4 × C ′ t_i^R \in \mathbb{R}^{4\times C'} tiR∈R4×C′ 来增广对应的图像 tokens t i I t_i^I tiI。相机 tokens 代表了图片相机参数的可学习向量，register tokens 可用于存储和传递中间信息，增强模型表达能力。将它们拼接到一起， ( t i I , t i g , t j R ) i = 1 N (t_i^I, t_i^g, t_j^R)_{i=1}^N (tiI,tig,tjR)i=1N 输入进"交替注意力" transformer，输出 tokens ( t ^ i I , t ^ i g , t ^ i R ) i = 1 R (\hat{t}_i^I, \hat{t}_i^g, \hat{t}i^R){i=1}^R (t^iI,t^ig,t^iR)i=1R。第一帧的相机 token 和 register tokens ( t 1 g : = t ˉ g , t 1 R : = t ˉ R ) (t_1^g:=\bar{t}^g, t_1^R := \bar{t}^R) (t1g:=tˉg,t1R:=tˉR) 会被单独初始化为一组特殊的可学习参数，其余帧的相机 token 和 register tokens 共享另一组可学习参数 ( t i g : = t ˉ ˉ g , t i R : = t ˉ ˉ R , i ∈ [ 2 , . . . , N ] ) (t_i^g:=\bar{\bar{t}}^g, t_i^R := \bar{\bar{t}}^R, i\in \left[2,...,N\right]) (tig:=tˉˉg,tiR:=tˉˉR,i∈[2,...,N])。这强制模型将第一帧的相机识别为世界坐标系的原点，所有其他帧的相机参数和 3D 点位置都将相对于这个原点来定义，从而确保了所有预测结果在同一个全局坐标系下对齐（即视角不变）。

注意，除了第一帧的所有帧的相机 tokens 都是相同的可学习参数，模型如何避免混淆，确保第 i i i 帧的相机 tokens 最终学到的是第 i i i 帧的相机参数，而不是其它帧的？这是因为交替注意力 transformer 包含了帧内自注意力层，让 transformer 将相机 tokens 和 register tokens 和图片内对应的 tokens 匹配，tokens 只能与同一帧内的其他 tokens 交互。因此，第 i i i 帧的相机 tokens 只能与第 i i i 帧的图像 tokens 进行信息交换。通过这种层内的反复交互，每个帧的相机 tokens 就会"吸收"专属于自己对应图像内容的几何信息，从而变得帧特定，能够精准地预测出该帧独有的相机参数。Register tokens t ^ i R \hat{t}_i^R t^iR的作用类似于"临时工作区"或"通信中继"，它们在Transformer的注意力过程中帮助传递和整合信息。一旦信息交换完成，它们的任务就结束了。最终的预测任务（相机、深度、点云）由图像 tokens t ^ i I \hat{t}_i^I t^iI和相机 tokens t ^ i g \hat{t}_i^g t^ig 负责。

坐标系 。我们预测相机参数、点云图、深度图都是在第一个相机 g 1 g_1 g1 的坐标系下。所以第一帧相机自身的外参就必须被设定为单位变换。具体来说，就是将其旋转设置为无旋转，即旋转四元数设为 q 1 = [ 0 , 0 , 0 , 1 ] q_1=\left[0,0,0,1\right] q1=[0,0,0,1]。将其平移设置为零平移，即平移向量设为 t 1 = [ 0 , 0 , 0 ] t_1 = \left[0,0,0\right] t1=[0,0,0]。这是通过将第一帧的特殊相机 tokens 初始化为一个独特的可学习向量来实现的， t 1 g : = t ˉ g , t 1 R : = t ˉ R t_1^g := \bar{t}^g, t_1^R := \bar{t}^R t1g:=tˉg,t1R:=tˉR，使得Transformer能够识别出它是第一个相机。

相机预测 。通过四个额外的自注意力层和一个线性层，从输出的相机 tokens ( t ^ i g ) i = 1 N (\hat{t}i^g){i=1}^N (t^ig)i=1N 预测相机参数 ( g ^ i ) i = 1 N (\hat{g}^i)_{i=1}^N (g^i)i=1N。这样就有了预测相机内外参的camera head。

密集预测 。输出图像 tokens t ^ i I \hat{t}i^I t^iI 用于预测密集输出，即深度图 D i D_i Di、点云图 P i P_i Pi 和轨迹特征 T i T_i Ti。首先通过 DPT 层，将 t ^ i I \hat{t}i^I t^iI 转换为密集特征图 F i ∈ R C ′ ′ × H × W F_i \in \mathbb{R}^{C''\times H\times W} Fi∈RC′′×H×W。然后每个 F i F_i Fi 都会通过一个 3 × 3 3\times 3 3×3 卷积层映射为对应的深度图和点云图 D i D_i Di 和 P i P_i Pi。此外，DPT 也输出密集特征 T i ∈ R C × H × W T_i \in \mathbb{R}^{C\times H\times W} Ti∈RC×H×W，作为跟踪头的输入使用。此外，也会预测每个深度图和点云图的不确定图 ∑ i D ∈ R + H × W \sum_i^D \in \mathbb{R}^{H\times W}+ ∑iD∈R+H×W 和 ∑ i P ∈ R + H × W \sum_i^P \in \mathbb{R}^{H\times W}+ ∑iP∈R+H×W。在训练时，在损失函数中使用不确定图；在预测时，它和模型的预测置信度是正比的。

跟踪。为了实现跟踪模块 τ \tau τ，作者使用了 CoTracker2 架构，输入是密集跟踪特征 T i T_i Ti。给定查询图像 I q I_q Iq 中的一个查询点 y j y_j yj（在训练时， q = 1 q=1 q=1，其它图像作为查询图像使用），跟踪头 τ \tau τ 预测所有图像 I i I_i Ii 中的一组 2D 点 τ ( ( y j ) j = 1 M , ( T i ) i = 1 N ) = ( ( y ^ j , i ) i = 1 N ) j = 1 M \tau((y_j){j=1}^M, (T_i){i=1}^N) = ((\hat{y}{j,i}){i=1}^N)_{j=1}^M τ((yj)j=1M,(Ti)i=1N)=((y^j,i)i=1N)j=1M，对应同一个 3D 点 y y y。首先对查询图像的特征图 T q T_q Tq 的查询点 y j y_j yj 做双线性插值，得到它的特征。然后该特征和其它所有的特征图 T i , i ≠ q T_i, i\neq q Ti,i=q 做关联，得到一个关系图集合。这些图会经过自注意力层来预测最终的 2D 点 y ^ i \hat{y}_i y^i，这些点都对应着 y j y_j yj。注意，本跟踪器没有假定任何的输入帧顺序，因此它可以用于任意的输入图像，不只是视频。

训练

损失函数

VGGT 模型 f f f 的训练是端到端的，

L = L c a m e r a + L d e p t h + L p m a p + λ L t r a c k \mathcal{L} = \mathcal{L}{camera} + \mathcal{L}{depth} + \mathcal{L}{pmap} + \lambda \mathcal{L}{track} L=Lcamera+Ldepth+Lpmap+λLtrack

作者发现相机、深度图和点云图有着相同的值域，不需要加权处理。跟踪损失 L t r a c k \mathcal{L}_{track} Ltrack 用系数 λ = 0.05 \lambda=0.05 λ=0.05 做加权。

相机损失 L c a m e r a \mathcal{L}{camera} Lcamera 监督相机参数 g ^ \hat{g} g^的训练： L c a m e r a = ∑ i = 1 N ∥ g ^ i − g i ∥ ϵ \mathcal{L}{camera}=\sum_{i=1}^N \left\| \hat{g}i - g_i \right\|\epsilon Lcamera=∑i=1N∥g^i−gi∥ϵ，使用 Huber 损失来计算预测相机参数 g ^ i \hat{g}_i g^i 和 ground-truth 参数 g i g_i gi 的损失。

带有不确定损失的深度损失 L d e p t h \mathcal{L}_{depth} Ldepth 延续了 DUSt3R，通过预测的不确定性图 ∑ ^ i D \hat{\sum}i^D ∑^iD 来加权预测深度 D ^ i \hat{D}i D^i 和 ground-truth 深度 D i D_i Di 之间的差异。与 DUSt3R 不同，作者也使用了一个基于梯度的项，这广泛用于单目深度估计里面。因此，深度损失定义为： L d e p t h = ∑ i = 1 N ∥ ∑ i D ⊙ ( D ^ i − D i ) ∥ + ∥ ∑ i D ⊙ ( ∇ D ^ i − ∇ D i ) ∥ − α log ⁡ ∑ i D \mathcal{L}{depth}=\sum{i=1}^N \left\| \sum_i^D \odot (\hat{D}i - D_i) \right\| + \left\| \sum_i^D \odot(\nabla \hat{D}i - \nabla D_i) \right\| - \alpha \log{\sum_i^D} Ldepth=∑i=1N ∑iD⊙(D^i−Di) + ∑iD⊙(∇D^i−∇Di) −αlog∑iD，其中 ⊙ \odot ⊙ 是通道逐元素乘积。点云图的损失定义类似，但是包含了点云图的不确定图 ∑ i P \sum_i^P ∑iP： L p m a p = ∑ i = 1 N ∥ ∑ i P ⊙ ( P ^ i − P i ) ∥ + ∥ ∑ i P ⊙ ( ∇ P ^ i − ∇ P i ) ∥ − α log ⁡ ∑ i P \mathcal{L}{pmap} = \sum{i=1}^N \left\| \sum_i^P \odot (\hat{P}_i - P_i) \right\| + \left\| \sum_i^P \odot (\nabla \hat{P}_i - \nabla P_i) \right\| - \alpha \log \sum_i^P Lpmap=∑i=1N ∑iP⊙(P^i−Pi) + ∑iP⊙(∇P^i−∇Pi) −αlog∑iP。

最终，跟踪损失定义为： L t r a c k = ∑ j = 1 M ∑ i = 1 N ∥ y j , i − j y ^ j , i ∥ \mathcal{L}{track}=\sum{j=1}^M \sum_{i=1}^N \left\| y_{j,i}-\hat{jy}{j,i} \right\| Ltrack=∑j=1M∑i=1N yj,i−jy^j,i 。这里，外面的求和是对所有的查询图像 I q I_q Iq 的全部 ground-truth 查询点 y j y_j yj 做的， y j , i y{j,i} yj,i 是 y j y_j yj在图像 I i I_i Ii中的 ground-truth 对应点，而 y ^ j , i \hat{y}{j,i} y^j,i 是跟踪模块中 τ ( ( y j ) j = 1 M , ( T i ) i = 1 N ) \tau((y_j)^{M}{j=1}, (T_i)^N_{i=1}) τ((yj)j=1M,(Ti)i=1N) 预测的对应点。此外，延续了 CoTracker2，使用了一个可见性损失（二元交叉熵损失）来估计一个点是否在给定帧中可见。

Ground Truth Coordinate Normalization

从一个场景的图片中无法确定其绝对大小和全局位置（尺度模糊性），存在无数个等价的正确重建结果。通过数据归一化来消除模糊性，为模型选择一个唯一的、规范的输出格式。在训练时，将所有真值数据统一到第一个相机的坐标系，并根据场景点云的平均尺度进行缩放。与DUSt3R等模型在推理输出后进行归一化不同，VGGT不对网络输出做后处理归一化，而是强制网络在内部学习这种归一化，直接输出符合规范的结果。

3D 重建是从 2D 图像反推 3D 结构。这个过程存在一个七自由度的模糊性（整体平移：3自由度，整体旋转：3自由度，整体尺度：1自由度）。你可以将整个重建场景等比例放大一倍，同时将所有相机远离场景一倍，得到的2D投影图像是完全一样的。因此，有无数个数学上等价的解。为了解决这个问题，必须人为设定一个标准。VGGT采用了和DUSt3R类似的两步标准化法：

设定坐标系，解决平移和旋转模糊性。将所有3D点云和相机的位置，都定义在第一帧相机的坐标系下。这相当于说："我们以第一帧相机的位置为坐标原点 (0,0,0)，以它的朝向为基准方向。" 这解决了全局平移和旋转的模糊性。
设定尺度，解决尺度模糊性。计算 ground truth 点云中所有 3D 点到原点（第一帧相机）的平均欧氏距离，然后用这个距离作为尺子，去归一化相机平移向量 t t t、点云图 P P P 和深度图 D D D。
在 DUSt3R 中，网络 f f f 直接输出一个未经归一化的、尺度任意的 3D 重建结果，然后在推理时需要一个后处理步骤，进行归一化才能得到最终可用的结果。VGGT 在训练阶段，给网络的监督真值已经是归一化后的数据，网络 f f f 训练去直接预测这个归一化后的结果。推理时，网络的前向传播 f ( I ) f(I) f(I) 直接输出的就是归一化后的 3D 重建结果，无需任何后处理。

实现细节

使用了 L = 24 L=24 L=24 层的 Transformer 模型，包含了全局和帧内自注意力机制。模型大约有 12 亿参数。训练时，通过 AdamW 来优化训练损失，整个训练步骤大约有 16 万次迭代。作者使用了余弦退火机制，初始学习率为 0.0002 0.0002 0.0002，在最初的 8000 次迭代中，学习率从 0 0 0 线性增加到峰值 0.0002 0.0002 0.0002。在每个 batch 中，随即从一个场景中选取 2 到 24 帧图像。将图像、深度图和点云图的最大边长缩放为 518 518 518 像素。在 0.33 ∼ 1.0 0.33\sim 1.0 0.33∼1.0 之间随机改变图像的长宽比。随机改变图像的颜色、模糊程度，或转为灰度图。使用了 64 块 A100 显卡训练了 9 天。控制梯度的大小，防止其超过 1.0。使用了 bfloat16 精度和 gradient checkpointing 来确保训练的稳定性、提升 GPU 利用效率。

训练数据

使用了一个大规模、多样的数据集，包括 Co3Dv2、BlendMVS、DL3DV、MegaDepth、Kubric、WildRGB、ScanNet、HyperSim、Mapillary、Habitat、Replica、MVS-Synth、PointOdyssey、Virtual KITTI、Aria Synthetic Environments、Aria Digital Twin 和类似于 Objaverse 的合成数据资产。这些数据集涵盖了多个领域，包括室内、户外场景，有真实场景和合成场景的数据。这些数据集的 3D 标注来源于多个源头，如传感器直接采集的、合成引擎或 SfM 技术。这些数据集在规模性和多样性上可以和 MASt3R 相媲美。

简介

相关工作

SfM

MVS

TAP

方法