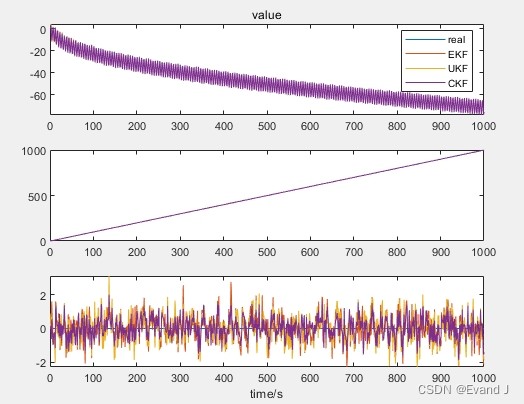
非线性卡尔曼滤波三剑客：EKF、UKF 和 CKF 的 MATLAB 实战对比

【EKF+UKF+CKF对比MATLAB源程序】三种非线性卡尔曼滤波变体：扩展卡尔曼滤波EKF、无迹卡尔曼滤波UKF、容积卡尔曼滤波CKF三种算法的对比。状态更新和观测更新均为非线性的，模拟一定强度的机动性，可用于卡尔曼滤波方法的对比学习，自己修改成运动模型后，可以用于组合导航（GPS+DVL形式）。程序只有一个m文件，我没有把一个文件拆分成多个函数来写，包括各个滤波的自系统都在一个文件里，保证了一个文件运行成功就能得到仿真图像。程序带有中文注释。输出滤波前后的误差图像对比、误差最大值的数值对比。成功，看到就。

在卡尔曼滤波的大家族中，非线性系统的处理一直是个有趣且重要的领域。今天咱们就来深入探讨扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）以及容积卡尔曼滤波（CKF）这三种非线性卡尔曼滤波变体，通过 MATLAB 源程序来看看它们到底有何不同。

背景与应用

这三种滤波算法在很多场景下都大有用武之地。比如在状态更新和观测更新均为非线性的系统里，它们能模拟一定强度的机动性，这对于卡尔曼滤波方法的对比学习来说是绝佳的示例。要是我们进一步修改成运动模型，就像常见的组合导航（GPS + DVL 形式），这些算法能为我们提供准确的状态估计。

MATLAB 源程序剖析

这次的程序简洁明了，就一个 m 文件，所有的滤波自系统都在里面，运行这一个文件就能得到仿真图像，非常方便。

咱们先来看看核心部分，假设状态方程和观测方程如下（这里只是示例方程，实际程序会根据具体场景调整）：

matlab 复制代码

% 状态方程
x = [x(1)+0.1*cos(x(3))*dt;
     x(2)+0.1*sin(x(3))*dt;
     x(3)+x(4)*dt;
     x(4)];
% 观测方程
z = [sqrt(x(1)^2 + x(2)^2); atan2(x(2),x(1))];

在这个状态方程里，位置信息（前两维）会根据角度和速度进行更新，角度和角速度也相应更新。观测方程则是根据位置信息计算距离和方位角。

EKF 实现

matlab 复制代码

% EKF 预测
F = [1 0 0.1*cos(x_hat(3)) 0;
     0 1 0.1*sin(x_hat(3)) 0;
     0 0 1 dt  ;
     0 0 0 1   ];
x_hat = F*x_hat;
P = F*P*F'+Q;

% EKF 更新
H = [x_hat(1)/sqrt(x_hat(1)^2 + x_hat(2)^2) x_hat(2)/sqrt(x_hat(1)^2 + x_hat(2)^2) 0 0;
     -x_hat(2)/(x_hat(1)^2 + x_hat(2)^2) x_hat(1)/(x_hat(1)^2 + x_hat(2)^2) 0 0];
S = H*P*H'+R;
K = P*H'/S;
x_hat = x_hat + K*(z - [sqrt(x_hat(1)^2 + x_hat(2)^2); atan2(x_hat(2),x_hat(1))]);
P = (eye(4)-K*H)*P;

在 EKF 的预测部分，我们先根据状态方程计算状态转移矩阵 F，然后更新状态估计值 x_hat 和协方差 P。在更新部分，计算观测矩阵 H，进而得到卡尔曼增益 K，最后更新状态估计和协方差。

UKF 实现

matlab 复制代码

% UKF 预测
n = size(x_hat,1);
lambda = alpha^2*(n+kappa)-n;
Wm = [lambda/(n+lambda) repmat(1/(2*(n+lambda)),1,2*n)];
Wc = [lambda/(n+lambda)+(1-alpha^2+beta) repmat(1/(2*(n+lambda)),1,2*n)];
sigma_points = [x_hat repmat(x_hat,1,2*n)]+chol((n+lambda)*P)'*[zeros(n,1) eye(n) -eye(n)];
for i = 1:2*n+1
    temp = sigma_points(:,i);
    sigma_points(:,i) = [temp(1)+0.1*cos(temp(3))*dt;
                         temp(2)+0.1*sin(temp(3))*dt;
                         temp(3)+temp(4)*dt;
                         temp(4)];
end
x_hat = sigma_points*Wm';
P = zeros(n);
for i = 1:2*n+1
    P = P+Wc(i)*(sigma_points(:,i)-x_hat)*(sigma_points(:,i)-x_hat)';
end
P = P+Q;

% UKF 更新
sigma_points_z = zeros(2,2*n+1);
for i = 1:2*n+1
    temp = sigma_points(:,i);
    sigma_points_z(:,i) = [sqrt(temp(1)^2 + temp(2)^2); atan2(temp(2),temp(1))];
end
z_hat = sigma_points_z*Wm';
Pzz = zeros(2);
for i = 1:2*n+1
    Pzz = Pzz+Wc(i)*(sigma_points_z(:,i)-z_hat)*(sigma_points_z(:,i)-z_hat)';
end
Pxz = zeros(n,2);
for i = 1:2*n+1
    Pxz = Pxz+Wc(i)*(sigma_points(:,i)-x_hat)*(sigma_points_z(:,i)-z_hat)';
end
S = Pzz+R;
K = Pxz/S;
x_hat = x_hat + K*(z - z_hat);
P = P - K*S*K';

UKF 首先计算 sigma 点，这些点能更好地近似非线性分布。预测阶段，通过 sigma 点更新状态估计和协方差。更新阶段，计算观测相关的 sigma 点，得到预测观测值、观测协方差以及互协方差，从而算出卡尔曼增益并更新状态和协方差。

CKF 实现

matlab 复制代码

% CKF 预测
n = size(x_hat,1);
[Wm,Wc] = cubatureWeights(n);
sigma_points = cubaturePoints(n)*sqrt(n)*chol(P)'+repmat(x_hat,1,2*n);
for i = 1:2*n
    temp = sigma_points(:,i);
    sigma_points(:,i) = [temp(1)+0.1*cos(temp(3))*dt;
                         temp(2)+0.1*sin(temp(3))*dt;
                         temp(3)+temp(4)*dt;
                         temp(4)];
end
x_hat = sigma_points*Wm';
P = zeros(n);
for i = 1:2*n
    P = P+Wc(i)*(sigma_points(:,i)-x_hat)*(sigma_points(:,i)-x_hat)';
end
P = P+Q;

% CKF 更新
sigma_points_z = zeros(2,2*n);
for i = 1:2*n
    temp = sigma_points(:,i);
    sigma_points_z(:,i) = [sqrt(temp(1)^2 + temp(2)^2); atan2(temp(2),temp(1))];
end
z_hat = sigma_points_z*Wm';
Pzz = zeros(2);
for i = 1:2*n
    Pzz = Pzz+Wc(i)*(sigma_points_z(:,i)-z_hat)*(sigma_points_z(:,i)-z_hat)';
end
Pxz = zeros(n,2);
for i = 1:2*n
    Pxz = Pxz+Wc(i)*(sigma_points(:,i)-x_hat)*(sigma_points_z(:,i)-z_hat)';
end
S = Pzz+R;
K = Pxz/S;
x_hat = x_hat + K*(z - z_hat);
P = P - K*S*K';

CKF 同样基于 cubature 点来近似分布。预测和更新步骤与 UKF 类似，只是在点的选取和权重计算上有所不同。

结果展示

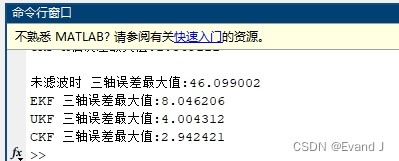
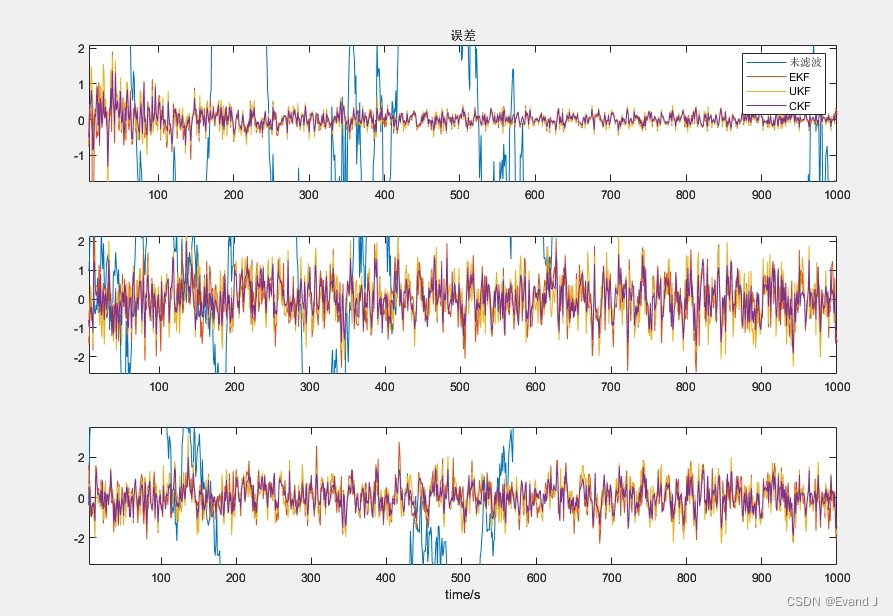
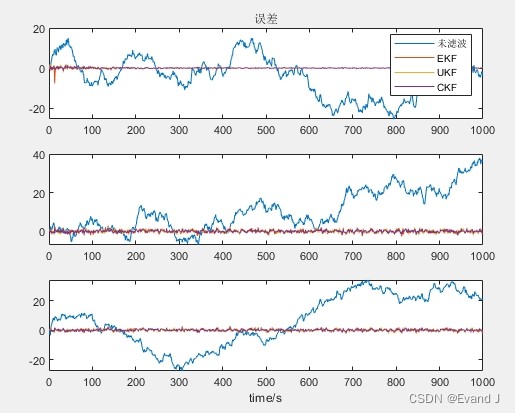
程序运行后，会输出滤波前后的误差图像对比以及误差最大值的数值对比。从误差图像中，我们能直观地看到不同滤波算法在跟踪状态时的表现差异。而误差最大值的数值对比，则为我们提供了更量化的评估指标。

通过这次对 EKF、UKF 和 CKF 的 MATLAB 实现与对比，相信大家对这三种非线性卡尔曼滤波算法有了更深入的理解，在实际应用中就能更得心应手地选择合适的算法啦。