异步电动机变频调速系统设计：仿真技术与文献研究结合，探讨最优调速方案

异步电动机变频调速系统设计全文10653个字。详情请看文章。两个仿真+文章+文献+技术

异步电动机这玩意儿在工业场合真是随处可见，但要让它的转速说变就变可不容易。咱今天不整那些虚头巴脑的理论推导，直接上手拆解变频调速系统的核心设计，顺手用Python和MATLAB给大家整几个活生生的例子。

先说重点，变频调速的关键在于让电压和频率同时变化。这里头最经典的V/F控制法，说人话就是保持电压频率比恒定。咱们用Python模拟个动态调整过程试试：

python 复制代码

import numpy as np

def v_f_control(target_freq, base_voltage=220, base_freq=50):
    ratio = base_voltage / base_freq
    output_voltage = ratio * target_freq
    return min(output_voltage, base_voltage), target_freq

# 测试从10Hz加速到60Hz
for freq in np.linspace(10, 60, 6):
    voltage, _ = v_f_control(freq)
    print(f"频率{freq}Hz时电压:{voltage:.1f}V")

这段代码里藏着两个设计重点：首先是基频以下保持恒转矩的V/F曲线，其次是超过基频后的恒功率区电压限制。跑起来会发现频率超过50Hz后电压不再增加，这时候电机就进入弱磁调速阶段了。

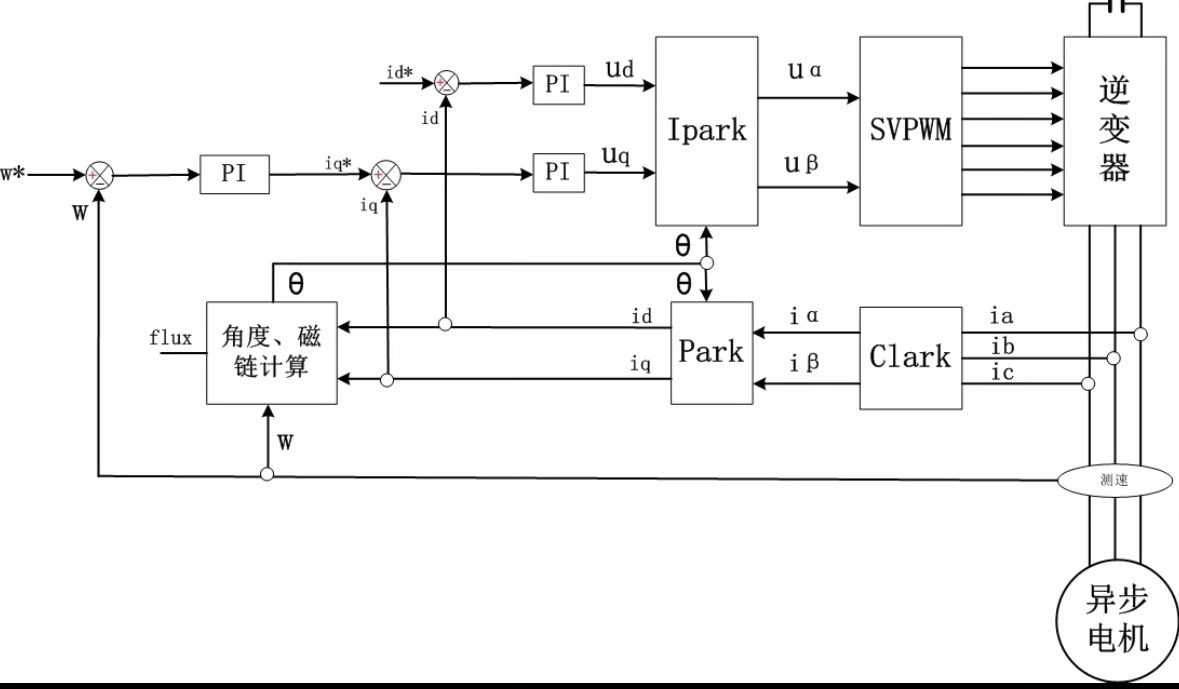
不过V/F控制在动态响应上还是差点意思，这时候就得搬出矢量控制的大招。用MATLAB的Simulink搭建磁场定向控制模型时，关键是要处理好这三个模块：

坐标变换单元（Clarke/Park变换）
电流环PI调节器
SVPWM生成模块

这里有个容易踩坑的地方------转子时间常数的辨识。咱们用遗忘因子递推最小二乘法在线辨识，代码片段长这样：

matlab 复制代码

function [Tr] = identify_tr(u, i, Ts, lambda)
    persistent P theta;
    if isempty(P)
        P = eye(2)*1e3;
        theta = [0;0];
    end
    
    phi = [-i(1) u(1)]';
    K = P*phi / (lambda + phi'*P*phi);
    theta = theta + K*(i(2) - phi'*theta);
    P = (P - K*phi'*P)/lambda;
    
    Tr = theta(2)/theta(1);
end

这个算法的精髓在于用指数加权的方式处理数据，lambda参数控制着新旧数据的权重比例。调试时如果发现辨识结果震荡，八成是lambda取值太大，把0.98调到0.95立马见效。

说到仿真验证，第一个必做的空载启动实验。用PLECS搭建的仿真模型里，注意把PWM载波频率设为3kHz左右，死区时间至少500ns。跑出来的转速波形应该像坐滑梯一样平稳上升，如果出现锯齿状波动，八成是电流环参数没整定好。

第二个关键仿真得做突加负载测试。这里有个骚操作：在电机达到额定转速后，突然给个80%的负载转矩。这时候观察转速跌落如果超过5%，说明速度环的积分时间需要缩短。记得用变步长求解器，把相对误差容限调到1e-5，不然可能漏掉关键动态过程。

文献方面，IEEE Trans on Industrial Electronics那篇《A Comparative Study of Continuous and Discrete Time Observers for Sensorless Induction Motor Drives》必看。作者用龙伯格观测器和滑模观测器做了对比实验，实测发现滑模观测器在低速时的转速估算更稳，不过带来的高频抖动得用二阶滤波器才能压住。

实际调试时，哥总结出三条血泪经验：

死区补偿别迷信公式，拿示波器抓相电压波形最靠谱
过流保护阈值设额定电流的2.5倍，响应时间必须小于10μs
散热片温度超过70℃立即降频运行，IGBT模块比女朋友还娇气

最后给大家看个真实的工程代码片段，这是用STM32F407实现的SVPWM算法核心：

c 复制代码

void SVPWM_Update(float u_alpha, float u_beta) {
    // 扇区判断
    int sector = 0;
    if(u_beta > 0) sector |= 1;
    if((u_alpha*0.8660254f) > (0.5f*u_beta)) sector |= 2;
    if((-u_alpha*0.8660254f) > (0.5f*u_beta)) sector |= 4;
    
    // 作用时间计算
    float t1 = (sqrt3*u_alpha - u_beta) * Ts / Udc;
    float t2 = (2*u_beta) * Ts / Udc;
    // 这里省略了饱和处理代码...
    
    // 写入比较寄存器
    TIM1->CCR1 = (uint32_t)(t1 * PWM_PERIOD);
    TIM1->CCR2 = (uint32_t)(t2 * PWM_PERIOD); 
}

这段嵌入式代码里藏着三个硬件细节：sqrt3用0x6ED9的Q15格式定点数更高效，Ts是PWM周期得和定时器同步，Udc必须实时监测母线电压。要是发现三相电流不对称，先查这个函数里的扇区判断逻辑准不准。