🎈主页传送门:良木生香
🌟志不立，天下无可成之事
目录
本专栏前言：
古人云："欲向锋前陈锦绣，先从纸上灿珠玑"，在进行下一阶段的学习之前，我想先写一段前言。
在之前的学习中，我们将C语言的基本知识进行了系统的学习（但是博客没有进行及时的更新，后面会补上的嘻嘻嘻），那么接下来我们就将会进入到初阶数据结构与算法的学习，在学习数据结构之前，我们要将C语言中的指针（一级指针，二级指针）、函数、结构体，动态内存管理、函数栈帧的创建与销毁先进行系统性的学习之后才能在数据结构中游刃有余，不会显得非常吃力，我也会将这一部分的内容陆续更新到我的博客当中。在数据结构的学习中，我同时也会将数据结构相关的知识点发布到我的博客当中，希望大家一起努力！！！
正文：
一、数据结构与算法的介绍：
在学习数据结构和算法之前，肯定有小伙伴很疑惑，为什么许多书籍会将数据结构与算法这两个东西捆绑在一起呢？那么现在我就来介绍一下这两个东西~~~
(一)数据结构
数据结构,英文名(Data Structure)是计算机存储,组织数据的方式指,指的是相互之间存在一种或者多种特定关系的数据元素的集合.数据的类型繁多,没有一种数据结构能够适用所有的场景,所以我们要学习各种各样的数据结构,像线性表、图、哈希等等
(二)算法
算法(Algiirithm)指的是通过定义良好的计算过程,将一个或者多组的数据输入后,按照相对应的规则输出一个或者多组数据,达到想要的效果
像我们之前写的冒泡排序就是算法的一种,这个算法的作用是将无序的数组排序成有序的数组,当然,不只有冒泡排序这一种算法,还有许许多多的算法能够实现这个功能,但是怎么判断这个算法是否符合我们的要求或者是在某种情况下的效率最高,这就设计到我们这篇文章的重点--复杂度了
(三)学好数据结构与算法的重要性
数据结构与算法,这两个东西在基础的计算机学习中起到了承上启下的作用,承接了C语言,同时开启计算机网路,操作系统等等知识的学习做了铺垫.
在考研中,许多高校的自命题都喜欢考数据结构,408四大课程中数据结构的分数占比最高;在大厂的求职面试中,数据结构与算法的知识也是常考不断,所以学好数据结构与算法是之至关重要的
如何学好数据结构???
1.死磕代码!!!!!两眼一睁就是敲代码,改代码
2.画图画图!!!!遇到不会的,抽象的知识点就要通过画图来解决问题
二、如何衡量一个算法的好坏呢???
这就是这篇文章的重点了,在开始这个知识点的讲解之前,我们先通过一道题目来引入这个话题,题目是:力扣-189:旋转数组
根据题目意思,是想让我们将数组中的元素进行向右旋转,即将前n个元素丢到数组末尾,将剩下的元素进行前移,现在我们的思路是,将数组的元素向后移动N组,每组移动一个元素,图解如下:
下面上代码:
cpp
void rotate(int* nums, int numsSize, int k) {
while(k--){
int temp = nums[numsSize-1];
for(int i=numsSize-1;i>0;i--){
nums[i] = nums[i-1];
}
nums[0] = temp;
}
}在力扣上的运行结果如下:
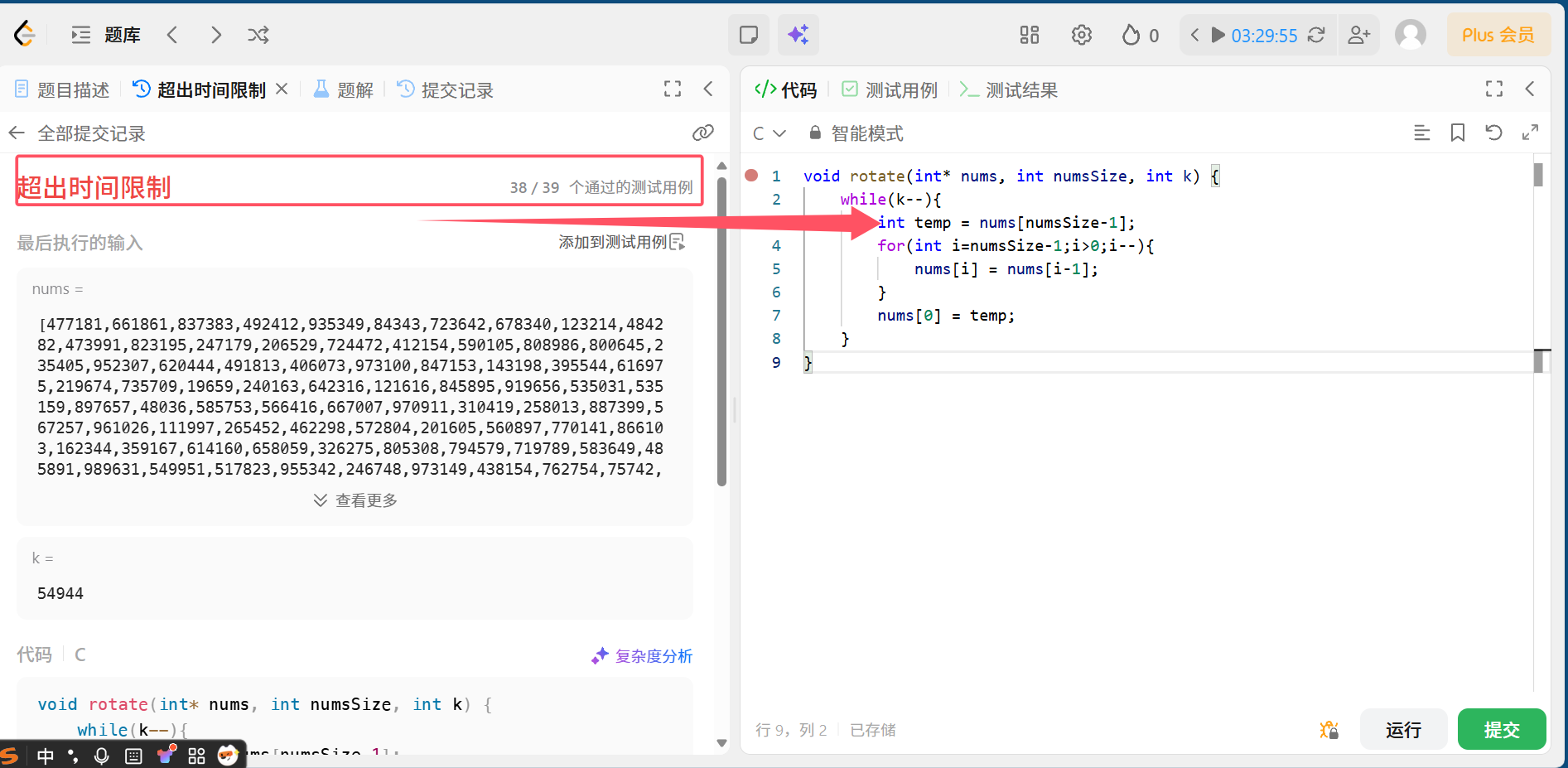
由此可见,我们的思路是对的,但是代码过于暴力了,导致运行时间超出了限制,那对于现在这道题目来说,这个算法就是不好的,那么下面我们就来讲讲判断代码好坏的基本标准~~~
(一)复杂度
我们都知道,计算机在运行程序时,都会消耗时间资源和空间(即内存)资源,因此衡量一个算法的好坏,我们通常从时间与空间两个角度进行衡量,那就是我们平常说的时间复杂度与空间复杂度
时间复杂度考虑的是程序运行的快慢程度,空间复杂度 考虑的则是程序在运行时所占用的内存空间的小,由进过几十年的发展,计算机的内存容量现在已经可以到达了很高的容量,并且成本相对较低,所以现在人们对程序的好坏的评判,都更加在乎时间复杂度,而并没有像以前那样这么的关注空间复杂度,而是更加关注时间复杂度
(二)复杂度的意义
算法复杂度不管在校招面试或者是考研中,都是占比非常大的一部分,同时,是用算法思维（效率、权衡、拆解）指导决策与行动，帮我们在有限资源（时间、精力、金钱）下，平衡 "可行性" 与 "最优性"，避免盲目、浪费与风险，本质是一种 "理性优化的思维方式".所以我们要先将复杂度学好,才能设计高效的代码
三、时间复杂度
定义 ： 在计算机科学中，算法的时间复杂度是⼀个函数式T(N)，它定量描述了该算法的运⾏时间,时间复杂度是衡量程序的时间效率.
那么这时候就有人要问了,为什么我们不直接计算程序运行时间呢???那是因为:
1.程序运行的时间与编译环境和设备配置有关系,比如同一个程序,用一个新的编译器与老的编译器运行,在同样机器上运行的时间是截然不同的
2.同一个算法程序,在不同配置上的机器上运行的时间也是截然不同的
3.除此之外,程序的时间只能在程序运行结束之后计算,不能通过运行之前进行预估
那么算法的时间复杂度是⼀个函数式T(N)到底是什么呢？这个T(N)函数式计算了程序的执⾏次数。
我们通过程序代码或者理论思想计算出程序的执⾏次数的函数式T(N)，假设每句指令执⾏时间基本⼀样(实际中有差别，但是微乎其微)，那么执⾏次数和运⾏时间就是等⽐正相关， 这样也脱离了具体的编译运⾏环境。执⾏次数就可以代表程序时间效率的优劣。⽐如解决⼀个问题的 算法a程序T(N) = N，算法b程序T(N) = N^2，那么算法a的效率⼀定优于算法b,因为算法a的执行次数要少于算法b.下面我们通过一个案例来看看时间复杂度怎么回事:
cpp
//看看这段代码一共执行了多少次???
void Func1(int n) {
int count = 0;
for (int i = 0; i < n; i++) {
for (int i = 0; i < n; i++) {
++count;
}
}
for (int k = 0; k < 2 * n; k++)
{
++count;
}
int M = 10;
while (M--) {
++count;
}
}根据代码,我们可以得到这段代码执行次数的表达式:T(N) = *N^*2 + 2 ∗ N+ 10,我们分别计算一下当N的值为10,100,1000时候的T(N)的值:
当N=10:T(N) = 100+20+10 = 130;
当N=100: T(N) = 10000+200+100 = 10210
当N=1000: T(N) = 1000000+2000+200 = 1002010
由此可见,影响T(N)值的关键是N^2,但是在实际的计算当中,我们真的有必要精确计算出程序执行的次数吗?很显然没有必要,就算精确计算出来了,意义也不大,因为不同的一句代码,编译出来的执行语句是不一样的,**我们计算时间复杂度的本质只是想算法程序的增长量级,**所以我们只需要计算能代表程序增长量级的大概执行次数,复杂度的表示通常用大O渐进表示法.\
(一)、大O渐进表示法
大O符号,是数学中用来表示渐进行为的符号,下面是大O渐进表示法的推导规则:
1.在计算时间复杂度时.只保留最高项,去掉最低项,因为当N不断变大时,低阶项对结果的影响越来越小,当N趋近于无穷大时,低阶项就可以忽略不计了
2.如果高阶项存在并且不是1,那么去除这个项的常数项系数,因为当N不断增大时.这个系数对结果的影响越来越小,就可以忽略不计了
3.T(N)中如果没有N相关的项目,只有常数项,那么就用1来代表所有加法常数
那么通过这个推导规则,就可以计算出Func1的时间复杂度为:O(N^2).
(二)、时间复杂度的计算示例
示例1:
cpp
//计算Func2的时间复杂度
void Func2(int N) {
int count = 0;
for (int i = 0; i < 2*N; i++) { //一共循环2*N次
++count;
}
int M = 0;
while (M--) { //这里一共循环10次
++count;
}
printf("%d\n", count);
}那我们先根据代码先写出T(N)的表达式:T(N) = 2*N+10;那么根据大O渐进表达式得时间复杂单独为:O(N)
示例2:
cpp
void Func(int N, int M) {
int count = 0;
for (int i = 0; i< M; ++i) { //这里一共执行M次
++count;
}
for (int i = 0; i < N; i++) { //这里一共执行N次
++count;
}
printf("%d\n", count);
}由代码得:T(N)=M+N,这时候是两个变量进行相加,我们就要对他们进行比较,当N>M时候,时间复杂度为:O,如果M>N,那么时间复杂度为O(M),如果M==N,那么时间复杂度为:O(N);
示例3:
cpp
//计算Func4的时间复杂度:
void Func4(int N){
int count=0;
for(int i=0;i<100;i++{
++count;
}
printf("%d",count);
}根据这段代码,可以发现,这段代码的执行次数是一个常数100,那么根据大O渐进表示法,这段代码的时间复杂度就应该为:O(1),就是将常数变为100.
示例4:
cpp
//计算Func5的时间复杂度
const char* strchr(const char* str, int character) {
const char* p_begin = str;
while (*p_begin !=character) {
if (*p_begin == '\0') {
return NULL;
}
p_begin++;
}
return p_begin;
}由代码可知,这段代码的功能是在字符串str中查找值为character的元素,既然这是一个查找函数,就分为一下几种情况:1.第一次查找就找到了,也就是这个元素在第一个位置; 2.要查找的元素在最后一个位置,那就要查找n次; 3.要找的元素在字符串的中间,那就要查找n/2次........那么这时候我们要怎么计算时间复杂度呢???这就要注意了,大O渐进法一般关注的是算法的上界,即最坏的情况,那么这段代码的时间复杂度是就是O(N)
示例5:
cpp
//计算Func5的时间复杂度
void Func5(int n) {
int cnt = 1;
while (cnt < n) {
cnt *= 2;
}
}这段代码看起来似乎人畜无害,跟上面的代码都很相似.可能很多人下意识都认这段代码的时间复杂度为O(N),但实际上并不是这样的,要不然也不会成为例子(bushi),这段代码的关键就在于循环体中的语句,每循环一次,cnt都自身乘以2,想要计算执行了多少次,那就等价于,cnt要乘以多少次2才得到n,这就得到了一个数学计算公式: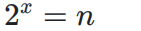
,这既是一个指数运算,可得,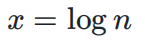
所以这代码的时间复杂度为:O(logn)
示例6:
cpp
//计算Fac的时间复杂度:
long long Fac(size_t n) {
if (n == 0) {
return 1;
}
return Fac(n-1) * n;
}这段代码一眼看到就知道是递归函数,那么我们要怎么计算这种函数呢?很简单,我们就看这函数执行一次的执行次数,在这带代码中,执行一次的执行次数是O(1),我们递归执行n次,那么这段代码的时间复杂度就是O(N)
以上就是我们对于时间复杂度的讲解了,下面我们来看看空间复杂度`~~~~~~
四、空间复杂度
(一)、
空间复杂度也是⼀个数学表达式是对⼀个算法在运⾏过程中因为算法的需要额外临时开辟的空间。 空间复杂度不是程序占⽤了多少bytes的空间，因为常规情况每个对象⼤⼩差异不会很⼤， 所以空间复杂度算的是变量的 个数 。
空间复杂度的计算规则与时间复杂度类似,都是用大O渐进表示法
在这里我们要注意的是,函数运行时所需要的栈空间在编译期间已经是确定好的了,因此空间复杂度主要通过函数在运****行时显式申请的额外空间来确定
(二)、空间复杂度的计算示例
示例1:
cpp
//计算BubbleSort的空间复杂度
void BubbleSort(int* a, int n) {
assert(a);
for (size_t end = n; end > 0; end--) {
int exchange = 0;
for (size_t i = 1; i < end; i++) {
if (a[i - 1] > a[i]) {
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0) {
break;
}
}
}前面我们说过,所有函数所占用的空间在编译的时候都已经确定,现在只用看函数中有哪些白能量是额外申请空间的,我们看到,函数中有exchange等有限个变量重新申请了空间,既然是常数个,那么这段代码的空间复杂度就是O(1).
示例2:
cpp
//计算Fac的空间复杂度:
long long Fac(size_t n) {
if (n == 0) {
return 1;
}
return Fac(n-1) * n;
}根据学习函数栈帧的知识,我们知道,Fac递归了n次,那就是额外开辟了n个函数栈帧,每个栈帧使用了常数个空间,因此这段代码的空间复杂度是O(N).
以上就是我对空间复杂度知识的分享了,希望对大家渔鸥所帮助~~~~~
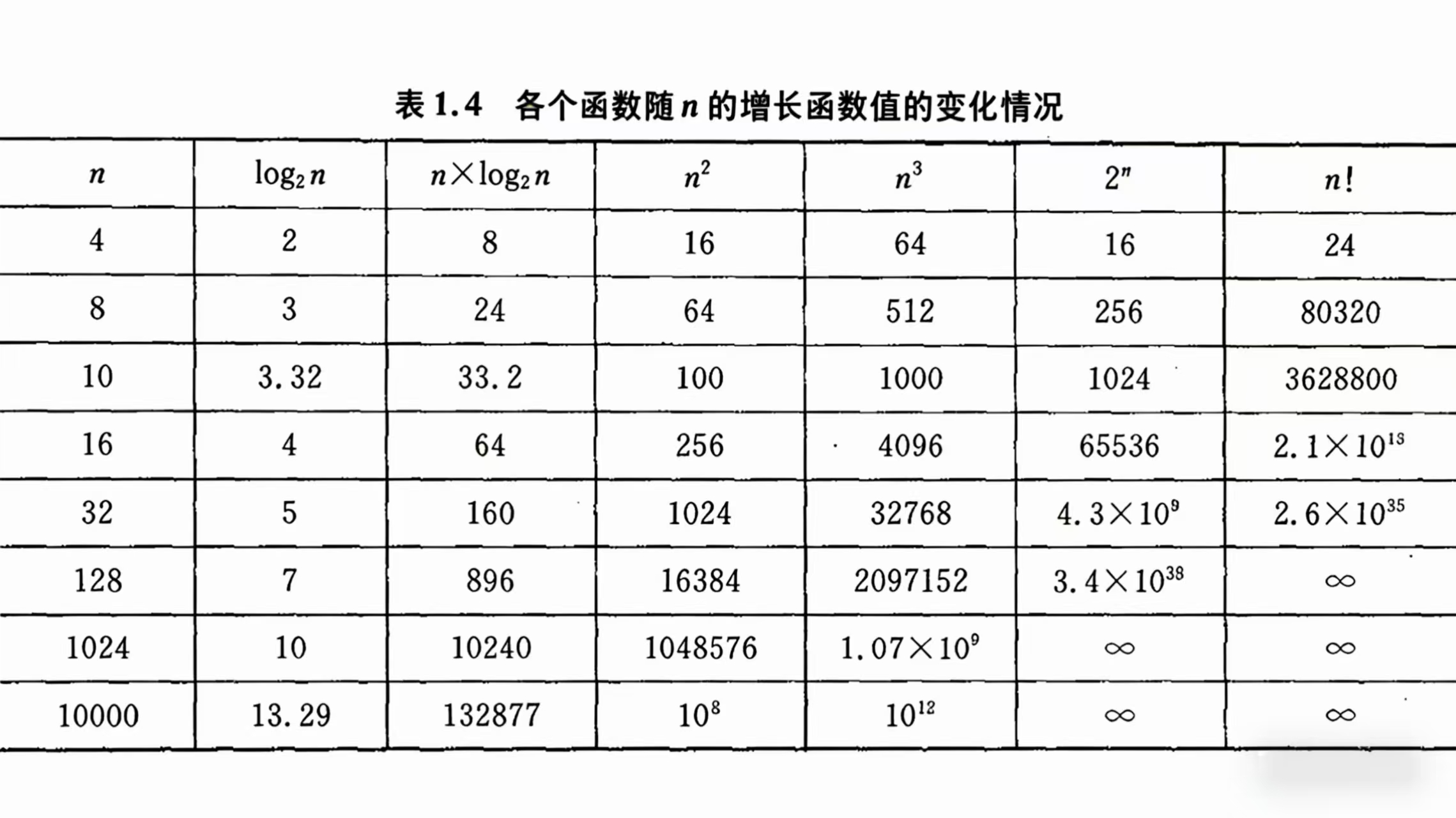
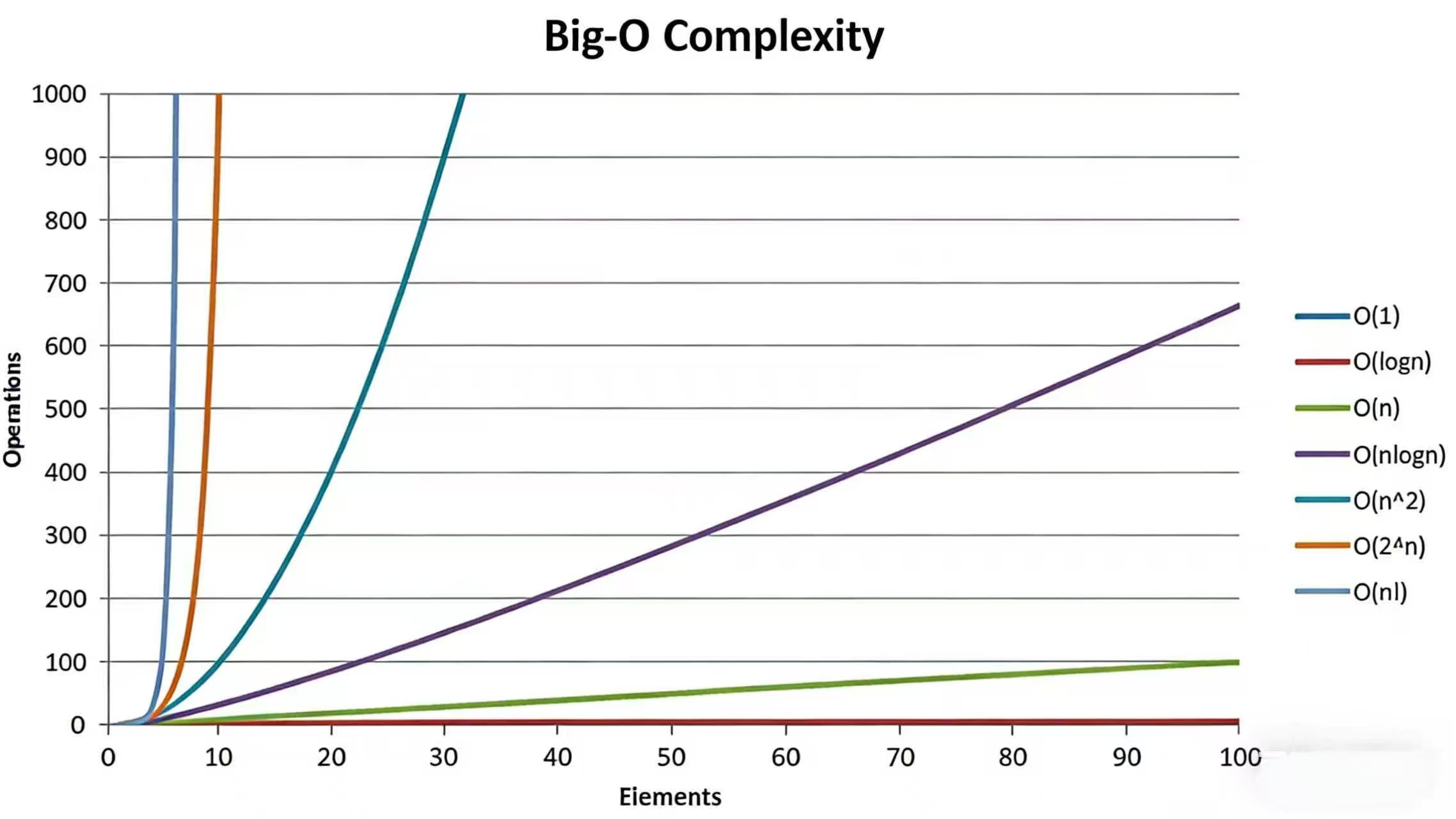
五、常见的复杂度对比
六、回顾例题
在开始讲解复杂度之前,我们引入了一道题目,现在我们已经学会了复杂度的相关知识了,那我们就来分析一下我们写的代码为什么不能被通过以及如何优化代码:
下面是我们之前写的错误代码:
cpp
void rotate(int* nums, int numsSize, int k) {
while(k--){
int temp = nums[numsSize-1];
for(int i=numsSize-1;i>0;i--){
nums[i] = nums[i-1];
}
nums[0] = temp;
}
}现在根据时间复杂度的知识进行计算,得出这段代码的时间复杂度是O(k*n),当k==n的时候,这段代码的时间复杂度就来到了O(n*2),这是非常庞大的数字,这样的代码能通过才怪呢~,那么我们现在就对代码进行整容.
改进代码:
思路一:
新建一个数组,因为是旋转数组,那我们就现将后k个数字先放到新数组中,再将剩下的数字按顺序放到k个数字之后:
思路有了,现在我们将这一部分的代码实现一下:
cpp
void rotate(int* nums, int numsSize, int k)
{
int newarr[numsSize];
//现在将原数组的后k个元素放进新数组的头部
for (int i = 0; i < numsSize; i++) {
newarr[(i + k) % numsSize] = nums[i];
}
//在将新数组拷贝回原数组
for (int i = 0; i < numsSize; i++) {
nums[i] = newarr[i];
}
}这样我们就能计算出,现在的时间复杂度是O(n+n)->O(n),比我们第一次写的好很多了,现在提交看看通过没有: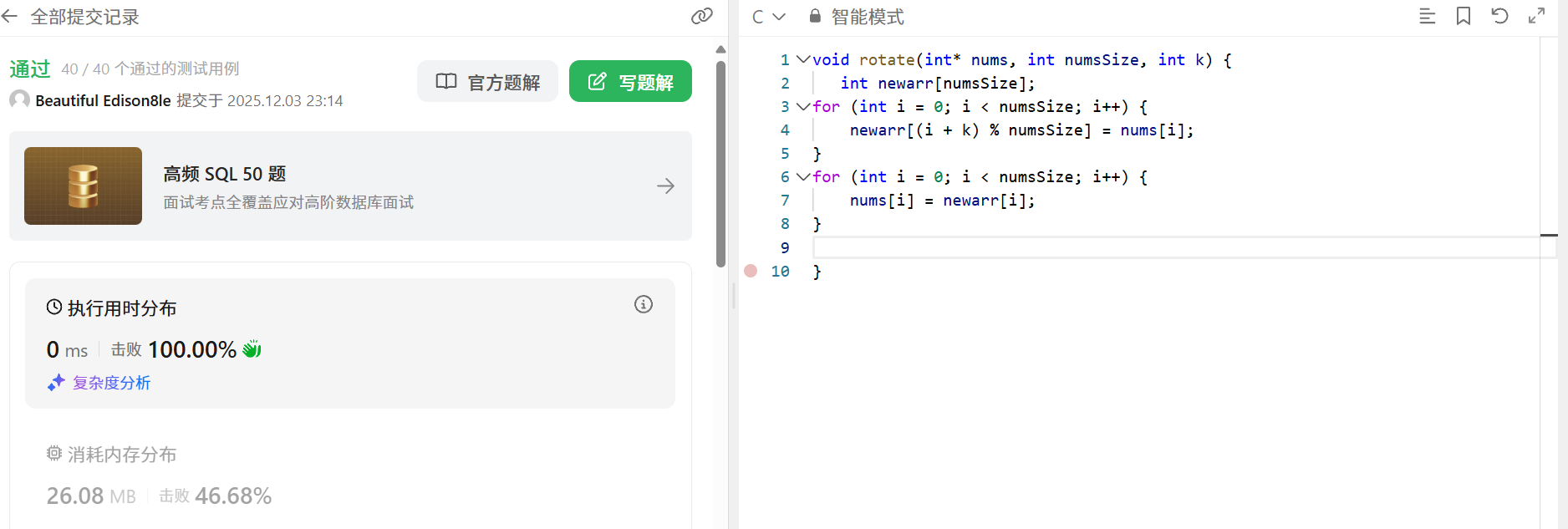
很好,AC了,但是O(n)总觉得还是不够好看,有没有更加好的方法那呢??有的兄弟,有的
思路二:
第三种思路就是,把数组分成两个部分,后k个元素和前n-k个元素,具体的实现看下图:
既然已经有思路了,那我们就继续将代码实现一下:
cpp
//先创建辅助函数--反转数组的函数
void reverse(int* begin, int* end)
{
while (begin < end)
{
//这里使用按位异或的方式将两个数进行交换
/*
*begin = *begin ^ *end;
*end = *begin ^ *end;
*begin = *begin ^ *end;
*/
//也可以使用传统的方法机进行交换：
int temp;
temp = *begin;
*begin = *end;
*end = temp;
begin++;
end--;
}
}
//现在实现旋转函数：
void rotate(int* num, int numSize, int k)
{
int reverse_time = k % numSize;
reverse(num + (numSize - reverse_time), num + (numSize - 1));
reverse(num, num + (numSize - reverse_time - 1));
reverse(num, num + numSize - 1);
}运行结果如下:
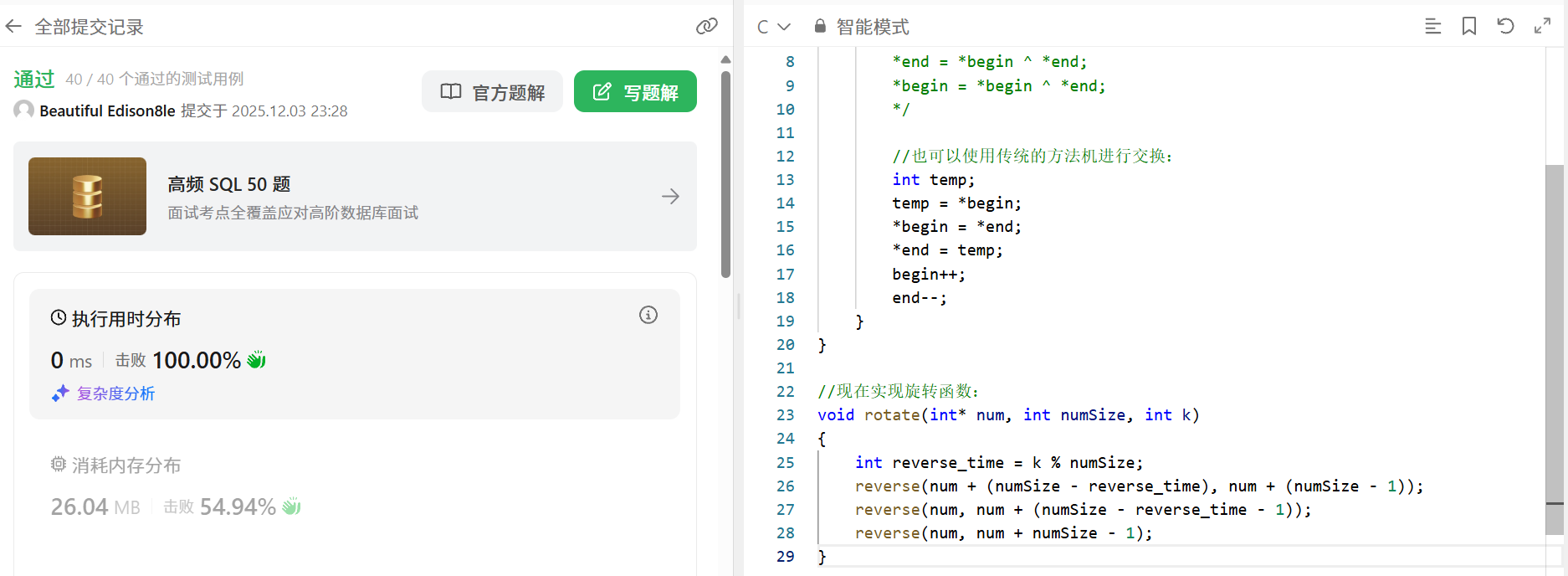
没有悬念的通过了,而且通过计算,这段代码的时间复杂度是O(1),比刚才得代码还要更加高效.
以上就是我对复杂度知识的分享了,有不对地方请大佬们指正~~~~~~
文章是自己写的哈，有啥描述不对的、不恰当的地方，恳请大佬指正，看到后会第一时间修改，感谢您的阅读。