在图像处理与计算机视觉中,轮廓形状的简化与包围区域的计算是常用操作。OpenCV 提供了两个核心函数帮助我们实现这些功能:
- 多边形逼近(Polygon Approximation,
cv2.approxPolyDP) - 凸包(Convex Hull,
cv2.convexHull)
二者点集输入通常来自 cv2.findContours 提取的轮廓,但使用目的和几何意义不同:多边形逼近侧重"简化形状",凸包则是"计算最小凸多边形包围区域"。
多边形逼近(approxPolyDP)
多边形逼近用于在保持轮廓形状基本特征的前提下用更少的顶点表示轮廓 。其核心算法为 Ramer--Douglas--Peucker(RDP)算法,目标是减少不必要的点,从而得到更加紧凑的多边形表示。
RDP 算法核心思想
给定一条由若干离散点组成的折线:
- 连接首尾两点形成一条直线作为基准;
- 找出所有点中 偏离该直线距离最大的点;
- 若最大距离 > 给定阈值 ε(epsilon),则说明折线在该点处发生显著弯曲:
- 将折线分成两段,递归处理;
- 若最大距离 ≤ ε,则说明所有点几乎在同一条直线上,可以直接用首尾点替代中间点。
最终即可得到一个近似该轮廓的较低复杂度折线(多边形)。
ε(epsilon)参数的意义
OpenCV 中的 epsilon 为 逼近精度(容差),常设为周长的某个比例:
python
epsilon = 0.01 * cv2.arcLength(cnt, True)epsilon 越大:
顶点更少,形状更粗略
epsilon 越小:
保留更多细节,顶点更多
多边形逼近的应用场景
- 判断几何形状:三角形、四边形、五边形等;
- 简化物体外轮廓,用于目标识别;
- 动态检测手势(手部轮廓简化);
- 降低计算量(减少点集规模);
- 针对复杂边缘进行平滑处理。
示例
python
import cv2
import numpy as np
img = cv2.imread("shape.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
for cnt in contours:
epsilon = 0.02 * cv2.arcLength(cnt, True)
approx = cv2.approxPolyDP(cnt, epsilon, True)
# 绘制逼近多边形
cv2.drawContours(img, [approx], -1, (0, 0, 255), 2)
cv2.imshow("Polygon Approx", img)
cv2.waitKey(0)执行效果:

凸包(Convex Hull)
凸包(Convex Hull)是指 用最少的点构成一个凸多边形,使所有点都在该多边形内或边界上。
常见比喻:
把钉子钉在木板上,然后用橡皮筋套住所有钉子,最终橡皮筋形成的轮廓就是凸包。
凸包的数学定义
给定一个点集 P,凸包 H§ 是一个满足:
- H§ 是凸集;
- P ⊆ H§;
- H§ 是包含 P 的所有凸集中的最小一个。
OpenCV 默认使用 Graham Scan 或 Andrew's Monotone Chain 算法
凸包算法一般复杂度 O(n log n),核心思想:
- 按 x 坐标(次按 y 坐标)排序;
- 构建上包络(upper hull)和下包络(lower hull);
- 使用几何叉积判断"左转/右转"决定保留或舍弃某些点;
- 合并上下包络形成最终凸包。
凸包的常用用途
- 检测物体的外接凸边界;
- 手势识别(检测手指数量、指尖位置);
- 作为形状特征,计算形状紧致度/凸度;
- 碰撞检测、物理模拟中的包围体。
示例
python
import cv2
import numpy as np
img = cv2.imread("shape.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
for cnt in contours:
hull = cv2.convexHull(cnt)
# 绘制凸包
cv2.drawContours(img, [hull], -1, (255, 0, 0), 2)
cv2.imshow("Convex Hull", img)
cv2.waitKey(0)执行效果:
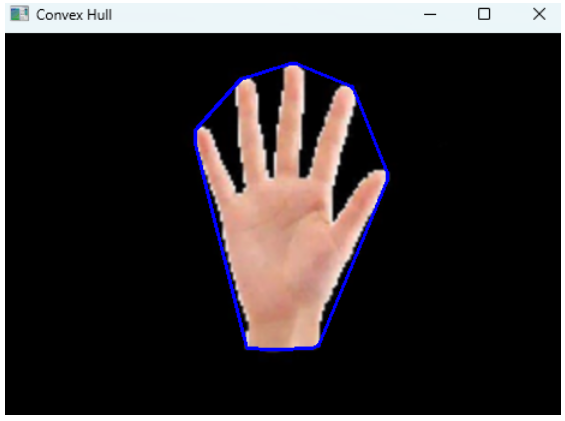
综合示例
python
import cv2
import numpy as np
# -------------------------
# Step 1: 图像读取与预处理
# -------------------------
img = cv2.imread("hand.png") # 输入图像
orig = img.copy()
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
blur = cv2.GaussianBlur(gray, (7, 7), 0)
_, thresh = cv2.threshold(blur, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
# 查找轮廓
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnt = max(contours, key=cv2.contourArea) # 取最大轮廓(手势或主要目标)
# -------------------------
# Step 2: 多边形逼近 approxPolyDP
# -------------------------
epsilon = 0.01 * cv2.arcLength(cnt, True)
approx = cv2.approxPolyDP(cnt, epsilon, True)
# -------------------------
# Step 3: 凸包 convexHull
# -------------------------
# returnPoints=True 返回点坐标(用于绘图)
hull_pts = cv2.convexHull(cnt)
# returnPoints=False 返回索引(用于凸缺陷)
hull_idx = cv2.convexHull(cnt, returnPoints=False)
# -------------------------
# Step 4: 凸缺陷 convexityDefects
# -------------------------
defects = cv2.convexityDefects(cnt, hull_idx)
# -------------------------
# Step 5: 绘制结果
# -------------------------
# ① 绘制原轮廓
cv2.drawContours(orig, [cnt], -1, (0, 255, 0), 2)
# ② 绘制多边形逼近(红色)
cv2.drawContours(orig, [approx], -1, (0, 0, 255), 2)
# ③ 绘制凸包(蓝色)
cv2.drawContours(orig, [hull_pts], -1, (255, 0, 0), 2)
# ④ 绘制凸缺陷点(绿色)
if defects is not None:
for i in range(defects.shape[0]):
s, e, f, depth = defects[i, 0]
start = tuple(cnt[s][0])
end = tuple(cnt[e][0])
far = tuple(cnt[f][0]) # 凸缺陷最深点(凹陷点)
cv2.circle(orig, start, 6, (0, 255, 255), -1) # 起点(指节)
cv2.circle(orig, end, 6, (0, 255, 255), -1) # 终点
cv2.circle(orig, far, 6, (0, 255, 0), -1) # 凹陷处(指缝)
# -------------------------
# Step 6: 显示结果
# -------------------------
cv2.imshow("Threshold", thresh)
cv2.imshow("Contour Analysis", orig)
cv2.waitKey(0)
cv2.destroyAllWindows()执行效果:
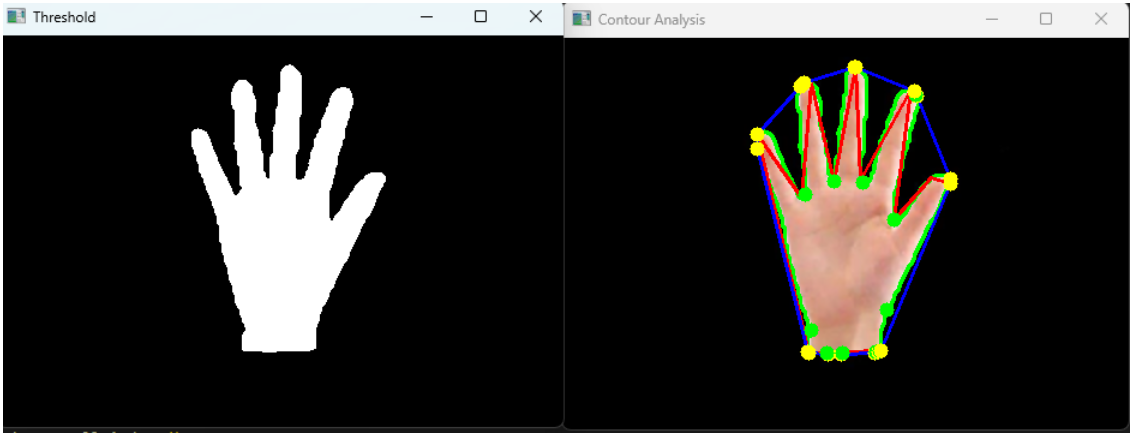
总结
| 对比项 | 多边形逼近(approxPolyDP) | 凸包(convexHull) |
|---|---|---|
| 核心功能 | 轮廓简化 | 计算最小凸包围区域 |
| 输出 | 近似原轮廓的多边形 | 覆盖所有点的最小凸多边形 |
| 是否保持原形状凹陷 | 是 | 否(会"撑平"所有凹陷) |
| 是否保持点顺序 | 是 | 是(可返回索引) |
| 顶点数量 | 取决于 epsilon | 通常较少 |
| 常用场景 | 边缘简化、检测三角/矩形等形状 | 手势分析、碰撞检测、几何包围 |