贝叶斯错误率：机器学习性能的理论极限

本文由「大千AI助手」原创发布，专注用真话讲AI，回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我，一起撕掉过度包装，学习真实的AI技术！
当你训练的图像分类模型准确率高达95%时，一个令人清醒的问题随之而来：剩下的5%错误是模型能力不足，还是问题本身固有的不可逾越的鸿沟？🤔

贝叶斯错误率（Bayes Error Rate， BER）是指在给定特征信息下，任何基于这些特征的分类器所能达到的最低可能错误率，它源于数据分布本身的重叠和噪声，代表了分类问题的固有难度。这个概念是评估机器学习模型性能的黄金标准，能够清晰地区分模型缺陷（可优化部分）与问题本身的固有难度（不可优化部分）。

🔍 贝叶斯错误率是什么？

想象一下你要区分沙滩上的鹅卵石和贝壳：即使视力完美，有些被严重磨损的贝壳看起来也极像鹅卵石，这种固有的混淆就导致了必然的判断错误。在机器学习中，贝叶斯错误率正是这种"必然错误"的理论下限。

从数学上看，对于二分类问题，贝叶斯错误率可表达为：

其中 是在给定特征 时，类别 的真实后验概率。直观地说，对于每个输入 ，最优分类器会选择后验概率最大的类别，而错误率则是"未能选择最大后验概率类别"的概率期望。

📚 理论基础：源于贝叶斯决策理论

贝叶斯错误率深深植根于贝叶斯决策理论（Bayesian Decision Theory）。该理论的核心是在不完全信息下，利用贝叶斯公式将先验知识与观测数据结合，计算出后验概率，并依此做出风险最小的决策。

• • 核心流程：基于已知的类条件概率密度和先验概率 → 利用贝叶斯公式转换为后验概率 → 根据后验概率大小进行决策分类。

• • 最优决策准则：即"最大后验概率准则"，它为每个样本选择具有最高后验概率的类别。

• • 理论结论 ：遵循此准则得到的分类器，其错误率就是所有可能分类器中最低的，这个最低的错误率便是贝叶斯错误率。

因此，贝叶斯错误率不是一个可以随意降低的指标，而是由数据的真实分布（类条件概率密度） 和类别出现的天然比例（先验概率） 共同决定的理论极限。

🎯 贝叶斯错误率在机器学习中的核心价值

在实践中，理解贝叶斯错误率至关重要，它为我们分析模型性能提供了关键标尺。

1. 1. 性能评估的基准 ：它将模型总误差分解为两部分。可避免偏差 （模型误差与贝叶斯错误率之间的差距）和不可避免的误差（贝叶斯错误率本身）。这指导我们应该专注于减少"可避免偏差"。
2. 2. 问题固有难度的度量：一个人类专家识别错误率就有14%的嘈杂语音任务，其贝叶斯错误率至少为14%。这提醒我们，设定合理的性能预期很重要。
3. 3. 模型选择与改进的方向：如果模型错误率远高于估计的贝叶斯错误率，说明模型本身有较大改进空间（高偏差）。如果接近贝叶斯错误率，则优化重点应转向防止过拟合（高方差）或收集更本质的新特征。

为了更清晰，我们可以通过下表来对比不同误差概念：

误差类型	定义	在模型优化中的意义
贝叶斯错误率	任何分类器都无法避免的理论最低错误率	性能的终极极限，用于定义"可避免偏差"
人类水平误差	人类专家在该任务上的表现	常作为贝叶斯错误率的实用近似或上界
训练误差	模型在训练数据上的错误率	衡量模型对训练数据的拟合程度
测试误差	模型在未见过数据上的错误率	衡量模型的泛化能力，是我们优化的最终目标

🔬 如何估计贝叶斯错误率？

精确计算贝叶斯错误率需要知道数据的真实概率分布，这在实际中几乎不可能。因此，研究人员发展出多种估计方法：

• • 利用人类水平性能 ：在很多任务（如图像识别、语音转录）中，人类专家的错误率可以作为贝叶斯错误率一个很好的近似上界。

• • 理论推导与模拟：若假设数据服从已知分布（如高斯分布），则可直接积分计算理论BER。下文代码示例将展示这一点。

• • 基于散度的边界估计 ：这是学术研究的前沿。例如，通过计算类别分布之间的Henze-Penrose (HP) 散度，可以推导出贝叶斯错误率的上界。近年来，研究者提出了计算效率更高的广义HP散度估计方法，以应对多类别、大数据集的情况。

💻 Python示例：理论计算与估计

以下示例演示了在已知数据分布的理想情况下，如何计算理论贝叶斯错误率，并与实际分类器（高斯朴素贝叶斯）的性能进行比较。

import numpy as np
from scipy.stats import norm
from scipy.integrate import quad
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 1. 设定已知的数据分布参数（模拟两个类别）
# 假设两个类别的特征都服从正态分布，且先验概率相等
mean1, std1 = 0.0, 1.0   # 类别1的均值和标准差
mean2, std2 = 2.0, 1.5   # 类别2的均值和标准差
prior1 = prior2 = 0.5     # 先验概率

# 2. 理论计算贝叶斯错误率（通过数值积分）
# 贝叶斯决策边界是使得 posterior1 = posterior2 的点
# 即：prior1 * pdf1(x) = prior2 * pdf2(x)
# 由于先验相同，等价于找 pdf1(x) = pdf2(x) 的点，这里存在一个解析解，但我们演示数值方法

defbayes_error_rate(x):
    # 对于给定的点x，最优决策会选择概率密度更大的类别
    # 错误发生在：真实类别是1但pdf2>pdf1，或真实类别是2但pdf1>pdf2
    p1 = prior1 * norm.pdf(x, mean1, std1)
    p2 = prior2 * norm.pdf(x, mean2, std2)
    # 最小错误是选择概率大的那个，所以错误部分是概率小的那个
    returnmin(p1, p2)

# 在足够宽的区间上积分，计算总错误率
theory_ber, _ = quad(bayes_error_rate, -np.inf, np.inf)
print(f"理论贝叶斯错误率: {theory_ber:.4f} 或 {theory_ber*100:.2f}%")

# 3. 从该分布中生成样本数据，并用一个模型进行分类
np.random.seed(42)
n_samples = 10000
# 生成类别标签
y = np.random.binomial(1, prior2, n_samples)  # 1代表类别2，0代表类别1
# 根据类别生成特征
X = np.where(y == 0,
             norm.rvs(loc=mean1, scale=std1, size=n_samples),
             norm.rvs(loc=mean2, scale=std2, size=n_samples))
X = X.reshape(-1, 1)  # 转换为二维数组以供sklearn使用

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 使用高斯朴素贝叶斯分类器（其假设与真实数据生成过程部分匹配）
model = GaussianNB()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
model_error = 1 - model.score(X_test, y_test)

print(f"高斯朴素贝叶斯模型在测试集上的错误率: {model_error:.4f} 或 {model_error*100:.2f}%")
print(f"模型错误率与理论极限的差距: {(model_error - theory_ber):.4f}")

# 4. 可视化：绘制分布和决策边界（可选绘图部分）
x_plot = np.linspace(-5, 7, 1000)
pdf1 = prior1 * norm.pdf(x_plot, mean1, std1)
pdf2 = prior2 * norm.pdf(x_plot, mean2, std2)

plt.figure(figsize=(10, 6))
plt.plot(x_plot, pdf1, label=f'类别 1: N({mean1},{std1})', linewidth=2)
plt.plot(x_plot, pdf2, label=f'类别 2: N({mean2},{std2})', linewidth=2)
plt.fill_between(x_plot, np.minimum(pdf1, pdf2), 0, alpha=0.3, color='gray', label='贝叶斯错误区域')
plt.title('两类数据分布与贝叶斯错误区域')
plt.xlabel('特征值 x')
plt.ylabel('概率密度')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()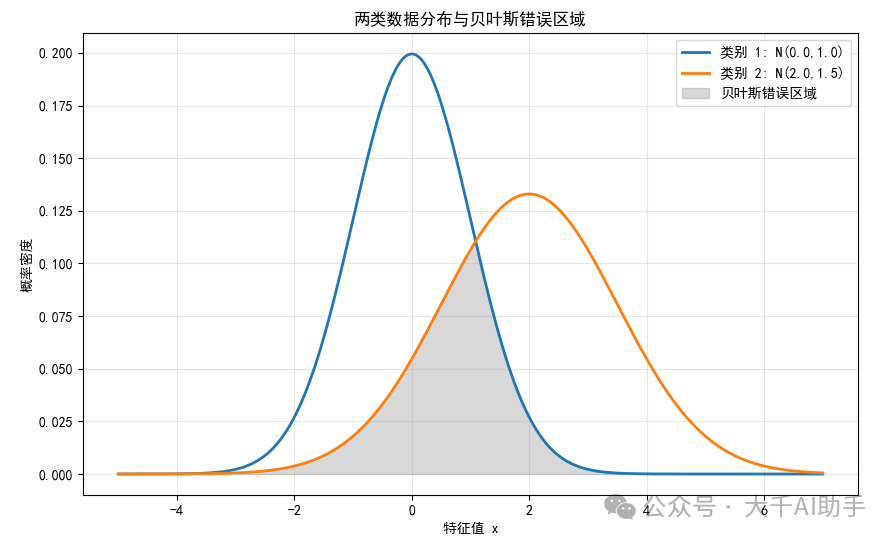

这段代码清晰地展示了：

1. 理论计算：在已知数据服从高斯分布的理想情况下，通过数值积分直接计算理论贝叶斯错误率。灰色填充区域直观展示了错误的来源------两类分布重叠的部分。

2. 实际对比 ：生成模拟数据，并训练一个分类器。你会观察到，即使是一个简单的模型，其错误率也无法低于理论计算的贝叶斯错误率。两者之间的差距，部分源于模型假设（如朴素贝叶斯假设特征独立）与数据真实生成过程的差异。

💎 Last

贝叶斯错误率是机器学习中一个深刻而优雅的概念，它像一座灯塔，为我们指明了模型性能改进的终极边界。理解它，能让我们：

• • 保持清醒：避免在已经逼近问题固有难度的任务上做无谓的优化。

• • 精准发力：将"可避免偏差"与"固有噪声"区分开，把资源和时间用在最能提升模型性能的地方。

• • 科学评估：为模型性能提供一个根本性的评估基准，而不仅仅是与其他模型进行横向对比。

尽管精确的贝叶斯错误率通常未知，但通过人类水平估计、理论分析或先进的边界估计方法逼近它，是每一个严谨的机器学习实践者应该具备的思维习惯。🚀

本文由「大千AI助手」原创发布，专注用真话讲AI，回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我，一起撕掉过度包装，学习真实的AI技术！