第四章 组合逻辑电路
-
数字电路分为两大类
- 组合逻辑电路 :任意时刻的输出仅仅取决于该时刻的输入组合,而与输入信号作用前电路的原状态无关(与过去的输入无关)。
- 时序逻辑电路 :任意时刻的输出不仅仅与该时刻的输入有关,而且还与电路的原状态有关(与过去的输入有关)。
-
组合逻辑电路的特点
- 电路由逻辑门构成,无记忆元件
- 输入信号是单向传输,一般无反馈
4.1 组合逻辑电路的分析
-
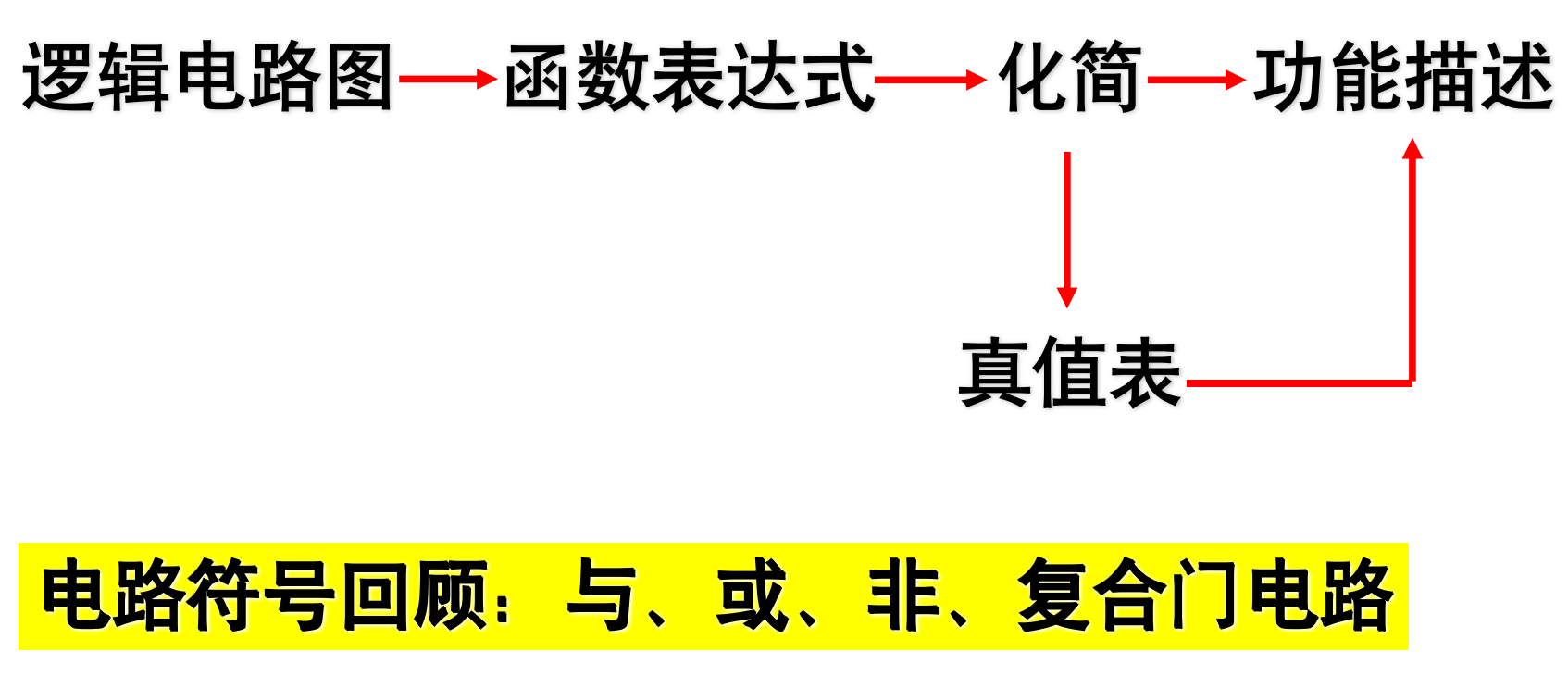
分析步骤:
-
注意:若化简完无法直接判断电路作用,一定要画真值表来分析电路作用
-
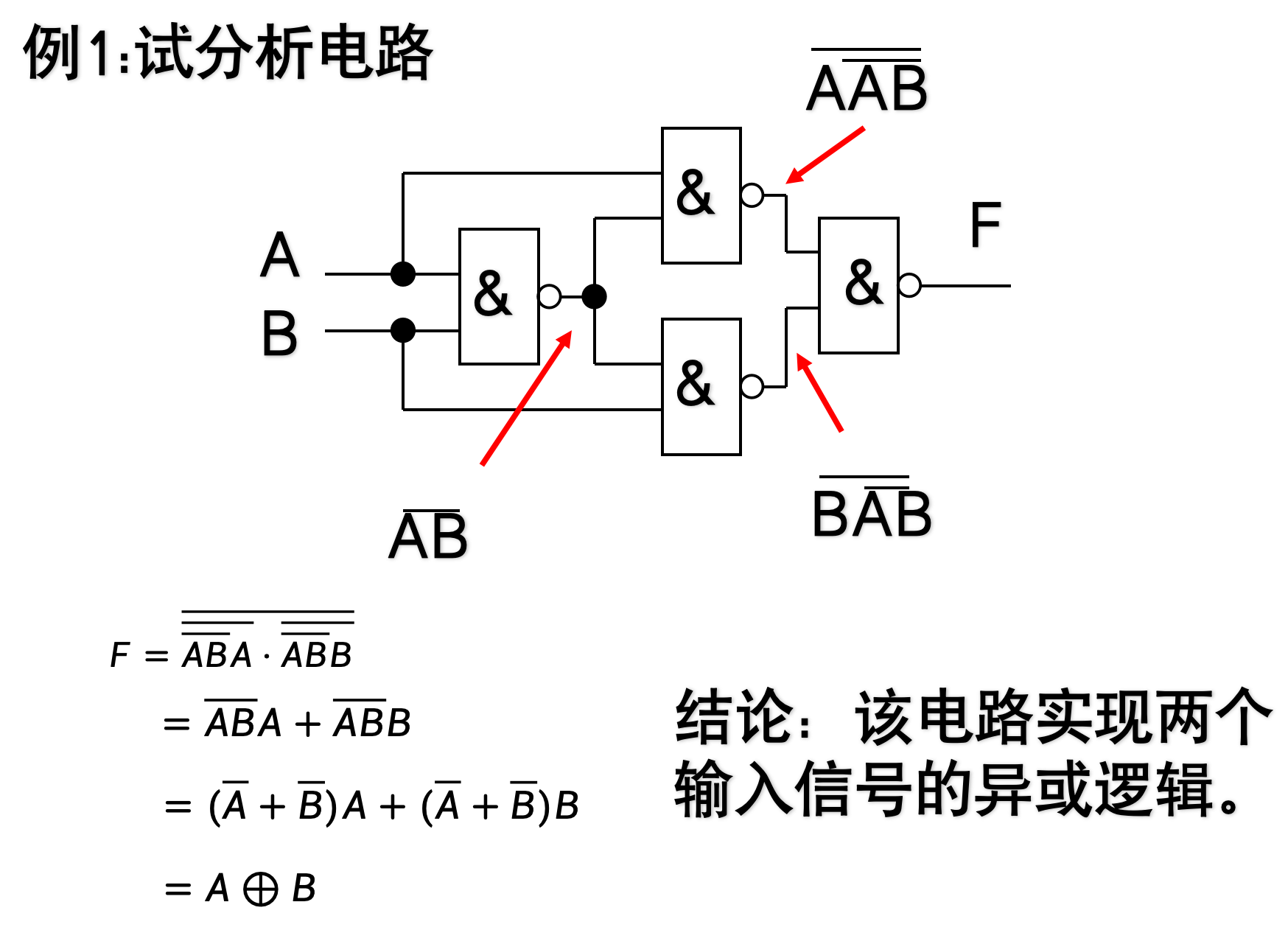
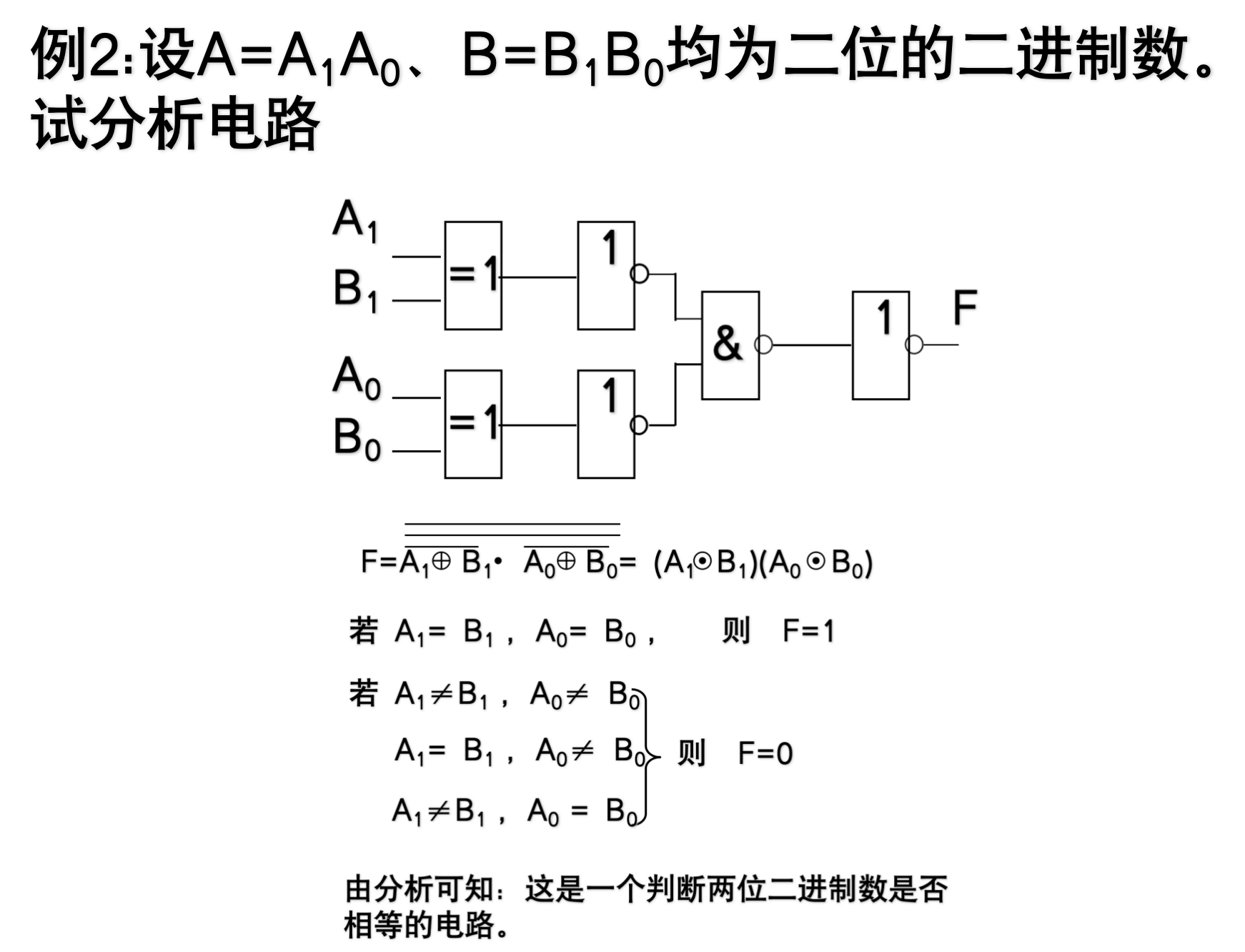
示例:
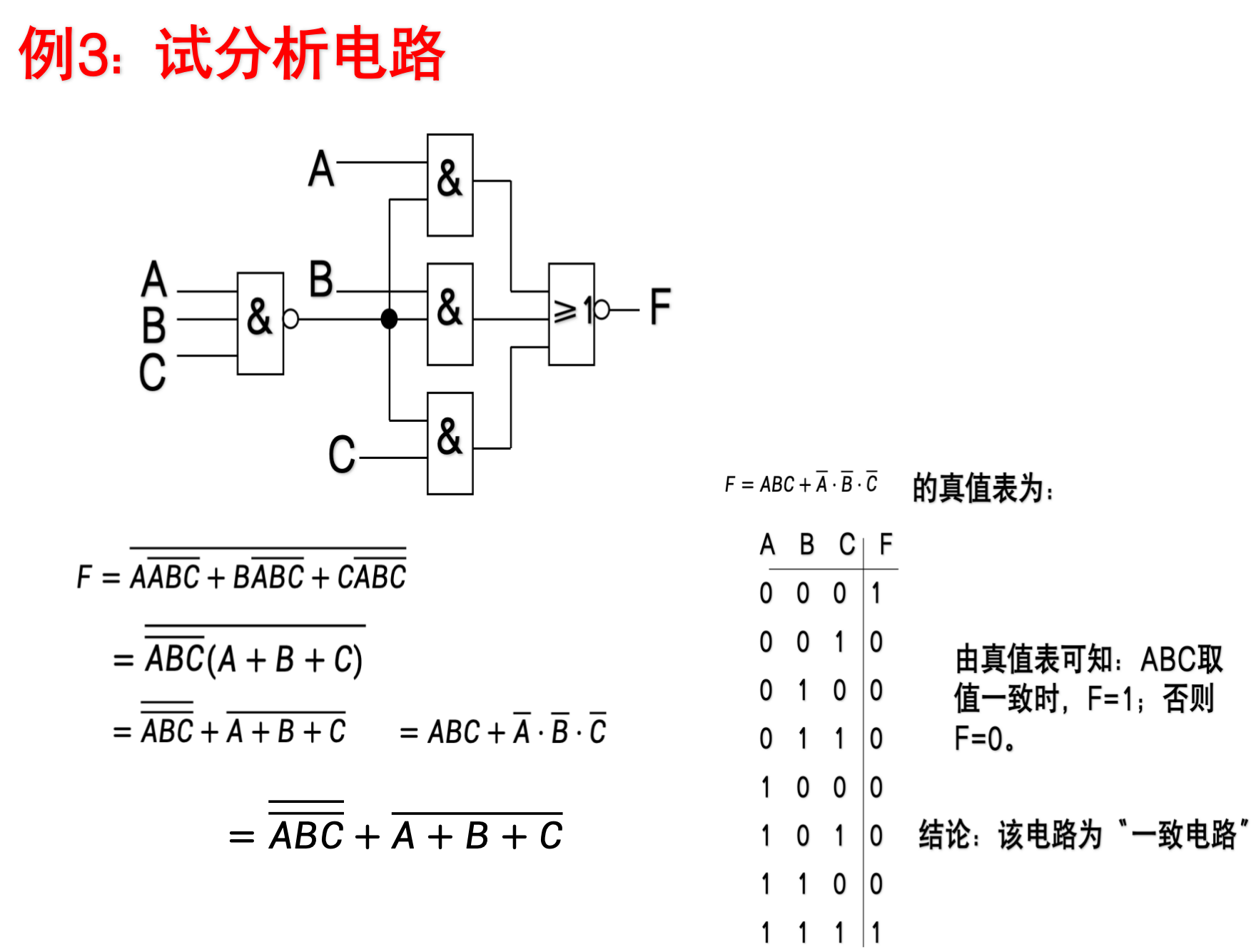
-
4.2 组合逻辑电路的设计
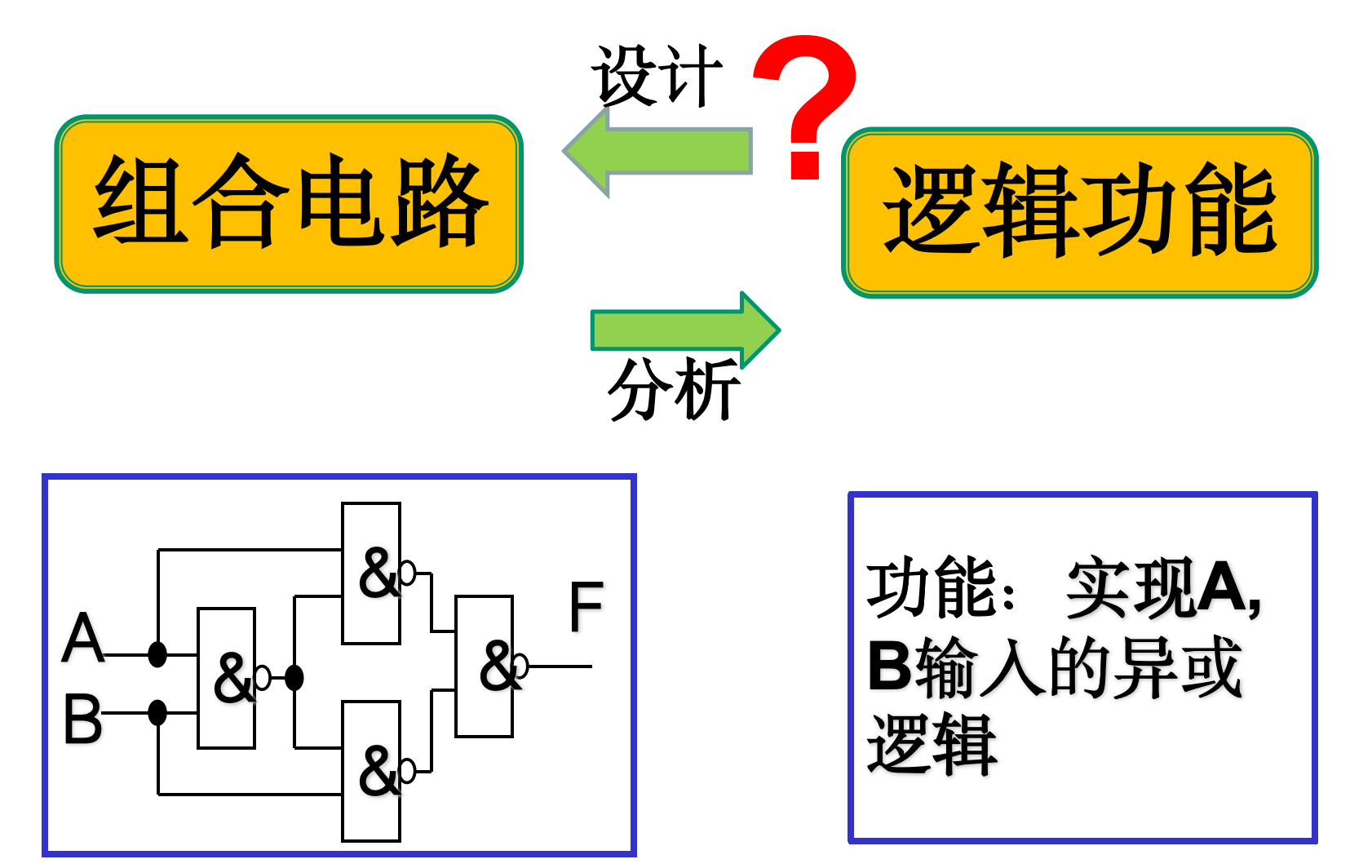
-
设计步骤
- 逻辑抽象与赋值
- 分析事件的因果关系,确定输入变量和输出变量。
- 定义逻辑状态的含义,即以"0"、"1"分别表示输入和输出的不同状态。
- 列出真值表(根据因果关系)
- 导出表达式 or 卡诺图
- 化简或变换
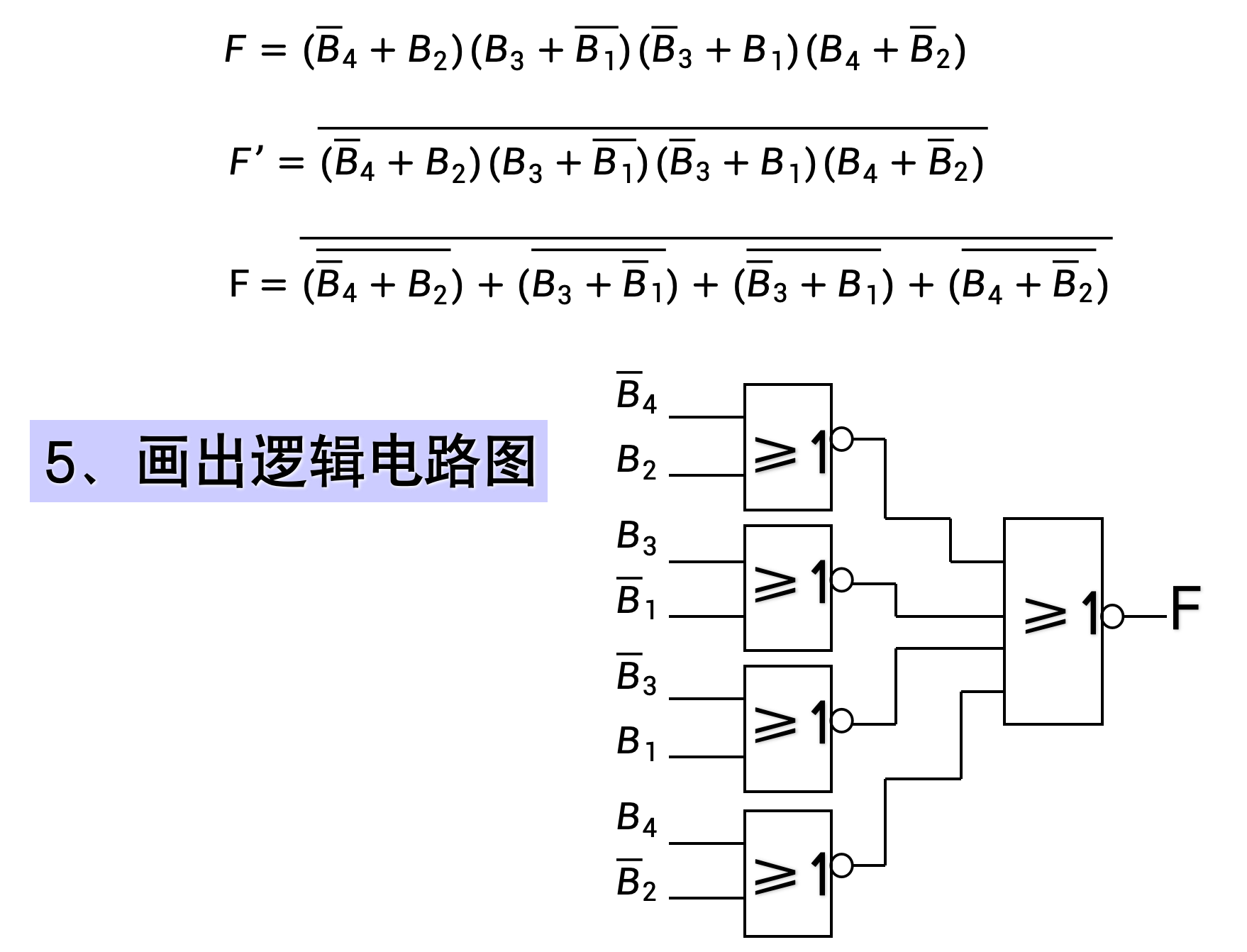
- 画出逻辑电路图
- 逻辑抽象与赋值
-
示例
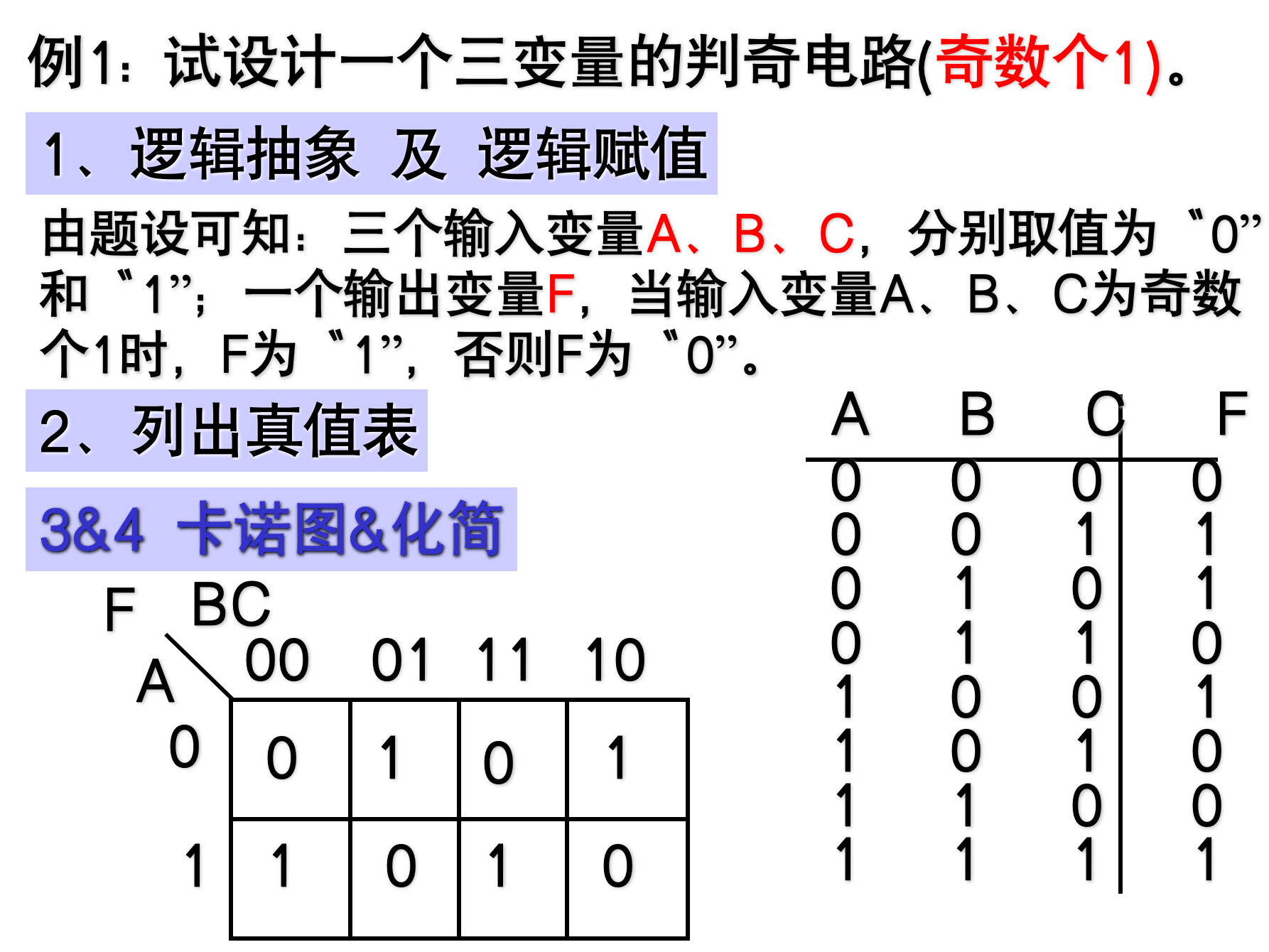
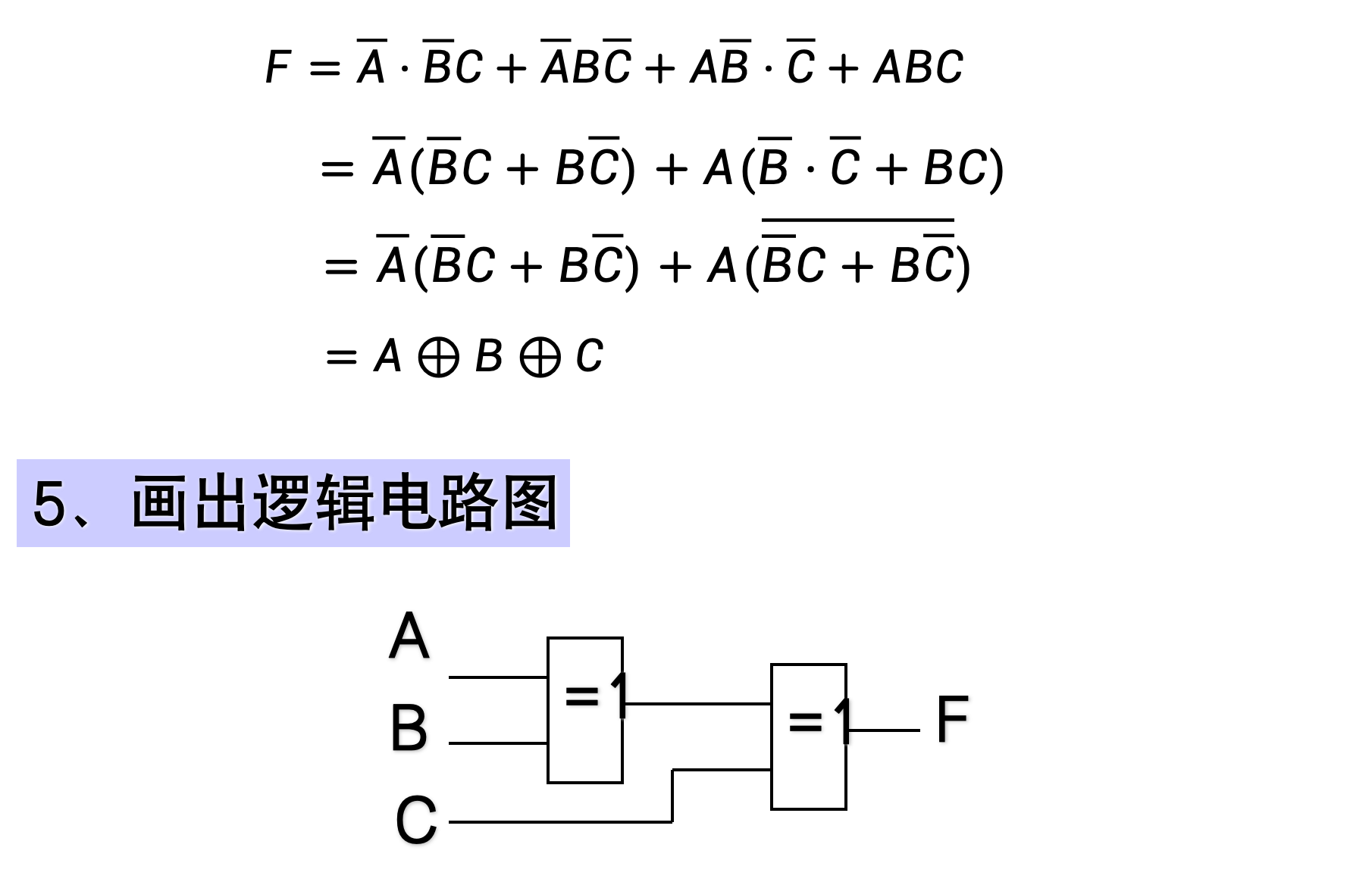

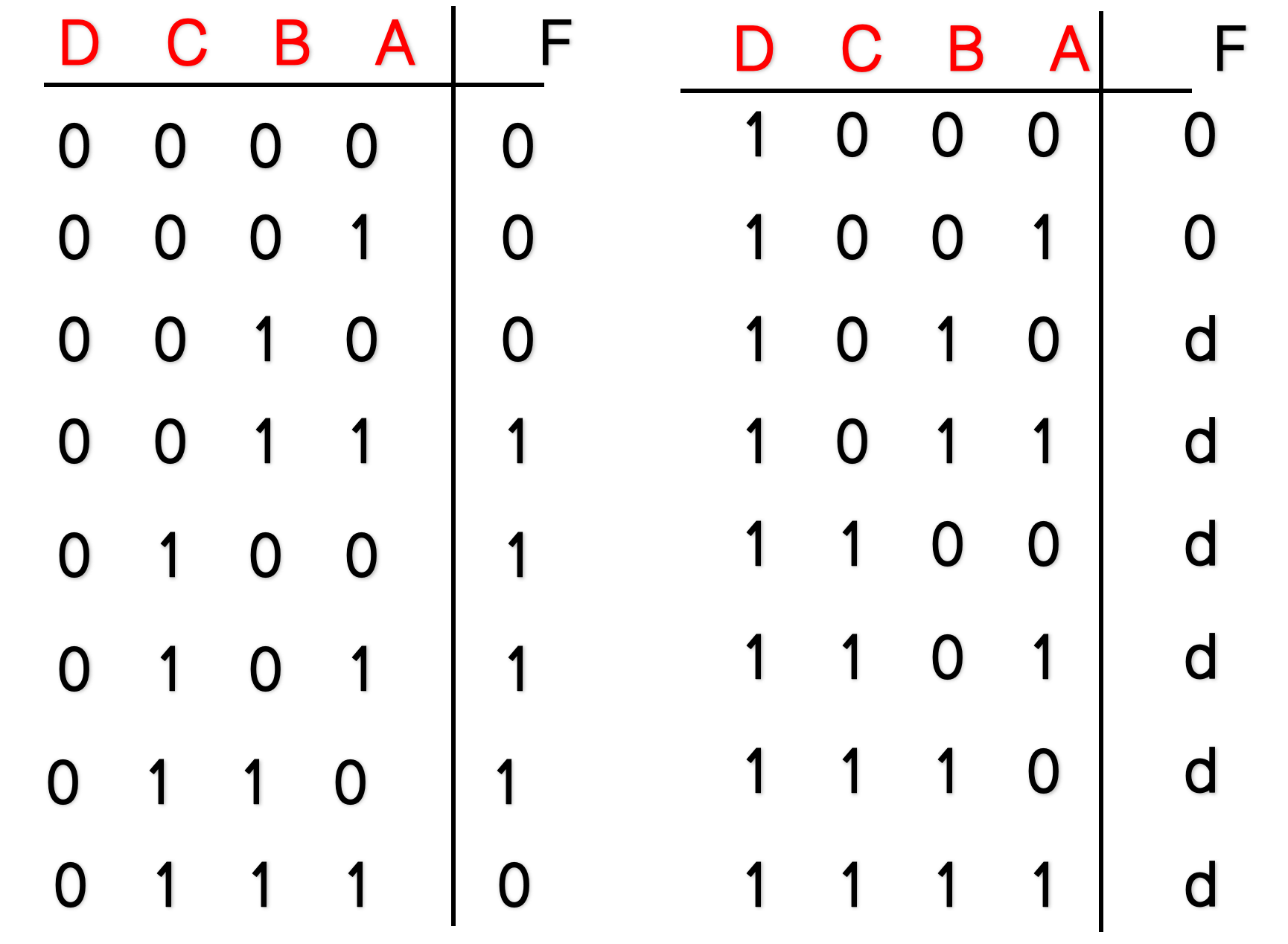
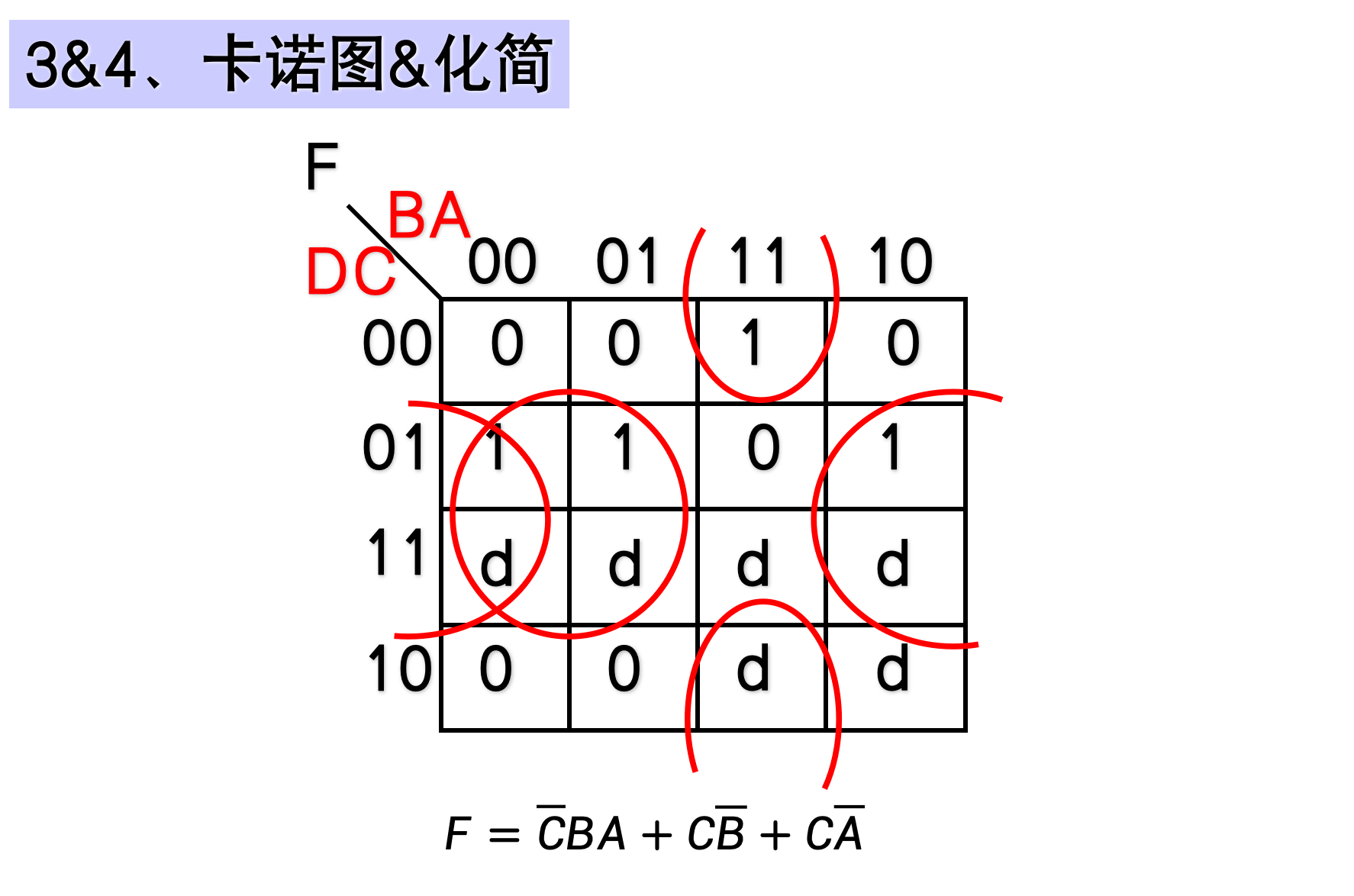
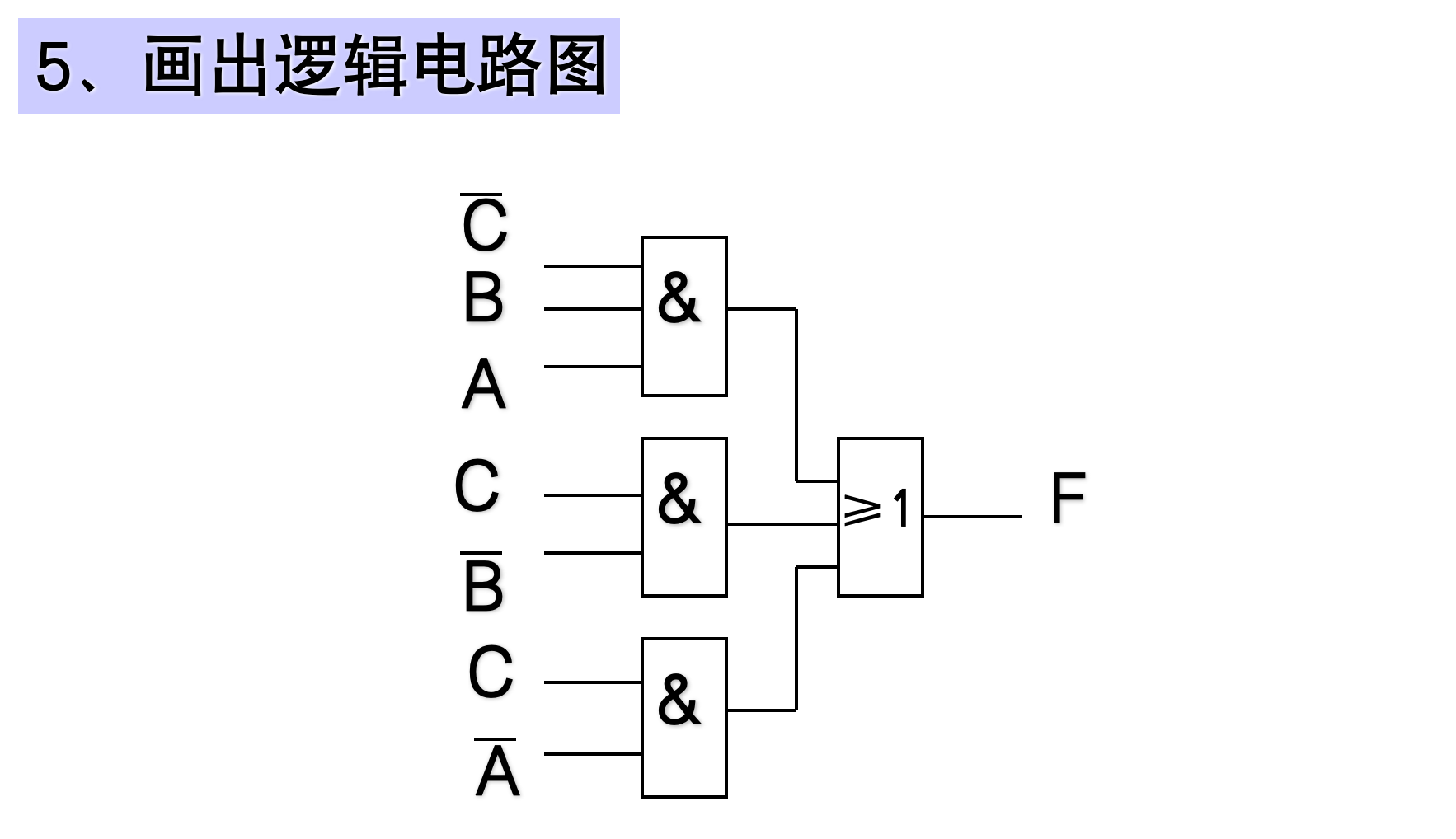

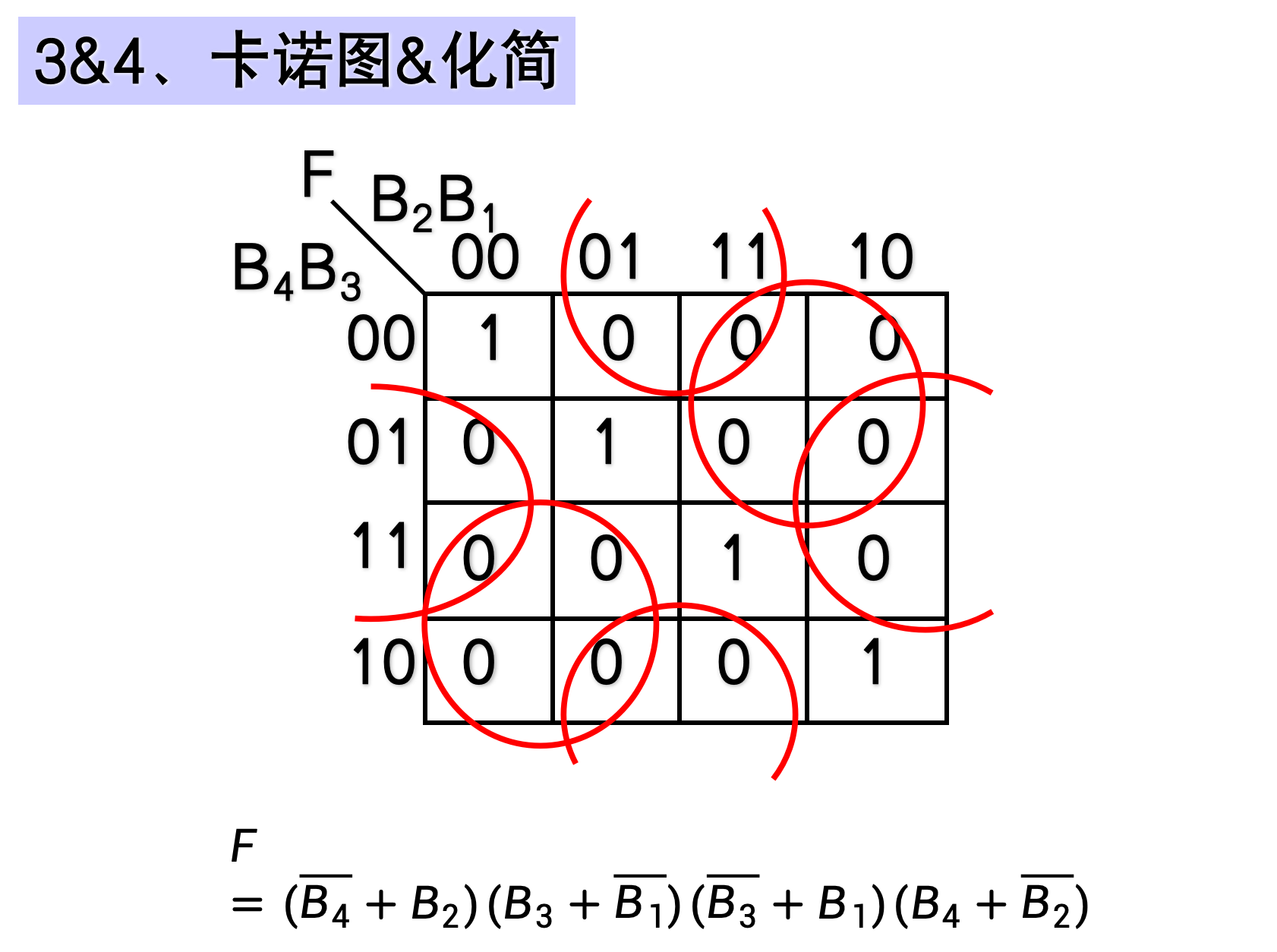
4.3 典型组合逻辑电路的设计
4.3.1 基本运算电路
4.3.1.1 半加器

-
数据流级描述方式
verilogmodule halfadd (a, b, c, s); input wire a, b; output wire c, s; assign c = a&b; assign s = a^b; endmodule
4.3.1.2 全加器
-
用逻辑门构成全加器
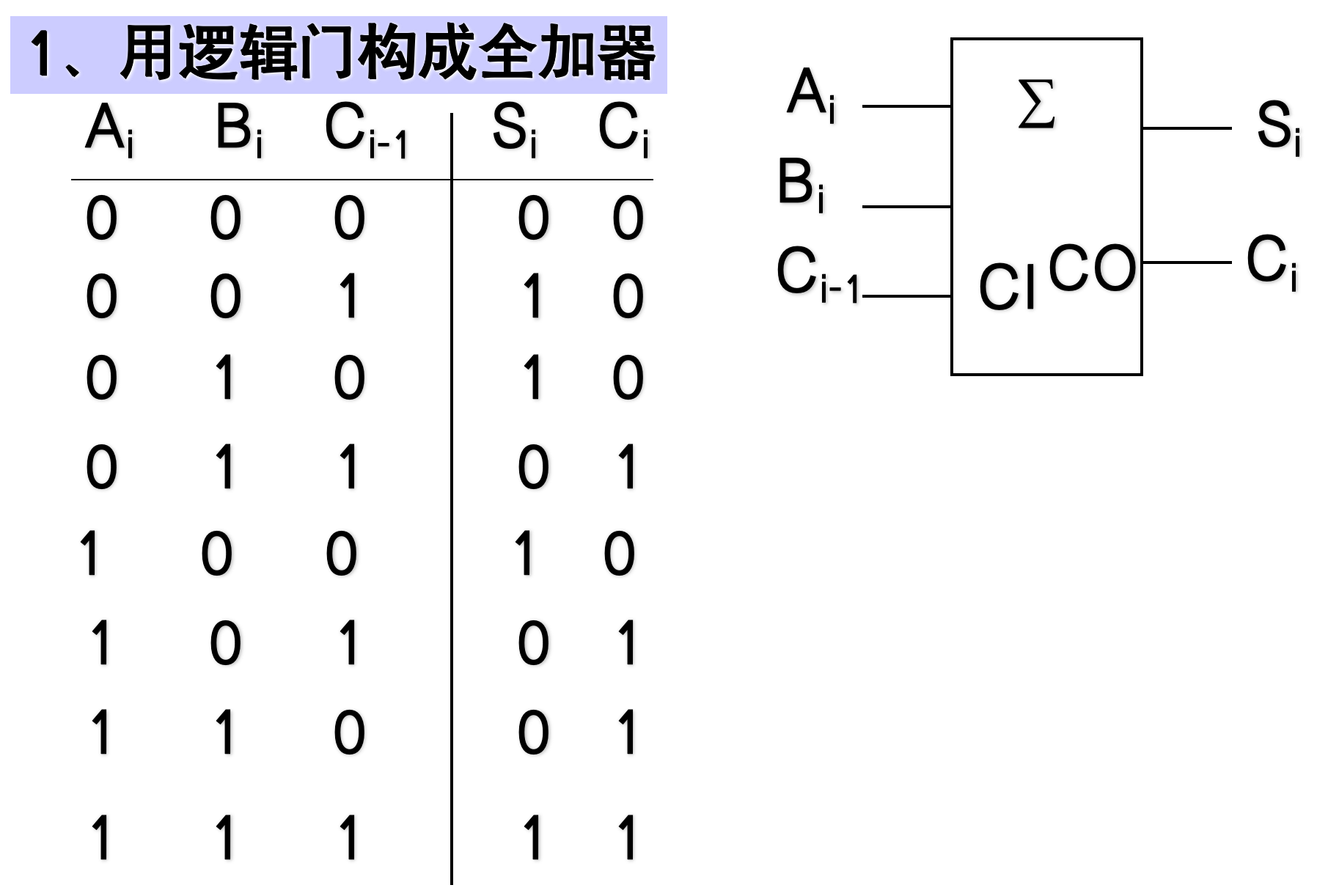
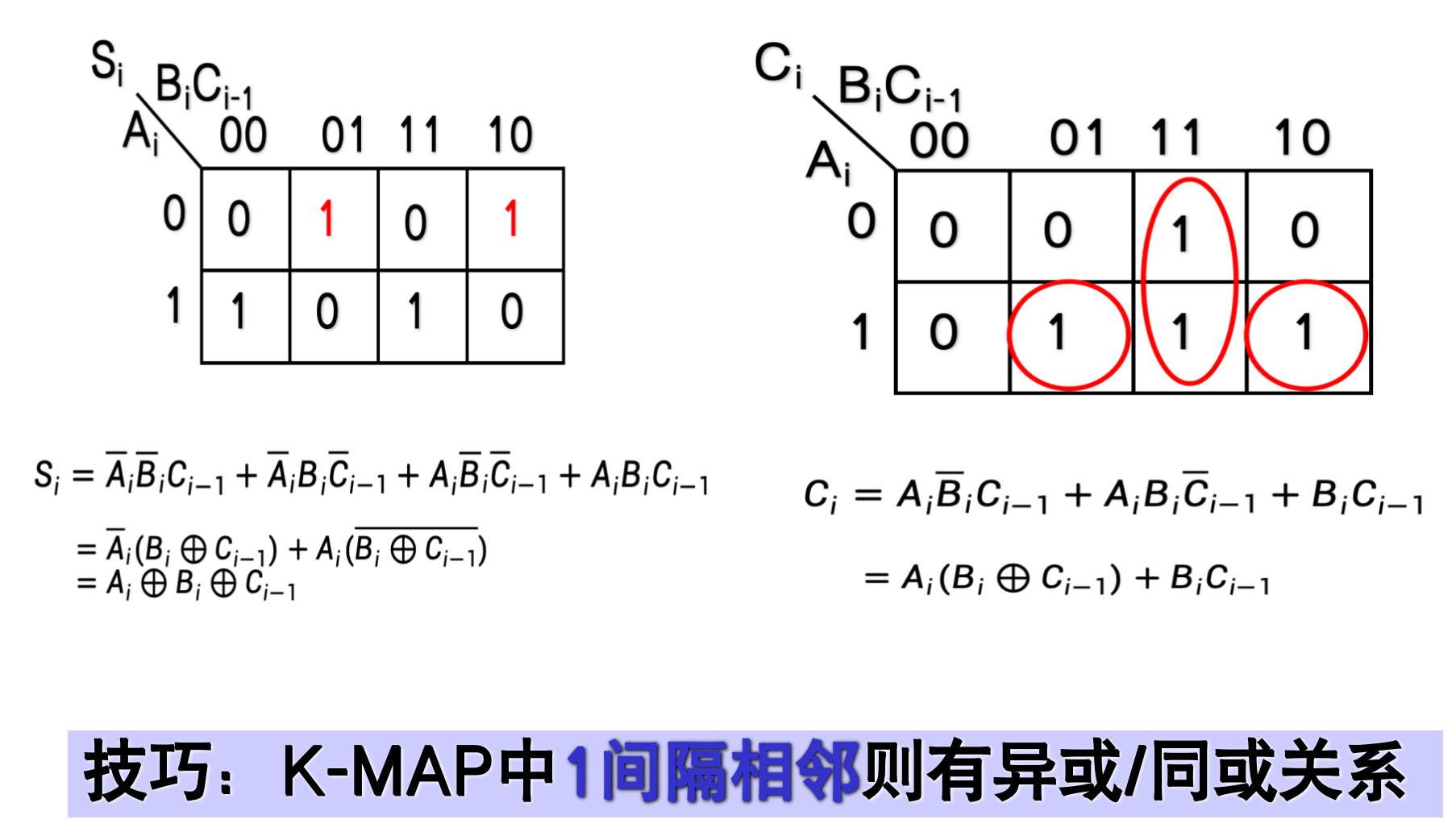
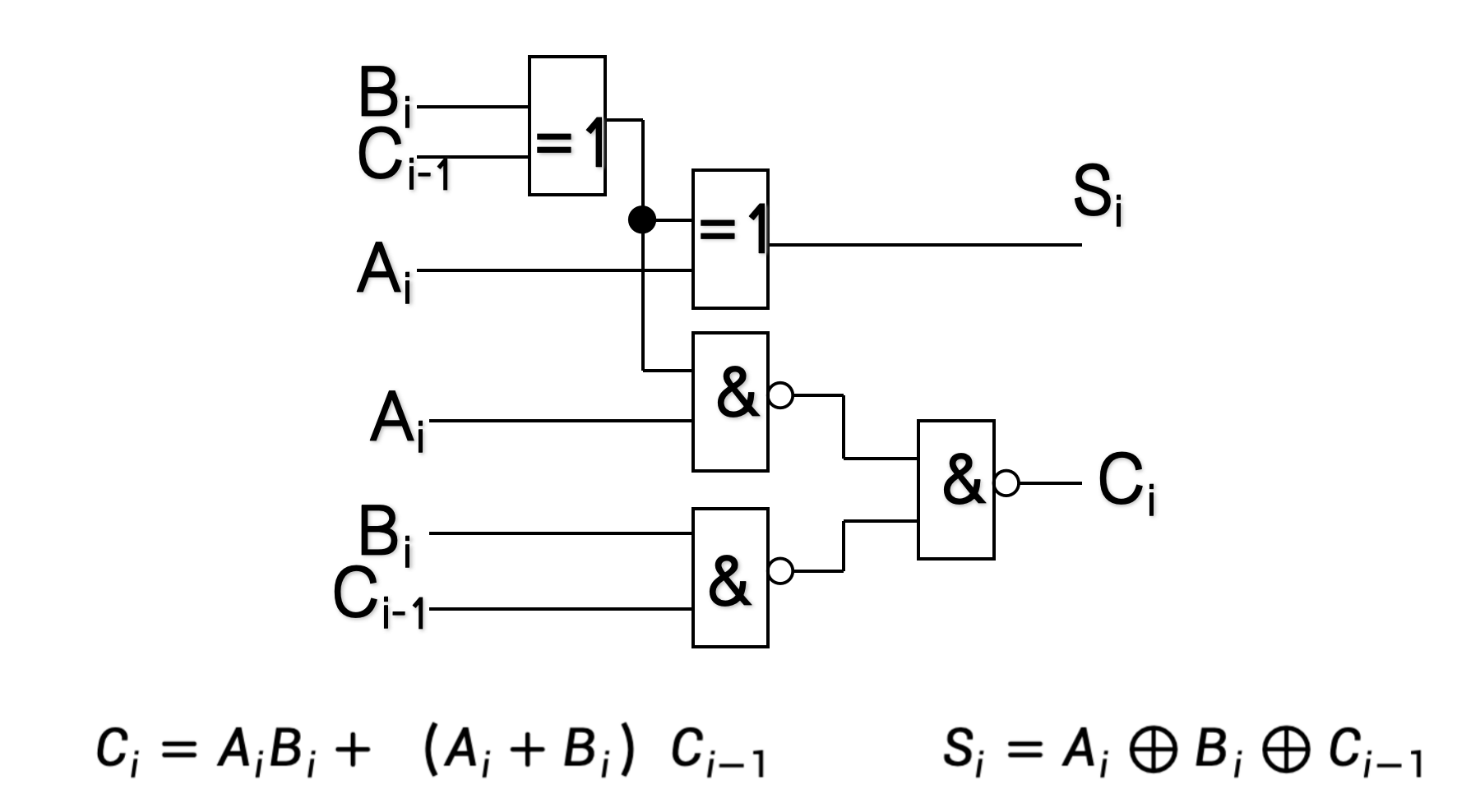
-
数据流级描述方式
verilogmodule adder (a, b, cl, ch, s); input wire a, b, cl; output wire ch, s; assign ch = (a&b) | ((a|b)&cl); assign s = a^b^cl; endmodule
-
-
集成全加器
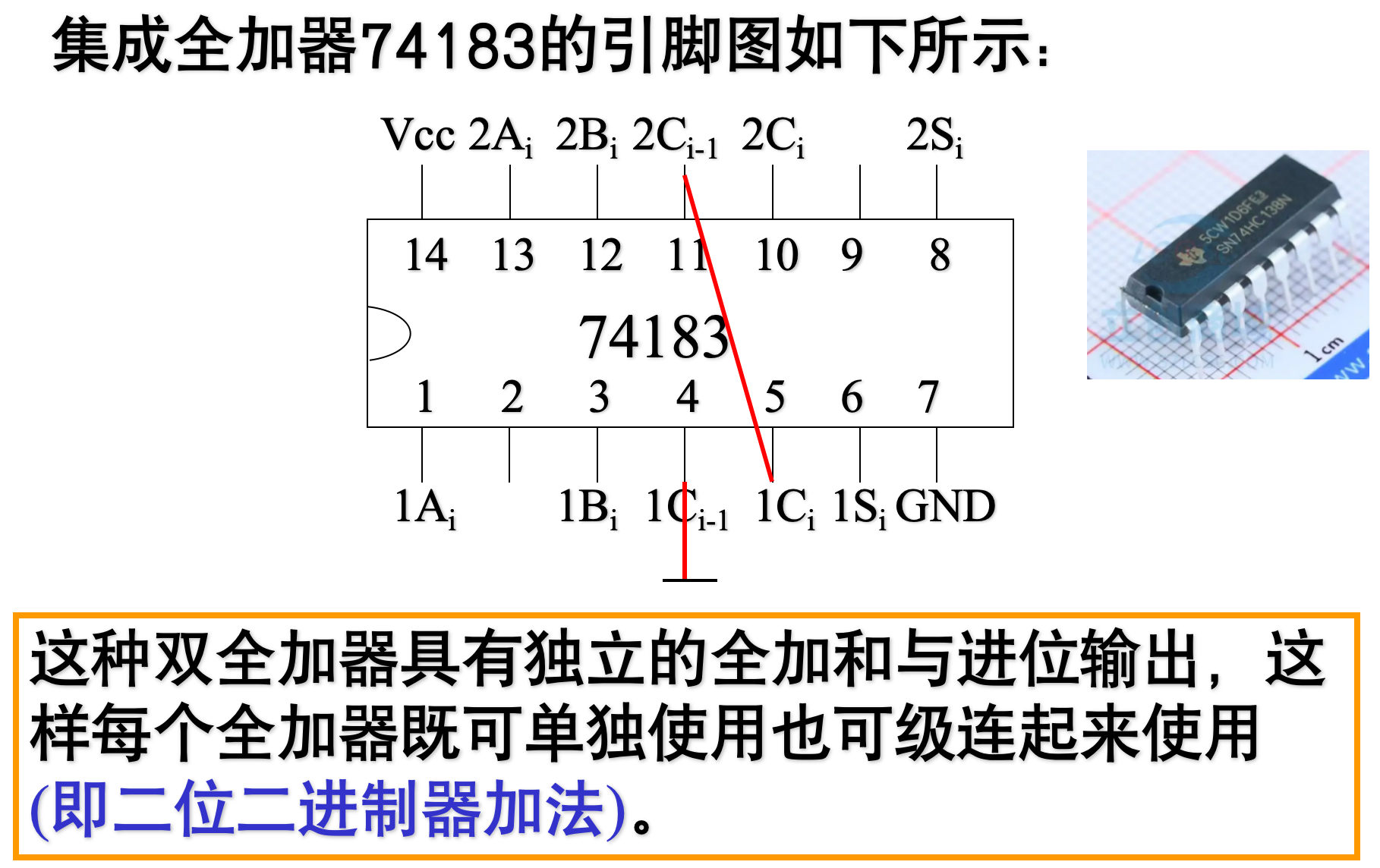

-
4位全加器-串行
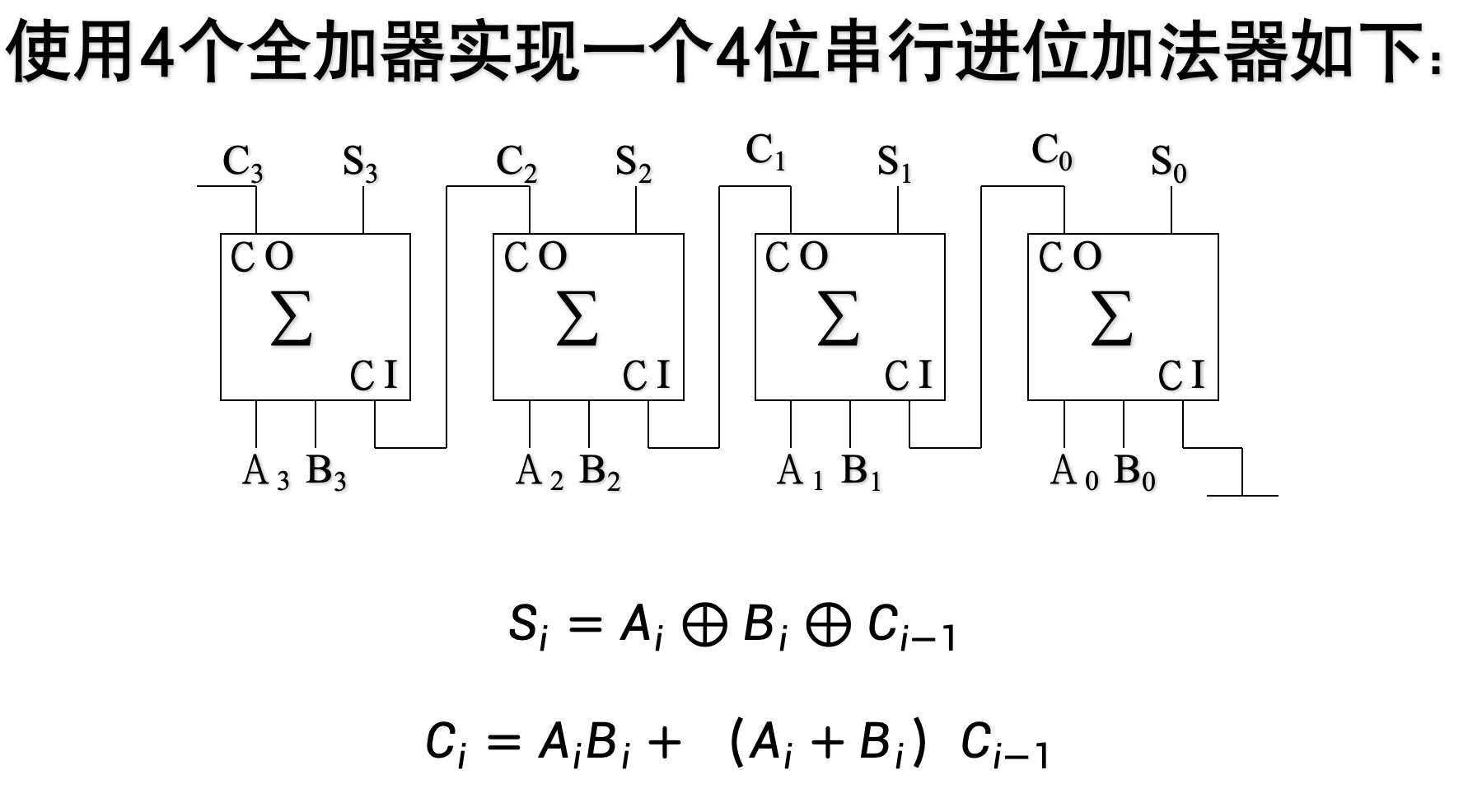
-
数据流级描述方式
verilogmodule adder4 (a, b, s, cf, ovf); input wire [3:0] a, b; output wire [3:0] s; output wire cf, ovf; /*ovf为溢出标记,定义为c[3]和c[4]的异或*/ wire [4:0] c; assign c[0] = 0; assign s[0] = a[0]^b[0]^c[0]; assign c[1] = a[0]&b[0] | (a[0]|b[0])&c[0]; assign s[1] = a[1]^b[1]^c[1]; assign c[2] = a[1]&b[1] | (a[1]|b[1])&c[1]; assign s[2] = a[2]^b[2]^c[2]; assign c[3] = a[2]&b[2] | (a[2]|b[2])&c[2]; assign s[3] = a[3]^b[3]^c[3]; assign c[4] = a[3]&b[3] | (a[3]|b[3])&c[3]; assign cf = c[4]; assign ovf = c[4]^c[3]; endmodule-
ps:溢出
- 溢出是对于有符号数来说的,对于无符号数不存在溢出的概念那么对于有符号数来说,什么情况会发生溢出?
- 两种:1、两个正数相加得到一个负数;2、两个负数相加得到一个正数
- 那么我们就对这两种情况来考虑,就看这个数的最高位和次高位,最高位就是符号位,次高位就是数值的最高位
- 1、对于两个正数相加时,一定是0X+0X,此时C4一定是0,那么如果C3是1,则S3为1,那么结果的最高位S3是符号位且为1,就是一个负数了,则C4=0,C3=1时,发生溢出;
- 2、对于两个负数相加时,一定是1X+1X,此时C4一定为1,那么如果C3为0,则S3位0,那么结果最高位S3是符号位且为0,就是一个正数了,则C4=1,C3=0时,发生溢出;
- 于是,综上两种情况,C3和C4如果一个为0一个为1,则发生溢出,可以用C4异或C3来实现
-
简化版代码

-
-
-
超前进位加法器



-
示例:



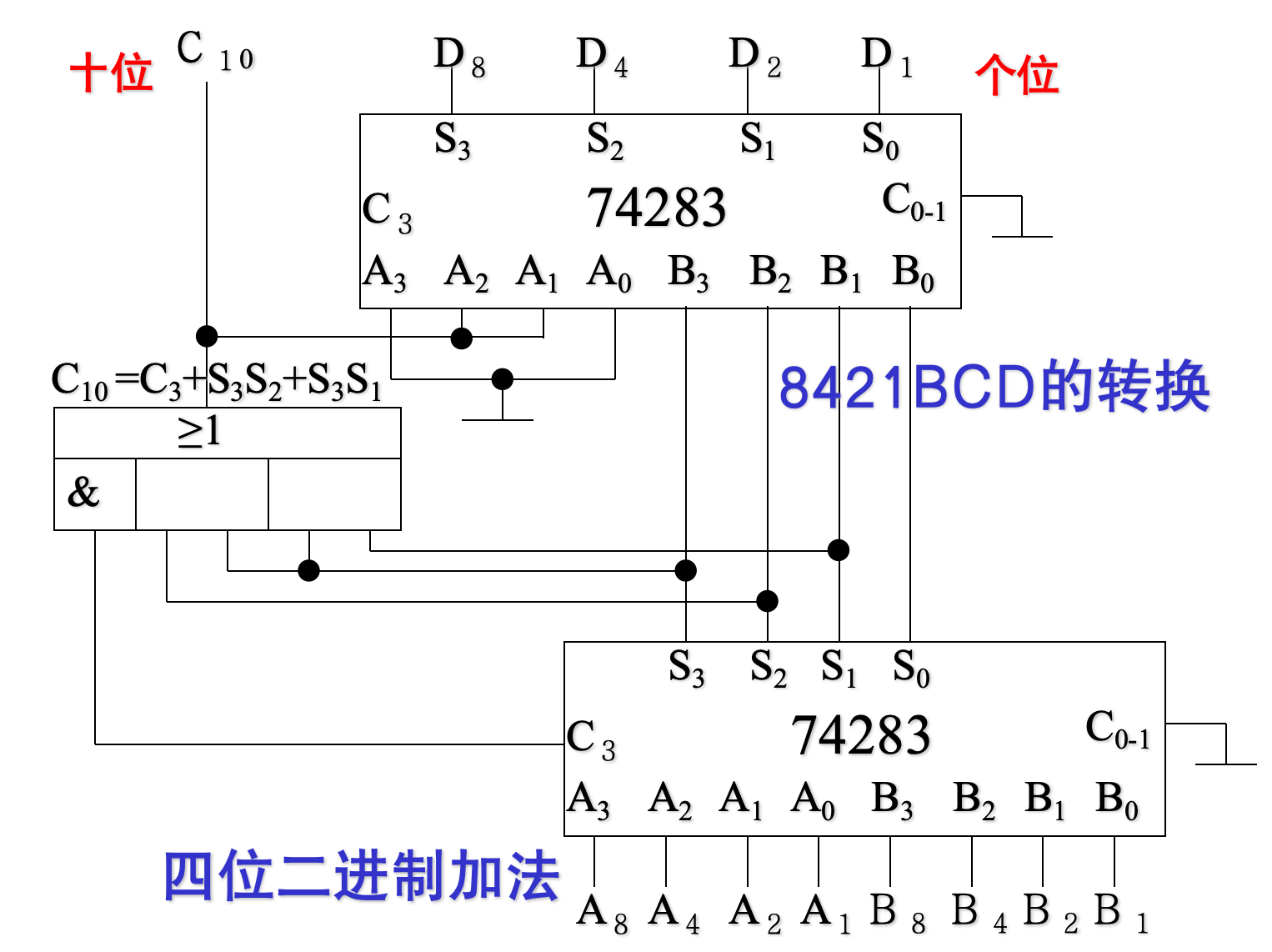
-
4.3.1.3 全减器
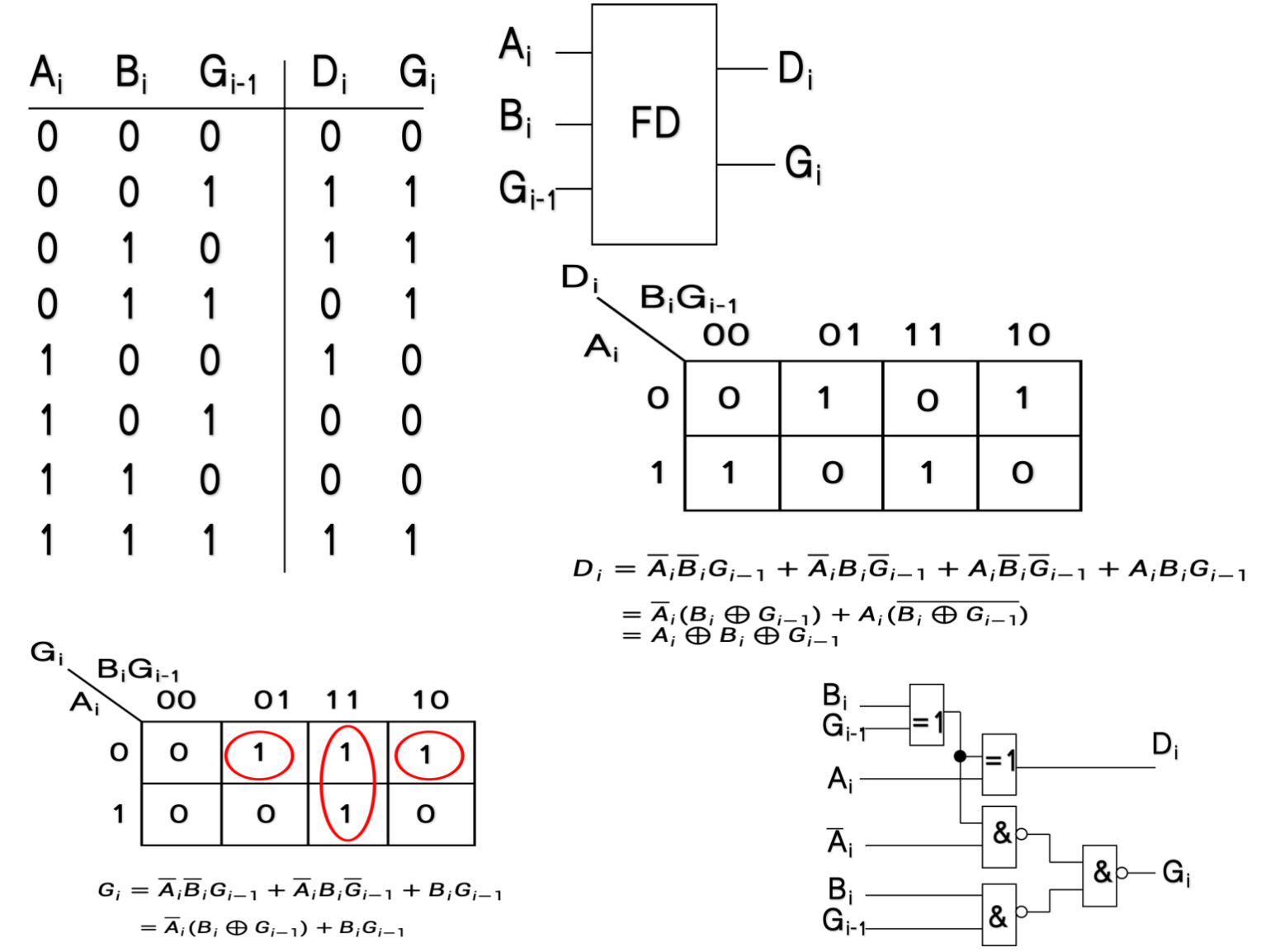

4.3.2 数值比较电路
4.3.2.1 一位比较电路

-
数据流级描述方式
verilogmodule comp1bit (a, b, gt, eq, lt); input wire a, b; output wire gt, eq, lt; assign gt = a&~b; assign eq = ~a&~b | a&b; assign lt = ~a&b; endmodule -
设计顶层文件
verilogmodule comp1bit_top ( input wire [1:0] sw, output wire [2:0] ld ); comp1bit U1 ( .a (sw[1]) , .b ( sw[0] ), .gt ( ld[2] ), .eq ( ld[1] ), .lt ( ld[0] ) ); endmodule
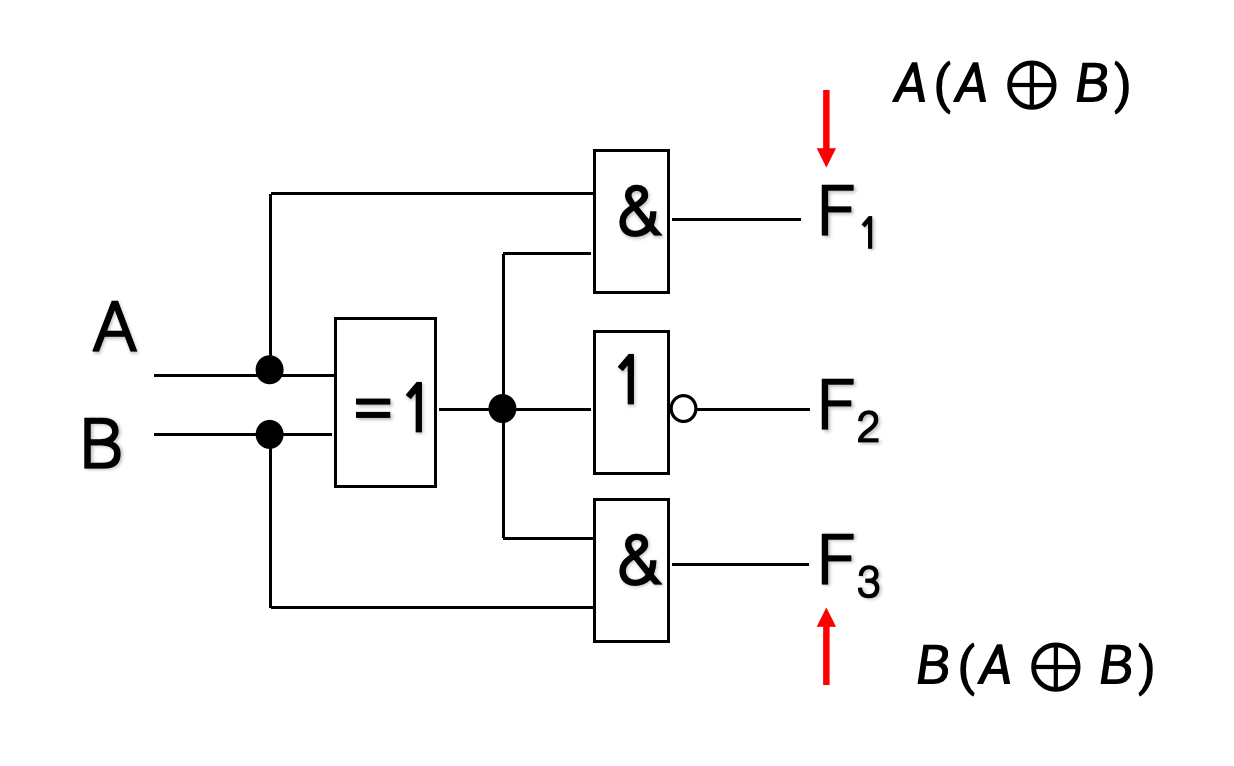
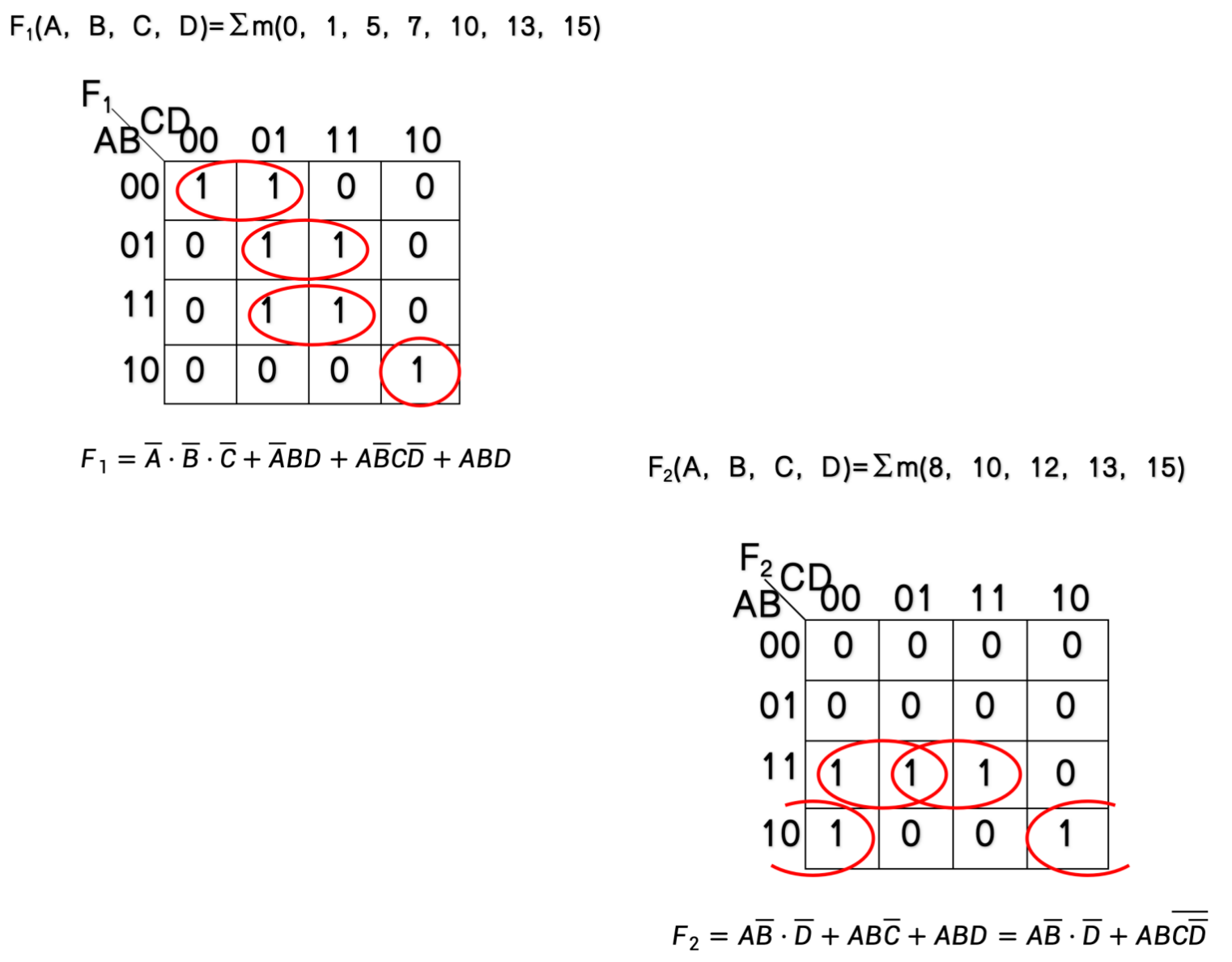
4.3.2.2 四位比较器
- 输入是 A = A 3 A 2 A 1 A 0 A = A_3 A_2 A_1 A_0 A=A3A2A1A0, B = B 3 B 2 B 1 B 0 B = B_3 B_2 B_1 B_0 B=B3B2B1B0
- F 1 F_1 F1对应 A > B A>B A>B 、 F 2 F_2 F2 对应 A = B A=B A=B 、 F 3 F_3 F3 对应 A < B A<B A<B



4.3.2.3 集成比较器的应用
-
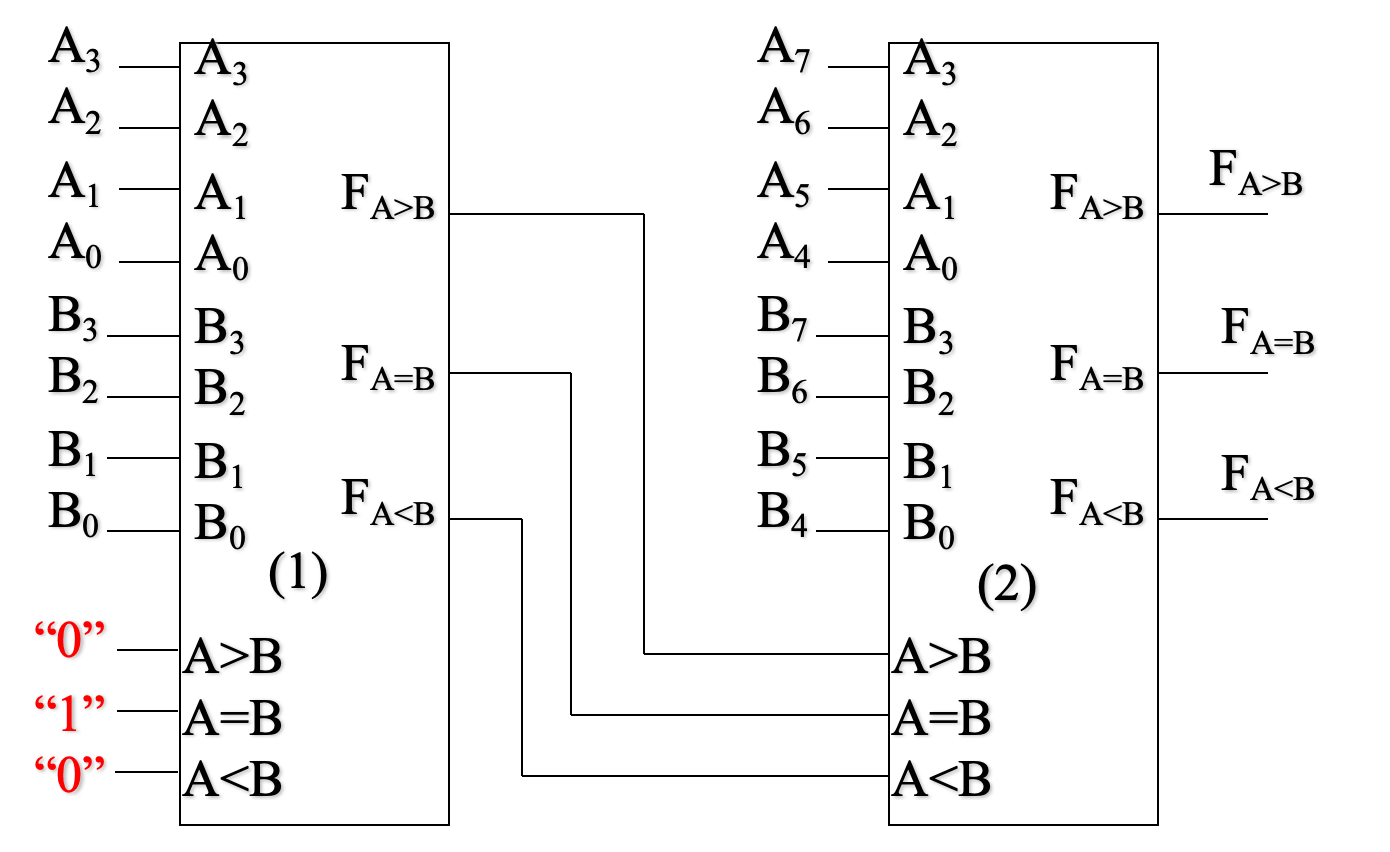
用7485构成8位二进制比较器
-
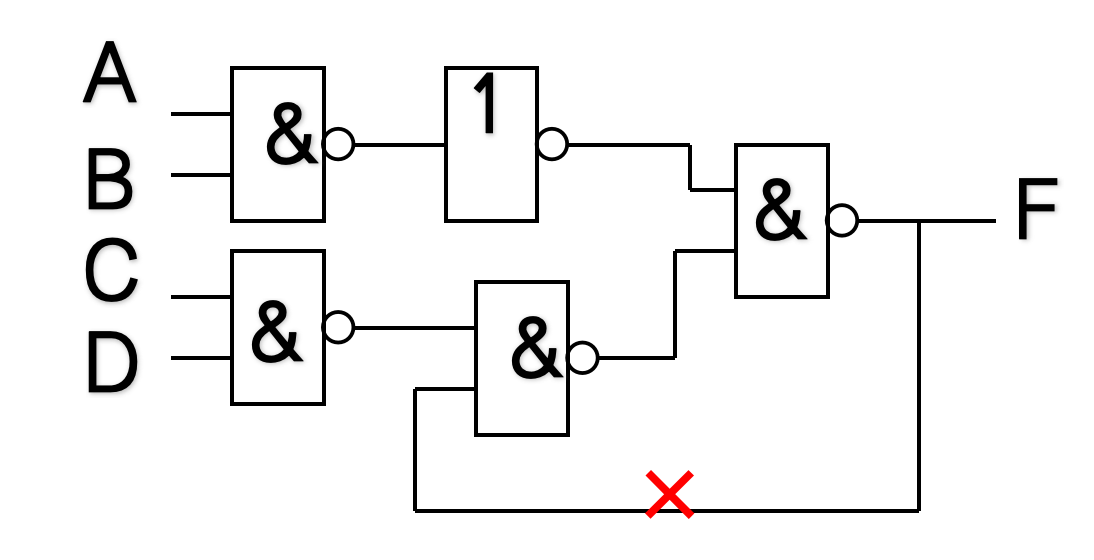
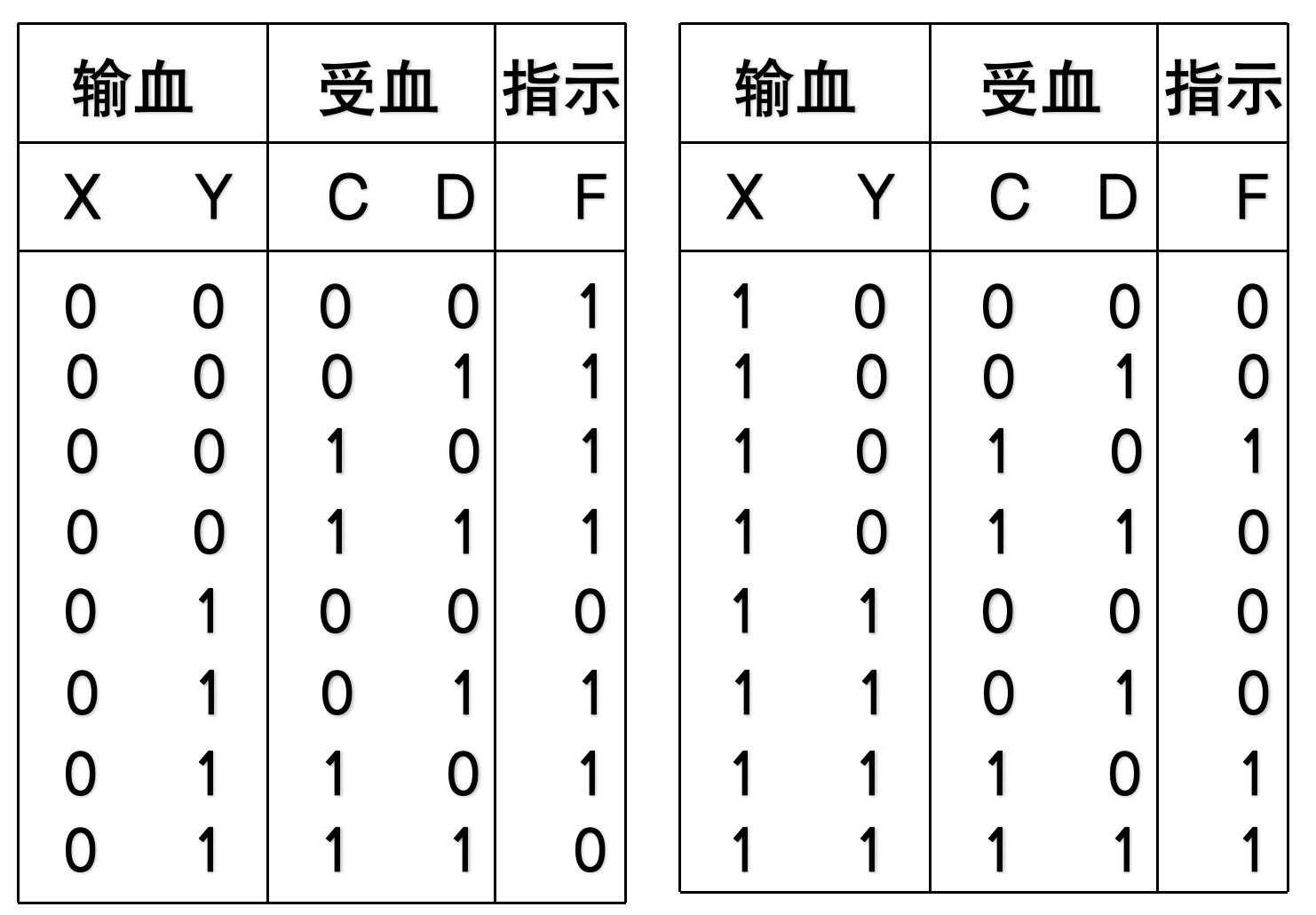
用7485和逻辑门设计输血指示器

-
根据输血常识,可输血的为以下三种:
- 只要血型相同就可以输,即XY=CD,则F=1;
- 只要输送的是O型血,即XY=00,则F=1;
- 只要接受方是AB型,即CD=10,则F=1;
- 其他情况均不可输血。
-
由此可得出:用4位数码比较器及门电路设计的输血指示器如下。

-
4.3.3 编码器
- 编码:是指用文字、符号和数码来表示某种信息的过程。
- 在数字系统中,由于采用二进制运算处理数据,因此通常将信息编成若干位二进制代码。
- 在逻辑电路中,信号都是以高、低电平的形式给出。
- 编码器:实现编码的数字电路,把输入的每个高低电平信号编成一组对应的二进制代码。
4.3.3.1 二进制编码器
-
二进制编码器:二进制编码的组合电路。
- 假设某编码器有n个输入端, I 0 , I 1 ... , I n − 1 I_0, I_1 ...,I_{n-1} I0,I1...,In−1 ,有m个输出端 Y 0 , Y 1 ... , Y m − 1 Y_0,Y_1 ...,Y_{m-1} Y0,Y1...,Ym−1 。
- 为了不使输出发生混乱而产生错误,普通编码器规定,在任何给定的时刻,n个输入端中只能有一个有效,其余n-1个都不能出现。
- 同时也可以知道,输入端的个数与输出端的个数有以下关系: 2 m ≥ n 2^m \geq n 2m≥n
- 输入是信号,输出是二进制编码
-
所谓编码,就是在选定的一系列二值代码中赋予每个代码以固定的含义。执行编码功能的电路称编码器。
-
二进制编码器 ------2 n 2^n 2n线-n线编码器
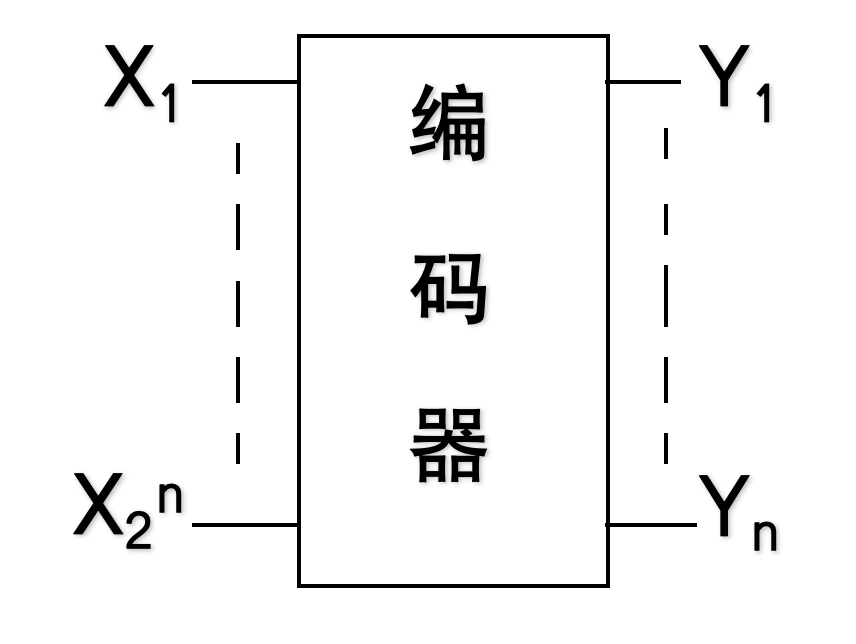
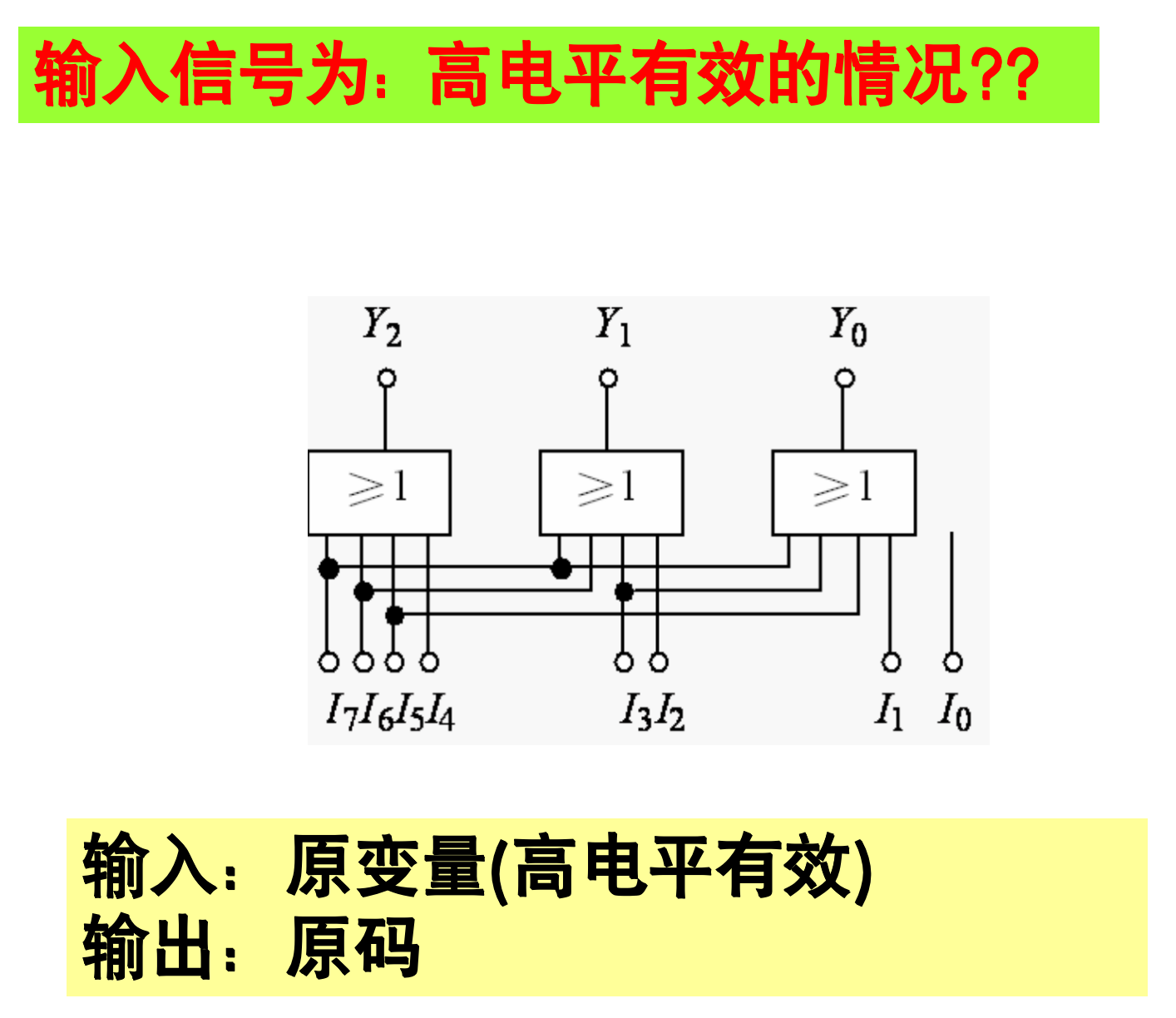
- 输入信号可以是低电平有效或高电平有效的形式
- 编码器的输出码可以是原码形式也可以是反码形式。
- 与十进制数数值对应的二进制码为原码。
- 把原码各位取反得到的码为反码。
-
4线-2线编码器
-
在数字系统中,经常需要对所处理的信息或数据赋予二进制代码,称为编码,用来完成编码工作的电路称为编码器。
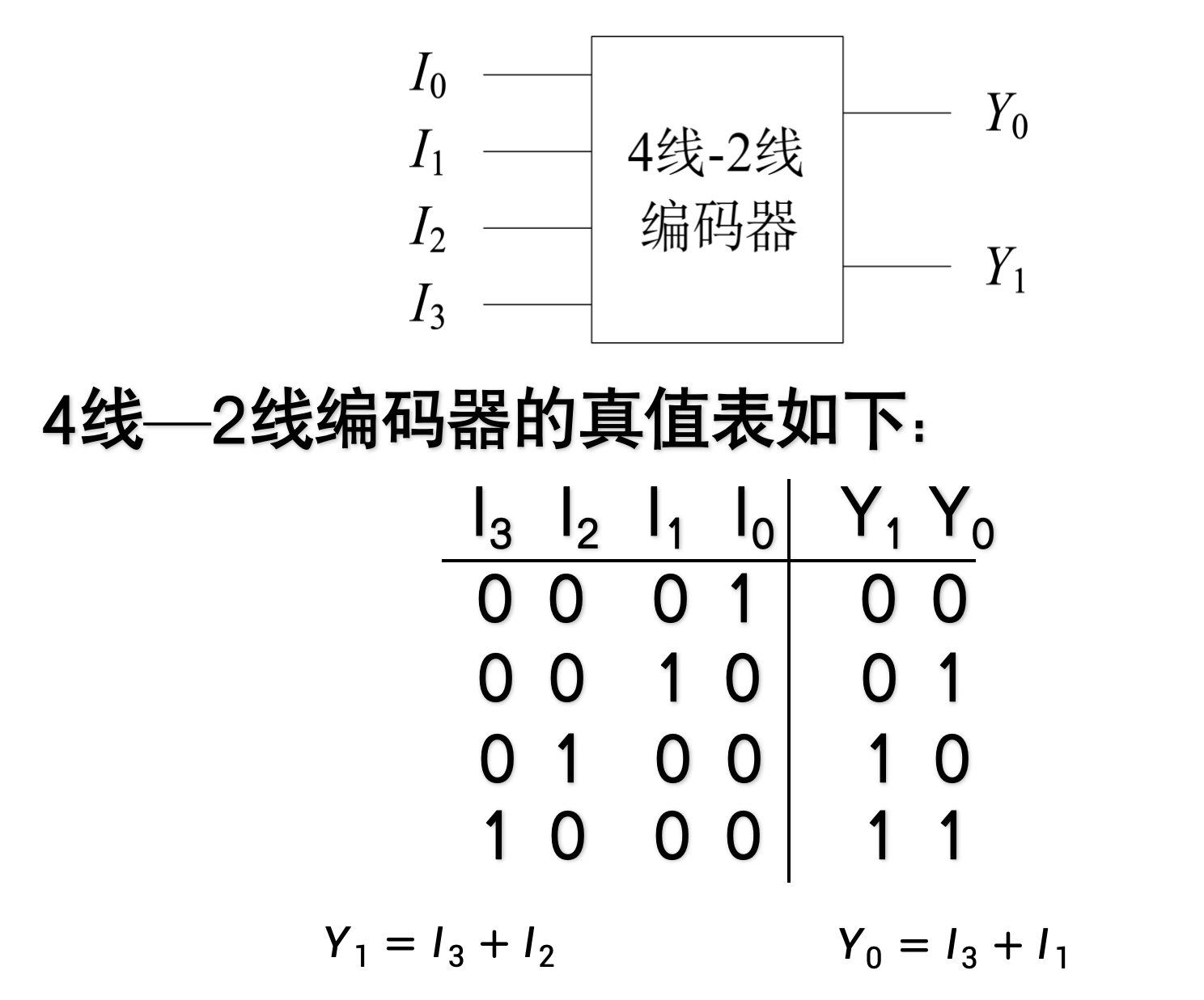
-
数据流级描述方式
verilogmodule ENC4_2a (i, y); input wire [3:0] i; output wire [1:0] y; assign y[0] = i[3]|i[1]; assign y[1] = i[3]|i[2]; endmodule -
行为级描述方式
verilogmodule ENC4_2a (i, y); input wire [3:0] i; output wire [1:0] y; always@(i): case(i) 4'b0001: y = 2'b00; 4'b0010: y = 2'b01; 4'b0100: y = 2'b10; 4'b1000: y = 2'b11; endcase endmodule -
顶层设计文件
verilogmodule ENC4_2a_top ( input wire [3:0] sw, output wire [1:0] ld ); ENC4_2a D1( .i(sw), .y(ld) ); endmodule
-
-
-
8线-3线编码器
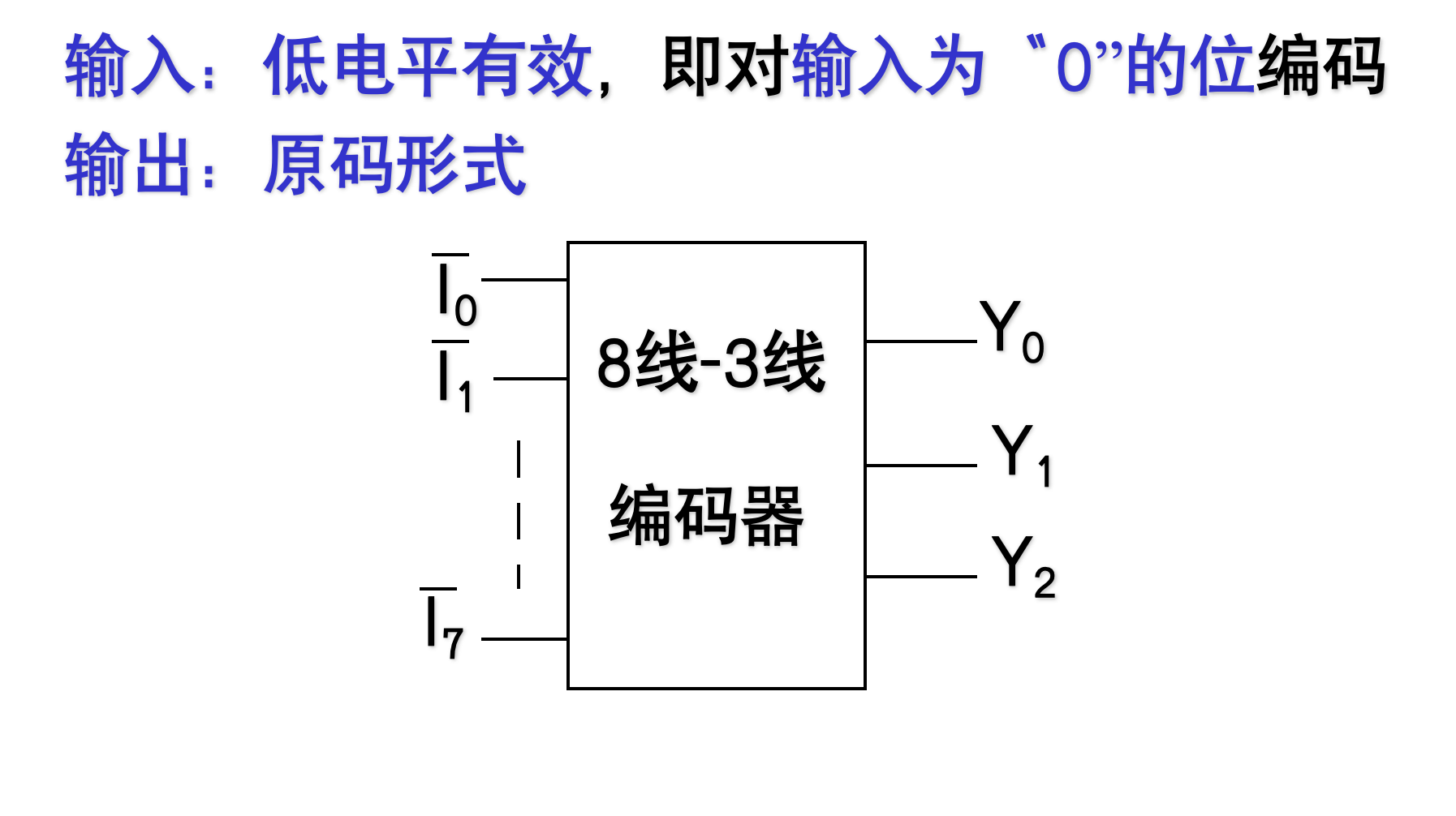
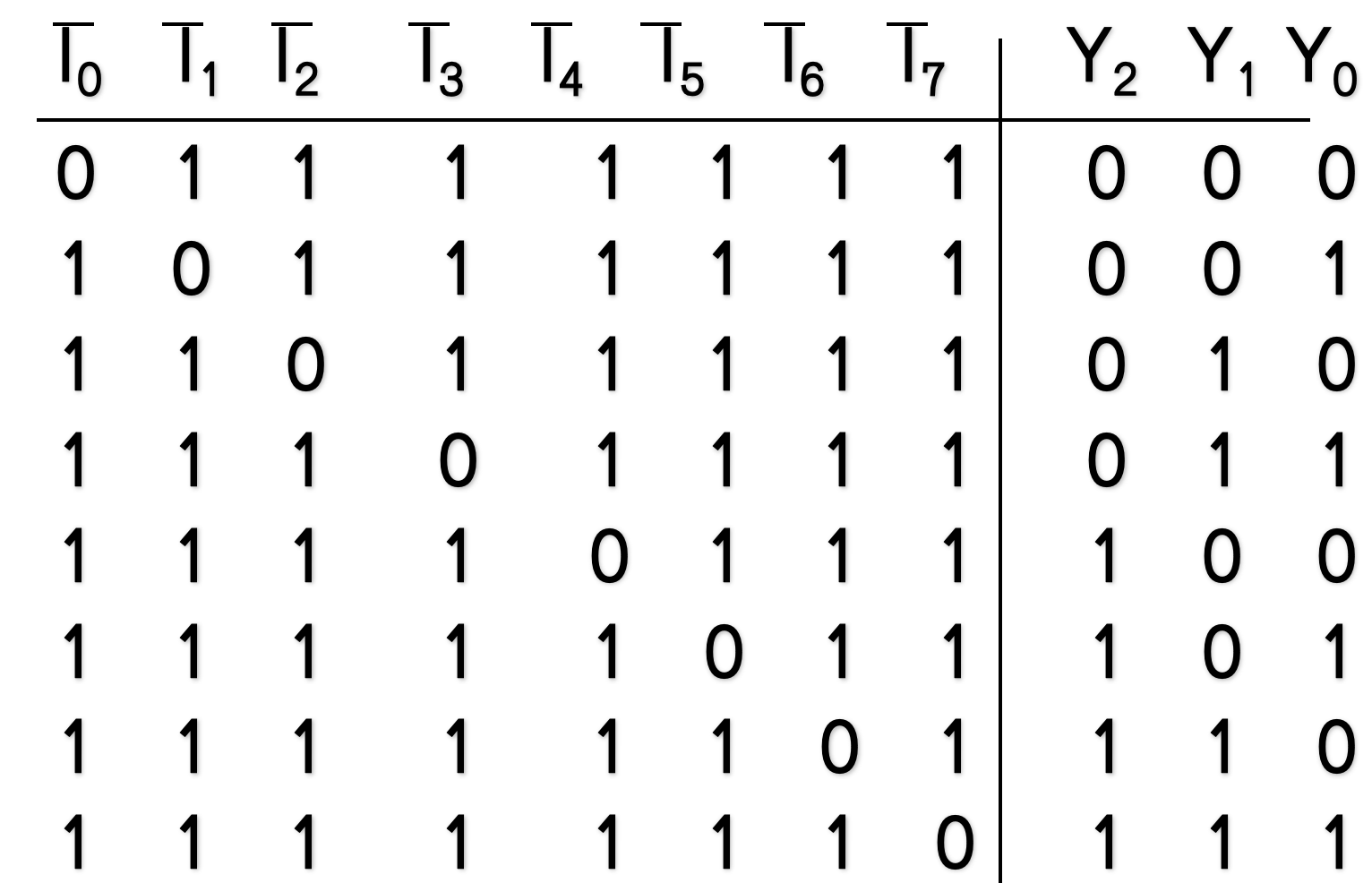


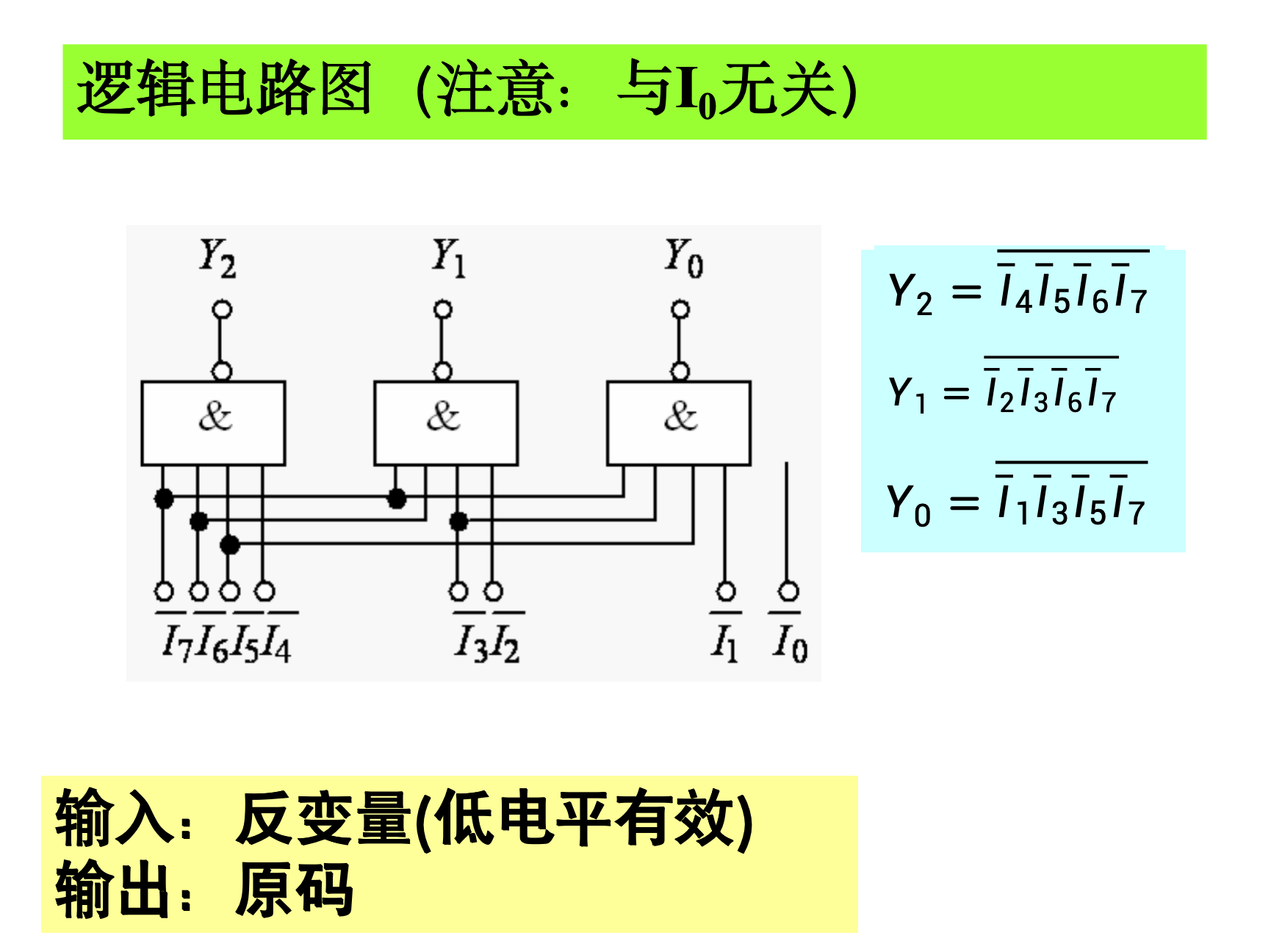
4.3.4 译码器
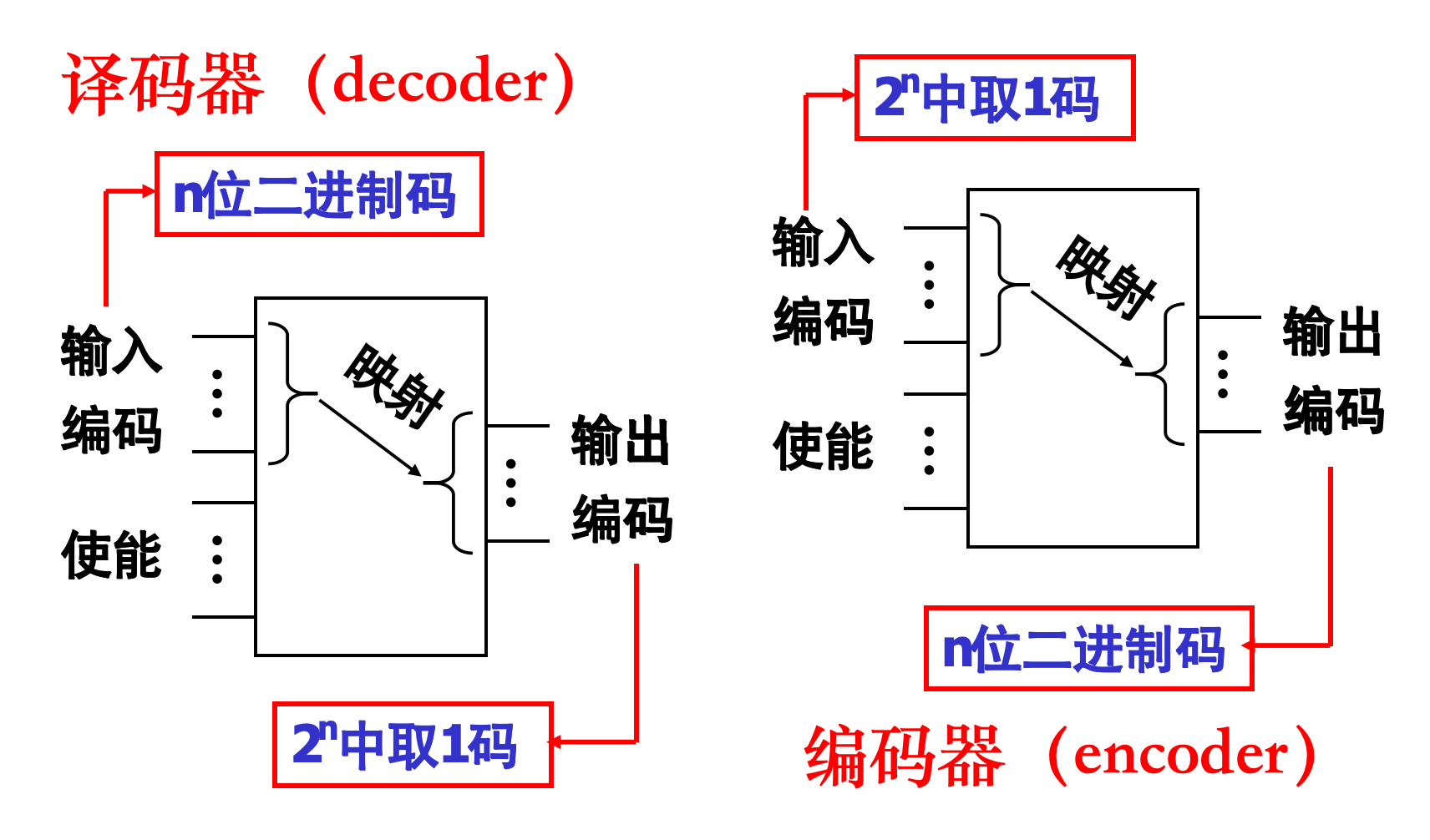
- 译码是编码的逆过程,其功能是将具有特定含义的不同二进制代码"翻译"出来。
4.3.4.1 二进制译码器
-
二进制译码器属于完全译码器
- 完全译码器:设译码器有n个输入和m个输出,则 m = 2 n m=2^n m=2n
- 不满足该条件的称为部分译码器。
-
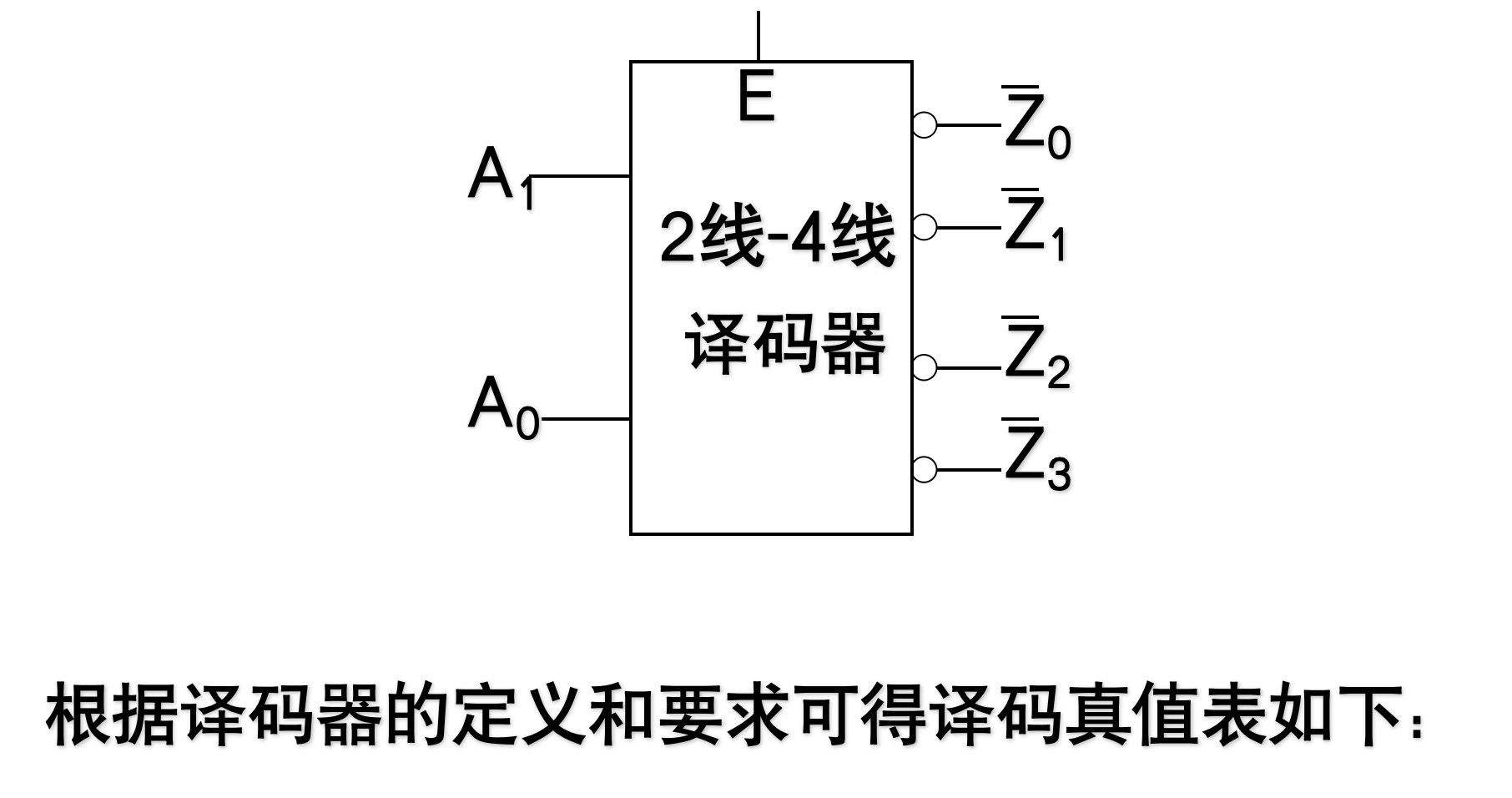
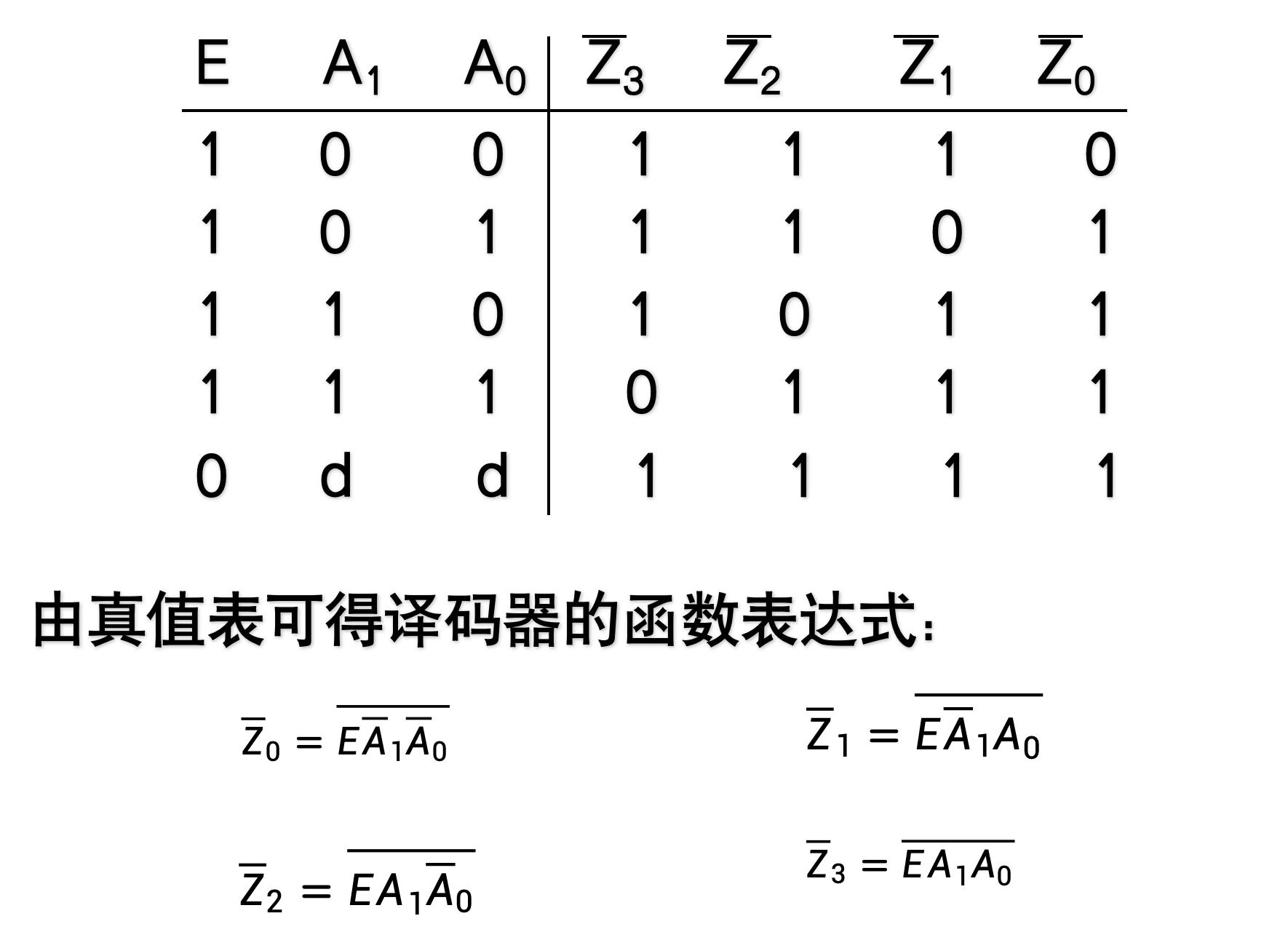
示例:二线-四线译码器
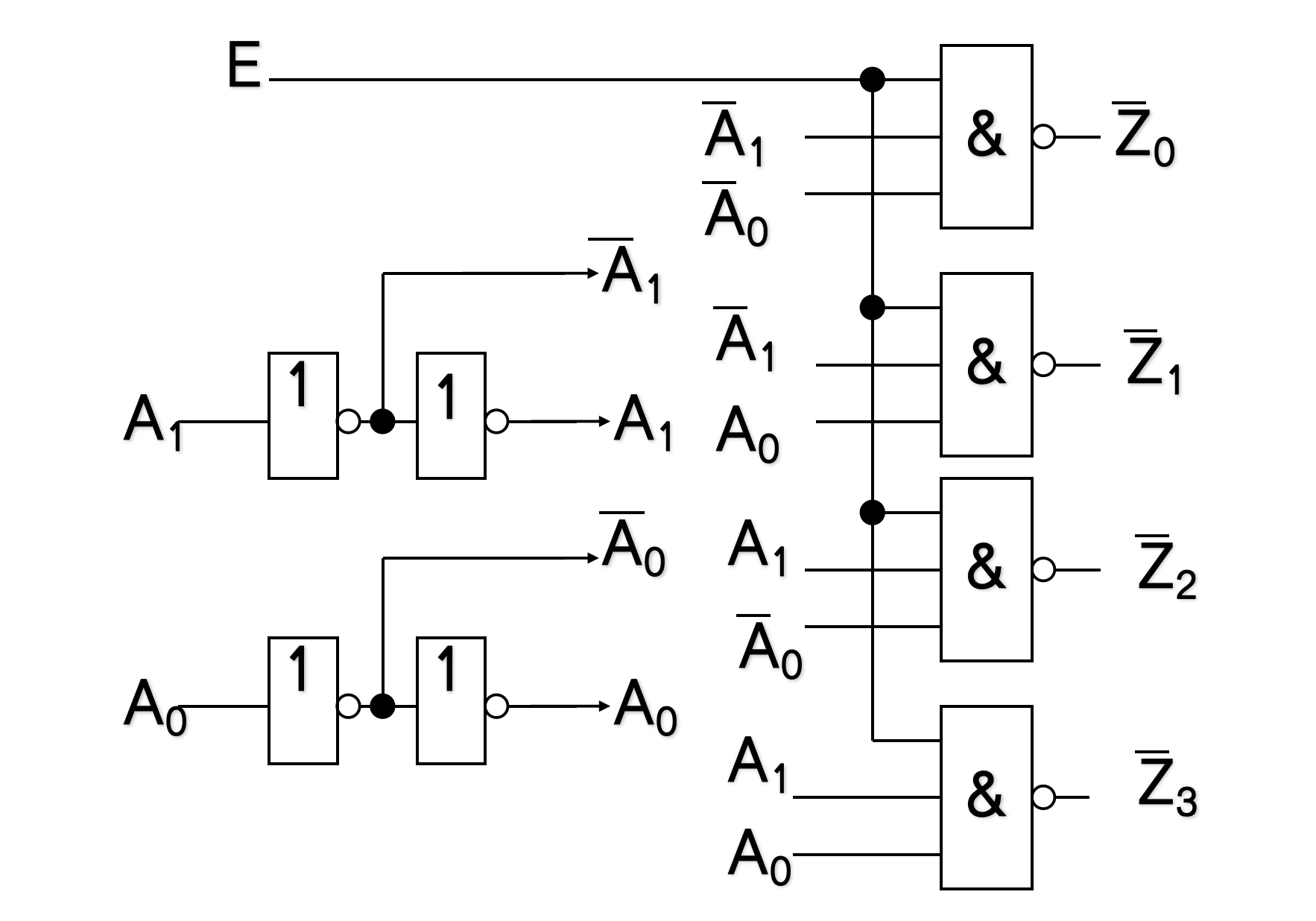
- 完全译码器:设译码器有n个输入和m个输出,则 m = 2 n m=2^n m=2n
4.3.4.2 使能端的作用
- 控制译码器的状态
-
当E=1时,译码器处于工作状态
-
当E=0时,译码器处于非工作状态
-
用于译码器的扩展
-
例:用两片2线-4线译码器扩展成3线-8线译码器。
-
3线-8线译码器的输入为A2、A1、A0,由A2控制两个2线-4线译码器的使能端E。
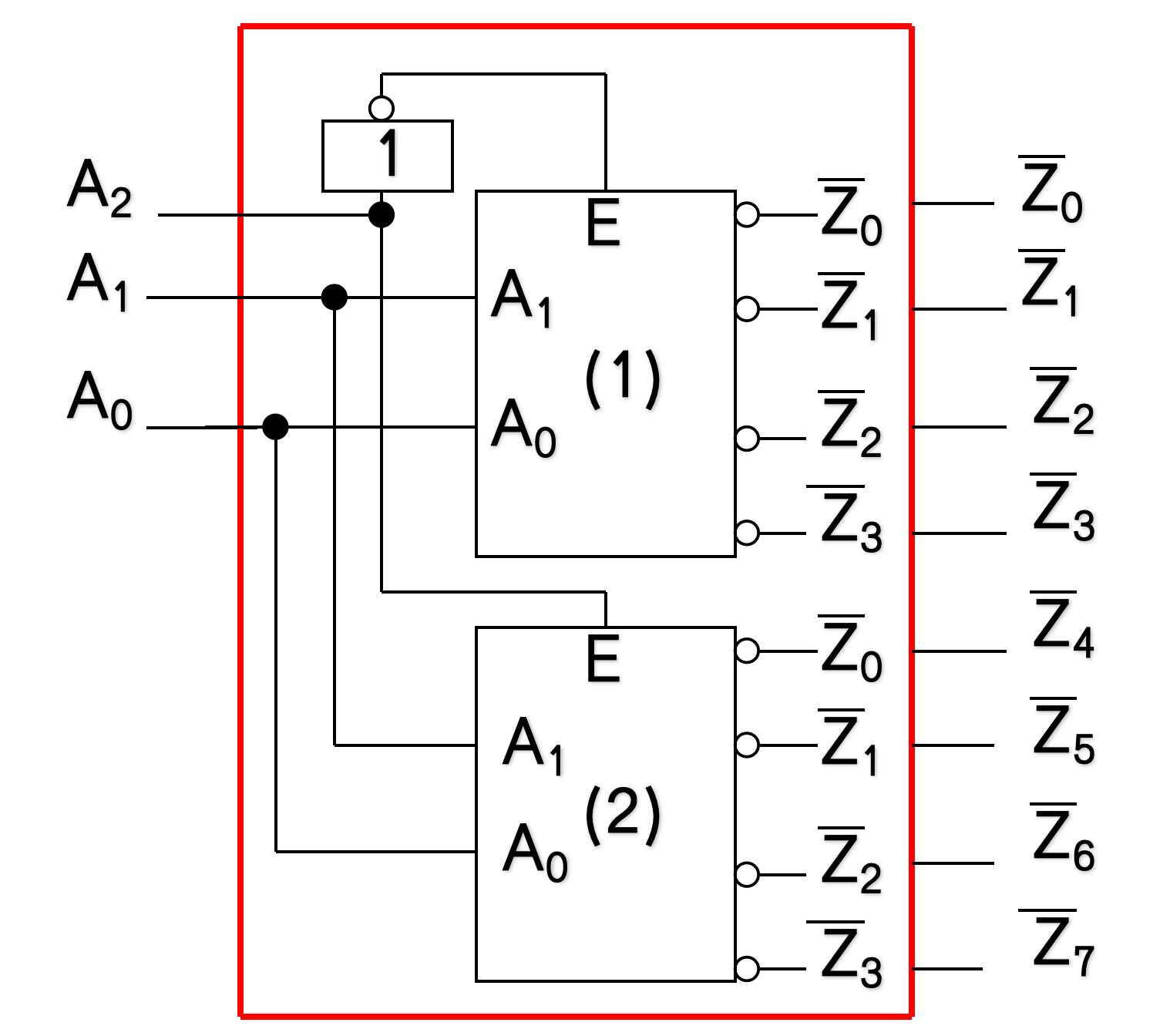


-
设计顶层文件
verilogmodule DEC3_8a_top( input wire[2:0] sw, output wire[7:0] ld ); DEC3_8a D1(.a(sw), .z(ld)); endmodule
-
-
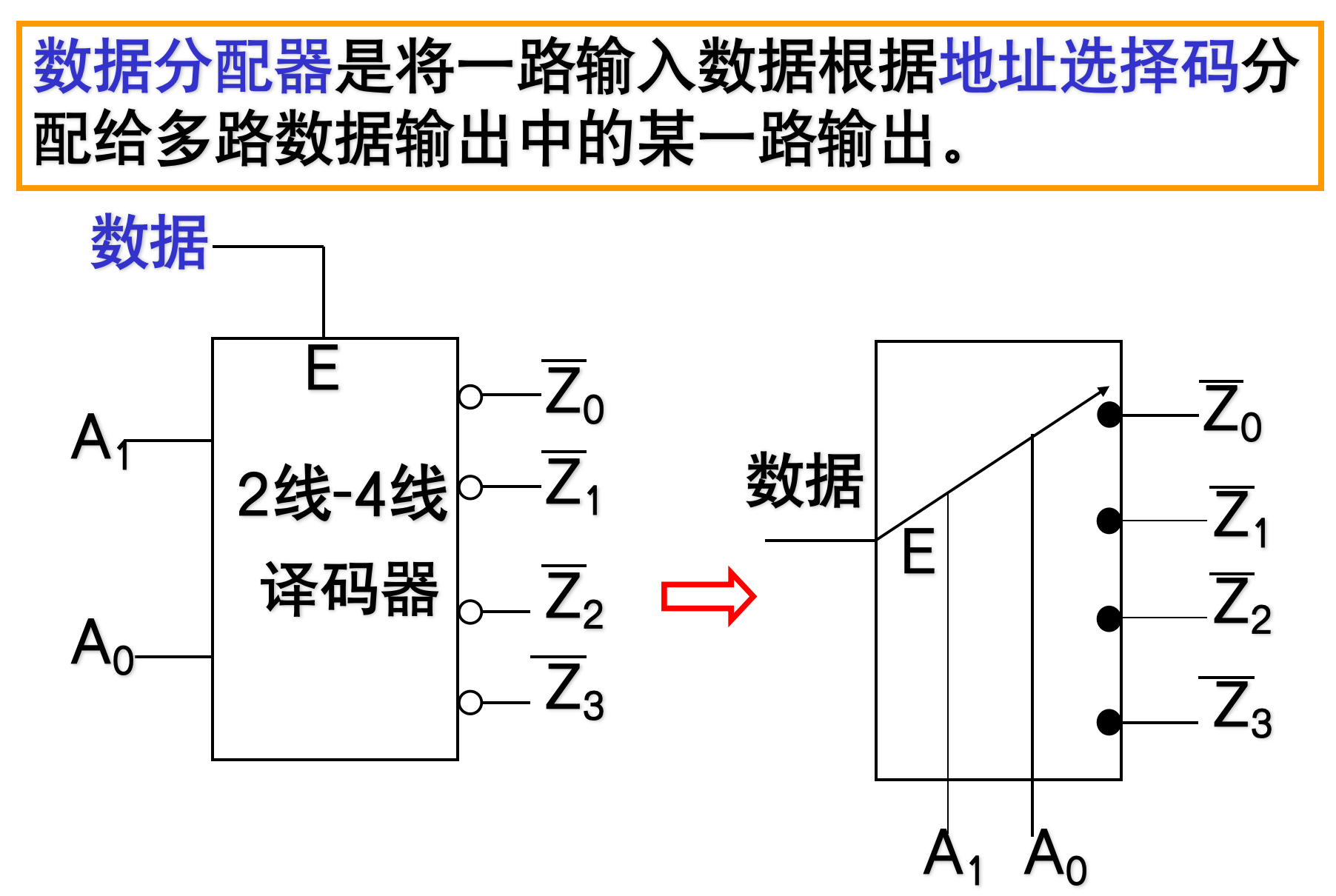
将译码器变为数据分配器

4.3.4.3 二-十进制译码器
-
概述
-
二-十进制译码器的功能是将8421BCD码翻译成十个不同点位的指定电平。
- 如果指定为低电平有效,那么使能端E为"1"时,译码器处于工作状态;
- 使能端E为"0"时,译码器被封锁,输出全为"1" 。


-
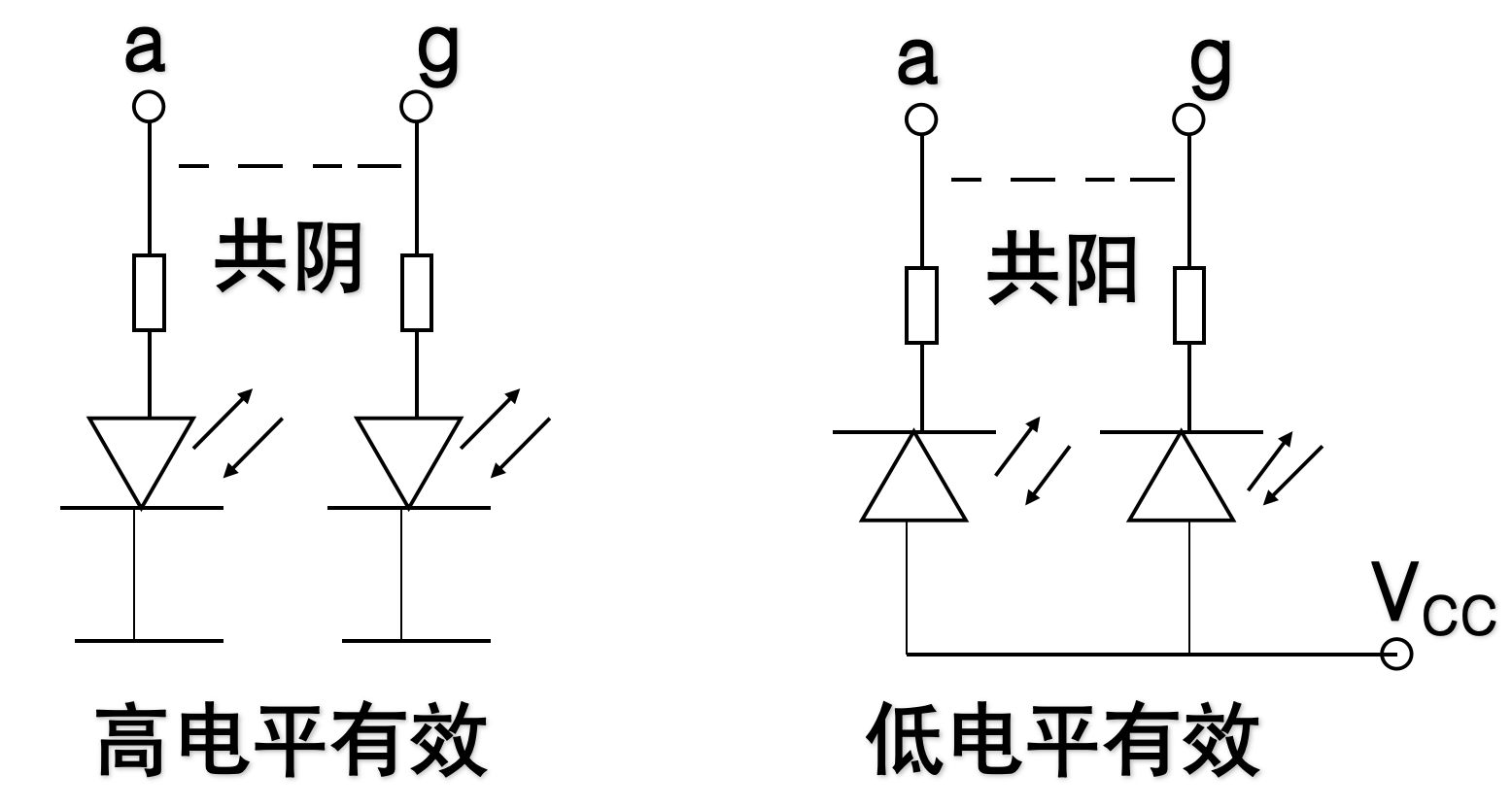
4.3.4.4 数字显示译码器
-
要求用与非门设计一个8421BCD码~七段数字显示译码器。
-
PPT32-42有示例和实验课的内容类似
4.3.4.5 译码器的应用
重点!!!
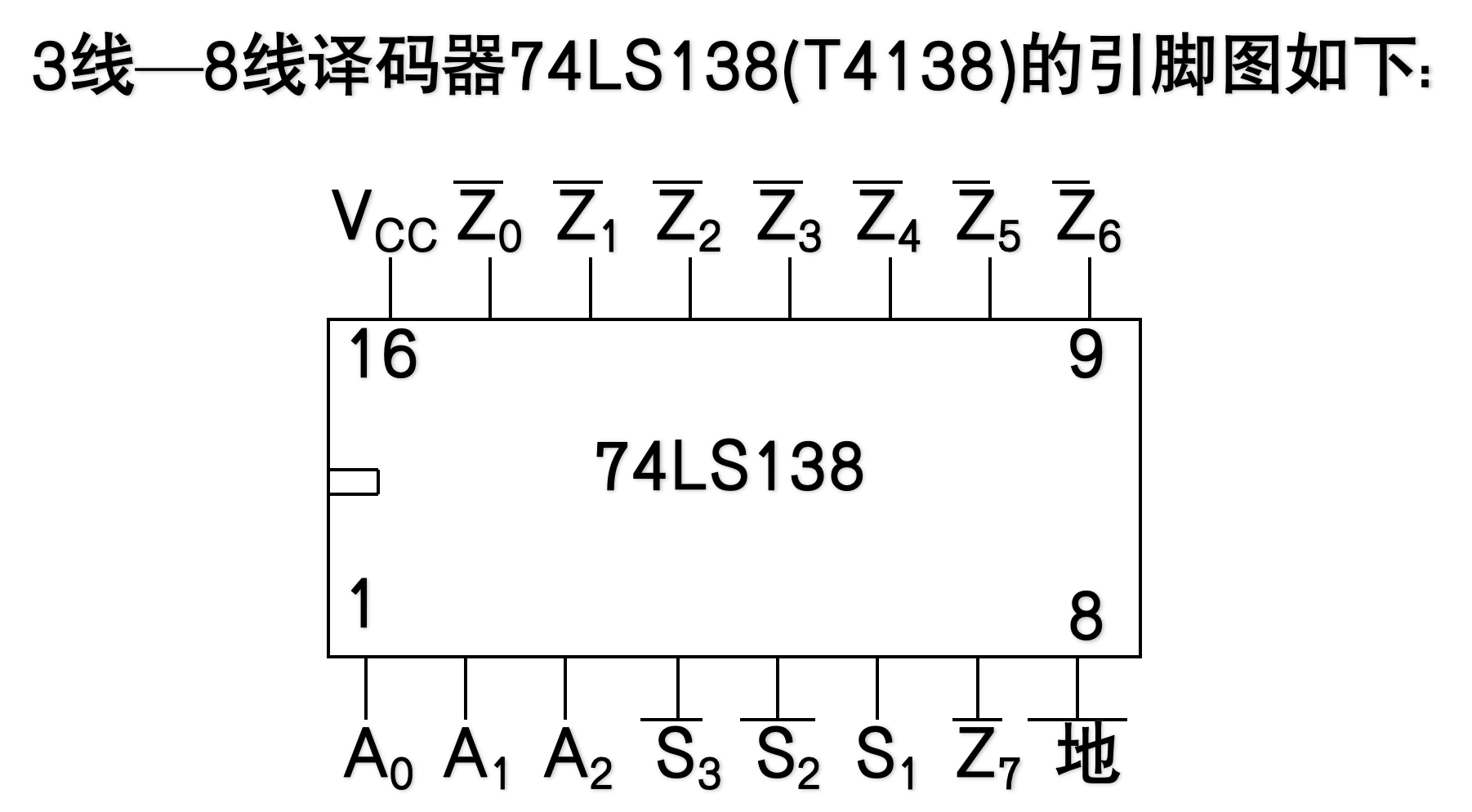
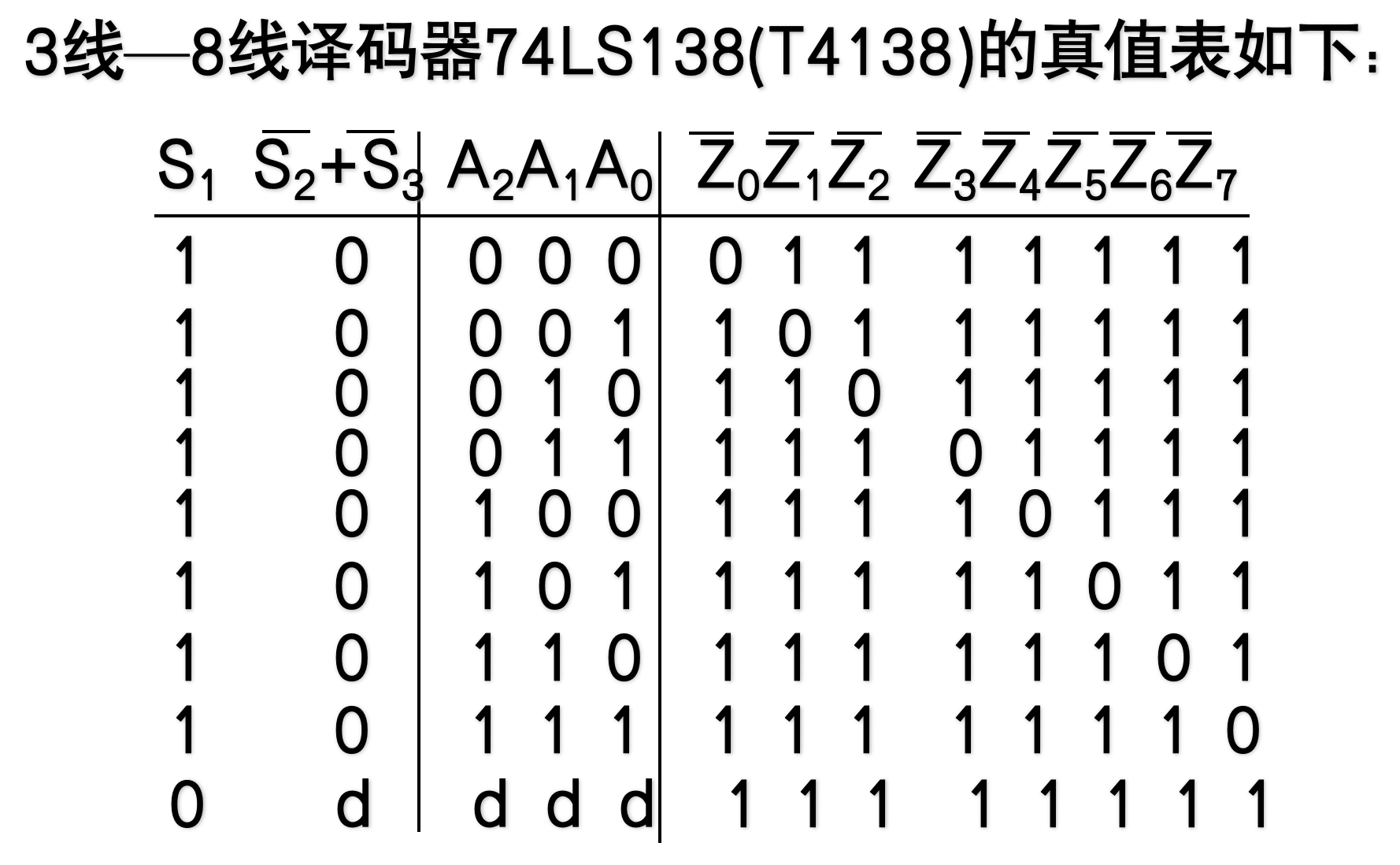

-
示例


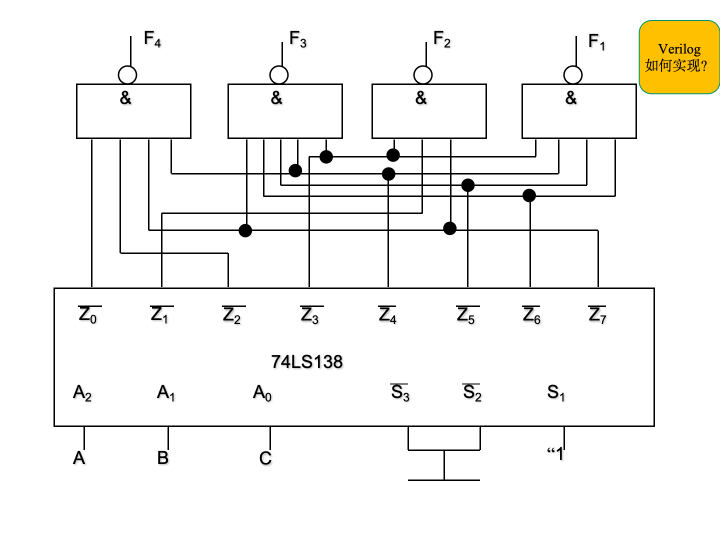
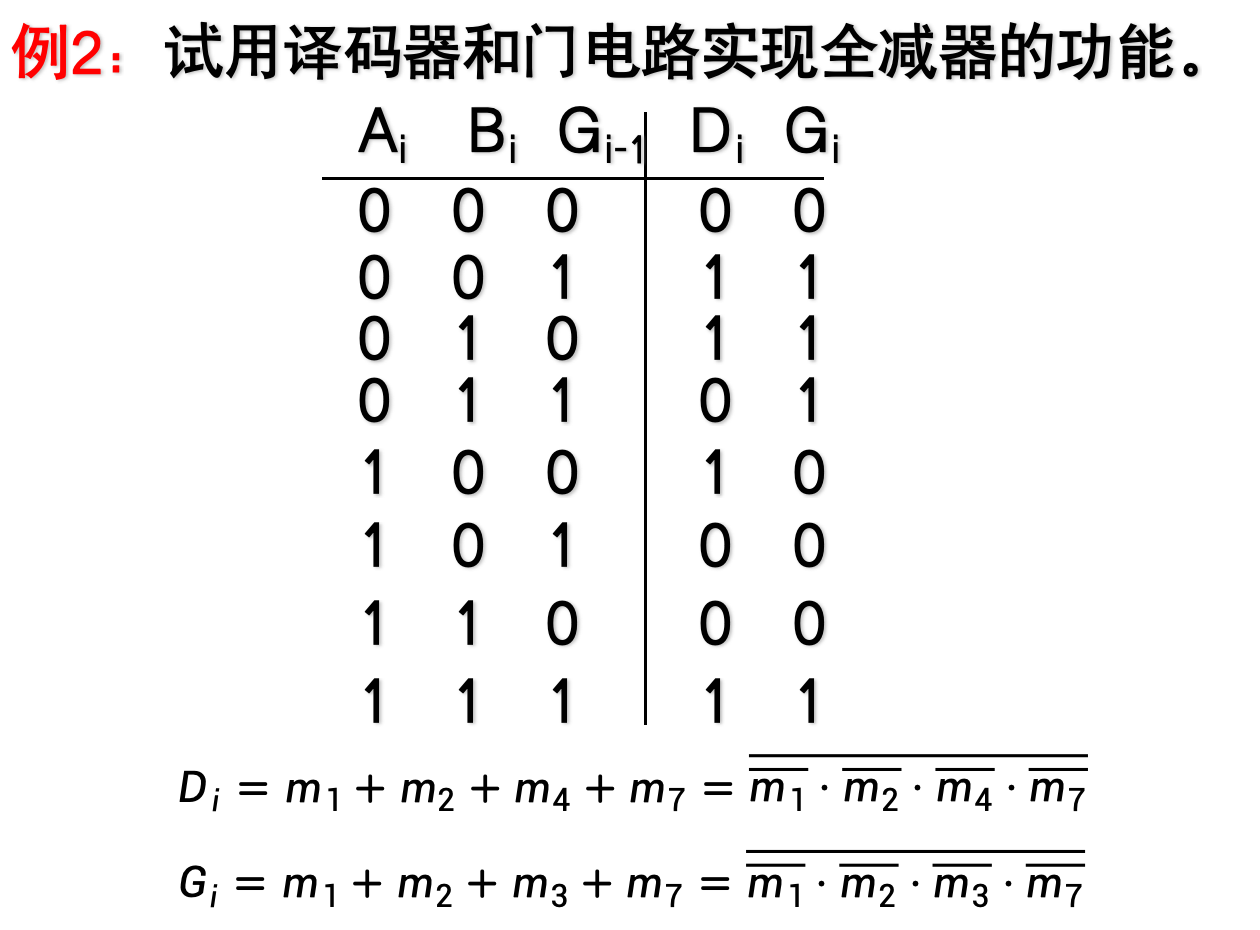
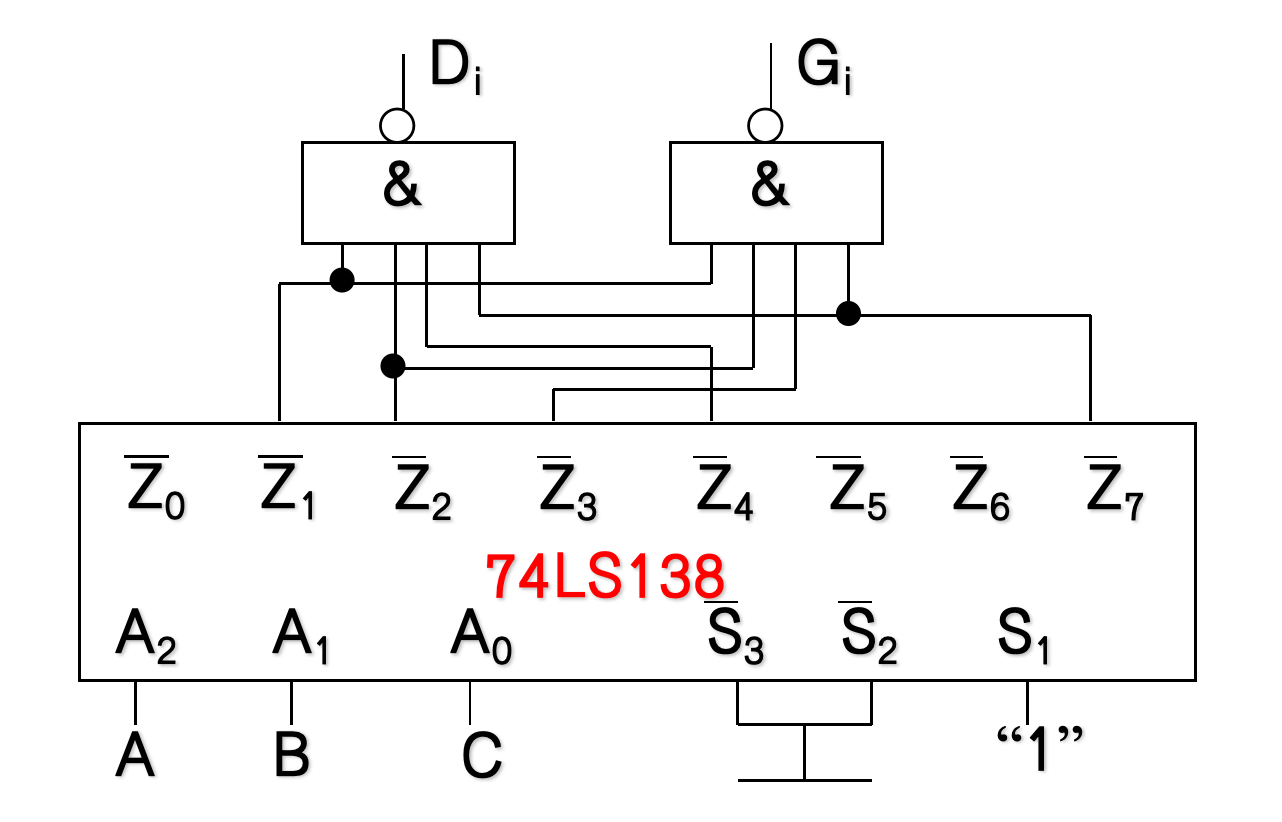
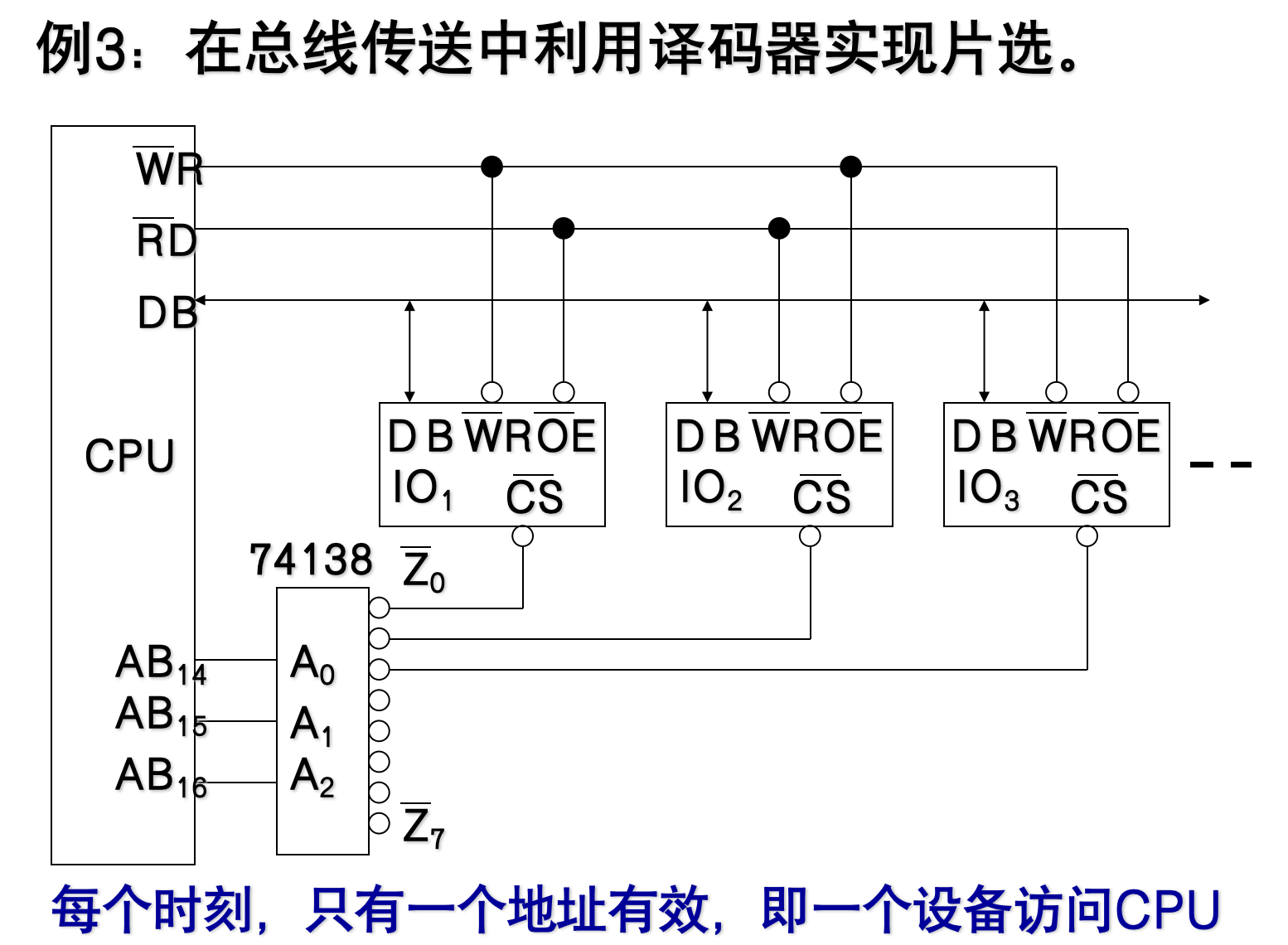
4.3.5 代码转换电路
4.3.5.1 8421BCD码转换为余三码
-
余三码 = 8421BCD码 + 3
- 也就是说,对于同一个十进制数字,余三码比对应的8421BCD码大3。
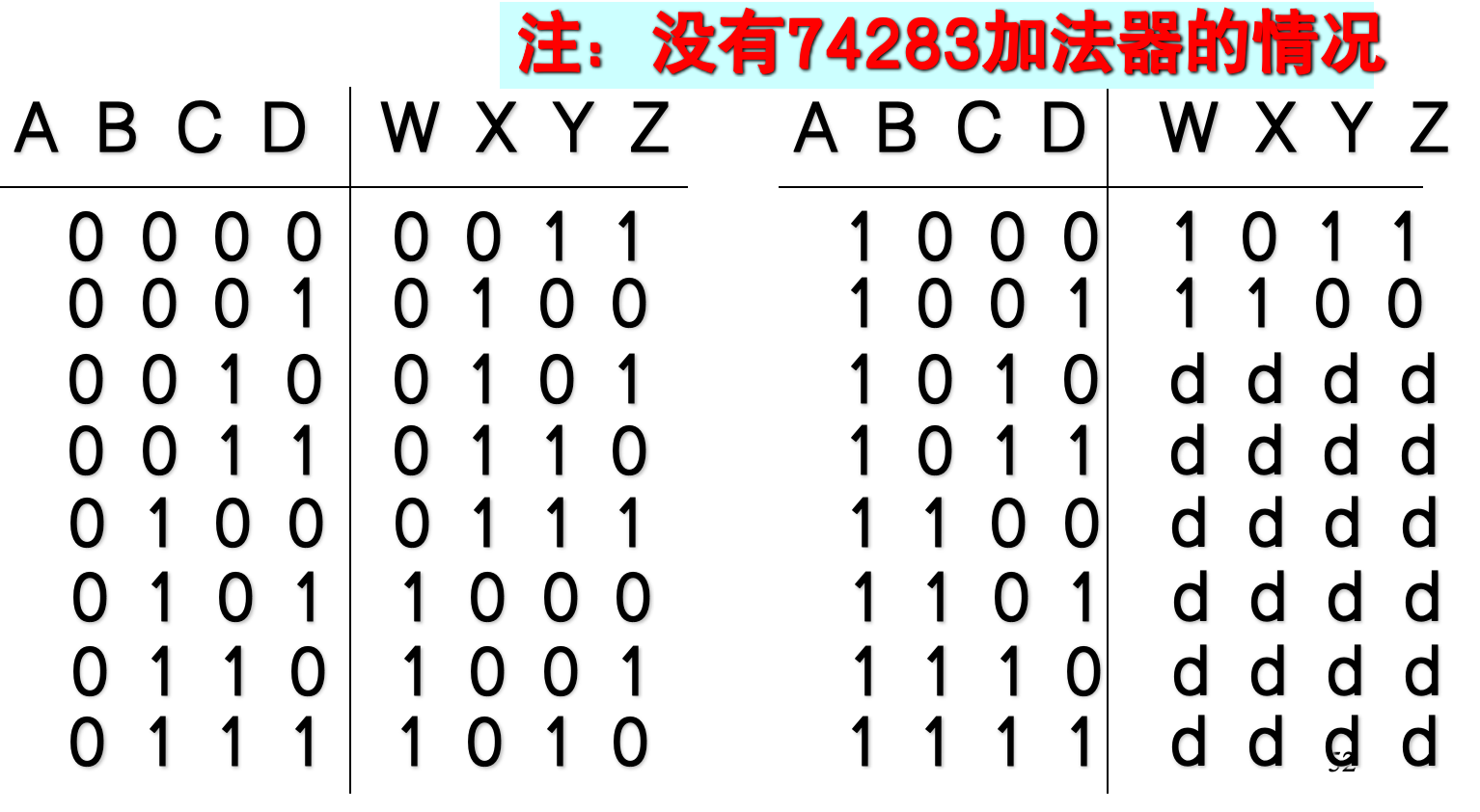
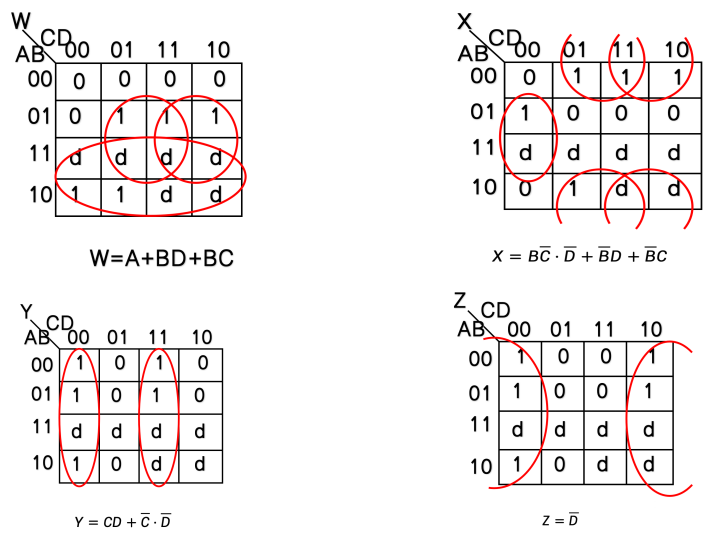
-
"d"(无关项)到底是什么?
-
在BCD码中,十进制数只有0-9(对应二进制0000到1001)是有效的。
-
二进制1010到1111(十进制10-15)这6个组合是无效的,在BCD系统中永远不会出现。
-
既然这些输入组合在实际电路中根本不会发生,那么它们的输出是0还是1就无关紧要(Don't Care),我们用"d"表示。
-
因此我们可以自由选择将"d"视为"1"或"0",哪个能带来更简化的结果就选哪个!
-
4.3.5.2 四位二进制代码转换为格雷码
- 格雷码(Gray Code) ,也叫循环码或反射二进制码,是一种非常重要的二进制编码方式。
- 最大特点:相邻两个数字的二进制表示只有一位不同

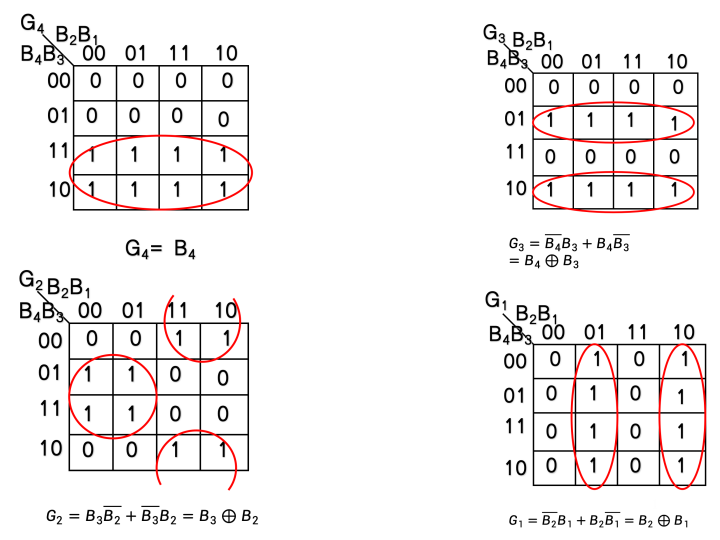
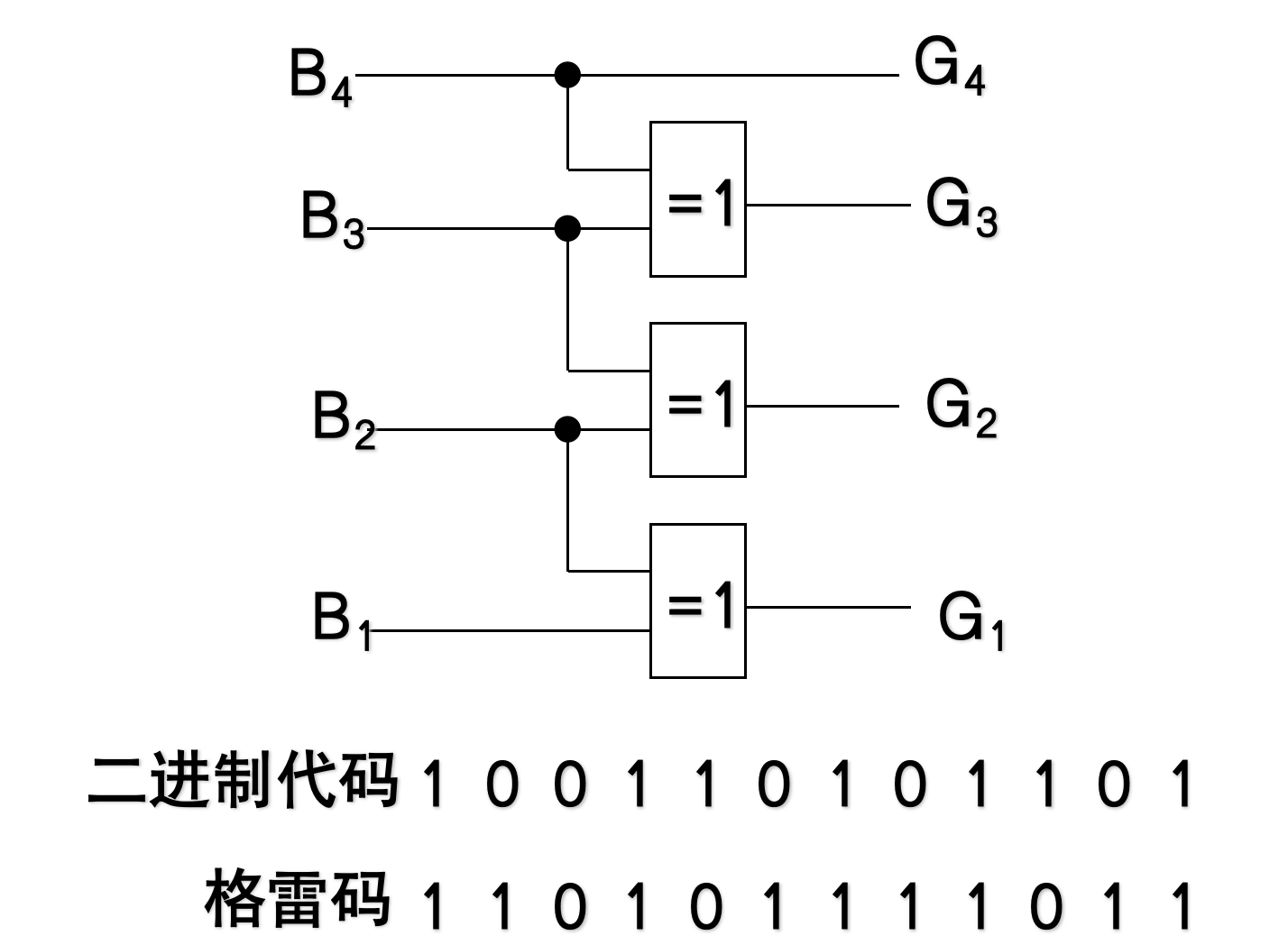
4.3.6 数字选择器
- 数据选择器是根据地址选择码从多路输入数据中选择一路数据输出,也称复用器。
- 本小节的代码都建议自己重新写一遍
4.3.6.1 2选1数据选择器
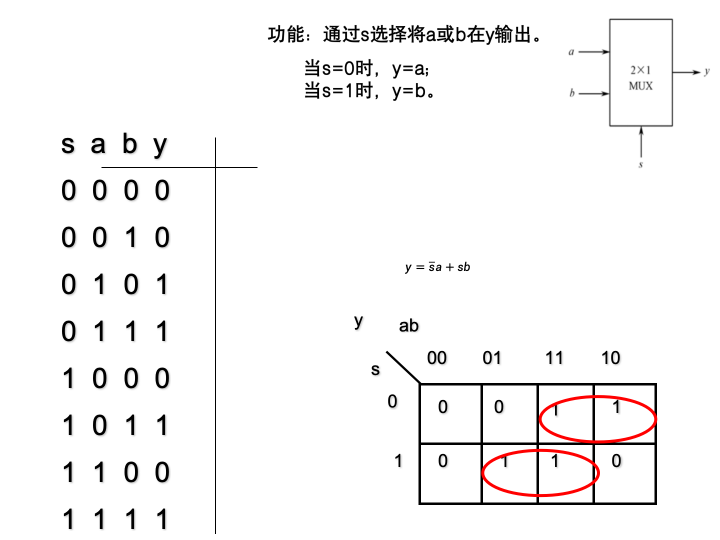
-
门级Verilog描述
verilogmodule mux21a(a, b, s, y); input a, b, s; output y; wire ns, c, d; not U1(ns,s); and U2(c, ns, a); and U3(d, s, b); or U4(y, c, d); endmodule -
数据流级Verilog描述
verilogmodule mux21a(a,b,s,y); input a, b, s; output y; assign y=(~s&a)|(s&b); endmodule -
行为级Verilog描述
-
if语句
verilogmodule mux21a(a,b,s,y); input wire a; input wire b; input wire s; output reg y; always @(a,b,s) if (s==0) y = a; else y = b; endmodule -
case语句
verilogalways @(a,b,s) case(s) 0: y=a; 1: y=b; endcase -
用?语句
verilogassign y = s ? b:a;
-
-
设计顶层文件
verilogmodule mux21_top( input wire [1:0] sw, input wire btn, output wire ld ); mux21c M1(.a(sw[0]), .b(sw[1]), .s(btn), .y(ld) ); endmodule
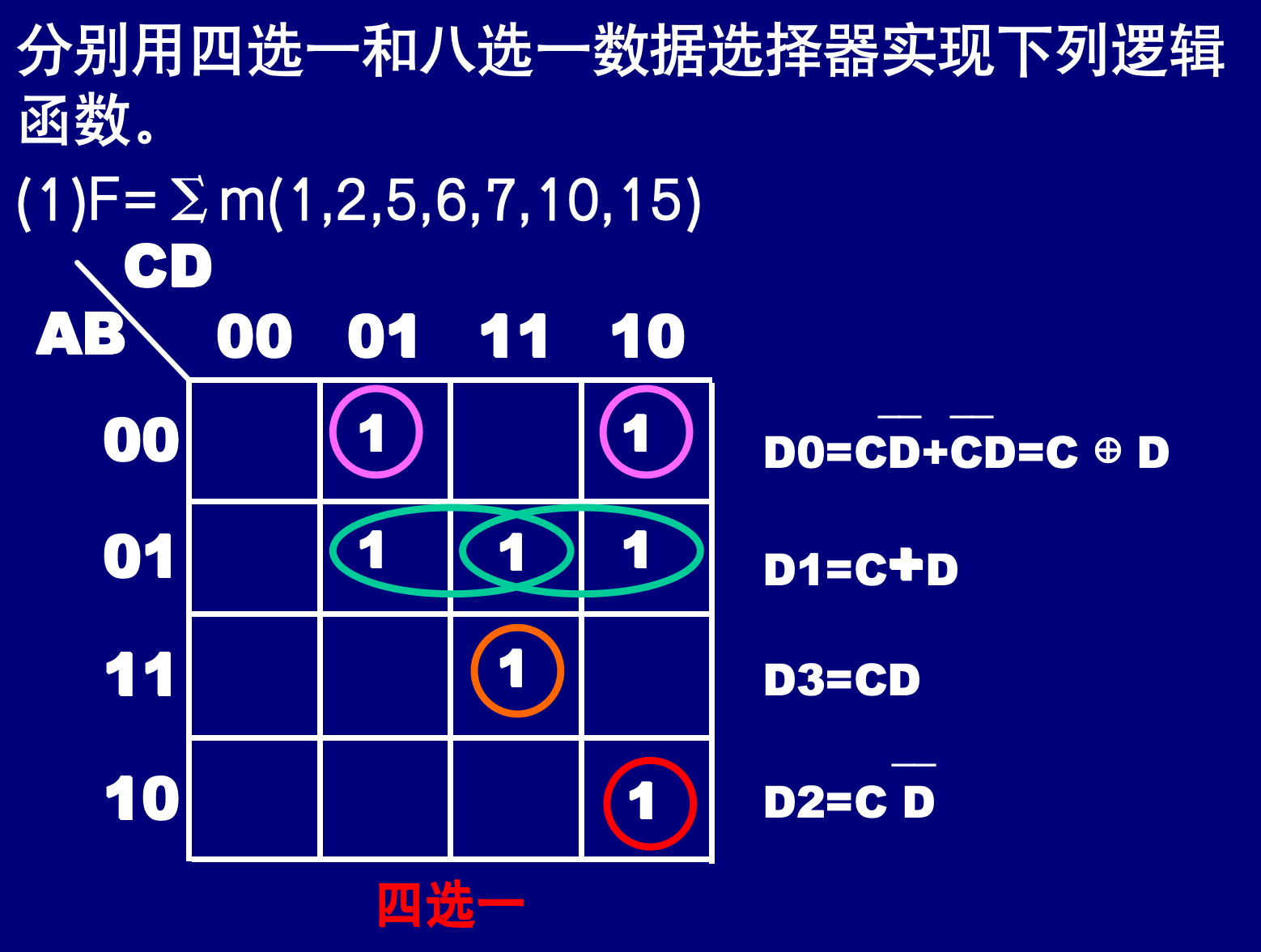
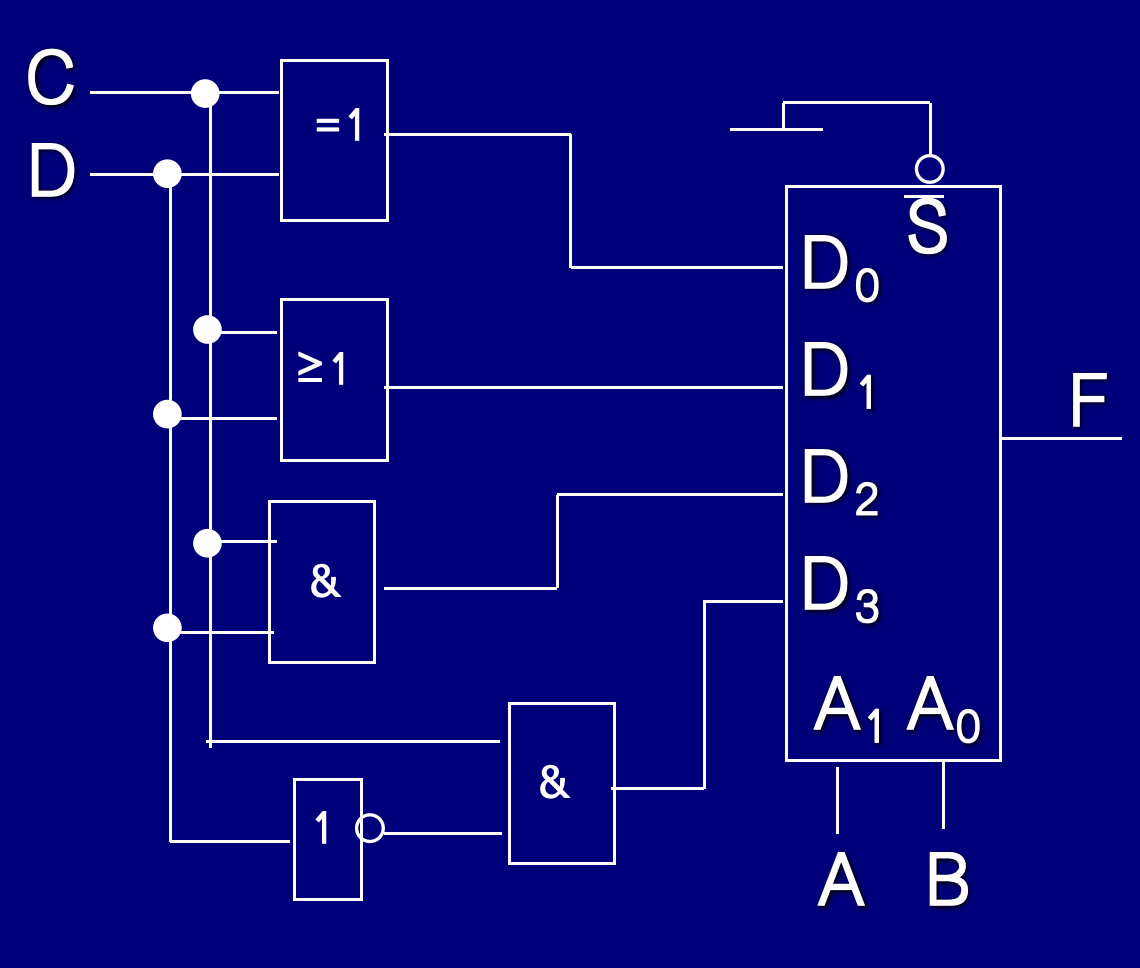
4.3.6.2 4选1数据选择器
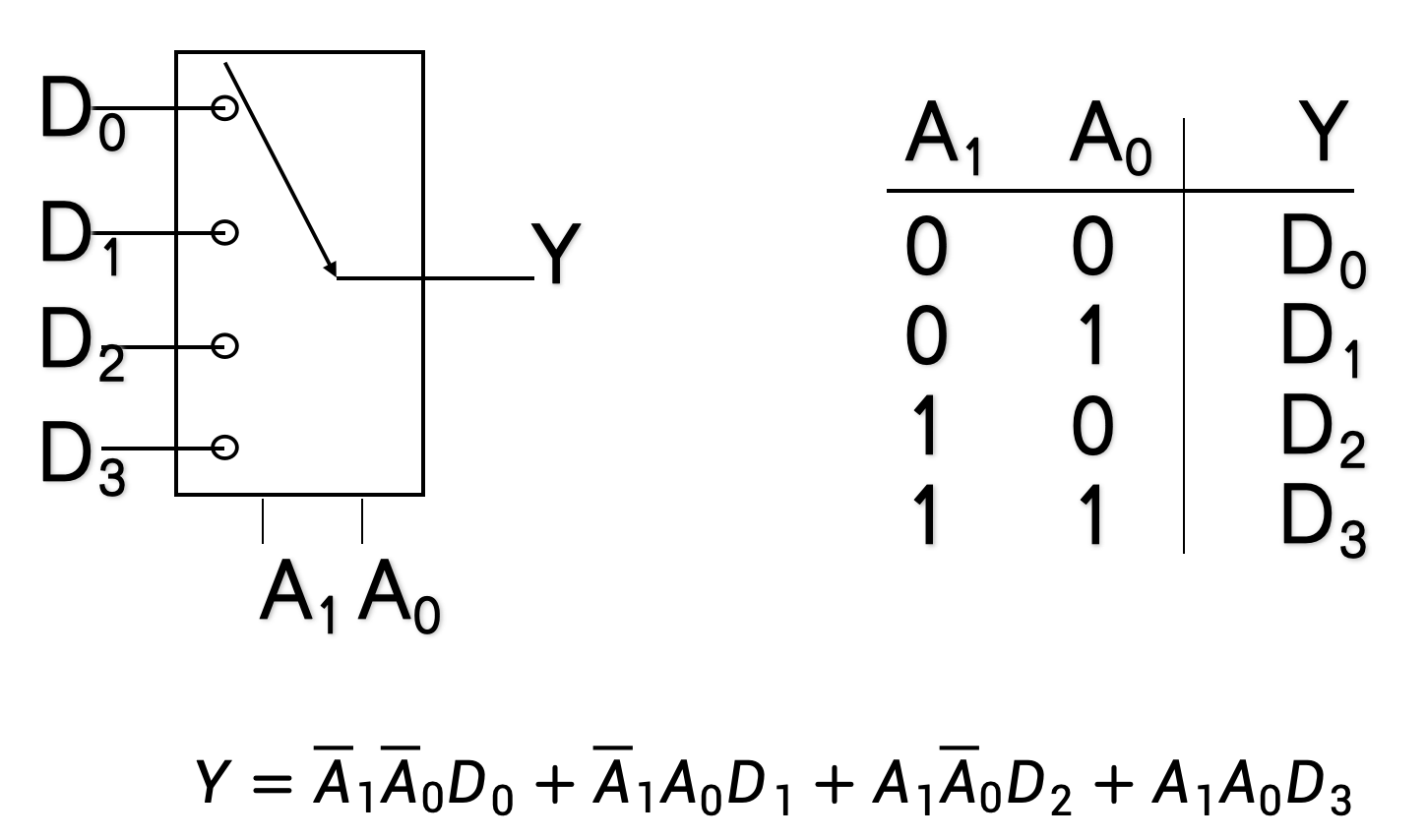
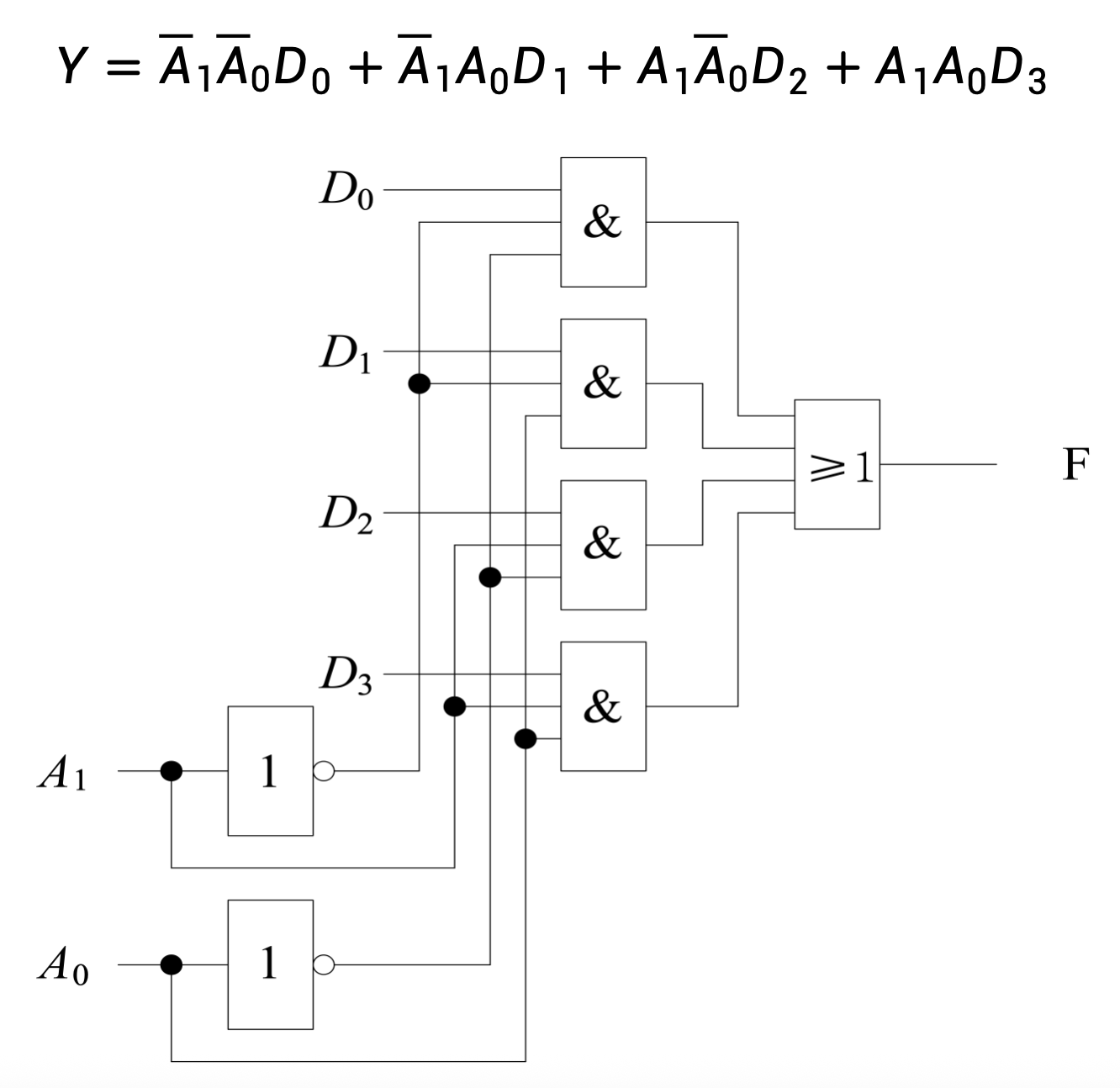
- PPT 11-13页有对应的代码
4.3.6.3 4位2选1多路选择器
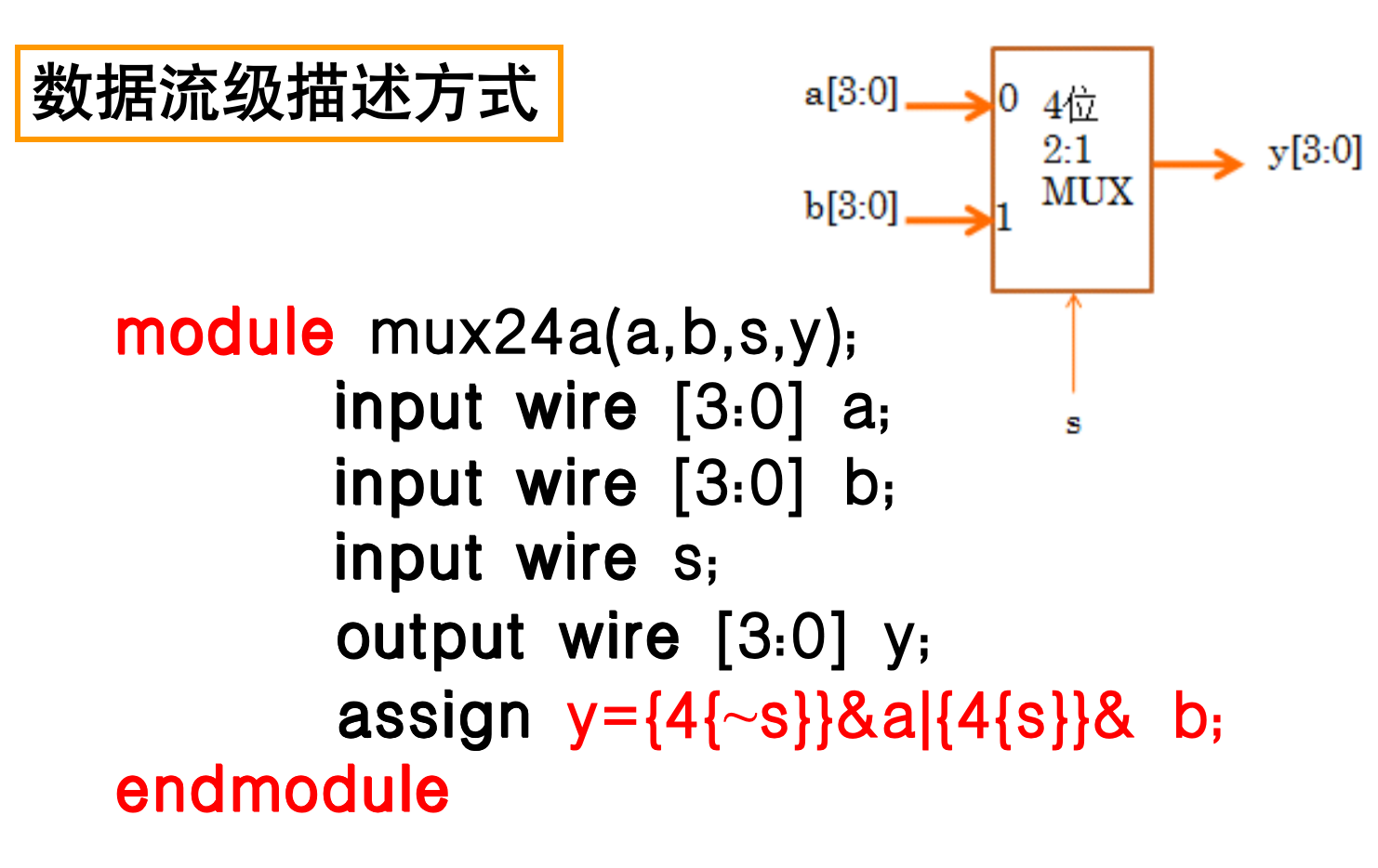
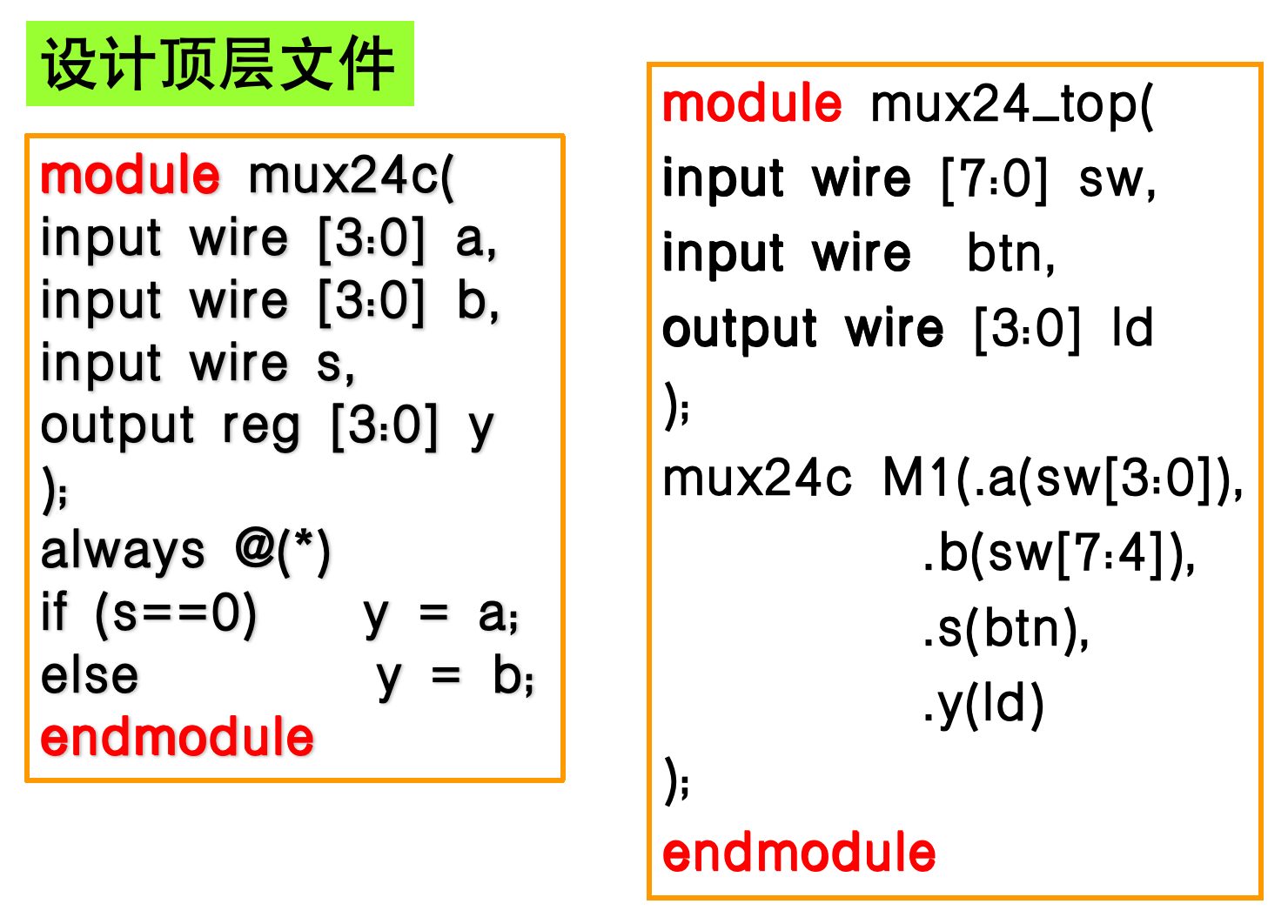
-
在
always过程块内被赋值的信号,必须声明为reg类型。 -
直接被模块实例端口驱动的信号,应声明为
wire类型。
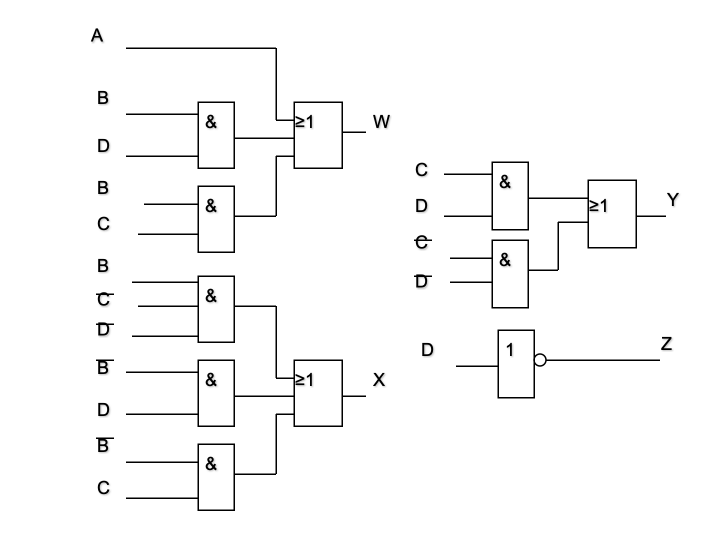
4.3.6.4 数据选择器的应用
-
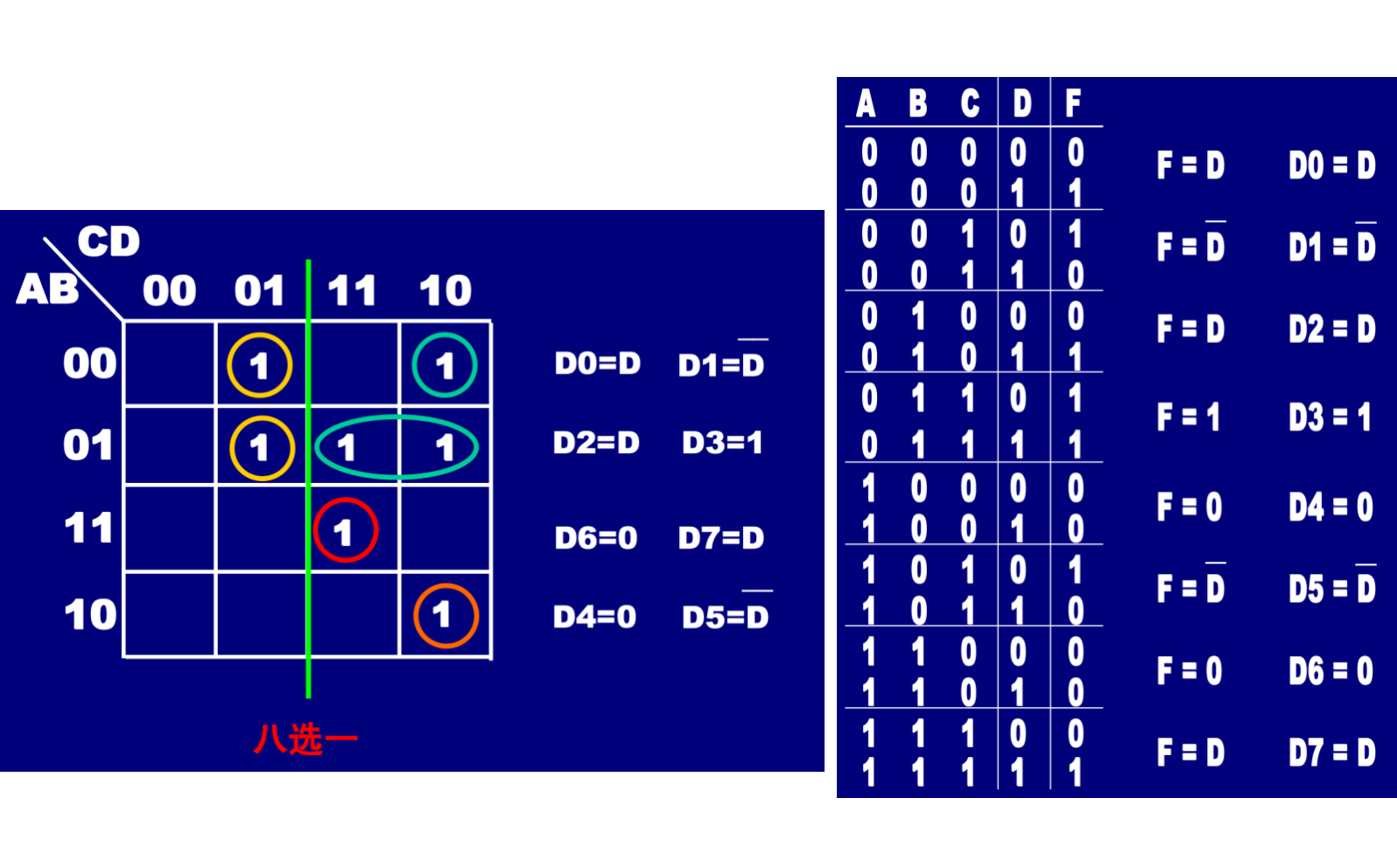
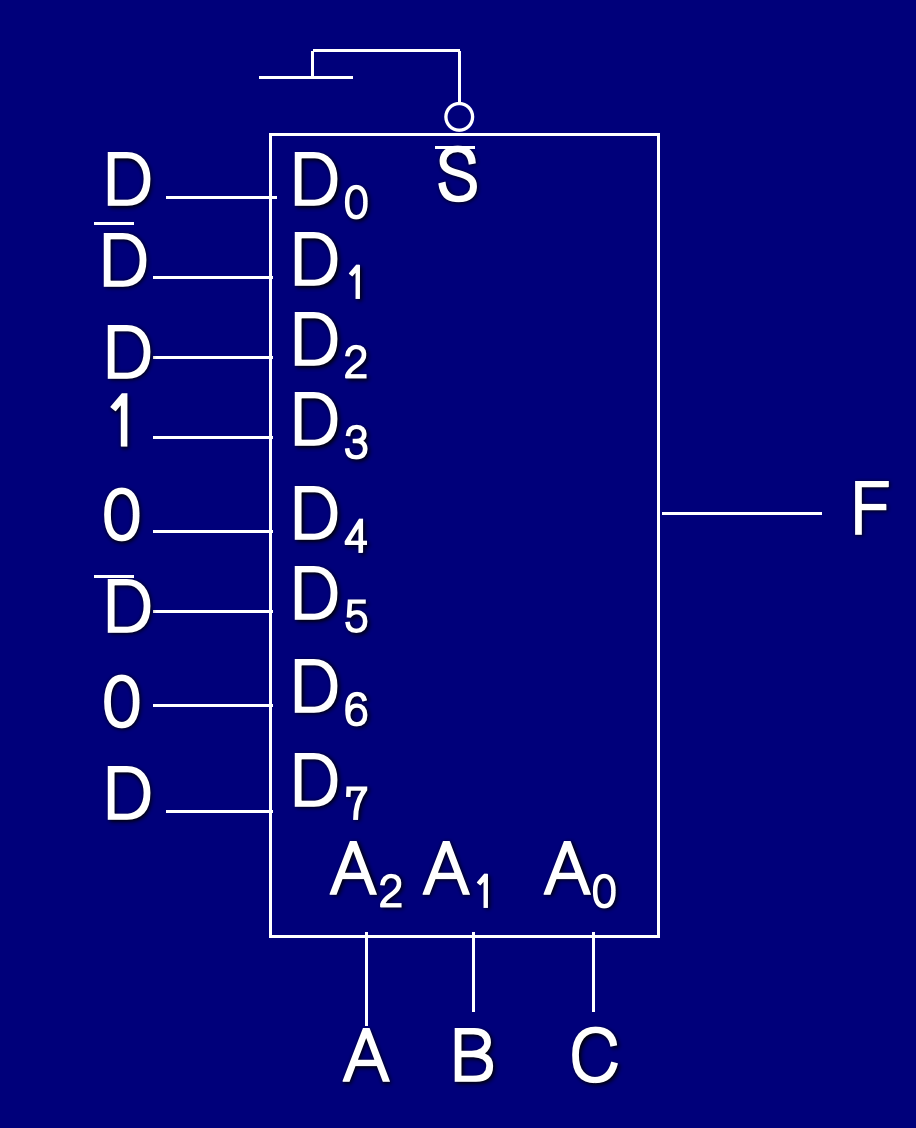
利用 2 n 2^n 2n路数据选择器可以很方便地实现任一个n变量的逻辑函数表达式。
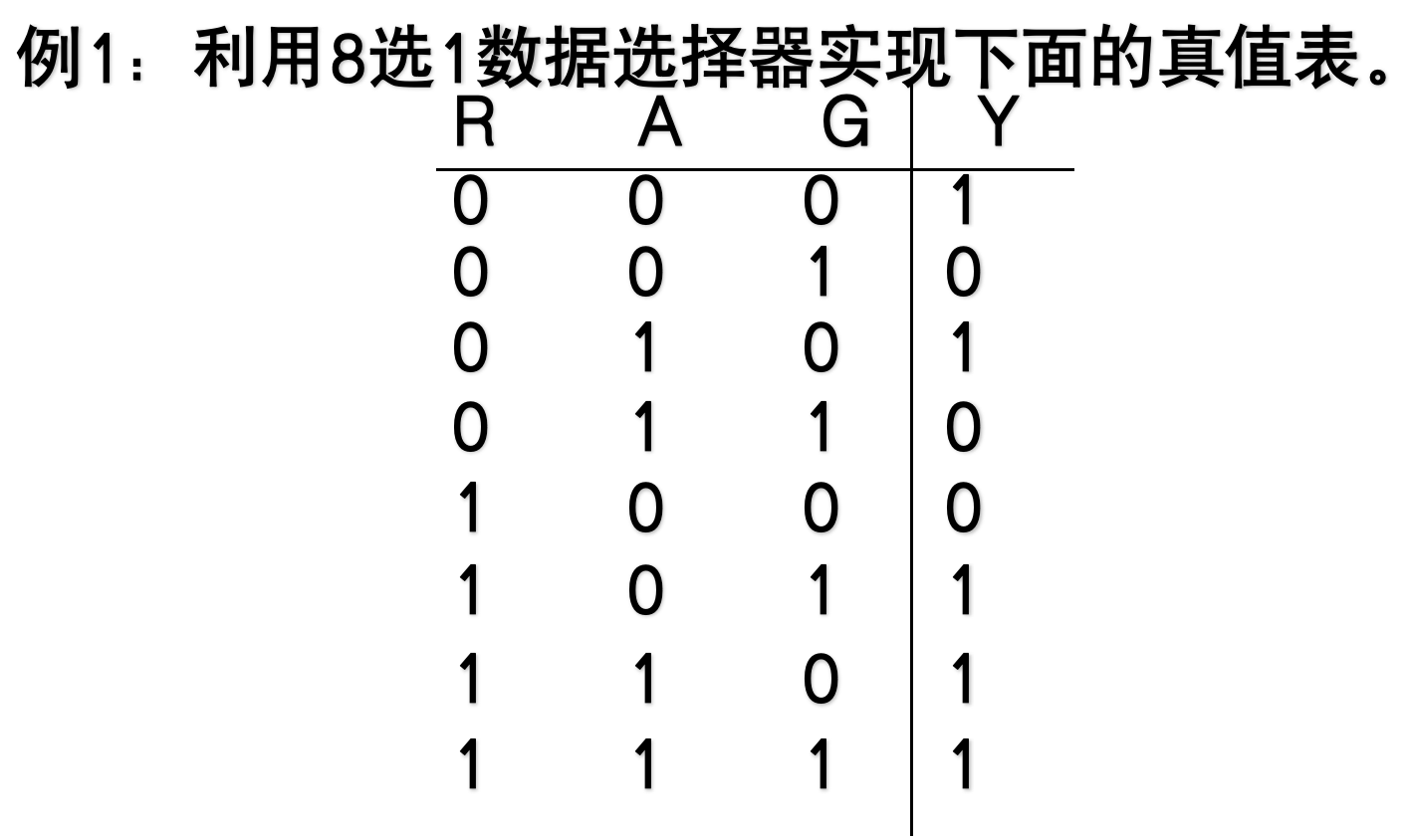
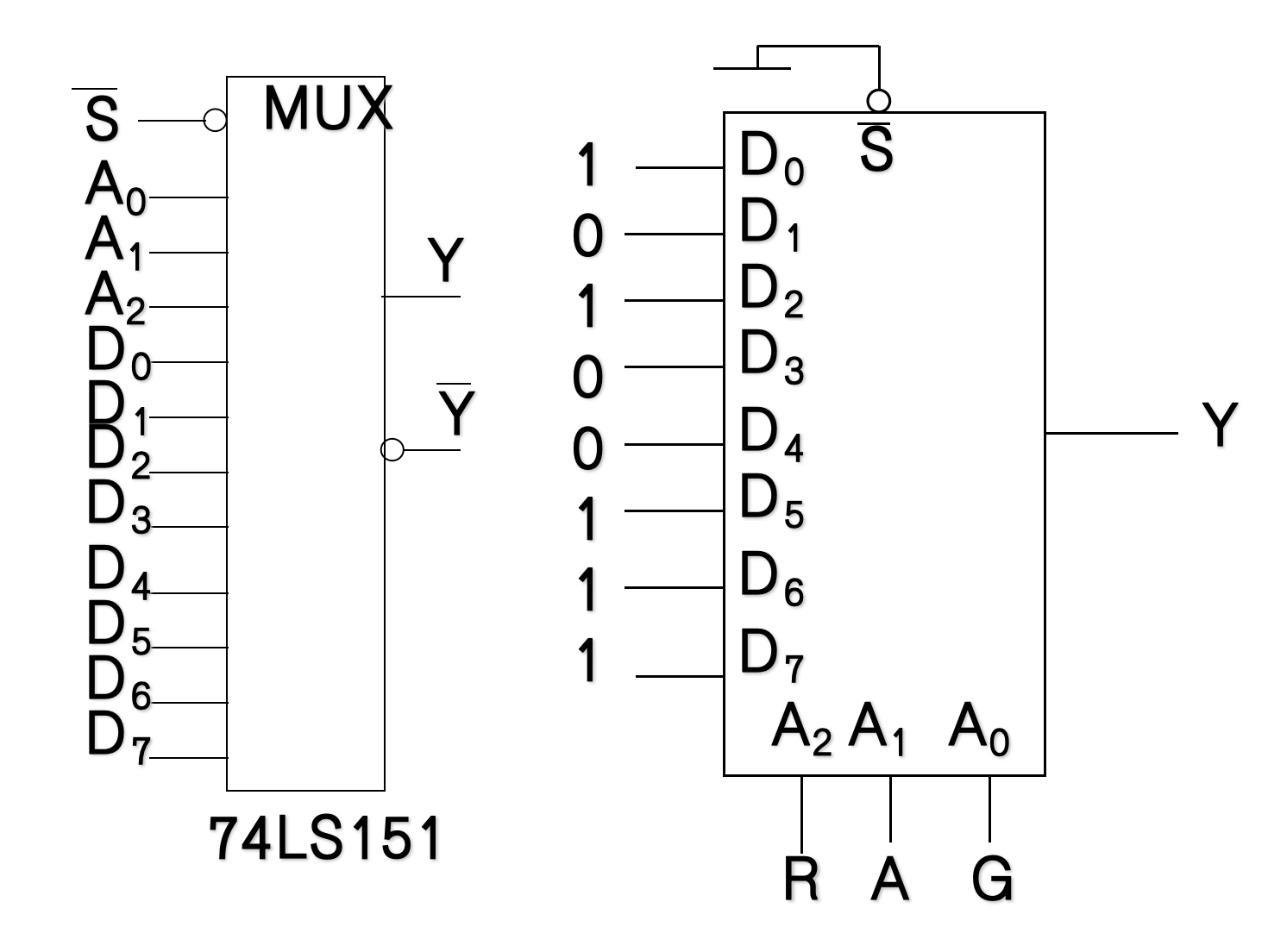
-
其中R、A、G是数据选择信号,D0-D7为对应的数据路线
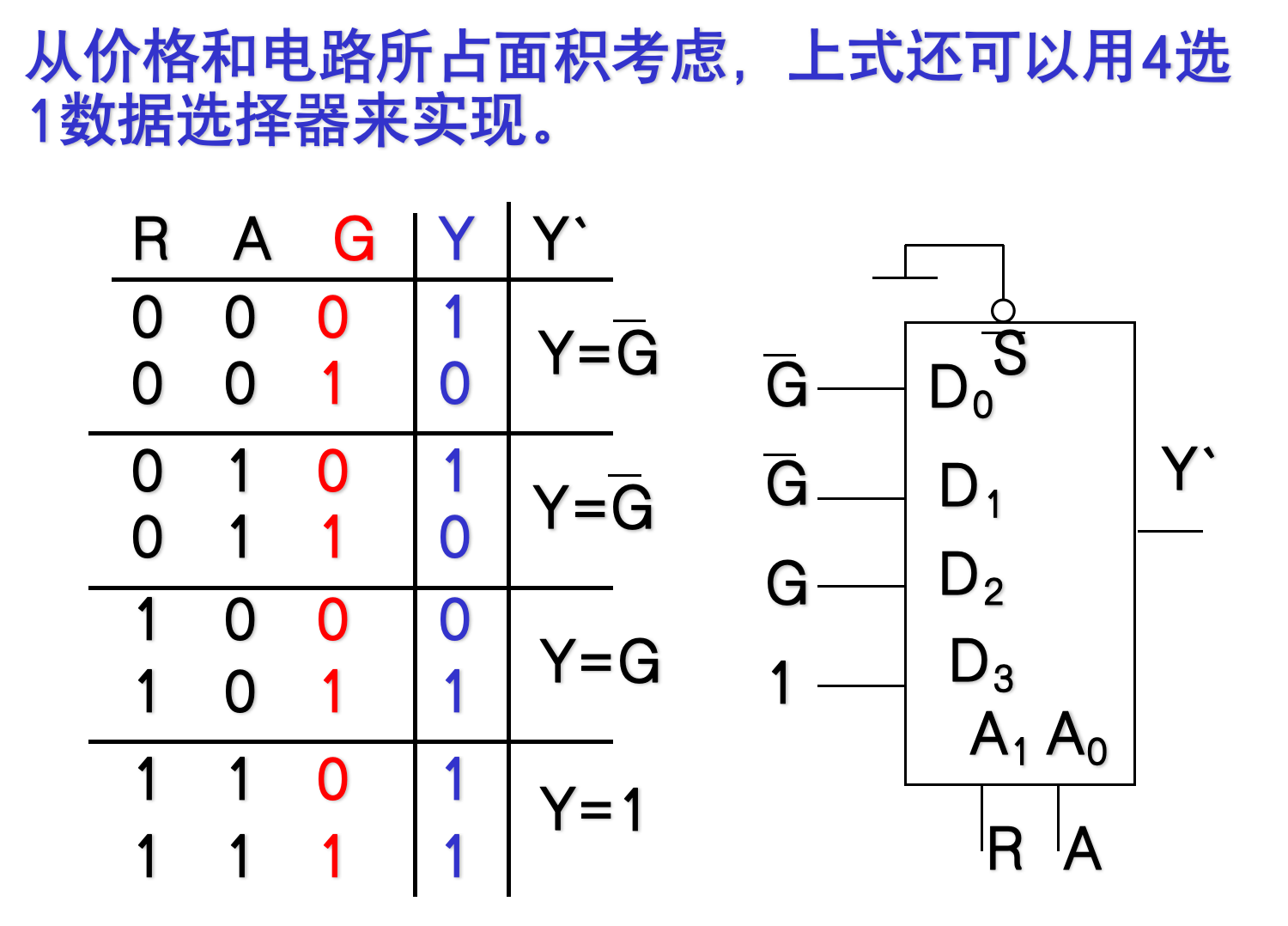
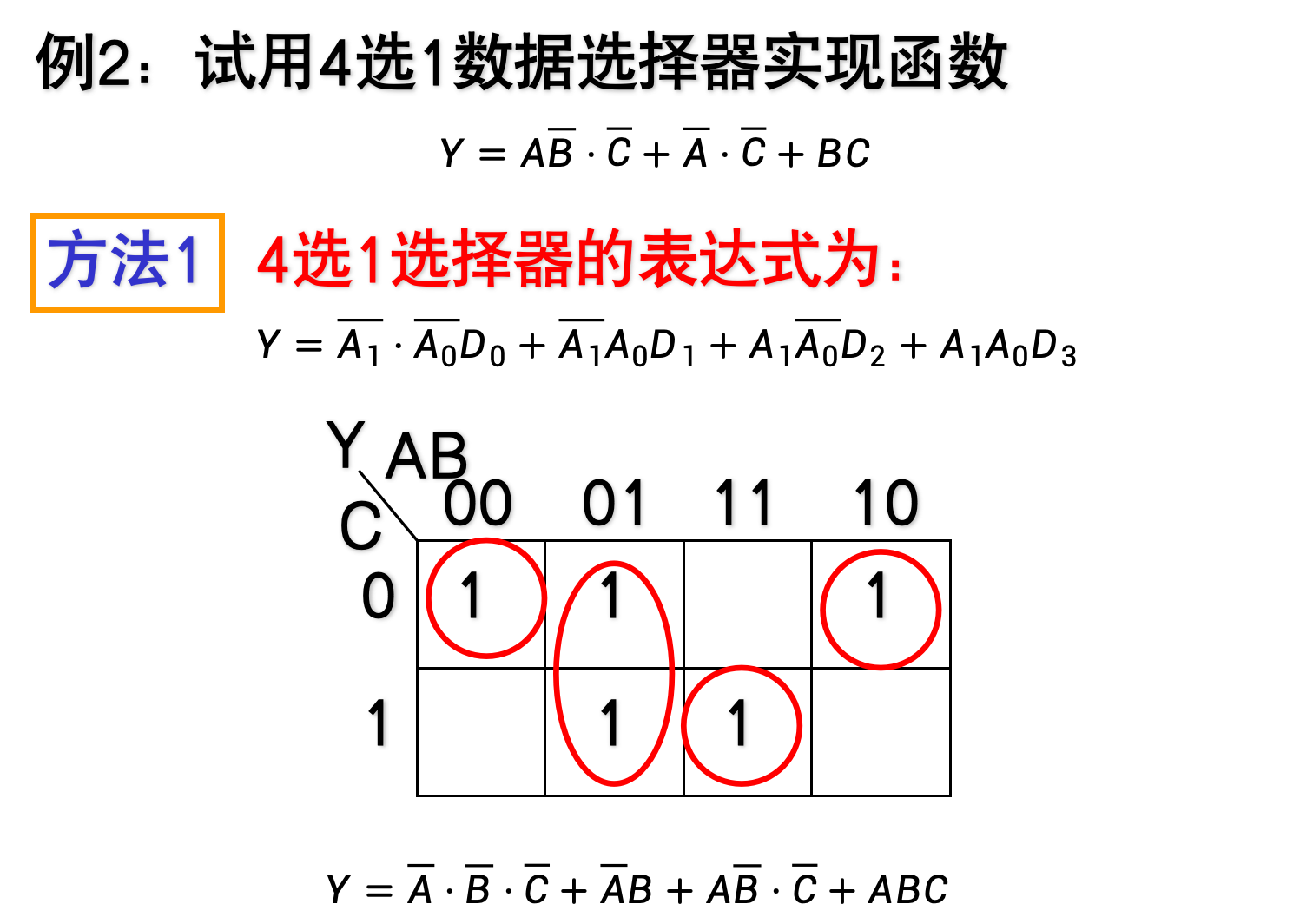

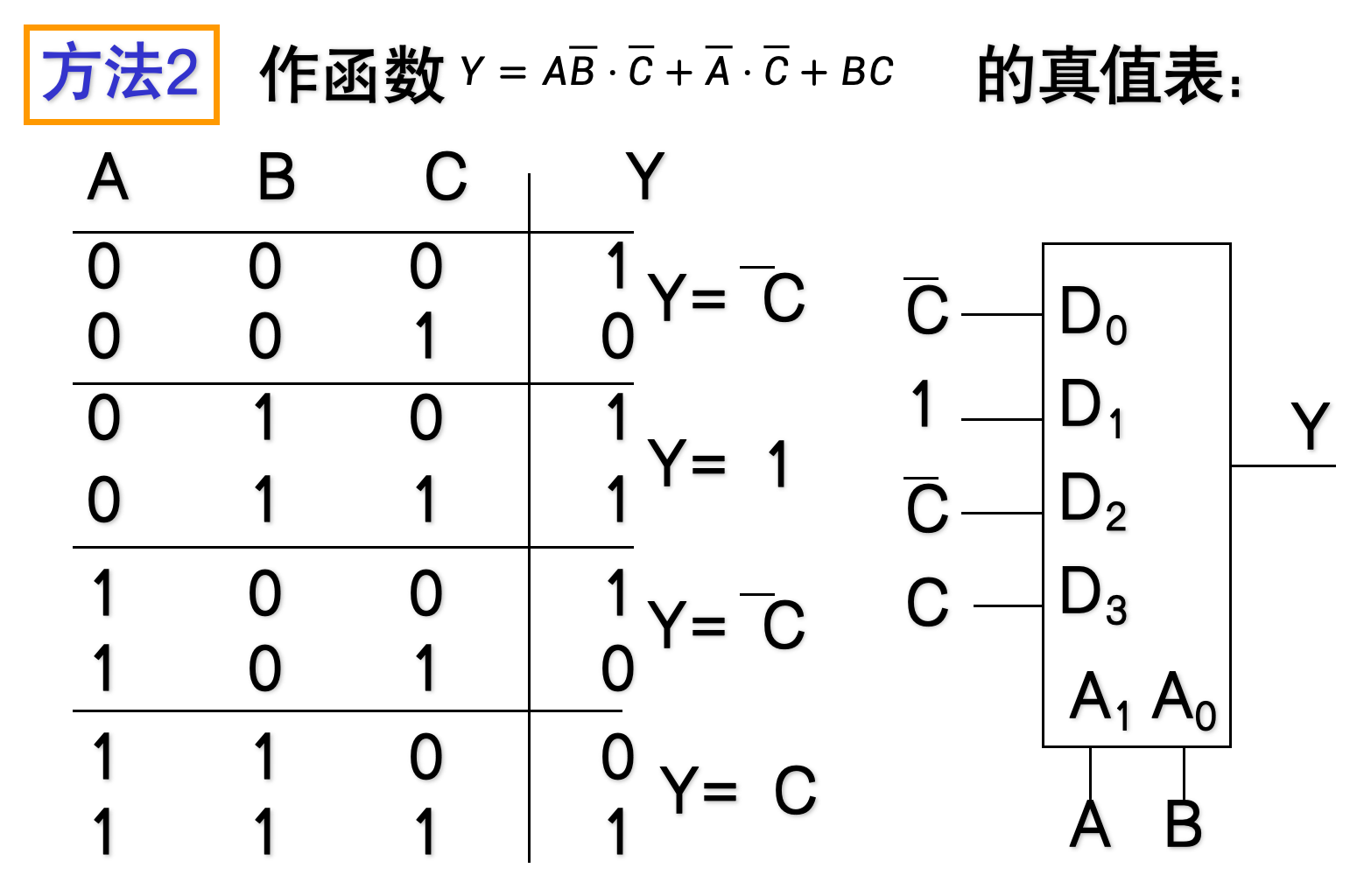



- 1W对应的输出是F1的输出、2W对应的输出是F2的输出
-
4.4 组合逻辑电路的险象
4.4.1 竞争
-
概述
-
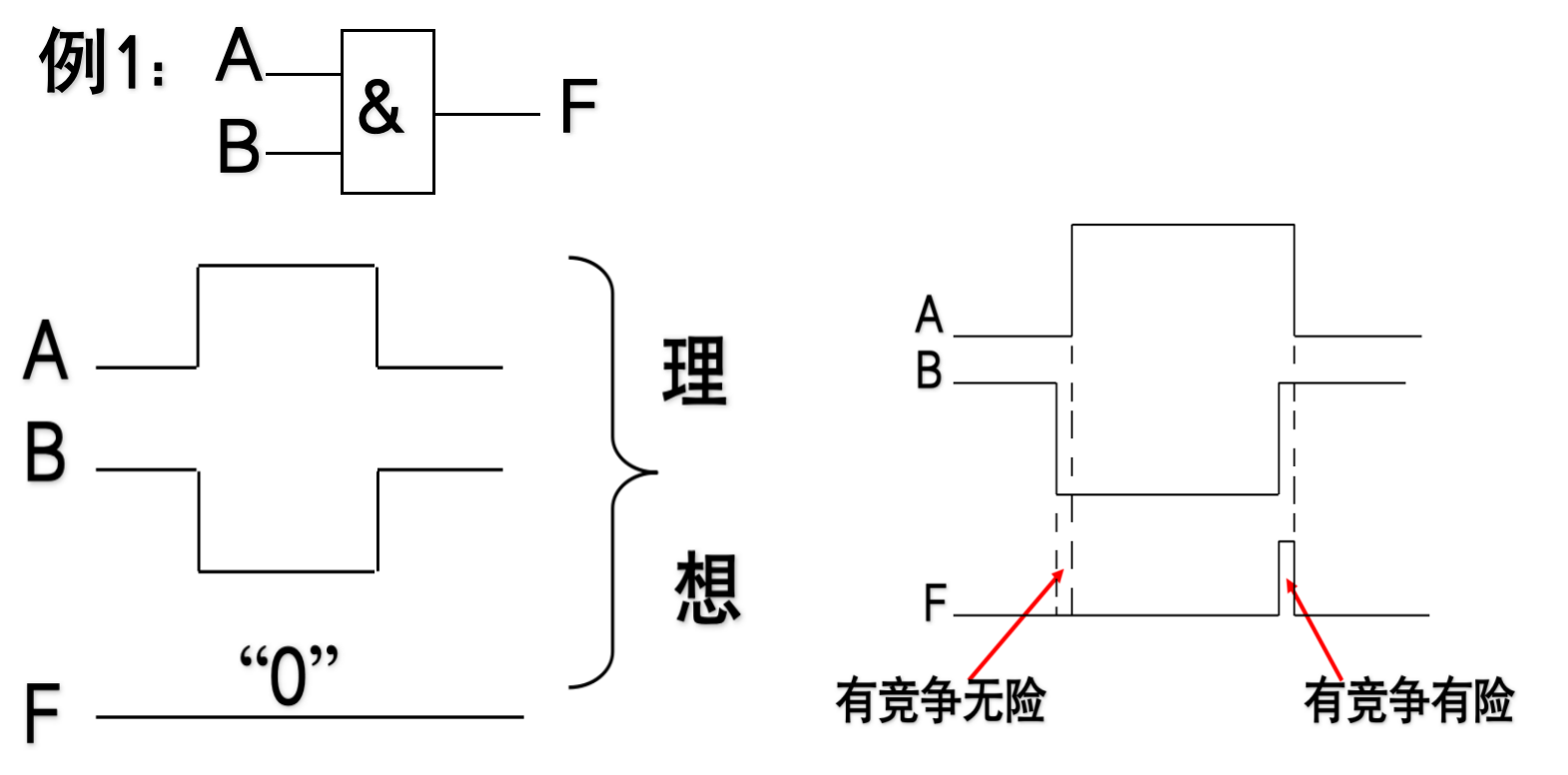
由于电路中各个信号通过的路径不同,当加到某个门电路的两个信号同时向相反方向变化时:
- 变化时间有微小差异。
- 信号边沿变化时间存在差异。
-
这就是组合电路的竞争现象。
-
4.4.2 冒险
-
由于存在竞争,使电路的输出出现瞬间的逻辑错误称为险象。工程上也称为毛刺。
4.4.3 险象的分类
-
按输出是否变化分类
-
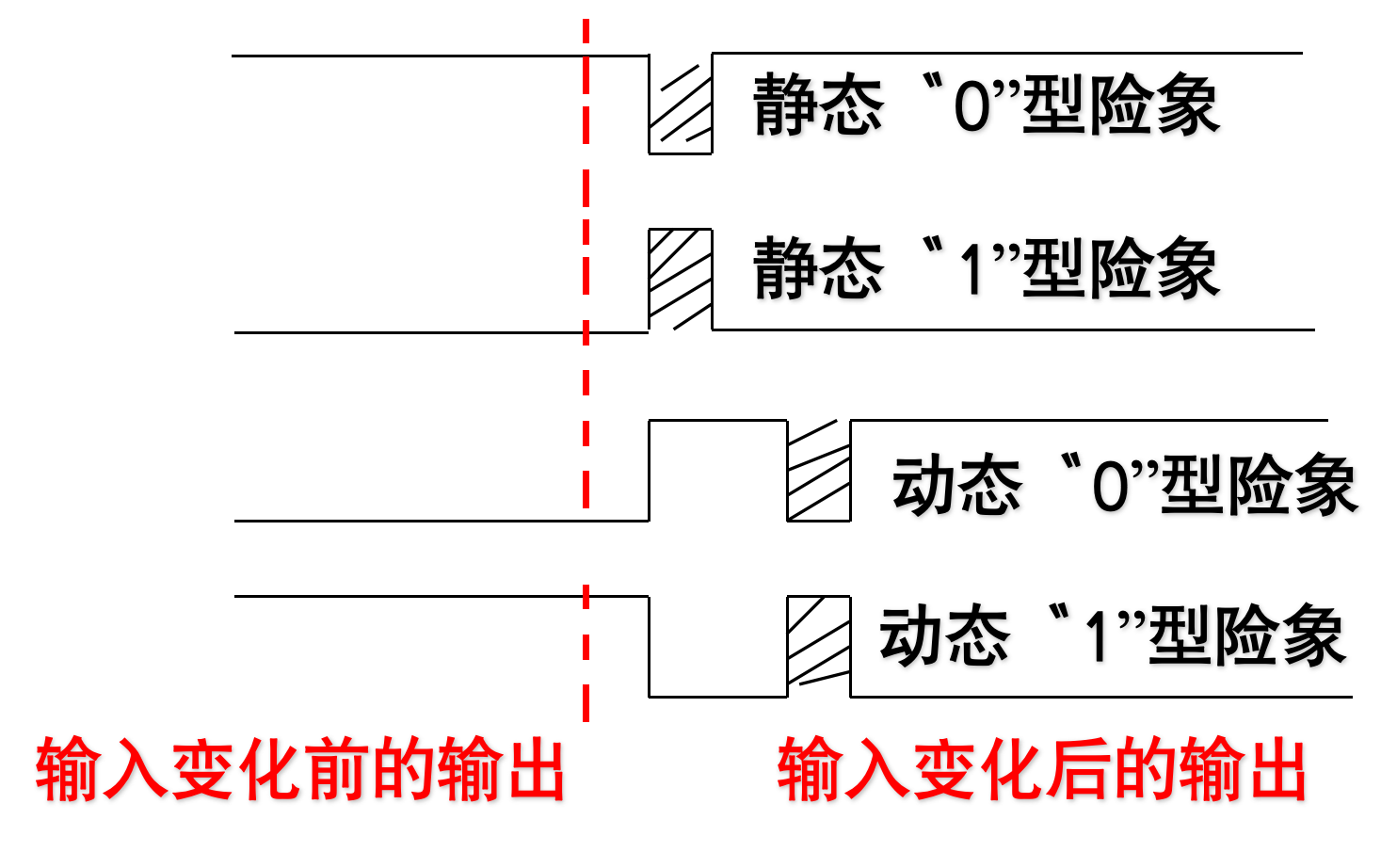
若在输入变化而输出不应发生变化的情况下,输出产生的险象,称为静态险象。
-
若在输入变化而输出应该发生变化的情况下,输出在变化过程中产生的险象,称为动态险象。
-
-
按错误信号类型分类
- 若错误输出为负脉冲称"0"型险象。
- 若错误输出为正脉冲称"1"型险象。
4.4.4 险象判断
4.4.4.1 代数法
-
在逻辑表达式,令除了某个逻辑变量(如变量 A A A)及该变量的非(如 A ˉ \bar A Aˉ )以外的其它变量为某个恒定值后,若出现 A + A ˉ A+\bar A A+Aˉ 或 A ⋅ A ˉ A \cdot \bar A A⋅Aˉ ,则必然存在险象。
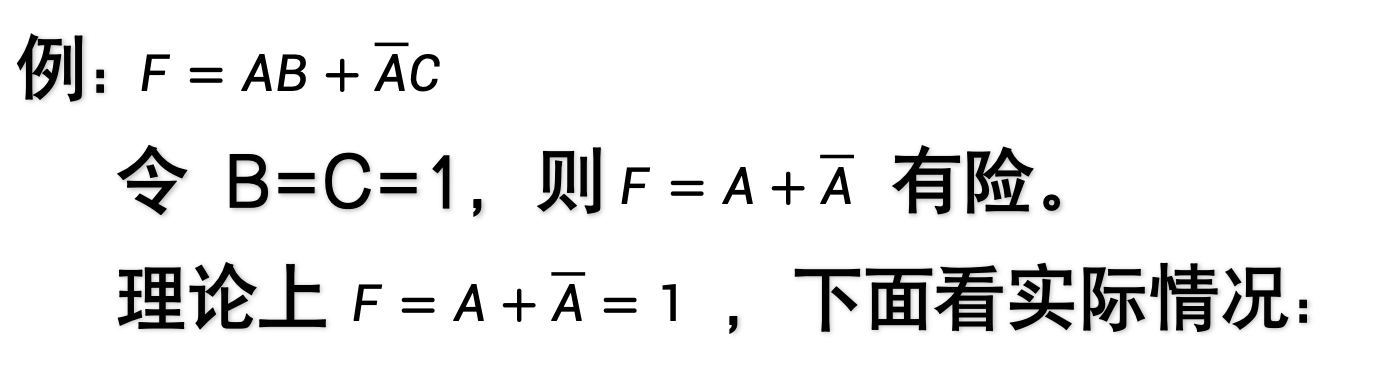
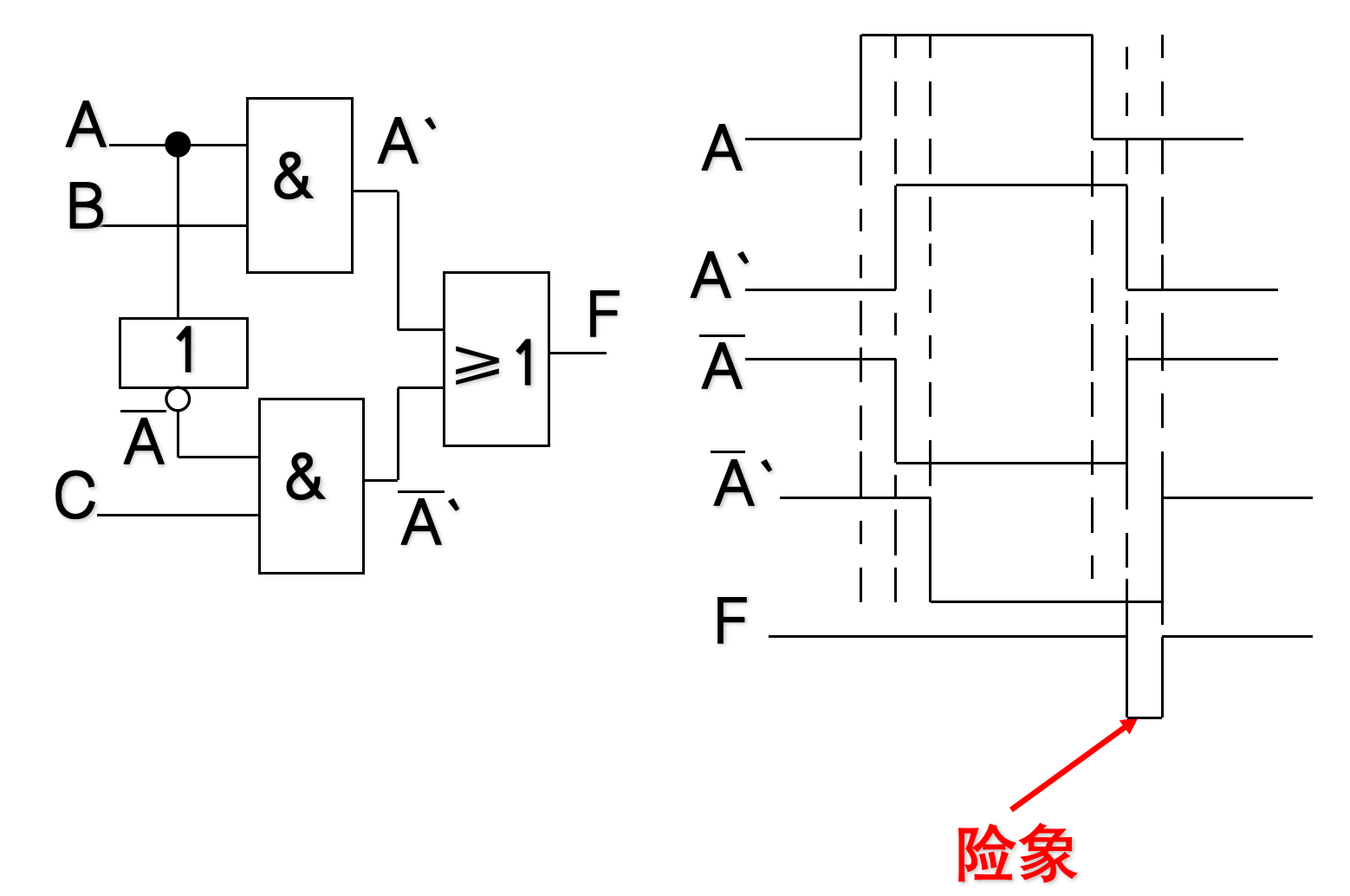
4.4.4.2 卡诺图判断法
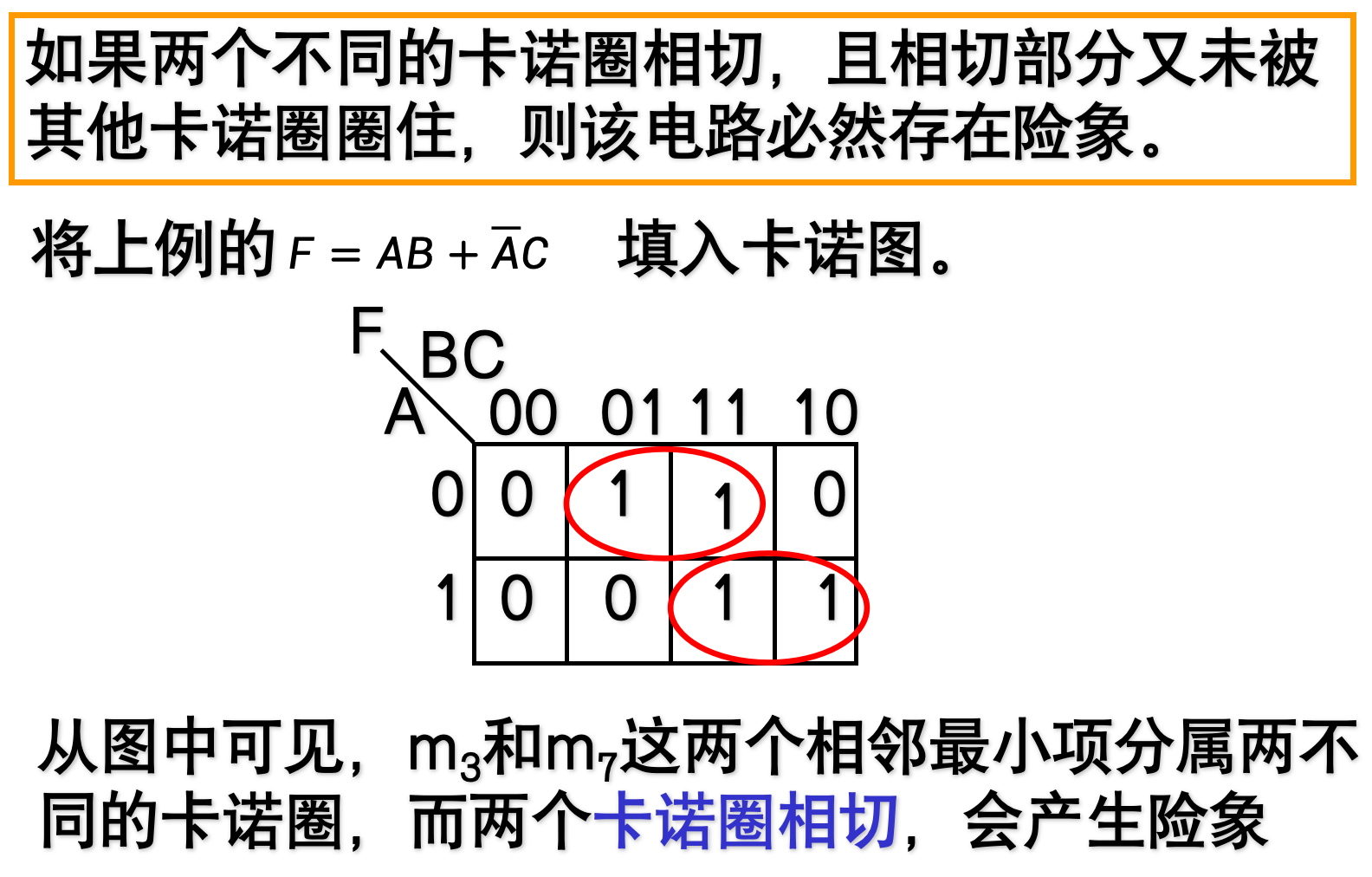
4.4.5 险象的消除或减弱
-
引入封锁脉冲(由于同步问题不易实现)
-
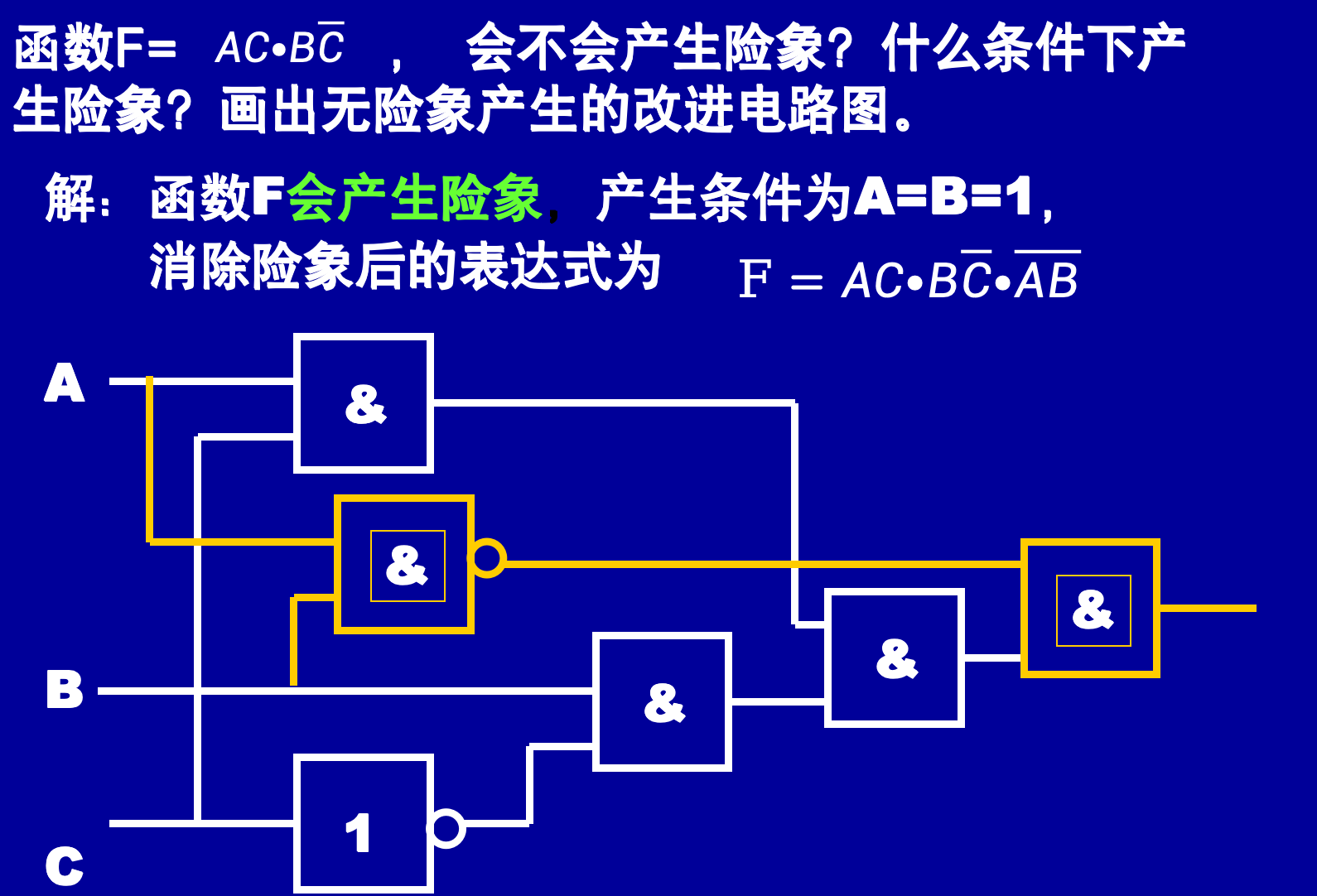
增加冗余项
- 如 F = A B + A ˉ C + B C F = AB +\bar AC +BC F=AB+AˉC+BC,则当B=C=1时或门输出恒为"1",消除了"0"险象。
- 冗余项的加法:把条件以某种方式加入表达式中,使得条件成立时,表达式值不变;条件不成立时,也不影响表达式的结果。
-
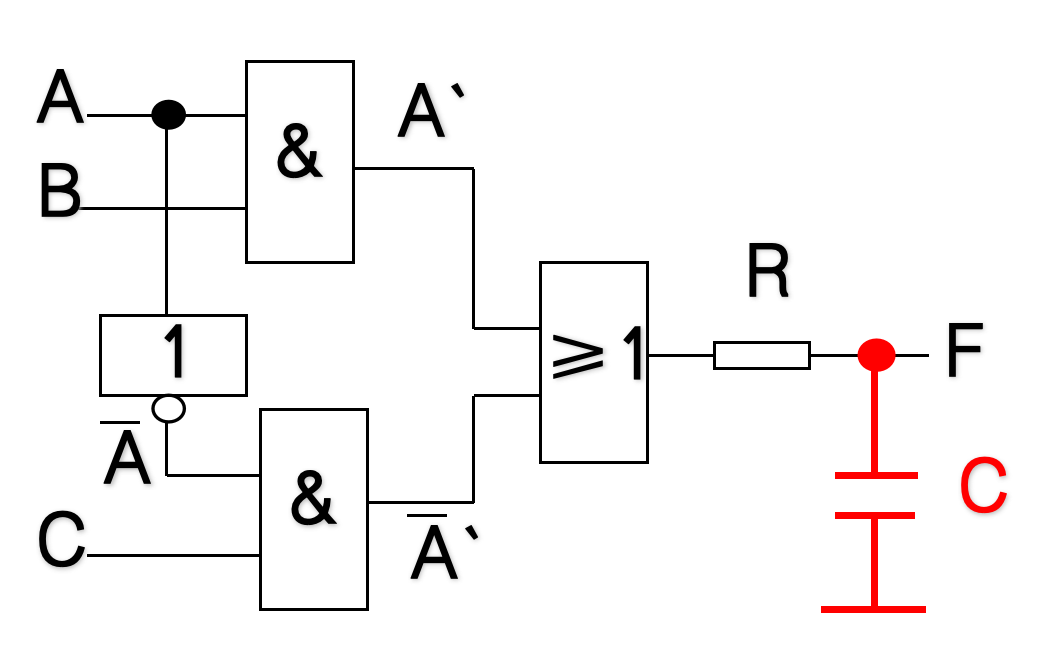
输出加低通滤波电路
-
险象所产生的干扰脉冲一般都很窄,所以可以在电路的输出端并接一个小电容来减弱干扰脉冲。
-