OpenAI 挑战了一项被视为不可能的任务:通过将Transformer的权重在训练过程中压缩至接近绝对零值,强制模型仅依赖极少数连接执行全部计算。
这一极端条件下,模型内部负责逻辑推理的"计算电路"首次实现了可分离、可验证的显性化呈现。
这堪称人类迄今为止对Transformer工作机制最深刻的洞察突破。
在大型模型主导的时代,Transformer的不可解释性已成为普遍认知。无论是注意力头分析、激活模式追踪,还是反事实样本构建,传统研究方法在dense Transformer的层间交织中均遭遇瓶颈------数万条通道的密集交互使得内在结构难以辨识。
OpenAI的《Weight-sparse Transformers Have Interpretable Circuits》研究采取了截然相反的思路:并非对dense模型进行事后解析,而是在训练初期就抑制其dense化倾向。
通过维持训练全程的接近零权重状态,模型被迫在最小连接集内完成计算任务。当冗余路径被极致压缩后,那条支撑推理的核心因果链------即论文中定义的"计算电路"(circuit)------便以清晰可追溯的形态浮现。
更具突破性的是,这些电路不仅能够完整映射计算流程,其因果有效性还可通过实验验证。研究者能够独立调控电路节点、预判dense Transformer的失效情形,甚至引导dense模型产生与稀疏电路一致的响应。
该研究揭示了一个颠覆性观点:Transformer的不可解释性并非其固有属性,而是源于传统训练方法未能提供可解释的成长路径。

论文标题:
Weight-sparse transformers have interpretable circuits
01
方法
若将dense Transformer比作一个路网密布的超级都会,OpenAI的策略则是在训练初期封闭绝大多数支线,仅保留主干道。所有计算必须沿这些核心通道流动,而承担关键任务的路径也因此被凸显出来。
该方法可分解为三个核心步骤:训练初期维持极稀疏性、引导电路结构自然浮现,最终实现对dense模型的逆向解析。
更多AI大模型学习视频及资源,都在智泊AI。
1.1 训练时强制稀疏:从源头上避免 dense
OpenAI 摒弃了传统"先密集训练后剪枝"的常规路径,创新性地设定:所有权重矩阵在训练全周期内均维持固定数量的非零参数。
这种机制使网络层持续执行三个标准化操作:
forward传播:执行标准矩阵运算
反向传播:按梯度更新参数
参数投影:仅保留绝对值最大的k个权重,其余强制置零
整个模型始终保持高度稀疏特性,由此产生三个显著优势:
抑制冗余神经连接的生长
降低特征功能的相互干扰
促使特定任务聚焦于有限激活通路
该训练框架在论文中通过可视化流程图进行了系统阐述,其结构清晰展示了上述动态过程的核心逻辑。
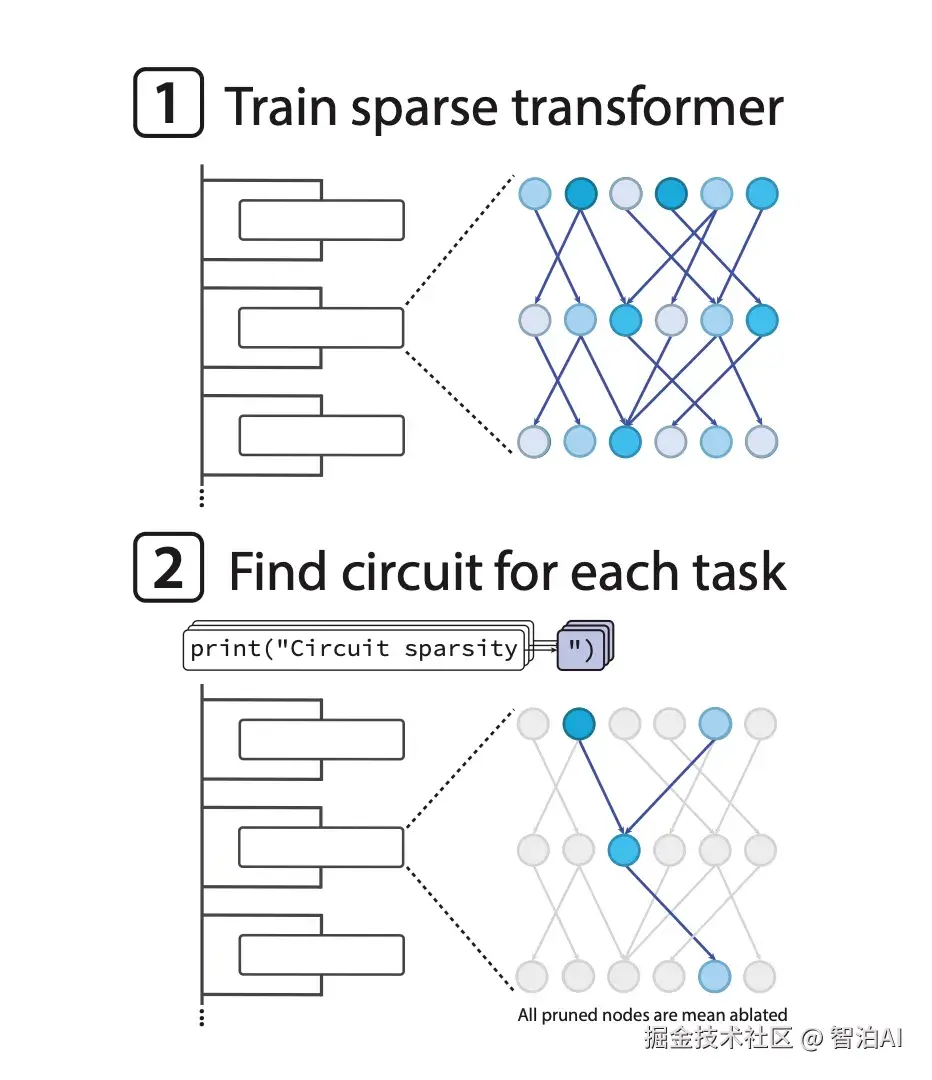
图1. 从稀疏训练到抽取最小计算电路的整体流程。模型在全程保持极端稀疏,通过节点剪枝得到完成任务所需的最小结构。
1.2 让模型自己暴露关键节点
为揭示最小电路的工作机制,研究者在residual channel、attention输入输出等关键节点引入gate结构。训练过程中,模型会自主激活部分gate而关闭其余部分,这一动态过程清晰表明:执行该任务时,仅需依赖特定路径即可完成。
gate 的形式写成:
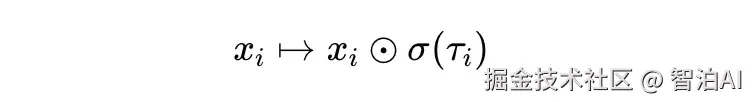
细节不必深究,只需知道:最终被 gate 激活的节点,就是模型真正用到的因果单元。
在字符串闭合引号任务中,稀疏模型最终只留下 12 个节点和 9 条边(见下图),整个推理链像蓝图一样干净。
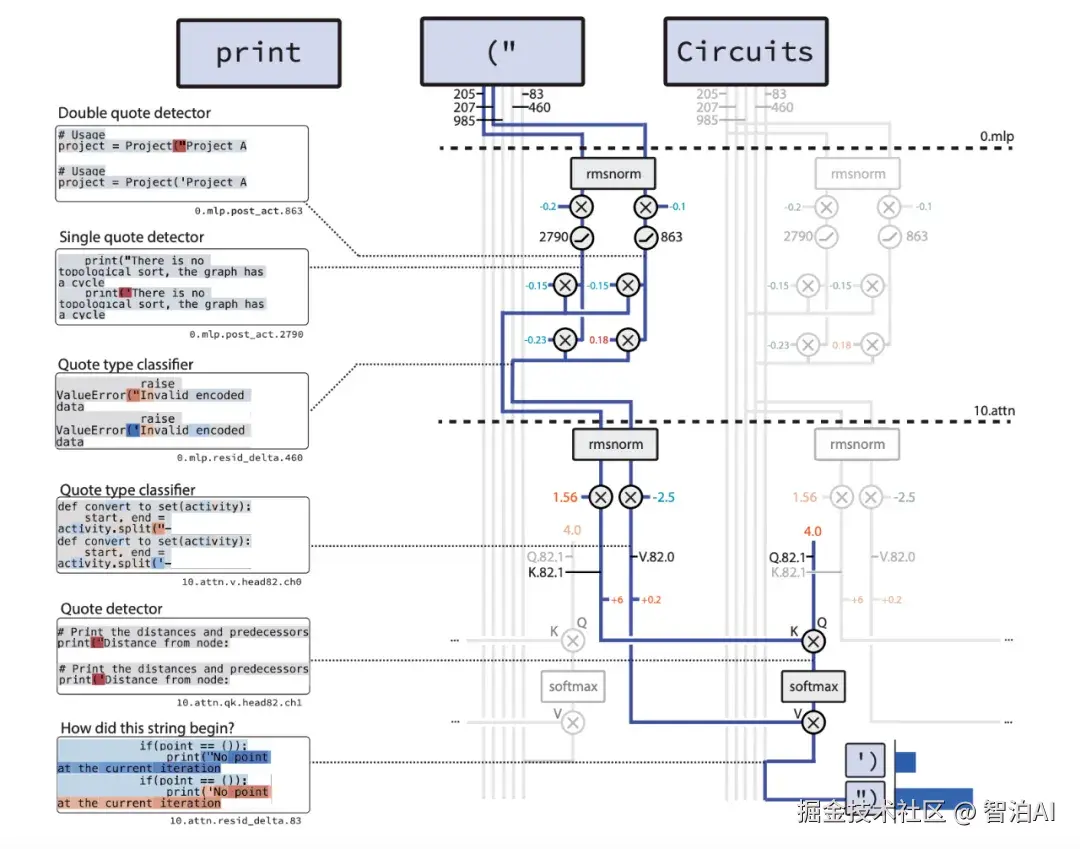
图2. 字符串闭合引号任务所抽取的计算电路
1.3 更复杂的推理:嵌套括号深度
嵌套括号的处理复杂度显著高于引号,然而稀疏模型生成的电路结构始终保持有序。当检测到字符"[ "时,模型会初始化一个"开括号特征",随后通过单一注意力头对该特征的历史值进行全局平均聚合。聚合结果的差异对应不同的嵌套层级,最终输出位置将依据层级判断生成"]"或"]]"。
在dense模型中,此类机制会分散至多个注意力头与大量残差通道中,相互交织难以辨识;而在稀疏模型中,该过程呈现为一条清晰且稳定的路径。
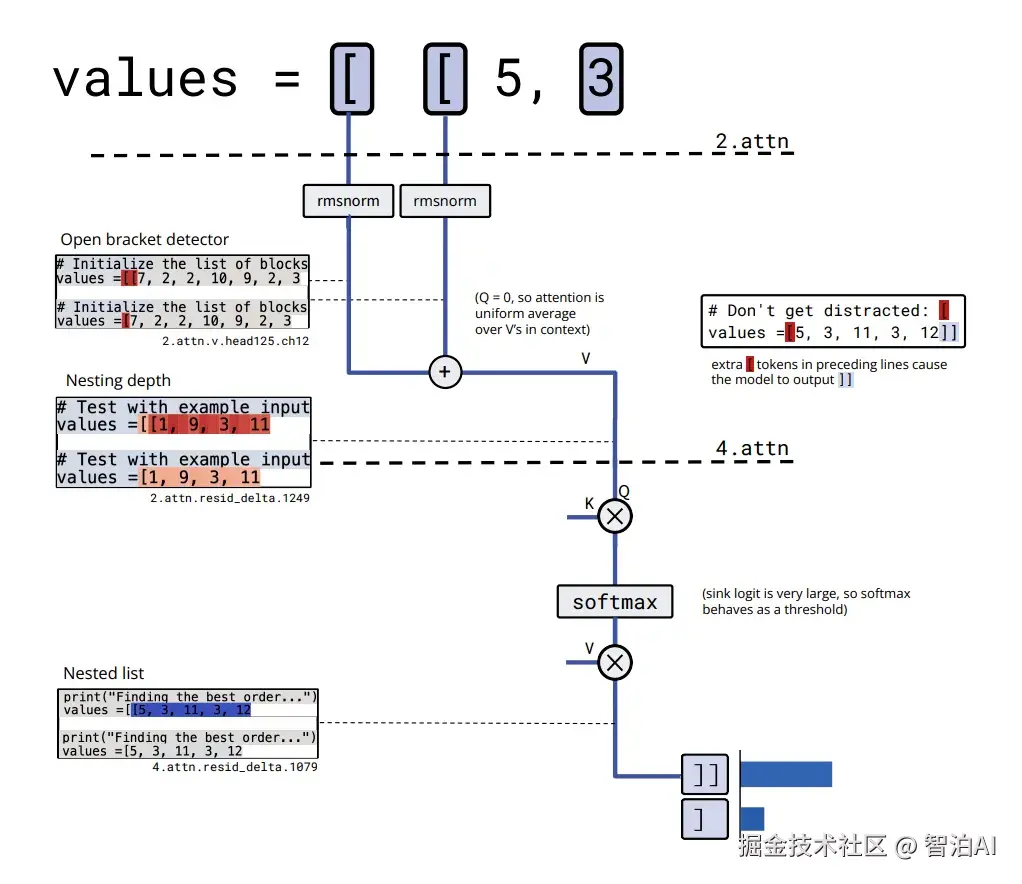
图3. 稀疏模型计算括号深度的电路示意
1.4 Bridge:让稀疏模型解释 dense Transformer
稀疏模型因其结构透明性而易于理解,然而在实际生产环境中,dense模型才是我们关注的核心目标。Bridge的设计初衷正是建立两者间的关联,使稀疏电路能够作为dense模型的"可解释性接口"。
该实现流程包含两个关键阶段:
逆向转换:将dense模型各层激活值对应到稀疏表示空间(dense → sparse)
正向转换:将稀疏空间的激活结果重新映射回dense模型(sparse → dense)
并用 NMSE loss 对齐:
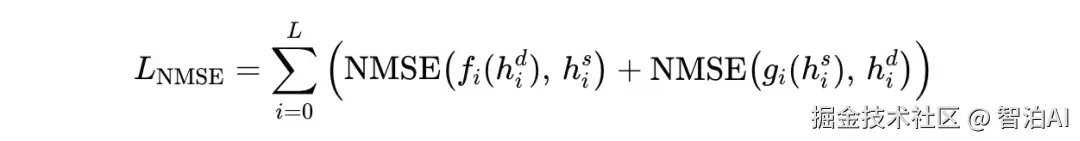
对应结构在下图中给出:
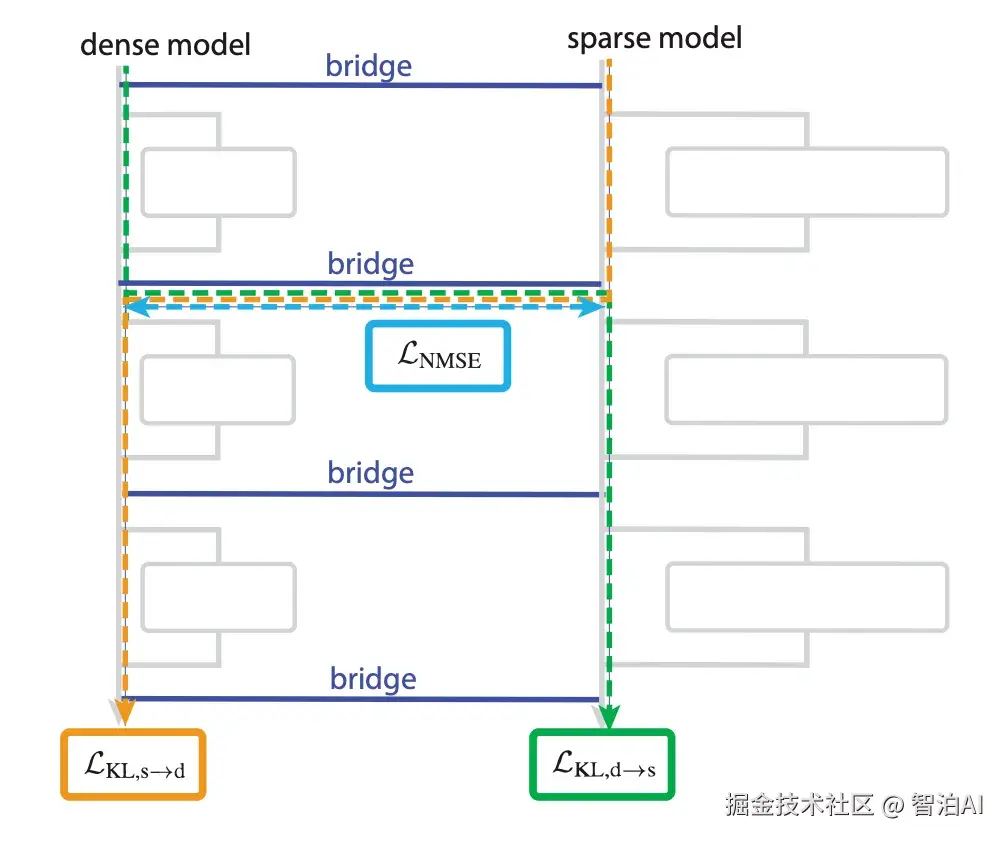
图4. Bridge 使用线性映射对齐 sparse 与 dense 的中间激活,使得两者可以互相转换并保持混合路径的性能。
02
实验
当电路被提取完成后,一个关键问题立即浮现:该路径是否确为模型的实际依赖路径?后续实验的核心目标正是对这一问题的全面验证。
2.1 电路规模的规律性
dense Transformer提取的最小电路尺寸波动显著,针对相同任务时数值差异极大,缺乏明显规律性。研究中将dense模型与稀疏模型的规模数据绘制于同一图表中。dense模型的数据点分布较为分散,而稀疏模型的数据点则高度集中,近似沿一条稳定的带状区域分布。
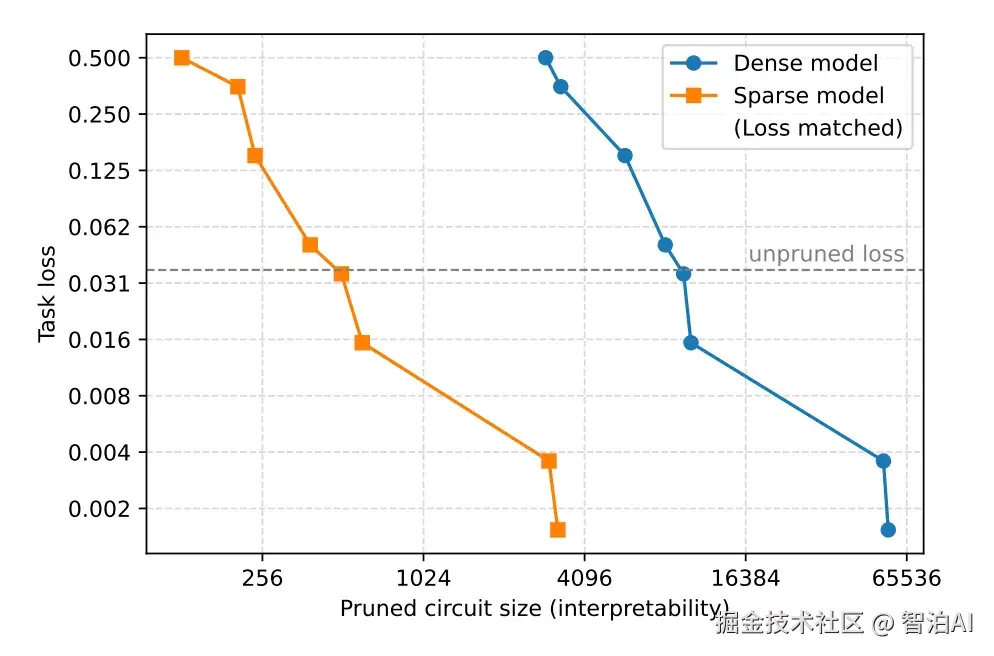
图5. 稀疏模型在所有任务上的最小电路规模显著更小,在相同损失下约比 dense 模型小 16 倍。
稀疏结构不仅减少参数,也让任务分工更稳定。
2.2 模型越大,电路反而更小
稀疏模型随规模扩展呈现性能提升趋势,而最小电路规模持续减小;dense模型则相反:规模扩增伴随结构复杂化程度加剧。
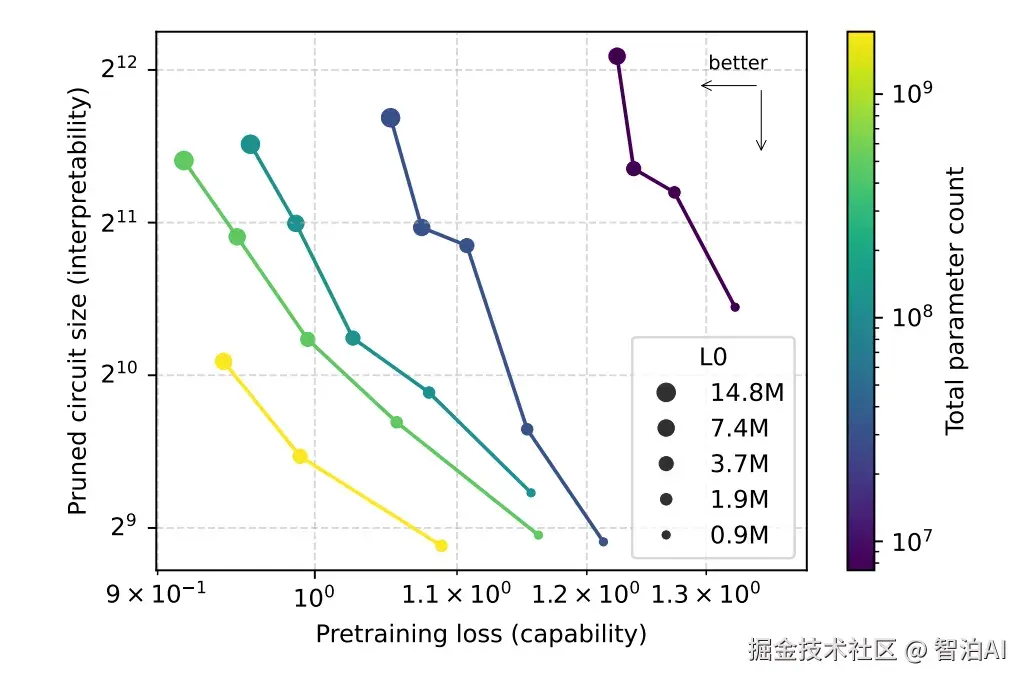
图6. 更大的稀疏模型拥有更小的计算电路与更高性能
这组结果说明:可解释性与能力并非一定对立,有可能同时提升。
2.3 稀疏电路能推断 dense 模型的错误
在嵌套括号任务中,稀疏电路的研究表明:模型通过平均注意力机制对全部[进行聚合计算。当输入序列长度增加时,平均值的统计效应会减弱,导致深层特征信息逐渐衰减。基于此观察,稀疏电路理论推测:传统dense模型在处理长序列时,可能将实际深度为2的结构误判为深度1的特征表示。
为验证这一假设,OpenAI设计了针对长序列的对抗性测试实验。实验数据显示,dense模型的识别错误率会随着序列长度增长而显著提高,该结果与稀疏电路的理论预测高度吻合。
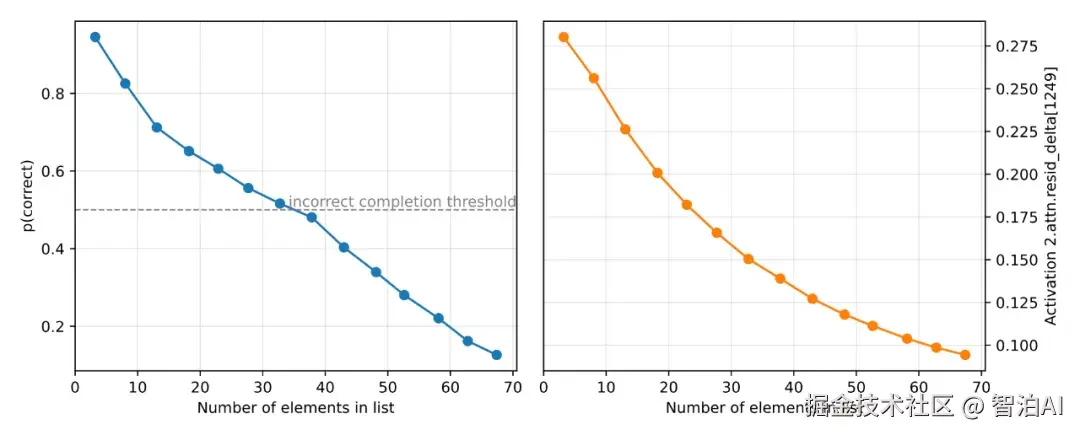
图7. dense 模型在长序列上出现与稀疏电路预测一致的 context dilution 错误模式。
这是一个很典型的例子:结构化解释可以推断模型的失败。
2.4 电路可以影响 dense 模型
最终实验验证了更显著的效果:通过Bridge机制,经过对齐的稀疏电路能够对dense Transformer的输出产生直接调控作用。
在单双引号('与")的区分任务中,研究人员通过修改稀疏模型中表征引号差异的通道激活状态,并将其参数重新注入dense模型,观察到dense模型的输出概率呈现连续且稳定的变化趋势。
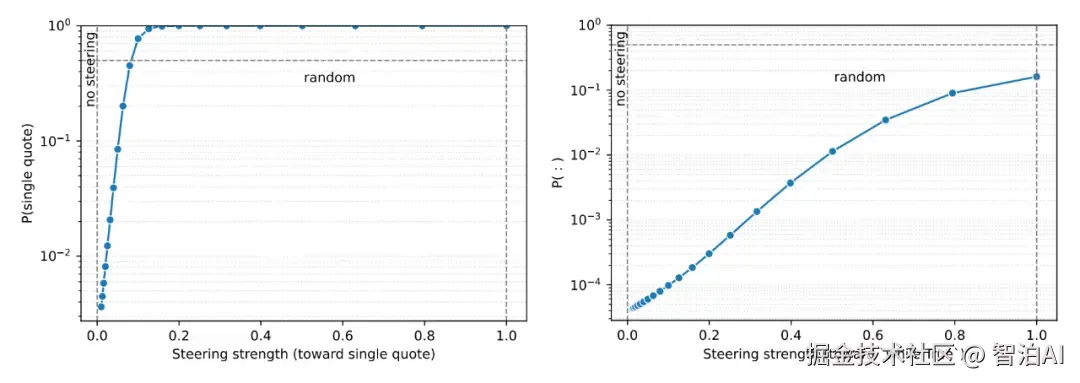
图8. 通过 Bridge,对稀疏模型的可解释激活进行调整后,可连续影响 dense 模型的输出概率。
这说明电路不仅能解释 dense 行为,还能驱动 dense 行为。
03
结语
这篇论文提出了一种创新的可解释性方法论:并非对dense Transformer进行事后解析,而是通过训练机制使其自发形成可解释的内在架构。
在极端稀疏的权重限制条件下,Transformer的功能分布从全局扩散转变为聚焦于有限关键路径。这些路径------即计算电路------具备三大特性:
可提取性:能够被完整分离
可理解性:逻辑关系可被人类认知
可干预性:可反向调控dense模型的决策行为
实验验证表明,通过稀疏训练获得的计算电路:
呈现稳定的因果关联
能准确预判dense模型的行为模式
具备双向调控能力(既可预测又可修正输出)
该研究为AI发展开辟了新路径:在模型规模持续扩大的趋势下,我们应当同步探索结构化组织、可控性和可验证性的内在机制,而非单纯追求参数密度的提升。
Transformer架构首次显露出了其内在结构的可辨识性,这一突破为后续研究提供了重要基础。
更多AI大模型学习视频及资源,都在智泊AI。