字符串 和 队列 + 宽搜
字符串
最长公共前缀
题目解析:就是这个String数组中,最长的公共前缀
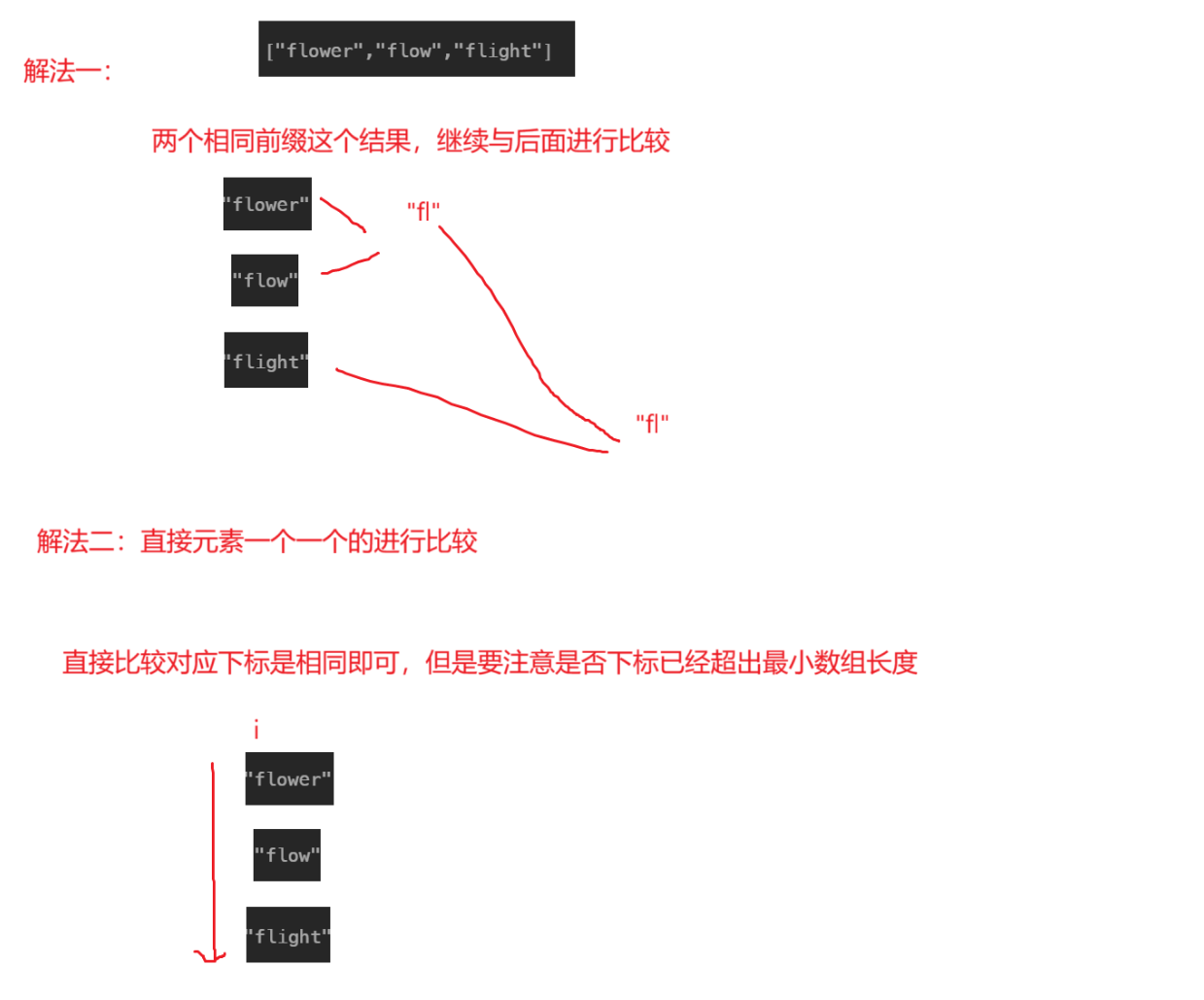
解法一:直接两两进行前缀和求解,这样得到的新结果不断和后面继续进行比较
解法二:每次都将数组所有元素对应下标对应字母求出来进行比较
时间复杂度:O(m * n)
java
//解法一:
class Solution {
public String longestCommonPrefix(String[] strs) {
//两两进行比较
String ret = strs[0];
for(int i = 1; i < strs.length; i++){
ret = findComment(ret,strs[i]);
}
return ret;
}
public String findComment(String str1,String str2){
int i = 0;
int minlen = Math.min(str1.length(),str2.length());
while(i < minlen){
if(str1.charAt(i) == str2.charAt(i)){
i++;
}else{
return str1.substring(0,i);
}
}
return str1.substring(0,i);
}
}
java
//解法二:
class Solution {
public String longestCommonPrefix(String[] strs) {
//两两进行比较
for(int i = 0; i < strs[0].length();i++){
char ch = strs[0].charAt(i);
for(int j = 1;j < strs.length; j++){
//当元素不相等,或者超出长度就返回
if(i == strs[j].length() || strs[j].charAt(i) != ch){
return strs[0].substring(0,i);
}
}
}
//全部都是公共前缀
return strs[0];
}
}时间复杂度:O(m * n)
空间复杂度:O(1)
最长回文子串

题目解析 :找出这个字符串中的最长回文子串
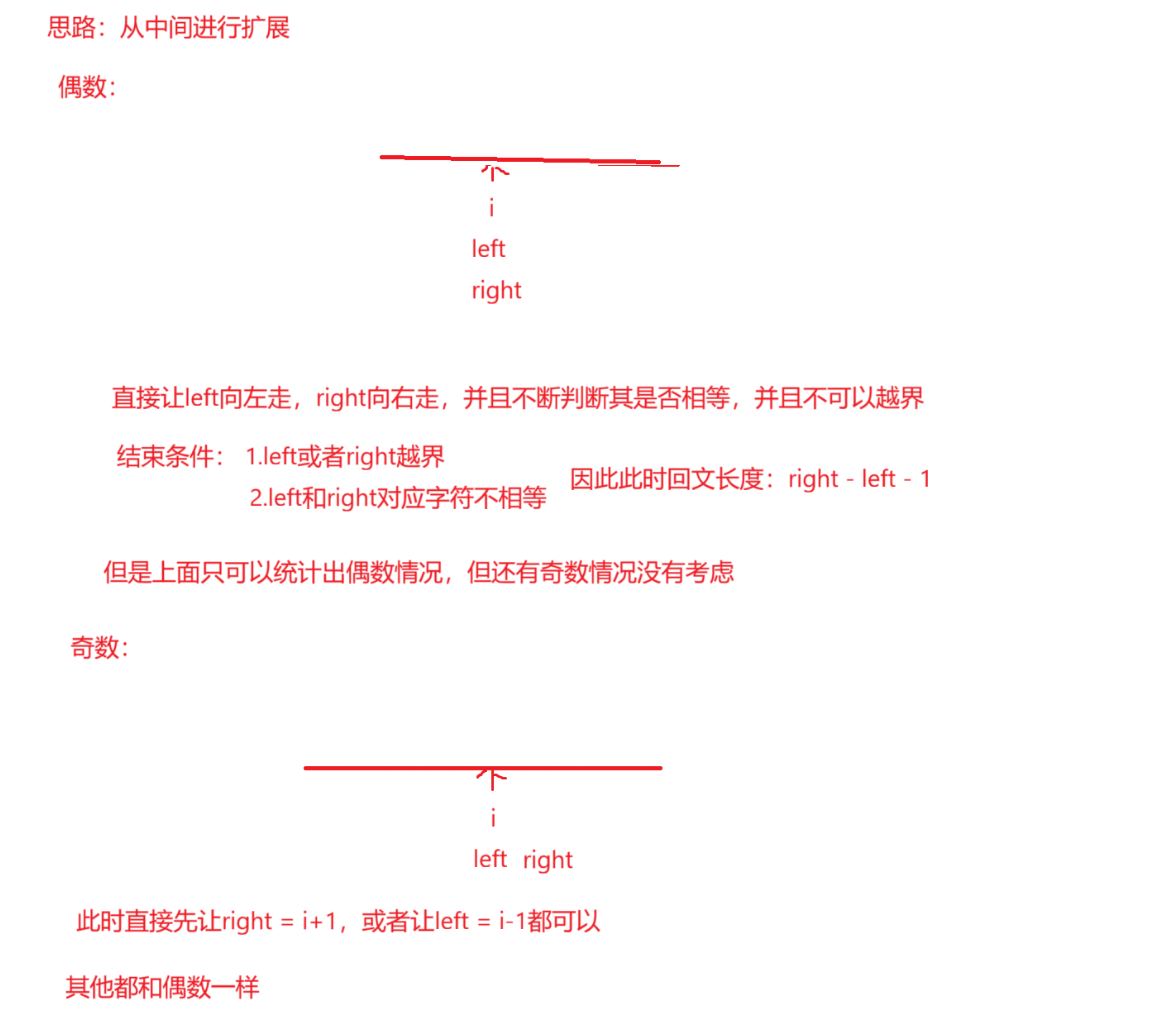
解法 :中心扩展算法,找到数组中一个i下标,有left和right下标不断向左右进行扩展,但是此时要分奇数和偶数偶数:就是left = right = i,left向左扩展,right向右扩展
奇数:就是,left = i , right = i+1或者 left = i-1;right = i,left向左扩展,right向右扩展
但是注意这里当不满足回文条件或者越界,此时left+1和right-1才是真正回文区间
并且此时我们只要找出最长长度的回文子串,记录一下下标即可
java
class Solution {
public String longestPalindrome(String s) {
//找出最长回文子串
//直接可以先确定一个中心点,不断向两边进行扩展
int begin = 0;
int len = 0;
for (int i = 0; i < s.length(); i++) {
int left = i;
int right = i;
//奇数
while (left >= 0 && right < s.length() && (s.charAt(left) == s.charAt(right))) {
//继续扩展
left--;
right++;
}
if (len < (right - left - 1)) {
begin = left + 1;
len = right - left - 1;
}
//偶数
left = i;
right = i + 1;
while (left >= 0 && right < s.length() && (s.charAt(left) == s.charAt(right))) {
//继续扩展
left--;
right++;
}
if (len < (right - left - 1)) {
begin = left + 1;
len = right - left - 1;
}
}
//前闭后开
return s.substring(begin,begin+len);
}
}时间复杂度:O(n ^2)
空间复杂度:O(1)
二进制求和

题目解析 :计算两个字符串相加,和正常两个整数相加一样,因此计算要先将其转成整数,再进行计算
模拟:模拟加法过程即可 ,要记住进位

java
class Solution {
public String addBinary(String a, String b) {
//直接对应位相加即可,并记录其进位
StringBuilder ret = new StringBuilder();
int cur1 = a.length() - 1;
int cur2 = b.length() - 1;
int t = 0;
while(cur1 >= 0 || cur2 >= 0 || t != 0){
if(cur1 >= 0){
t += a.charAt(cur1) - '0';
}
if(cur2 >= 0){
t += b.charAt(cur2) - '0';
}
//将其进行拼接
ret.append((char) (t % 2 + '0'));
t /= 2;
cur1--;
cur2--;
}
return ret.reverse().toString();
}
}字符串相乘

题目解析 :就是乘法运算
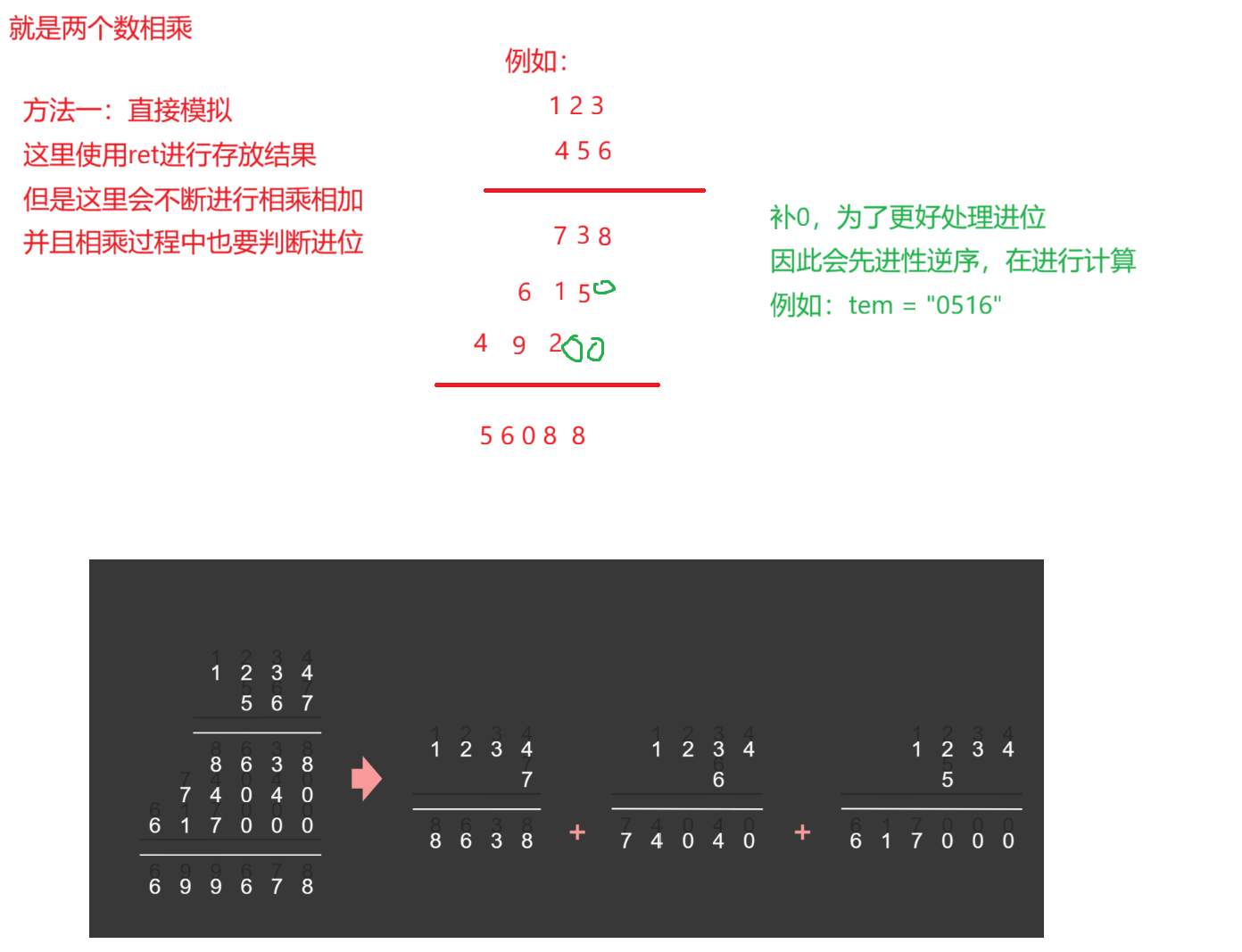
解法一 :正常列竖式运算,运算过程中会不断相乘进位相加进位繁琐
解法二:先无进位相乘相加,最后再处理进位

java
//解法一
class Solution {
public String multiply(String num1, String num2) {
if (num1.equals("0") || num2.equals("0")) {
return "0";
}
String ret = "0";
int m = num1.length(), n = num2.length();
for (int i = n - 1; i >= 0; i--) {
StringBuffer tem = new StringBuffer();
int t = 0;//进位
//补0
for (int j = n - 1; j > i; j--) {
tem.append(0);
}
int y = num2.charAt(i) - '0';
for (int j = m - 1; j >= 0; j--) {
int x = num1.charAt(j) - '0';
int result = x * y + t;
tem.append(result %10);
t = result / 10;//更新进位
}
//处理最后一个进位
if (t != 0) {
tem.append(t % 10);
}
//此时就要进行相加
ret = addStrings(ret, tem.reverse().toString());
}
return ret;
}
//计算两个相加
public String addStrings(String num1,String num2){
int m = num1.length()-1;
int n = num2.length()-1;
StringBuffer ret = new StringBuffer();
int t = 0;
while(m >= 0 || n >= 0){
if(m >= 0){
t += num1.charAt(m) - '0';
}
if(n >= 0){
t += num2.charAt(n) - '0';
}
ret.append(t % 10);
t /= 10;
m--;
n--;
}
//处理最后一个进位问题
if(t != 0){
ret.append(t % 10);
}
return ret.reverse().toString();
}
}
java
//解法二
class Solution {
public String multiply(String num1, String num2) {
//如果有0,其结果就是0
if(num1.equals("0") || num2.equals("0")){
return "0";
}
//1.先无进位相加相乘
int m = num1.length();
int n = num2.length();
//存放结果
int[] tem = new int[m + n - 1];
for(int i = m - 1;i >= 0;i--){
//从后面确定一个数,与另一个数进行相乘
for(int j = n - 1;j >= 0;j--){
//存放到对应下标上,此时存放的结果是反过来的
tem[m + n - 2 - i - j] += ( num1.charAt(i) - '0') * (num2.charAt(j) - '0');
}
}
//2进位处理
int t = 0;
int cur = 0;
StringBuffer ret = new StringBuffer();
//进行进位处理,直接对上面数组处理即可
while(cur < m + n -1 ){
t += tem[cur++];
ret.append(t % 10);
t /= 10;
}
if(t != 0){
ret.append(t % 10);
}
//逆置,此时逆置后可能会出现
return ret.reverse().toString();
}
}队列+宽搜
N叉树的层序遍历
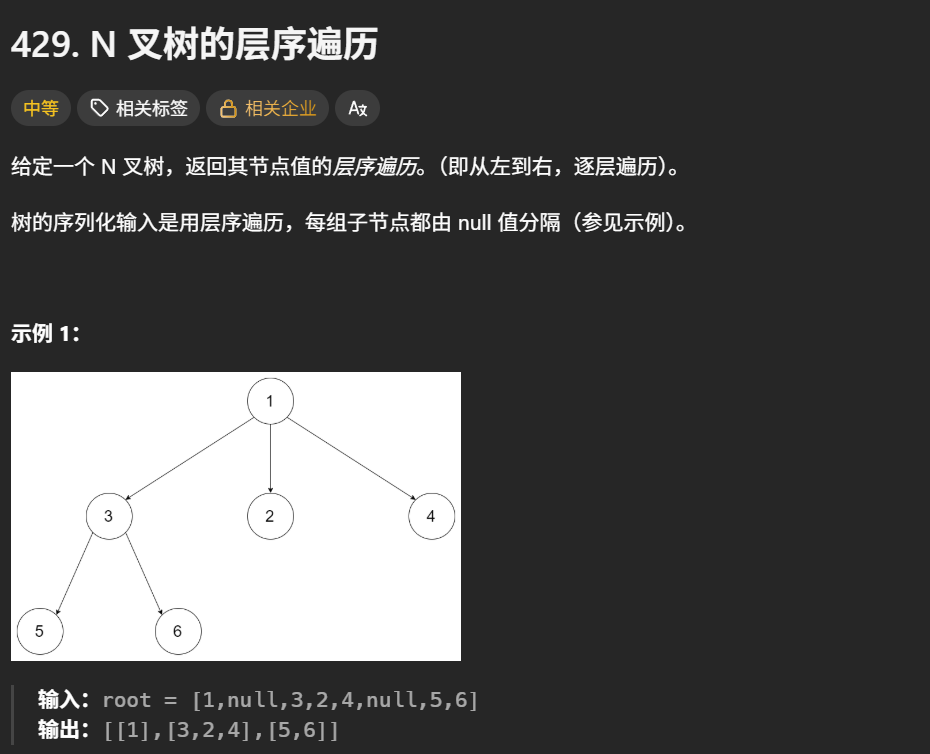
题目解析:就是层序遍历,从上到下,从左到右进行遍历
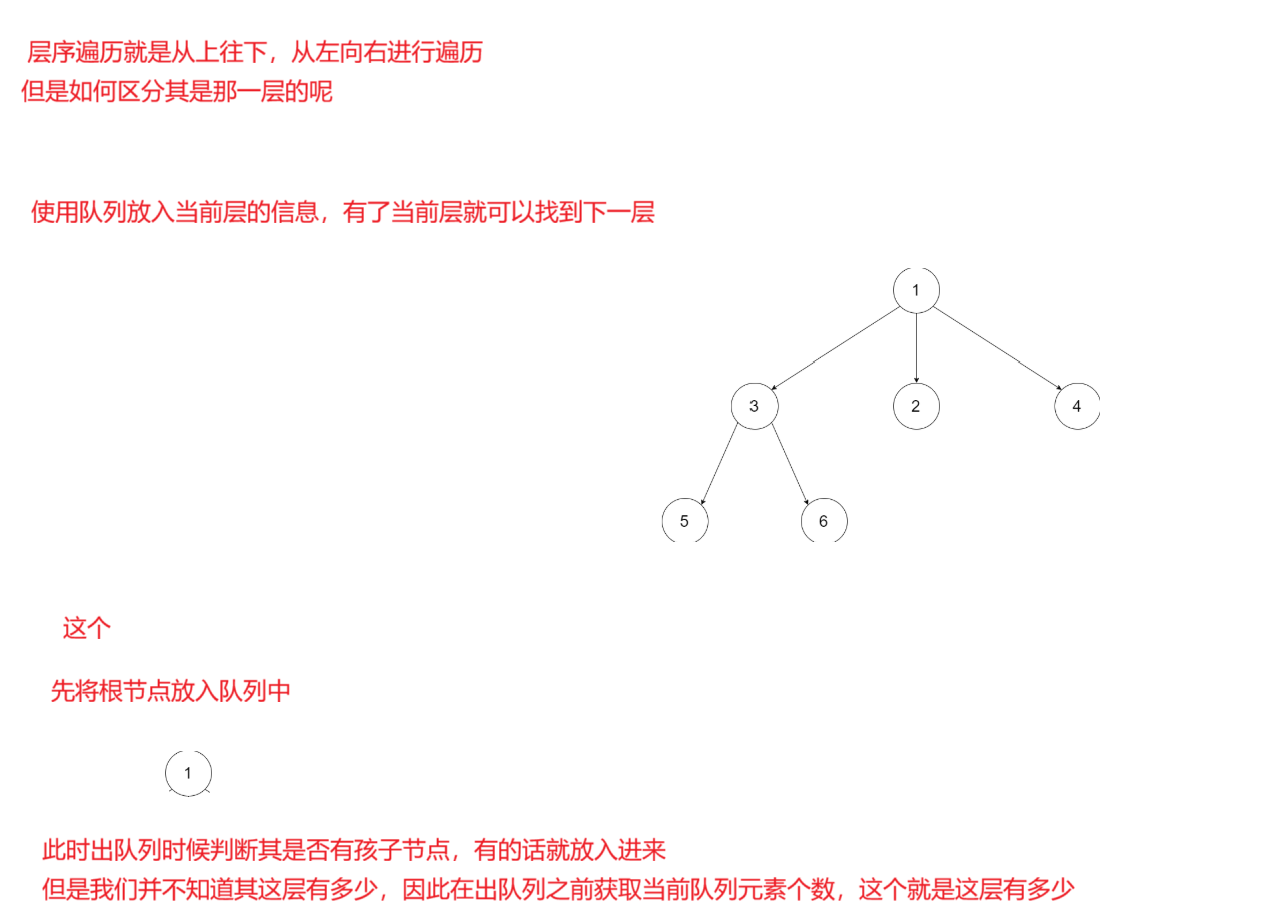

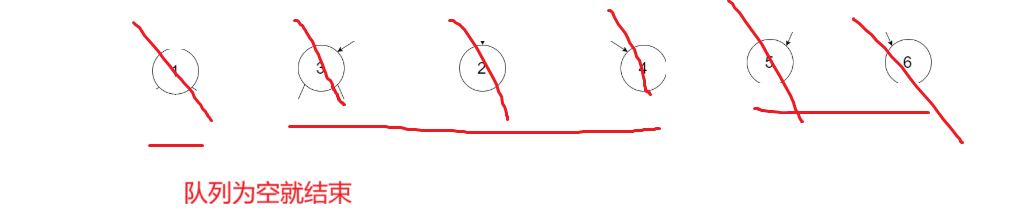
java
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<List<Integer>> levelOrder(Node root) {
//使用队列,每次出一层,出的过程中并判断其是否有海子节点
//如果有孩子节点,就将这个孩子按照从左到右的顺序放入栈中
Queue<Node> queue = new ArrayDeque<>();
List<List<Integer>> ret = new ArrayList<>();
//先将根节点放入
if (root == null) {
return ret;
}
queue.offer(root);
//不断出队列和入队列
while (!queue.isEmpty()) {
//看要出多少次
int n = queue.size();
List<Integer> tem = new ArrayList<>();
for (int i = 0; i < n; i++) {
//获取队头元素
Node cur = queue.poll();
tem.add(cur.val);
//判断其是否有儿子节点
for (Node child : cur.children) {
if (child != null) {
queue.offer(child);
}
}
}
ret.add(tem);
}
return ret;
}
}二叉树的锯齿形层序遍历
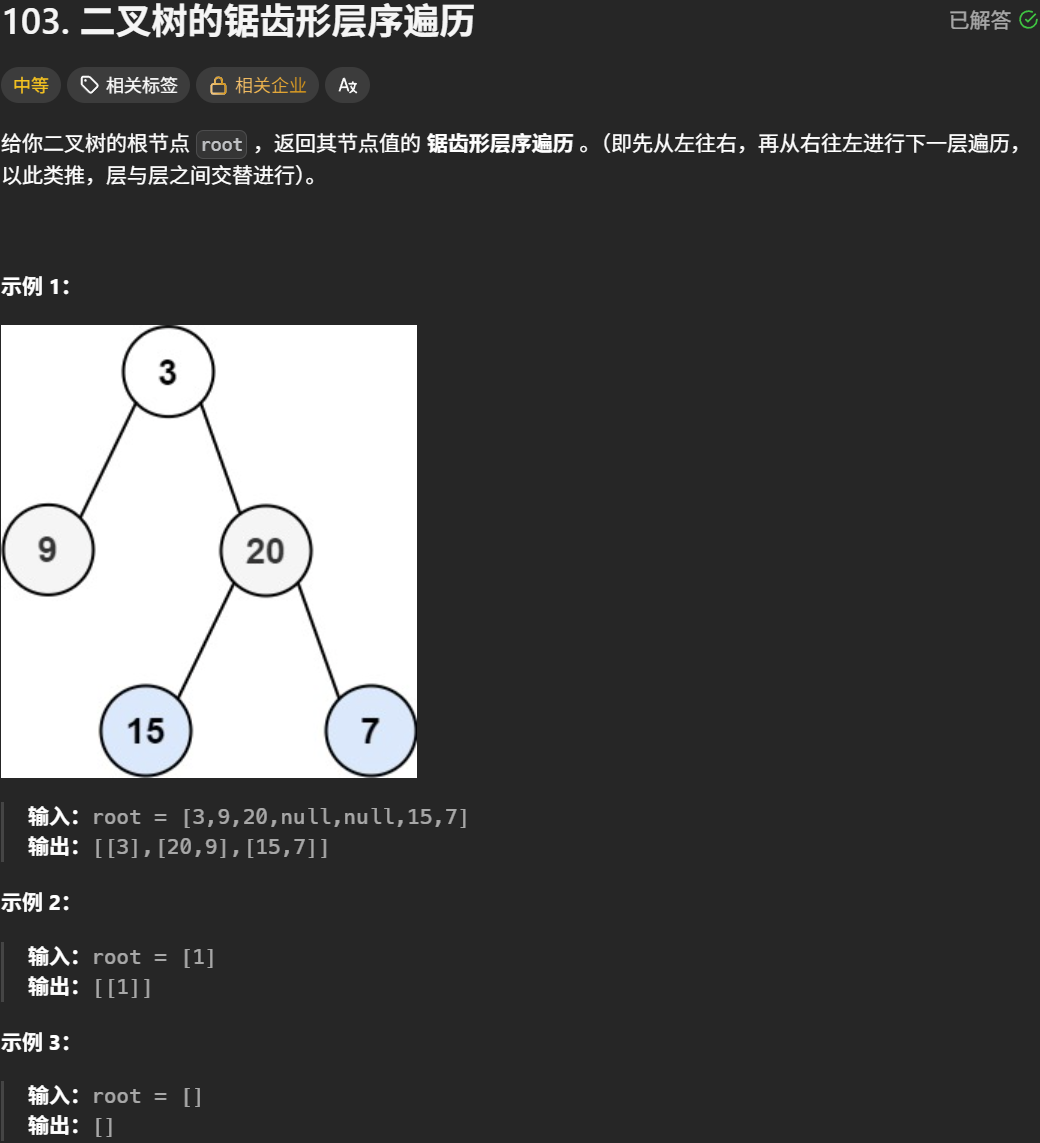
题目解析:和N叉树层序遍历类似,唯一区别就是它是从左向右,从右向左依次交替
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
//这里和层序遍历的区别就是,会从左往右,从右向左依次交替
List<List<Integer>> ret = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if (root == null) {
return ret;
}
//只需要一个标志位,标记一下反过来的,我们只需加入之后进行逆序即可
boolean flag = false;
queue.offer(root);
List<Integer> tem;
while (!queue.isEmpty()) {
int n = queue.size();
tem = new ArrayList<>();
for (int i = 0; i < n; i++) {
TreeNode cur = queue.poll();
tem.add(cur.val);
//判断是否有孩子
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
//判断是否要逆序,ture就是要逆序
if (flag == true) {
Collections.reverse(tem);
}
ret.add(tem);
flag = !flag;
}
return ret;
}
}在每个树行中找最大值

题目解析 :就是将每一行的最大值找出来
思想:像N叉树的层序遍历,我们只需要遍历过程中统计一下其每一行的最大值拼接到后面即可
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> largestValues(TreeNode root) {
//遍历层序过程并且找出这一层的最大值即可
List<Integer> ret = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root == null){
return ret;
}
queue.offer(root);
while(!queue.isEmpty()){
int n = queue.size();//这一层的数量
int max = Integer.MIN_VALUE;
for(int i = 0;i < n;i++){
TreeNode cur = queue.poll();
max = Math.max(max,cur.val);
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
ret.add(max);
}
return ret;
}
}二叉树最大宽度
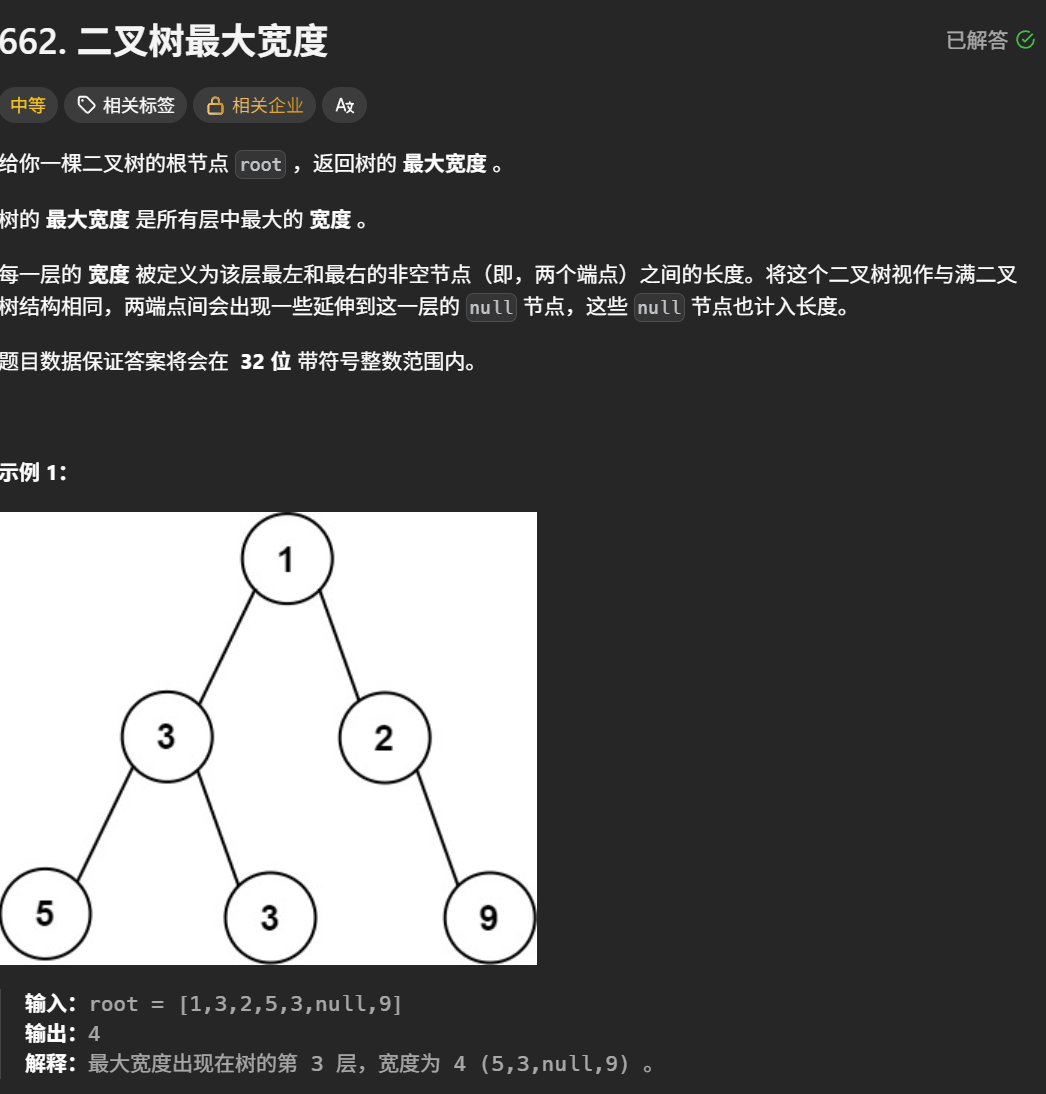
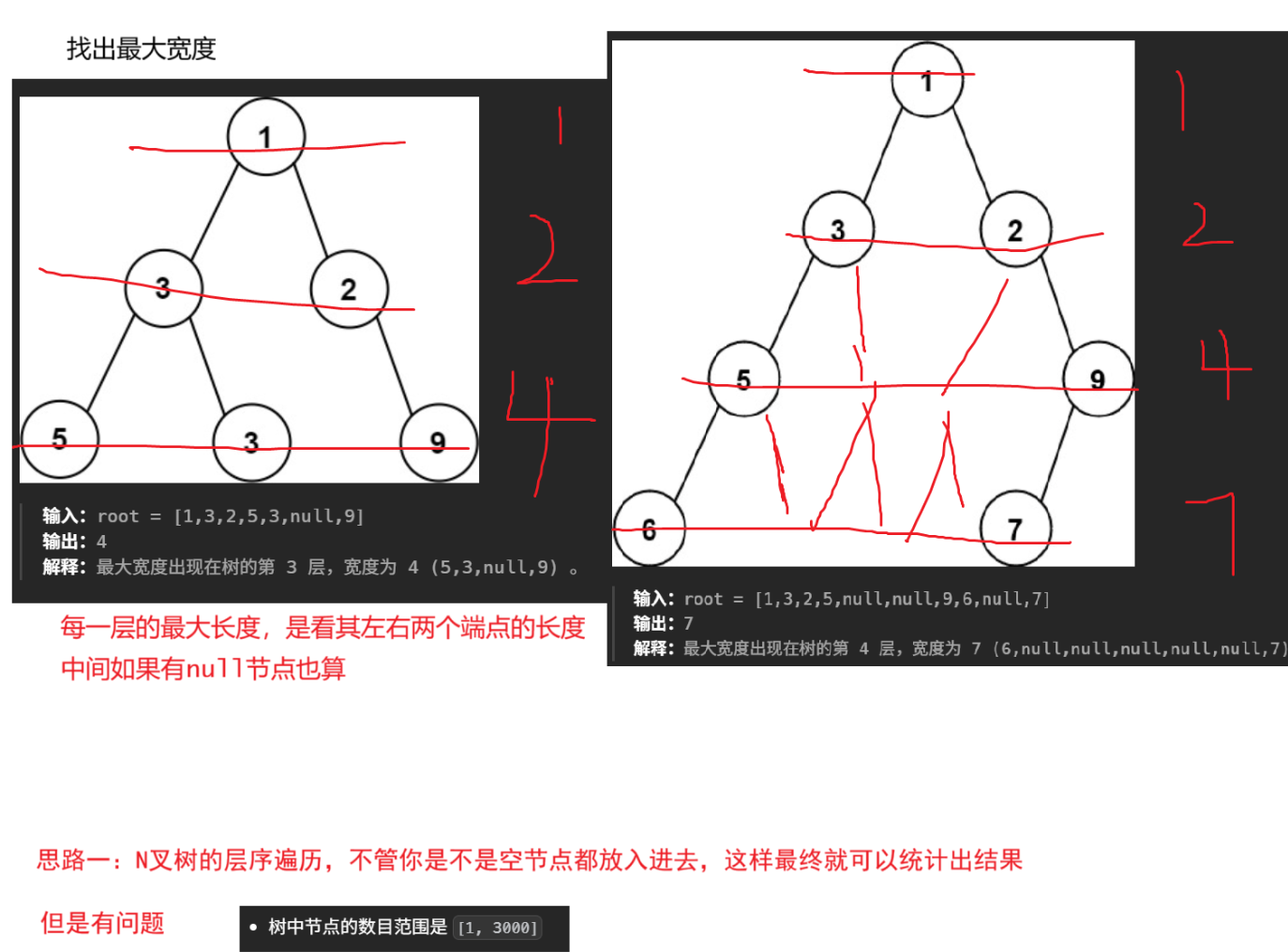
题目解析 :找出最大宽度,此时的宽度是每一层的最最左边和最右边之间长度,并且这里面会包括null空节点
利用二叉树下标性质,最终计算下标差值即可,这里采用数组模拟队列存放节点和下标对应关系
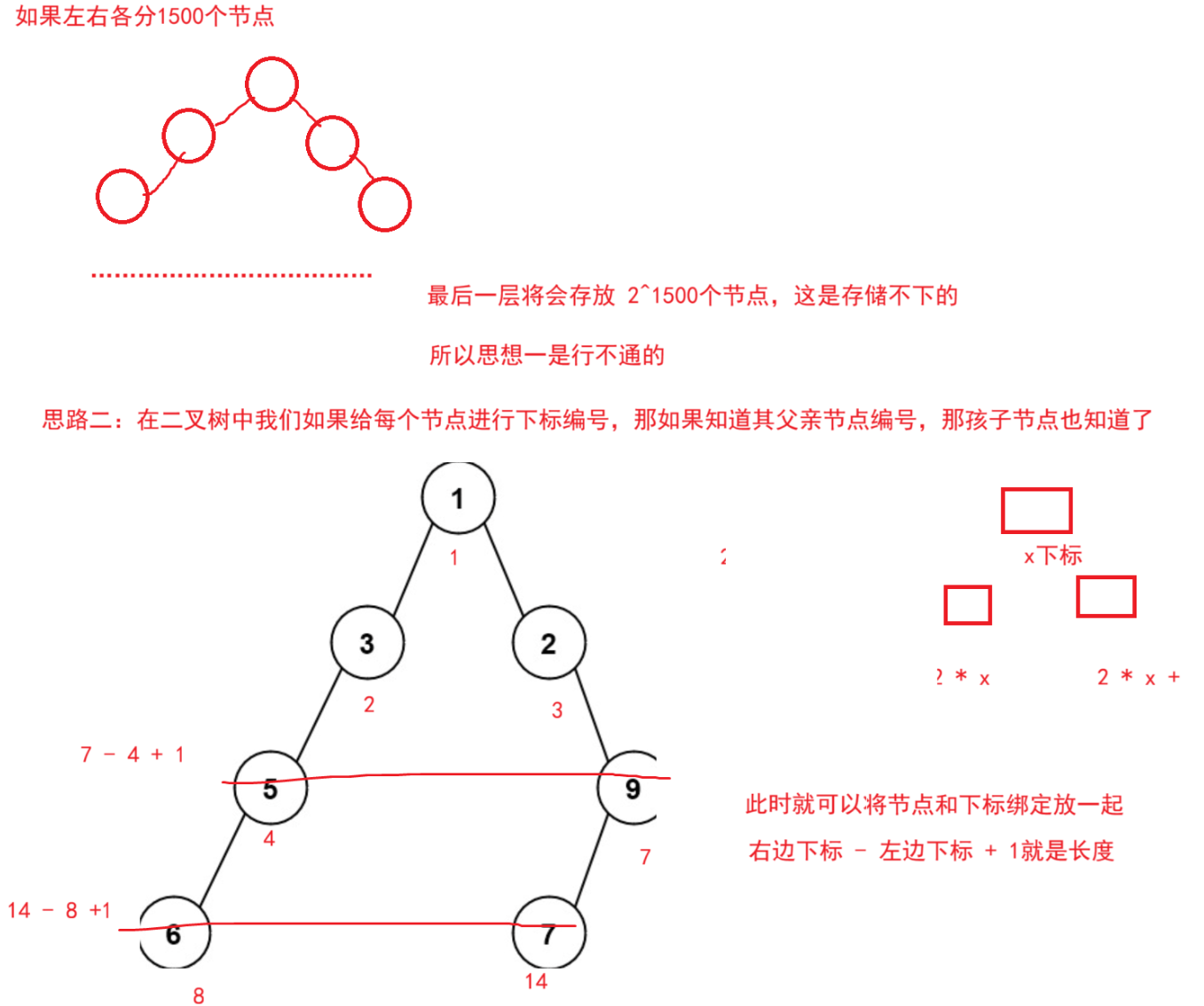

java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int widthOfBinaryTree(TreeNode root) {
//这里使用一个数组模拟队列
List<Pair<TreeNode,Integer>> queue = new ArrayList<>();
int ret = 0;//记录最大宽度
//先将根节点放入
queue.add(new Pair<TreeNode,Integer>(root,1));
//通过节点下标确定其最大宽度
while(!queue.isEmpty()){
//更新这一层的宽度
Pair<TreeNode,Integer> t1 = queue.get(0);
Pair<TreeNode,Integer> t2 = queue.get(queue.size()-1);
ret = Math.max(ret,t2.getValue() - t1.getValue() + 1);
//放下一层节点,根据其节点下标性质
//将这一层重新放一个新的数组中
List<Pair<TreeNode,Integer>> tem = new ArrayList<>();
for(Pair<TreeNode,Integer> q : queue){
TreeNode cur = q.getKey();//节点
int index = q.getValue();//下标
if(cur.left != null){
tem.add(new Pair<TreeNode,Integer>(cur.left,2*index));
}
if(cur.right != null){
tem.add(new Pair<TreeNode,Integer>(cur.right,2*index + 1));
}
}
queue = tem;//最新一层
}
return ret;
}
}