2025Cesium进阶教程（5）| webgis智慧城市开发，大屏可视化行政区高亮

2025cesium进阶教程持续更新中......

前篇：

Cesium进阶教程（1）customShader的使用

Cesium进阶教程（2）|基于 Cesium 后处理Post Processing的图形绘制

cesium进阶教程（3）发光流动线实例讲解，实现自定义 MaterialProperty

Cesium进阶（4）| 动态响应的发光流动线实例讲解

在政务决策、城市治理、应急响应这些实际工作里，GIS 大屏已经成了查看空间数据的常用工具。而行政区高亮这个功能，则能帮工作人员快速从复杂的地图信息里找到重点 。

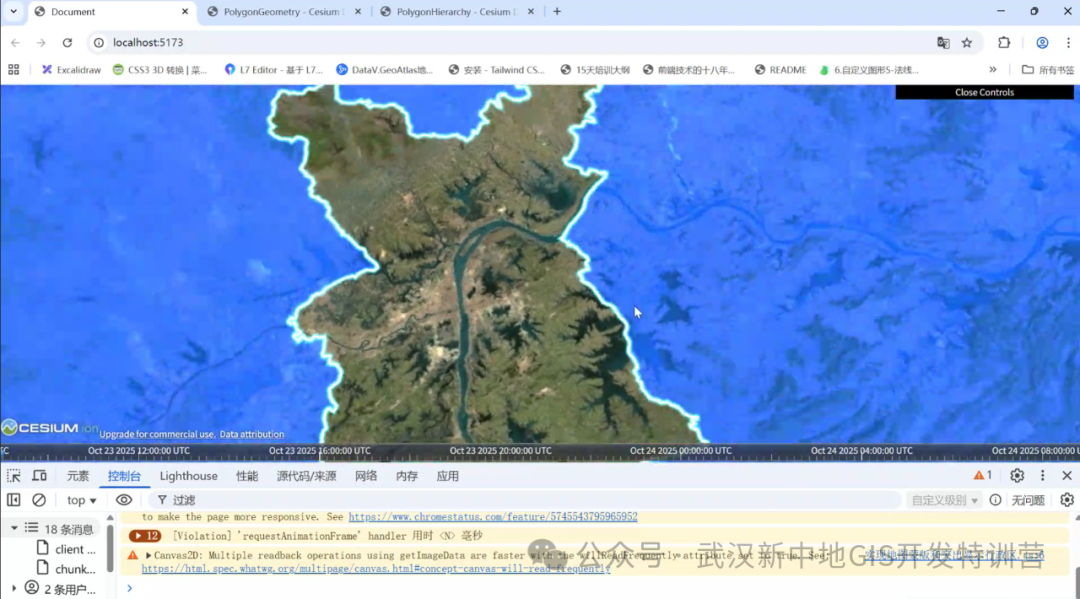
要让特定行政区在 Cesium 地图中 "凸显"，核心方法是 "地图蒙版 + 行政区挖孔"。简单说，就是先做一个覆盖全球的半透明蒙版，再把需要重点展示的行政区从蒙版里 "挖" 出来。这样一来，被挖空的行政区没有蒙版遮挡，自然就成了视觉焦点。

实现这一逻辑的关键技术依赖两个核心类：

• **PolygonGeometry：**用于创建多边形几何形状，是构建 "蒙版" 的基础；
• **PolygonHierarchy：**作为PolygonGeometry的polygonHierarchy属性参数，支持传入 "孔洞" 坐标数组 ------ 这正是 "挖孔" 功能的核心，只要把行政区的边界坐标传给PolygonHierarchy的第二个参数，就能在蒙版中挖去对应区域。

在创建全球蒙版的时候我们遇到了一个坑：

直接选择传入[ -180, 90, 180, 90, 180, -90, -180, -90]会发现没有效果。

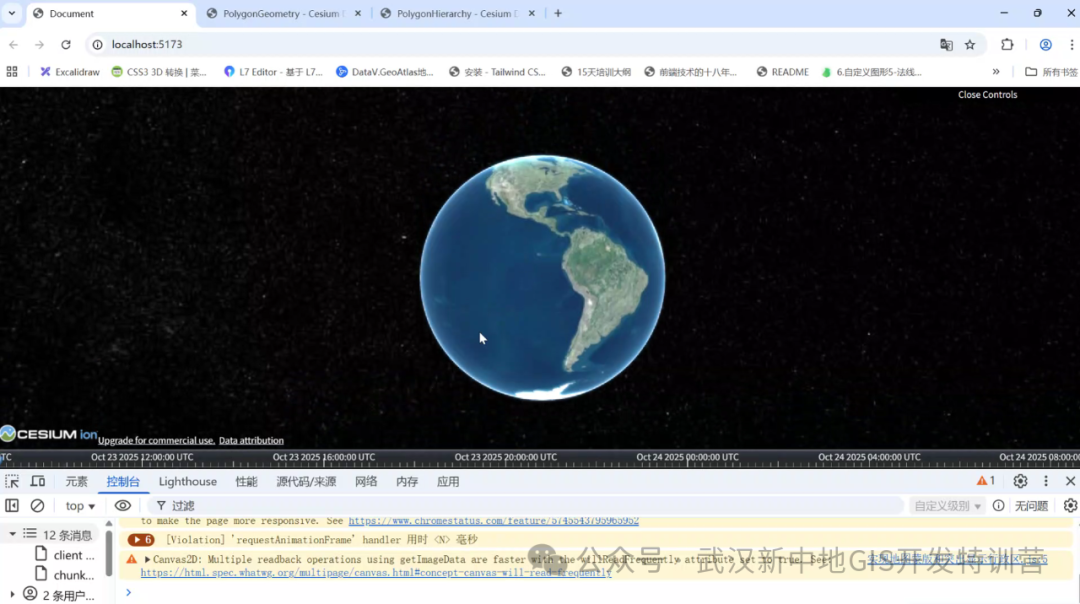
这是因为在cesium里面 实体放在地球上是一个曲面，指定的点实际上会有两个面，cesium会优先渲染小的那个面所以实际上我们传入的这些顶点在cesium里面刚好在一条线上所以不会渲染

那我们要怎么解决这个问题呢？

实际上也很简单，我们只需要分为东西两个半球然后渲染两个面就行了;

然后再根据情况选择在哪个面上挖孔.

以下是完整代码：

/**
 * 添加全球蒙版Primitive（分东西半球）
 * @param {Cesium.Viewer} viewer - Cesium Viewer实例
 */
function addPrimitive(viewer) {  
  // 1. 定义西半球坐标（经度：-180°~-0.00001°，纬度：-60°~60°）
  // 注：纬度用-60°~60°而非-90°~90°，后续会解析极区自动补全原理
  let wPositions = Cesium.Cartesian3.fromDegreesArray([  
    -0.00001, 60,    // 西半球东边界（接近0°），北纬60°
    -0.00001, -60,   // 西半球东边界，南纬60°
    -180, -60,       // 西半球西边界（180°W），南纬60°
    -180, 60,        // 西半球西边界，北纬60°
    -0.00001, 60,    // 闭合点，与第一个点一致
  ]);  
  // 2. 定义东半球坐标（经度：0.00001°~180°，纬度：-60°~60°）
  const ePositions = Cesium.Cartesian3.fromDegreesArray([  
    0.00001, 60,     // 东半球西边界（接近0°），北纬60°
    0.00001, -60,    // 东半球西边界，南纬60°
    180, -60,        // 东半球东边界（180°E），南纬60°
    180, 60,         // 东半球东边界，北纬60°
    0.00001, 60,     // 闭合点，与第一个点一致
  ]);  
  // 3. 创建西半球PolygonGeometry（核心：指定arcType为GEODESIC）
  const wGeometry = new Cesium.PolygonGeometry({  
    polygonHierarchy: new Cesium.PolygonHierarchy(wPositions),  // 多边形层级（含边界）
    arcType: Cesium.ArcType.GEODESIC,  // 球面插值（大圆弧线），关键参数
  });  
  // 4. 创建西半球GeometryInstance（几何实例，用于批量渲染）
  const wInstance = new Cesium.GeometryInstance({  
    geometry: wGeometry,  // 绑定西半球几何
  });  
  // 5. 创建东半球PolygonGeometry（与西半球逻辑一致）
  const eGeometry = new Cesium.PolygonGeometry({  
    polygonHierarchy: new Cesium.PolygonHierarchy(ePositions),  
    arcType: Cesium.ArcType.GEODESIC,  
  });  
  // 6. 创建东半球GeometryInstance
  const eInstance = new Cesium.GeometryInstance({  
    geometry: eGeometry,  
  });
  // 7. 定义蒙版材质（半透明红色，alpha=0.5）
  const material = new Cesium.Material({  
    fabric: {  
      type: "Color",  // 颜色材质类型
      uniforms: {  
        color: Cesium.Color.RED.withAlpha(0.5),  // 半透明红色
      },  
    },  
  });  
  // 8. 定义材质外观（绑定材质）
  const appearance = new Cesium.MaterialAppearance({  
    material: material,  // 绑定半透明材质
  });  
  // 9. 创建GroundPrimitive（贴地渲染的图元）
  const primitive = new Cesium.GroundPrimitive({  
    geometryInstances: [wInstance, eInstance],  // 同时渲染东西半球
    appearance: appearance,  // 绑定外观
  });  
  // 10. 将蒙版添加到场景中
  viewer.scene.primitives.add(primitive);
}

可以看到，我们的纬度范围并不是-90到90 而是-60-60 那为什么也可以覆盖全球呢？

这是因为我们选的arcType为GEODESIC。 这其实正是Cesium 世界坐标系统的几何映射边界 与 球面经纬投影连续性 的核心点。 用纬度范围 -60° ~ 60° 就能"看起来覆盖全球"，并不是巧合，而是因为 在 WGS84 椭球体上，PolygonGeometry 的球面插值和地球投影特性共同导致了"极区自动补全"。 我们分层来讲👇

0 1、Cesium 的经纬坐标系统简述

Cesium 使用 WGS84 椭球体（Earth 模型），经度范围 [-180°, +180°]，纬度范围 [-90°, +90°]。

● 经度（longitude）控制 东西方向；

● 纬度（latitude）控制 南北方向。

0 2、PolygonGeometry 的插值原理：

球面插值 + 投影特性

Cesium.PolygonGeometry 在构建时，默认会进行 球面插值 (ArcType.GEODESIC)。

这意味着：

• 它不是在平面上连线，而是在 地球表面沿大圆弧线 连线。

• 当你指定的纬度范围是 -60° ~ 60°，但跨越了整个经度范围（-180°~180°），

  实际在地球上构成了一个几乎包裹整个地球的球带。

而因为地球在极区是收缩的（经线收敛），所以当你画出从 -180° 到 180° 的闭合多边形时：

• 经纬线在 ±90° 的地方会自动"闭合"

• Cesium 的多边形三角剖分算法会把缺口（±60° 到 ±90°）补成一个封闭的面

这就造成了你看到的"好像覆盖整个地球"的效果。

0 3、关键细节：为什么不是只盖 ±60°？

Cesium 内部会在构造多边形时进行如下过程：

1. 将地理坐标投影到球面；

2. 使用球面三角剖分算法（PolygonPipeline.computeSubdivision）；

3. 若多边形跨越 ±180° 经线，它会被认为是一个"封闭带区"；

4. 由于三角剖分时使用了球面顶点法线（基于椭球表面插值），

   缺少极区顶点的地方，会被自动用三角面闭合补齐。

换句话说，当你画的多边形经度跨满 360° 时，
不论纬度多小，Cesium 都会把它当作"包裹整个球体的封闭面"。

0 4、验证

试着只改一行：

-0.00001, 30, -0.00001, -30, -180, -30, -180, 30

再看效果，你会发现：

地球依旧被一个半透明"壳"包着。

这说明它确实不是在纬度 30° 范围内画了个矩形，而是整球闭合。

其实还有一个arcType， RHUMB

1️⃣ GEODESIC（大圆弧线）

• 在球体上最短路径。

• 飞机航线、卫星轨迹常用这种路线。

• 连接地球上两点时，曲线通常会弯向极区。

• 在地图（墨卡托投影）上看是弯曲的线。

举例

连接北京（116°E, 40°N）到纽约（-74°E, 40°N）：

• GEODESIC 会从中国 → 北极圈上空 → 加拿大 → 美国东岸，明显向北拱起。

• 实际飞行路径就是这种。

2️⃣ RHUMB（恒向线）

• 保持恒定的航向角（compass bearing）。

• 适合船舶或某些传统导航用途。

• 在墨卡托投影地图上是一条直线。

• 但在地球表面上，它比大圆弧更长。

举例

同样连接北京到纽约的路线：

• RHUMB 会沿着接近恒定航向从西北方向横穿太平洋；

• 路线更长，不走极区。

二者数学差异

|-------------|--------------|---------------------|
| 项目 | GEODESIC | RHUMB |
| 定义方式 | 球面测地线 | 保持恒定航向角 |
| 曲线方程 | 解球面余弦定理（非线性） | 线性变化的经度与等角纬度 |
| 距离 | 最短路径 | 比大圆路径更长 |
| 投影表现 | 弯曲线 | 直线（在墨卡托投影下） |
| 数值特性 | 需球面三角计算 | 基于等角函数（tan(φ) ）计算 |
| Cesium 插值实现 | 球面插值（沿椭球） | 等角线插值（墨卡托系） |

Cesium 中的区别

在 Cesium 中，很多 Geometry（如 PolylineGeometry, PolygonGeometry）都可以指定：

arcType: Cesium.ArcType.GEODESIC   // 默认
// 或
arcType: Cesium.ArcType.RHUMB

GEODESIC

• Cesium 会在椭球面上插值点，使路径沿着大圆弧线。

• 适合飞行轨迹、地球表面等距线、球面过渡动画。

• 性能稳定，对跨越 ±180° 经线和极区都支持良好。

RHUMB

• Cesium 在等角（Mercator）投影空间进行线性插值。

• 适合航海航线、地图导航轨迹。

• 但在接近极点、跨 ±180° 经线时可能数值不稳定。

实际可视化上的区别（在地球上 vs 在平面地图）

所以回到我们之前的那个问题

ArcType.GEODESIC 代表沿椭球面的最短路径插值。

当 Cesium 看到一条从 -180° 到 +180° 的边时，它认为两者相距：

Δλ = 180° - (-180°) = 360°

但根据最短路径原则，Cesium 实际上会取 最短方向，即：

"360° 反向的 0° 差值"

也就是说，Cesium 认为：

-180° ≈ +180° （它们是同一个点）

于是这四个顶点被理解成：

[-180,90] ≈ [180,90]
[-180,-90] ≈ [180,-90]

结果整个多边形在球面上变成了一条零宽度的经线面（实际上面积为0）。

看不明白没关系，点这里可以查看视频解析👇

5.cesium进阶实战教程：覆盖全球的蒙版效果突出显示行政区_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1yrs1zEE79?vd_source=8c32bbccf29164719fe4e4c40c768444&p=5&spm_id_from=333.788.videopod.episodes